小白也能看懂的 ROC 曲線詳解
↓推薦關(guān)注↓
ROC 曲線是一種坐標(biāo)圖式的分析工具,是由二戰(zhàn)中的電子和雷達(dá)工程師發(fā)明的,發(fā)明之初是用來偵測(cè)敵軍飛機(jī)、船艦,后來被應(yīng)用于醫(yī)學(xué)、生物學(xué)、犯罪心理學(xué)。
如今,ROC 曲線已經(jīng)被廣泛應(yīng)用于機(jī)器學(xué)習(xí)領(lǐng)域的模型評(píng)估,說到這里就不得不提到 Tom Fawcett 大佬,他一直在致力于推廣 ROC 在機(jī)器學(xué)習(xí)領(lǐng)域的應(yīng)用,他發(fā)布的論文《An introduction to ROC analysis》[1]更是被奉為 ROC 的經(jīng)典之作(引用 2.2w 次),知名機(jī)器學(xué)習(xí)庫(kù) scikit-learn 中的 ROC 算法就是參考此論文實(shí)現(xiàn),可見其影響力!
不知道大多數(shù)人是否和我一樣,對(duì)于 ROC 曲線的理解只停留在調(diào)用 scikit-learn 庫(kù)的函數(shù),對(duì)于它的背后原理和公式所知甚少。
前幾天我重讀了《An introduction to ROC analysis》終于將 ROC 曲線徹底搞清楚了,獨(dú)樂樂不如眾樂樂!如果你也對(duì) ROC 的算法及實(shí)現(xiàn)感興趣,不妨花些時(shí)間看完全文,相信你一定會(huì)有所收獲!推薦關(guān)注@公眾號(hào):數(shù)據(jù)STUDIO 更多優(yōu)質(zhì)好文~
一、什么是 ROC 曲線
下圖中的藍(lán)色曲線就是 ROC 曲線,它常被用來評(píng)價(jià)二值分類器的優(yōu)劣,即評(píng)估模型預(yù)測(cè)的準(zhǔn)確度。
二值分類器,就是字面意思它會(huì)將數(shù)據(jù)分成兩個(gè)類別(正/負(fù)樣本)。例如:預(yù)測(cè)銀行用戶是否會(huì)違約、內(nèi)容分為違規(guī)和不違規(guī),以及廣告過濾、圖片分類等場(chǎng)景。篇幅關(guān)系這里不做多分類 ROC 的講解。

坐標(biāo)系中縱軸為 TPR(真陽(yáng)率/命中率/召回率)最大值為 1,橫軸為 FPR(假陽(yáng)率/誤判率)最大值為 1,虛線為基準(zhǔn)線(最低標(biāo)準(zhǔn)),藍(lán)色的曲線就是 ROC 曲線。其中 ROC 曲線距離基準(zhǔn)線越遠(yuǎn),則說明該模型的預(yù)測(cè)效果越好。(TPR: True positive rate; FPR: False positive rate)
-
ROC 曲線接近左上角:模型預(yù)測(cè)準(zhǔn)確率很高 -
ROC 曲線略高于基準(zhǔn)線:模型預(yù)測(cè)準(zhǔn)確率一般 -
ROC 低于基準(zhǔn)線:模型未達(dá)到最低標(biāo)準(zhǔn),無法使用
二、背景知識(shí)
考慮一個(gè)二分類模型, 負(fù)樣本(Negative) 為 0,正樣本(Positive) 為 1。即:
-
標(biāo)簽 $y$ 的取值為 0 或 1。 -
模型預(yù)測(cè)的標(biāo)簽為 $\hat{y}$,取值也是 0 或 1。
因此,將 $y$ 與 $\hat{y}$ 兩兩組合就會(huì)得到 4 種可能性,分別稱為:
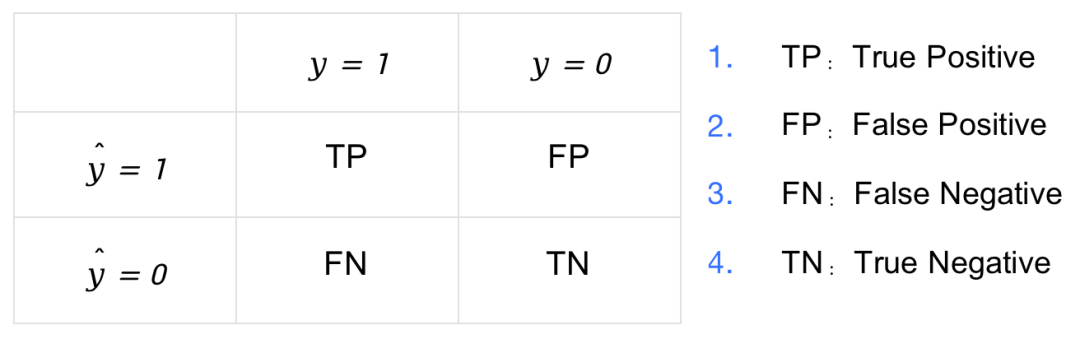
2.1 公式
ROC 曲線的橫坐標(biāo)為 FPR(False Positive Rate),縱坐標(biāo)為 TPR(True Positive Rate)。FPR 統(tǒng)計(jì)了所有負(fù)樣本中 預(yù)測(cè)錯(cuò)誤(FP) 的比例,TPR 統(tǒng)計(jì)了所有正樣本中 預(yù)測(cè)正確(TP) 的比例,其計(jì)算公式如下,其中 # 表示統(tǒng)計(jì)個(gè)數(shù),例如 #N 表示負(fù)樣本的個(gè)數(shù),#P 表示正樣本的個(gè)數(shù)
$$\text{FPR}=\frac{\#\text{FP}}{\#\text{N}} $$ $$\text{TPR}=\frac{\#\text{TP}}{\#\text{P}} $$2.2 計(jì)算方法
下面舉一個(gè)實(shí)際例子作為講解,以下表 5 個(gè)樣本為例,講解如何計(jì)算 FPR 和 TPR。
| id | 真實(shí)標(biāo)簽 $y$ | 預(yù)測(cè)標(biāo)簽 $\hat{y}$ |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 0 |
| 3 | 0 | 0 |
| 4 | 1 | 1 |
| 5 | 0 | 1 |
正樣本數(shù) $\#P=3$,負(fù)樣本數(shù) $\#N=2$。
其中 $y=0$ 且 $\hat{y}=1$ 的樣本有 1 個(gè),即 $\#FP=1$,所以 $FPR=1/2=0.5$
其中 $y=1$ 且 $\hat{y}=1$ 的樣本有 2 個(gè),即 $\#TP=2$,所以 $FPR=2/3$
FPR 和 TPR 的取值范圍均是 0 到 1 之間。對(duì)于 FPR,我們希望其越小越好。而對(duì)于 TPR,我們希望其越大越好。
至此,我們已經(jīng)介紹完如何計(jì)算 FPR 和 TPR 的值,下面將會(huì)講解如何繪制 ROC 曲線。
三、繪制 ROC 曲線
講到這里,可能有的同學(xué)會(huì)問:ROC 不是一條曲線嗎?講了這么多它到底應(yīng)該怎么畫呢?下面將分為兩部分講解如何繪制 ROC 曲線,直接打通你的“任督二脈”徹底拿下 ROC 曲線:
-
第一部分:通過手繪的方式講解原理 -
第二部分:Python 代碼實(shí)現(xiàn),代碼清爽易讀
如果說上面是“開胃小菜”,那下面就是正菜啦!
3.1 手繪 ROC 曲線
一般在二分類模型里(標(biāo)簽取值為 0 或 1),會(huì)默認(rèn)設(shè)定一個(gè)閾值 (threshold)。當(dāng)預(yù)測(cè)分?jǐn)?shù)大于這個(gè)閾值時(shí),輸出 1,反之輸出 0。我們可以通過調(diào)節(jié)這個(gè)閾值,改變模型預(yù)測(cè)的輸出,進(jìn)而畫出 ROC 曲線。
以下面表格中的 20 個(gè)點(diǎn)為例,介紹如何人工畫出 ROC 曲線,其中正樣本和負(fù)樣本都是 10 個(gè),即 $\#P = \#N = 10$。
| id | 真實(shí)標(biāo)簽 | 預(yù)測(cè)分?jǐn)?shù) | id | 真實(shí)標(biāo)簽 | 預(yù)測(cè)分?jǐn)?shù) |
|---|---|---|---|---|---|
| 1 | 1 | .9 | 11 | 1 | .4 |
| 2 | 1 | .8 | 12 | 0 | .39 |
| 3 | 0 | .7 | 13 | 1 | .38 |
| 4 | 1 | .6 | 14 | 0 | .37 |
| 5 | 1 | .55 | 15 | 0 | .36 |
| 6 | 1 | .54 | 16 | 0 | .35 |
| 7 | 0 | .53 | 17 | 1 | .34 |
| 8 | 0 | .52 | 18 | 0 | .33 |
| 9 | 1 | .51 | 19 | 1 | .30 |
| 10 | 0 | .505 | 20 | 0 | .1 |
當(dāng)設(shè)定閾值為 0.9 時(shí),只有第一個(gè)點(diǎn)預(yù)測(cè)為 1,其余都為 0,故 $\#FP=0$、$\#TP=1$,計(jì)算出 $FPR=0/10=0$,$TPR=1/10=0.1$,畫出點(diǎn) (0,0.1)
當(dāng)設(shè)定閾值為 0.8 時(shí),只有前兩個(gè)點(diǎn)預(yù)測(cè)為 1,其余都為 0,故 $\#FP=0、\#TP=2$,計(jì)算出 $FPR=0/10=0,TPR=2/10=0.2$,畫出點(diǎn) (0,0.2)
當(dāng)設(shè)定閾值為 0.7 時(shí),只有前三個(gè)點(diǎn)預(yù)測(cè)為 1,其余都為 0,故 $\#FP=1、\#TP=2$,計(jì)算出 $FPR=1/10=0.1,TPR=2/10=0.2$,畫出點(diǎn) (0.1,0.2)。
以此類推,畫出的 ROC 曲線如下:
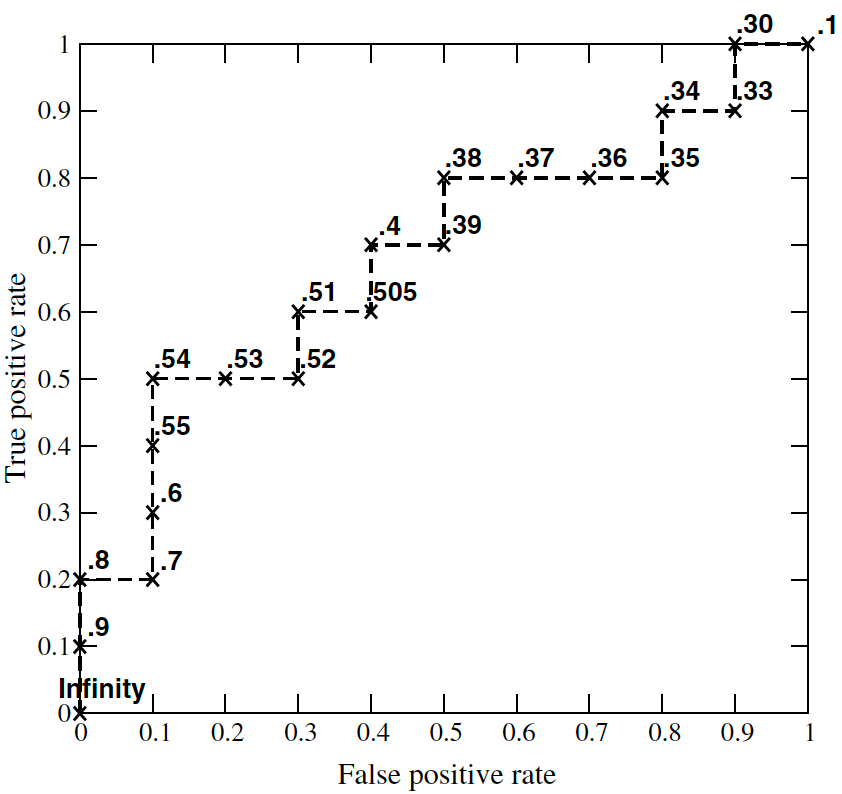
因此,在畫 ROC 曲線前,需要將預(yù)測(cè)分?jǐn)?shù)從大到小排序,然后將預(yù)測(cè)分?jǐn)?shù)依次設(shè)定為閾值,分別計(jì)算 $FPR$ 和 $TPR$。而對(duì)于基準(zhǔn)線,假設(shè)隨機(jī)預(yù)測(cè)為正樣本的概率為 $x$,即 $\Pr(\hat{y}=1)=x$ 由于 $FPR$ 計(jì)算的是負(fù)樣本中,預(yù)測(cè)為正樣本的概率,因此 FPR= $x$(同理,TPR= $x$)。所以,基準(zhǔn)線為從點(diǎn) (0, 0) 到 (1, 1) 的斜線。
3.2 Python 代碼
接下來,我們將結(jié)合代碼講解如何在 Python 中繪制 ROC 曲線。
下面的代碼參考了《An Introduction to ROC Analysis》[2]中的算法 1(偽代碼)。值得一提的是,知名機(jī)器學(xué)習(xí)庫(kù) scikit-learn 的 roc_curve 函數(shù)[3] 也參考了這個(gè)算法。

下面我自己實(shí)現(xiàn)的 roc 函數(shù)可以理解為是簡(jiǎn)化版的 roc_curve,這里的代碼邏輯更加簡(jiǎn)潔易懂,算法的時(shí)間復(fù)雜度 O ( n log ? n ) O(n\log n) O(nlogn)。推薦關(guān)注@公眾號(hào):數(shù)據(jù)STUDIO 更多優(yōu)質(zhì)好文~
完整的代碼如下:
# import numpy as np
def roc(y_true, y_score, pos_label):
"""
y_true:真實(shí)標(biāo)簽
y_score:模型預(yù)測(cè)分?jǐn)?shù)
pos_label:正樣本標(biāo)簽,如“1”
"""
# 統(tǒng)計(jì)正樣本和負(fù)樣本的個(gè)數(shù)
num_positive_examples = (y_true == pos_label).sum()
num_negtive_examples = len(y_true) - num_positive_examples
tp, fp = 0, 0
tpr, fpr, thresholds = [], [], []
score = max(y_score) + 1
# 根據(jù)排序后的預(yù)測(cè)分?jǐn)?shù)分別計(jì)算fpr和tpr
for i in np.flip(np.argsort(y_score)):
# 處理樣本預(yù)測(cè)分?jǐn)?shù)相同的情況
if y_score[i] != score:
fpr.append(fp / num_negtive_examples)
tpr.append(tp / num_positive_examples)
thresholds.append(score)
score = y_score[i]
if y_true[i] == pos_label:
tp += 1
else:
fp += 1
fpr.append(fp / num_negtive_examples)
tpr.append(tp / num_positive_examples)
thresholds.append(score)
return fpr, tpr, thresholds
導(dǎo)入上面 3.1 表格中的數(shù)據(jù),通過上面實(shí)現(xiàn)的 roc 方法,計(jì)算 ROC 曲線的坐標(biāo)值。
import numpy as np
y_true = np.array(
[1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0]
)
y_score = np.array([
.9, .8, .7, .6, .55, .54, .53, .52, .51, .505,
.4, .39, .38, .37, .36, .35, .34, .33, .3, .1
])
fpr, tpr, thresholds = roc(y_true, y_score, pos_label=1)
最后,通過 Matplotlib 將計(jì)算出的 ROC 曲線坐標(biāo)繪制成圖。
import matplotlib.pyplot as plt
plt.plot(fpr, tpr)
plt.axis("square")
plt.xlabel("False positive rate")
plt.ylabel("True positive rate")
plt.title("ROC curve")
plt.show()
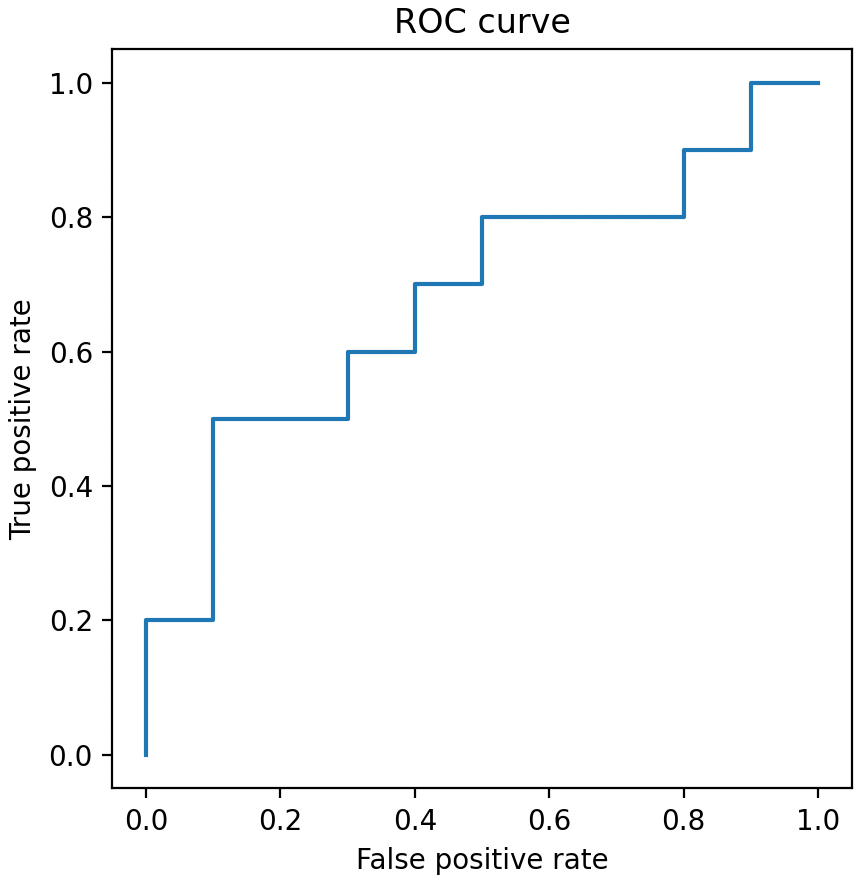
至此,ROC 的基礎(chǔ)知識(shí)部分就全部講完了,如果還想深入了解的同學(xué)可以繼續(xù)往下看。
四、聯(lián)邦學(xué)習(xí)中的 ROC 平均
如果將上面的內(nèi)容比作“正餐”,那這里就是妥妥干貨了,打起精神沖鴨!
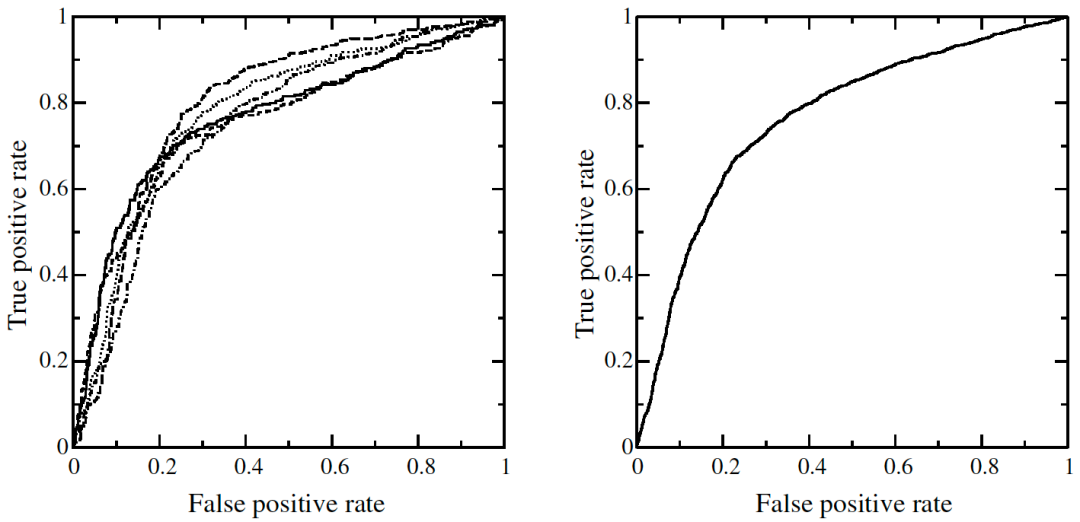
顧名思義,ROC 平均就是將多條 ROC 曲線“平均化”。那么,什么場(chǎng)景需要做 ROC 平均呢?例如:橫向聯(lián)邦學(xué)習(xí)中,由于樣本都在用戶本地,服務(wù)器可以采用 ROC 平均的方式,計(jì)算近似的全局 ROC 曲線。
ROC 的平均有兩種方法:垂直平均、閾值平均,下面將逐一進(jìn)行講解,并給出 Python 代碼實(shí)現(xiàn)。
4.1 垂直平均
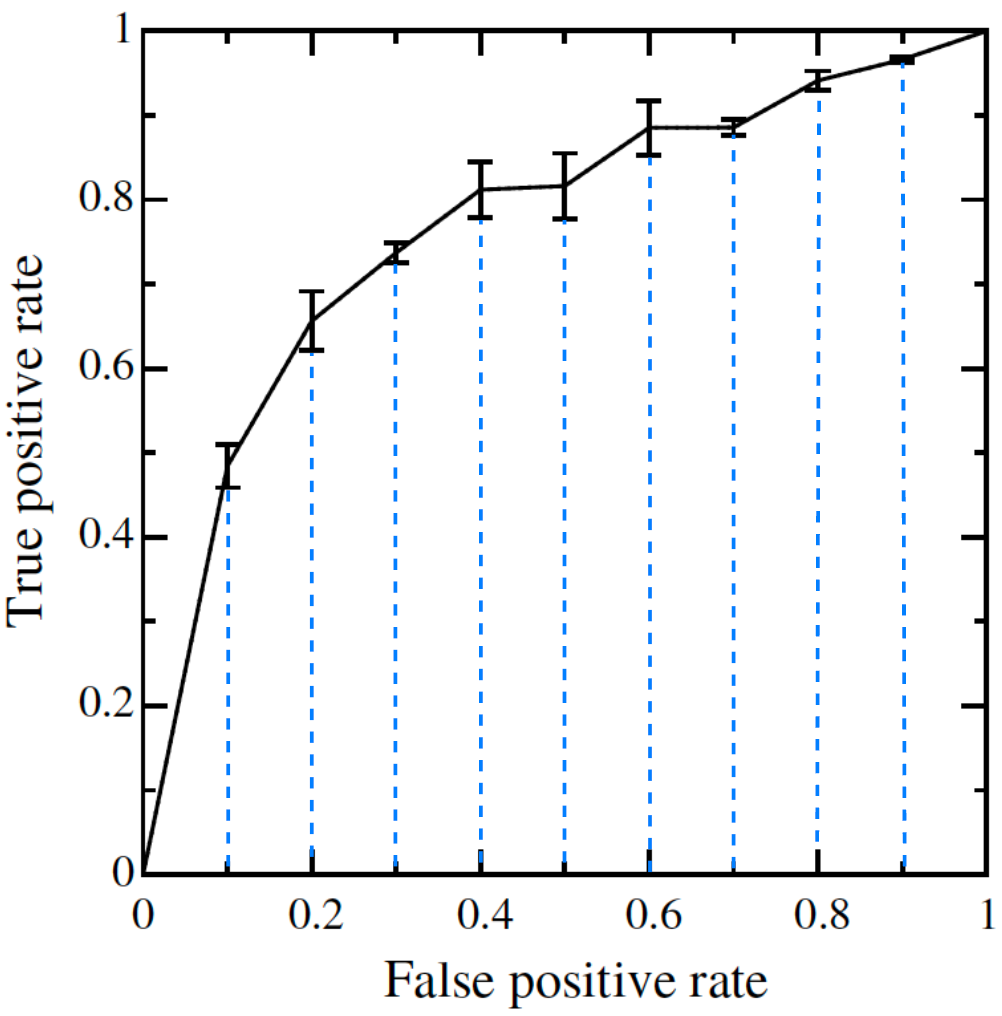
垂直平均(Vertical averaging)的思想是,選取一些 FPR 的點(diǎn),計(jì)算其平均的 TPR 值。下面是論文中的算法描述的偽代碼,看不懂可直接略過看 Python 代碼實(shí)現(xiàn)部分。

下面是 Python 的代碼實(shí)現(xiàn):
# import numpy as np
def roc_vertical_avg(samples, FPR, TPR):
"""
samples:選取FPR點(diǎn)的個(gè)數(shù)
FPR:包含所有FPR的列表
TPR:包含所有TPR的列表
"""
nrocs = len(FPR)
tpravg = []
fpr = [i / samples for i in range(samples + 1)]
for fpr_sample in fpr:
tprsum = 0
# 將所有計(jì)算的tpr累加
for i in range(nrocs):
tprsum += tpr_for_fpr(fpr_sample, FPR[i], TPR[i])
# 計(jì)算平均的tpr
tpravg.append(tprsum / nrocs)
return fpr, tpravg
# 計(jì)算對(duì)應(yīng)fpr的tpr
def tpr_for_fpr(fpr_sample, fpr, tpr):
i = 0
while i < len(fpr) - 1 and fpr[i + 1] <= fpr_sample:
i += 1
if fpr[i] == fpr_sample:
return tpr[i]
else:
return interpolate(fpr[i], tpr[i], fpr[i + 1], tpr[i + 1], fpr_sample)
# 插值
def interpolate(fprp1, tprp1, fprp2, tprp2, x):
slope = (tprp2 - tprp1) / (fprp2 - fprp1)
return tprp1 + slope * (x - fprp1)
4.2 閾值平均
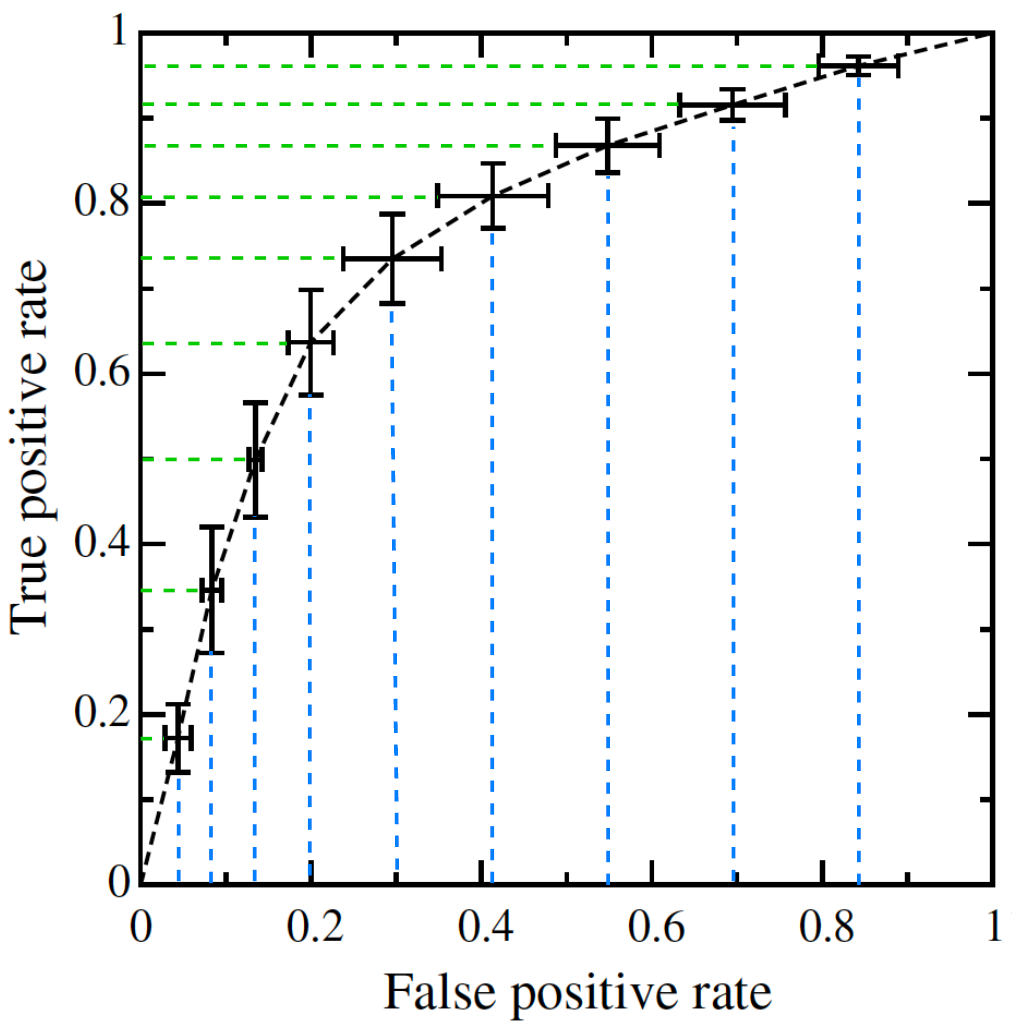
閾值平均(Threshold averaging)的思想是,選取一些閾值的點(diǎn),計(jì)算其平均的 FPR 和 TPR。

下面是 Python 的代碼實(shí)現(xiàn):
# import numpy as np
def roc_threshold_avg(samples, FPR, TPR, THRESHOLDS):
"""
samples:選取FPR點(diǎn)的個(gè)數(shù)
FPR:包含所有FPR的列表
TPR:包含所有TPR的列表
THRESHOLDS:包含所有THRESHOLDS的列表
"""
nrocs = len(FPR)
T = []
fpravg = []
tpravg = []
for thresholds in THRESHOLDS:
for t in thresholds:
T.append(t)
T.sort(reverse=True)
for tidx in range(0, len(T), int(len(T) / samples)):
fprsum = 0
tprsum = 0
# 將所有計(jì)算的fpr和tpr累加
for i in range(nrocs):
fprp, tprp = roc_point_at_threshold(FPR[i], TPR[i], THRESHOLDS[i], T[tidx])
fprsum += fprp
tprsum += tprp
# 計(jì)算平均的fpr和tpr
fpravg.append(fprsum / nrocs)
tpravg.append(tprsum / nrocs)
return fpravg, tpravg
# 計(jì)算對(duì)應(yīng)threshold的fpr和tpr
def roc_point_at_threshold(fpr, tpr, thresholds, thresh):
i = 0
while i < len(fpr) - 1 and thresholds[i] > thresh:
i += 1
return fpr[i], tpr[i]
五、最后
本文由淺入深地詳細(xì)介紹了 ROC 曲線算法,包含算法原理、公式、計(jì)算、源碼實(shí)現(xiàn)和講解,希望能夠幫助讀者一口氣(看的時(shí)候可得喘氣 ?????)搞懂 ROC。
雖然 ROC 是個(gè)不起眼的知識(shí)點(diǎn),但能網(wǎng)上能徹底講清楚 ROC 的文章并不多。所以我又花時(shí)間重溫了一遍 Tom Fawcett 的經(jīng)典論文《An introduction to ROC analysis》[4],并將論文的內(nèi)容抽絲剝繭、配上通俗易懂的 Python 代碼,最終寫出了這篇文章。再次致敬?? Tom Fawcett,感謝他在機(jī)器學(xué)習(xí)領(lǐng)域的貢獻(xiàn)!
作者:PrimiHub-Kevin
參考資料
《An introduction to ROC analysis》: https://www.researchgate.net/profile/Tom-Fawcett/publication/222511520_Introduction_to_ROC_analysis/links/5ac7844ca6fdcc8bfc7fa47e/Introduction-to-ROC-analysis.pdf
[2]《An Introduction to ROC Analysis》: https://www.researchgate.net/profile/Tom-Fawcett/publication/222511520_Introduction_to_ROC_analysis/links/5ac7844ca6fdcc8bfc7fa47e/Introduction-to-ROC-analysis.pdf
[3]roc_curve 函數(shù): https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html
[4]《An introduction to ROC analysis》: https://www.researchgate.net/profile/Tom-Fawcett/publication/222511520_Introduction_to_ROC_analysis/links/5ac7844ca6fdcc8bfc7fa47e/Introduction-to-ROC-analysis.pdf
長(zhǎng)按或掃描下方二維碼,后臺(tái)回復(fù):加群,即可申請(qǐng)入群。一定要備注:來源+研究方向+學(xué)校/公司,否則不拉入群中,見諒!
(長(zhǎng)按三秒,進(jìn)入后臺(tái))
推薦閱讀

