深度學(xué)習(xí)的“瓶頸”與“遛狗”定理

來(lái)源:老顧談幾何 本文約3900字,建議閱讀9分鐘
本文與你討論深度學(xué)習(xí)的模式坍塌問(wèn)題。
深度學(xué)習(xí)的社會(huì)學(xué)瓶頸
深度學(xué)習(xí)在工程技術(shù)領(lǐng)域取得了巨大的成功,其內(nèi)在原因在于自然數(shù)據(jù)集具有內(nèi)在的規(guī)律:流形分布定律,即一類(lèi)自然數(shù)據(jù)可以被視為嵌入在高維背景空間中的低維數(shù)據(jù)流形上的一個(gè)概率分布。深度學(xué)習(xí)算法可以被解耦為學(xué)習(xí)流形結(jié)構(gòu)和學(xué)習(xí)概率分布。在深度學(xué)習(xí)算法中,流形結(jié)構(gòu)被表示為編碼映射和解碼映射,即數(shù)據(jù)流形的局部參數(shù)化;概率分布可以被表示成吉布斯勢(shì)能函數(shù),或者最優(yōu)傳輸映射。最優(yōu)傳輸映射將白噪聲(高斯或者均勻分布)映射成數(shù)據(jù)分布。所有的映射,編碼、解碼、傳輸映射等都被深度神經(jīng)網(wǎng)絡(luò)來(lái)逼近。
由幾何逼近理論,我們從離散采樣點(diǎn)集合來(lái)重建數(shù)據(jù)流形,目的是保證重建流形與初始數(shù)據(jù)流形一致。這里,所謂一致具有不同層面的含義,通常由弱到強(qiáng)指拓?fù)浣Y(jié)構(gòu),Hausdorff距離,黎曼度量和微分算子的一致性,需要不同的采樣要求。例如曲率高的區(qū)域、內(nèi)射半徑小的區(qū)域、數(shù)據(jù)分布密度高的區(qū)域需要更加稠密的采樣。由此可見(jiàn),為了訓(xùn)練深度學(xué)習(xí)模型,我們需要數(shù)據(jù)流形上的稠密采樣點(diǎn),并且采樣點(diǎn)的分布忠實(shí)地反映了真實(shí)數(shù)據(jù)分布規(guī)律。因此,我們需要大量訓(xùn)練數(shù)據(jù)。
但是,很多大數(shù)據(jù)與個(gè)人隱私相關(guān),具有強(qiáng)烈的敏感性,無(wú)法直接公開(kāi)提供給社會(huì)各界使用,這成為未來(lái)深度學(xué)習(xí)的社會(huì)學(xué)方面的瓶頸。生成模型是突破瓶頸、實(shí)現(xiàn)數(shù)據(jù)脫敏的一種強(qiáng)有力的技術(shù)方法。例如,人臉圖像數(shù)據(jù)集會(huì)泄露人臉信息,侵犯?jìng)€(gè)人隱私;但是對(duì)于深度學(xué)習(xí)人臉識(shí)別算法,我們由需要大量人臉圖像用于訓(xùn)練和提高模型性能。這時(shí)我們可以應(yīng)用生成模型來(lái)生成大量的人臉圖片,這些圖片看上去與真人無(wú)異,但是現(xiàn)實(shí)生活中并不存在,因此不會(huì)侵犯任何人的隱私,同時(shí)也可以幫助人臉識(shí)別模型提高性能。

圖0. 生成的人臉圖像不具備社會(huì)學(xué)意義,同時(shí)反映了真實(shí)數(shù)據(jù)的統(tǒng)計(jì)特性
這種方法的理論詮釋如下:假如我們確切掌握了數(shù)據(jù)流形的信息和數(shù)據(jù)的分布,我們用數(shù)論方法產(chǎn)生偽隨機(jī)變量滿(mǎn)足均勻分布,用最優(yōu)傳輸映射和解碼映射變換成數(shù)據(jù)流形上的隨機(jī)變量,滿(mǎn)足數(shù)據(jù)分布,如此得到生成采樣,即為生成的人臉圖片。由幾何測(cè)度理論,數(shù)據(jù)流形為連續(xù)統(tǒng),訓(xùn)練數(shù)據(jù)集為離散點(diǎn)集,因此生成采樣落在訓(xùn)練數(shù)據(jù)集的概率為零。(在實(shí)際算法中,也可以加上限制以避免生成采樣落在訓(xùn)練集內(nèi))即便編碼、解碼映射與最優(yōu)傳輸映射完全公開(kāi),用戶(hù)由生成人臉圖片可以回溯到計(jì)算機(jī)生成的隨機(jī)數(shù),但是這個(gè)隨機(jī)數(shù)沒(méi)有任何社會(huì)學(xué)意義,均勻分布的信息熵最大,信息泄露最少。
同時(shí),這種方法保持了數(shù)據(jù)集的統(tǒng)計(jì)特性,生成數(shù)據(jù)集符合真正數(shù)據(jù)分布,因此對(duì)于基于統(tǒng)計(jì)特性的實(shí)際應(yīng)用而言,生成數(shù)據(jù)完美地解答了他們所關(guān)心的問(wèn)題。例如,一家服裝設(shè)計(jì)公司,他們需要各種人體形狀在人群中的分布情況,以決定各種尺碼服裝的生產(chǎn)比例。這種信息可以通過(guò)統(tǒng)計(jì)生成數(shù)據(jù)來(lái)計(jì)算出來(lái)。由此可見(jiàn),依隨人們?nèi)找嬷匾晹?shù)據(jù)安全和隱私保護(hù),生成模型的應(yīng)用會(huì)更加廣泛和深入。
深度學(xué)習(xí)的算法瓶頸
深度學(xué)習(xí)的一個(gè)主要算法瓶頸是所謂的模式坍塌(模式崩潰 mode collapse)問(wèn)題,具體表現(xiàn)為模型對(duì)于超參數(shù)過(guò)于敏感,訓(xùn)練收斂困難,誤差長(zhǎng)期震蕩;如果數(shù)據(jù)分布具有多個(gè)模式,生成數(shù)據(jù)會(huì)丟失一些模式,或者生成數(shù)據(jù)會(huì)覆蓋所有模式,但是同時(shí)生成模式之外的失真數(shù)據(jù)。
模式坍塌的內(nèi)在原因可以分析如下:深度學(xué)習(xí)中所有的映射都用深度神經(jīng)網(wǎng)絡(luò)來(lái)逼近,但是深度網(wǎng)絡(luò)只能表達(dá)連續(xù)映射;但是概率分布之間的傳輸變換有可能是非連續(xù)變換。這一本質(zhì)矛盾導(dǎo)致了模式坍塌。那么是在什么情形下,最優(yōu)傳輸映射是非連續(xù)的呢?這需要由最優(yōu)傳輸映射正則性理論來(lái)回答。雖然最優(yōu)傳輸理論已經(jīng)發(fā)展了兩百多年,傳統(tǒng)的數(shù)學(xué)家們只關(guān)心連續(xù)的最優(yōu)傳輸映射,對(duì)于非連續(xù)的奇異集合沒(méi)有太多研究,因此最優(yōu)傳輸映射奇異集合理論一直處于尚未深入探索的階段。深度學(xué)習(xí)的興起,將會(huì)燃起數(shù)學(xué)家們巨大的熱情,這一領(lǐng)域的發(fā)展將會(huì)迎來(lái)一次飛躍。
最優(yōu)傳輸理論
我們回憶一下經(jīng)典的最優(yōu)傳輸理論。給定分布定義在開(kāi)集上,和分布在上,滿(mǎn)足平衡條件。映射被稱(chēng)為是保測(cè)度的,如果對(duì)一切Borel集合,都有。給定傳輸代價(jià)函數(shù), 蒙日問(wèn)題在所有保測(cè)度映射中尋找傳輸總代價(jià)最小者,
蒙日問(wèn)題的解被稱(chēng)為是最優(yōu)傳輸映射。
Brenier理論表明,在較為一般的情形下,存在定義在上的凸函數(shù),被稱(chēng)為是 Brenier勢(shì)能函數(shù),其梯度映射給出了最優(yōu)傳輸映射,。由保測(cè)度條件,我們可以得到Monge-Ampere方程, 假設(shè)密度函數(shù)為并且, 我們有
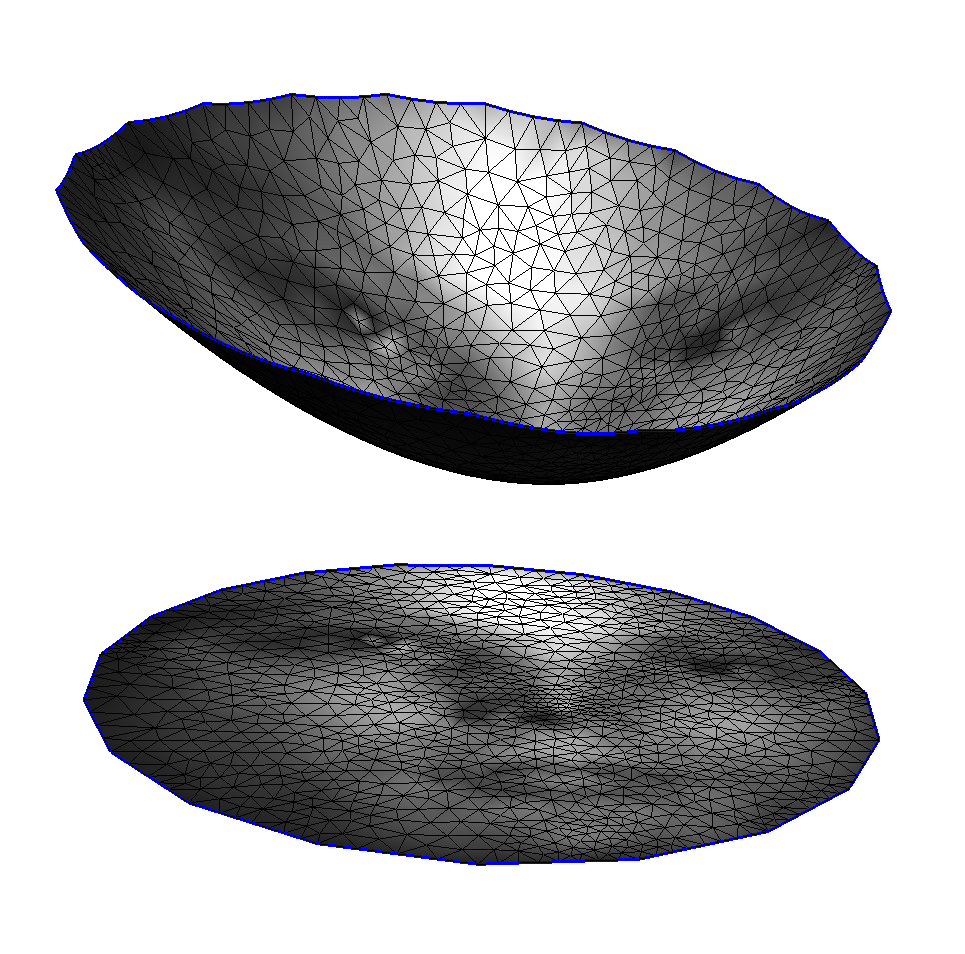 | 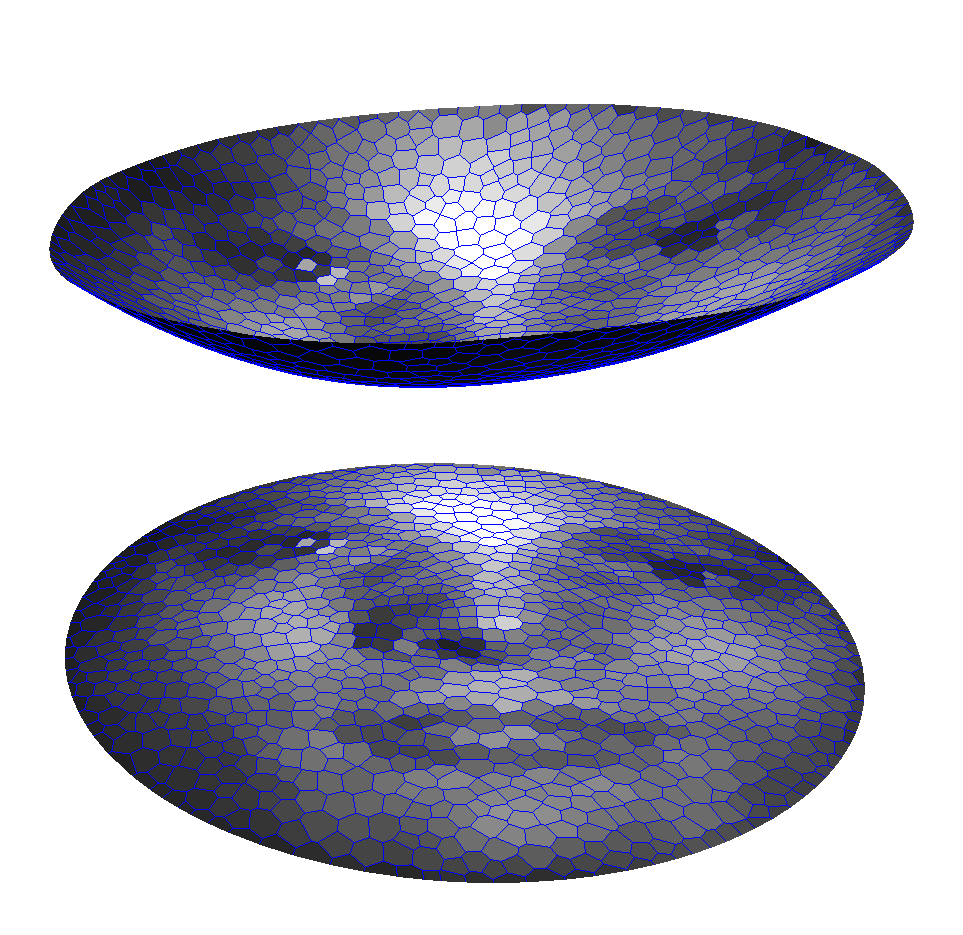 |
圖1. 如果源區(qū)域和目標(biāo)區(qū)域都是凸集,密度函數(shù)光滑,則Brenier勢(shì)能光滑
經(jīng)典的Monge-Ampere方程正則性理論都假設(shè)和是凸集合,例如密度函數(shù)滿(mǎn)足光滑性條件,,這時(shí)Brenier勢(shì)能函數(shù),最優(yōu)傳輸映射光滑,不存在奇異集合。如圖1所示,和都是單位圓盤(pán),Brenier勢(shì)能函數(shù)光滑,最優(yōu)傳輸映射連續(xù),不存在奇異集合。
 |
|
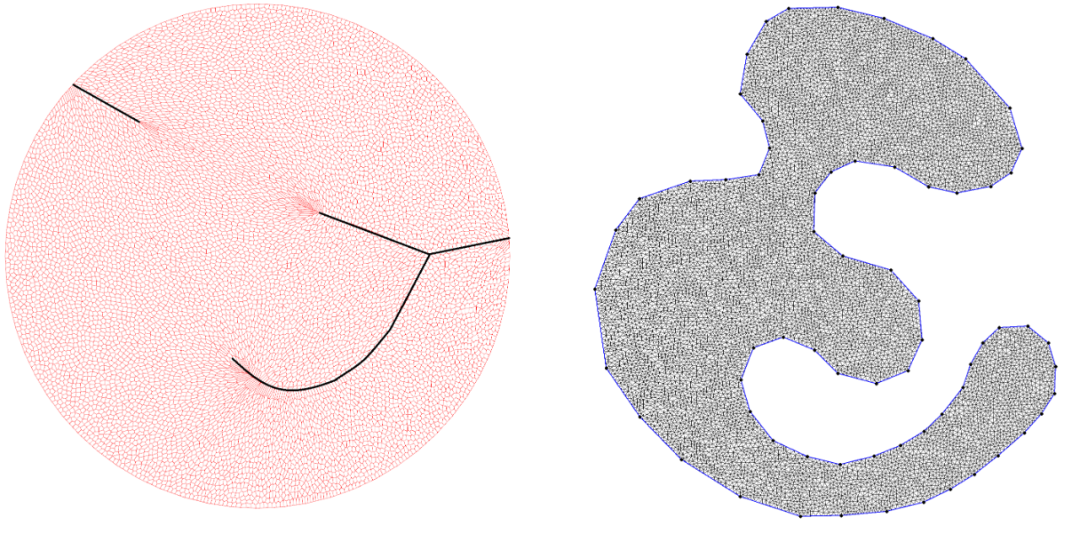
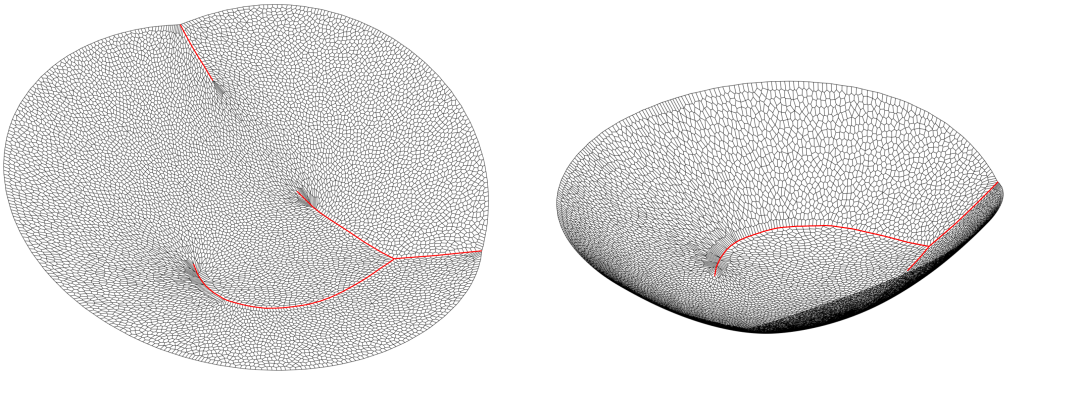
圖2. 如果目標(biāo)區(qū)域非凸,則最優(yōu)傳輸映射非連續(xù),Brenier勢(shì)能非光滑
如圖2所示,我們計(jì)算從單位圓盤(pán)上的均勻分布到海馬區(qū)域上的分布區(qū)域之間的最優(yōu)傳輸映射(下行),則Brenier勢(shì)能函數(shù)(上行)全局連續(xù),但是沿著紅色曲線不可微分。在單位圓盤(pán)上,紅色曲線的投影是黑色的曲線,被稱(chēng)為是奇異集合,最優(yōu)傳輸映射在奇異集合上間斷。因此,傳輸映射是非連續(xù)映射。如果目標(biāo)區(qū)域接近凸集,那么有可能最優(yōu)傳輸映射依然是連續(xù)的。
一個(gè)自然的問(wèn)題在于:奇異集合存在的充分必要條件是什么?這個(gè)問(wèn)題的解答與深度學(xué)習(xí)中的模式坍塌具有本質(zhì)聯(lián)系。這里我們用區(qū)域邊界的曲率給出一個(gè)充分條件,即所謂的“遛狗”定理。
“遛狗”定理
如圖3左幀所示,假設(shè)有一位朋友遛狗,這位朋友在平面上的軌跡是一條封閉曲線,狗的軌跡是另外一條封閉曲線,人和狗都是逆時(shí)針行走,在任意時(shí)刻,在各自軌道上一直面向前方,從不回頭(但是走過(guò)一圈,整體上繞回到起點(diǎn))。
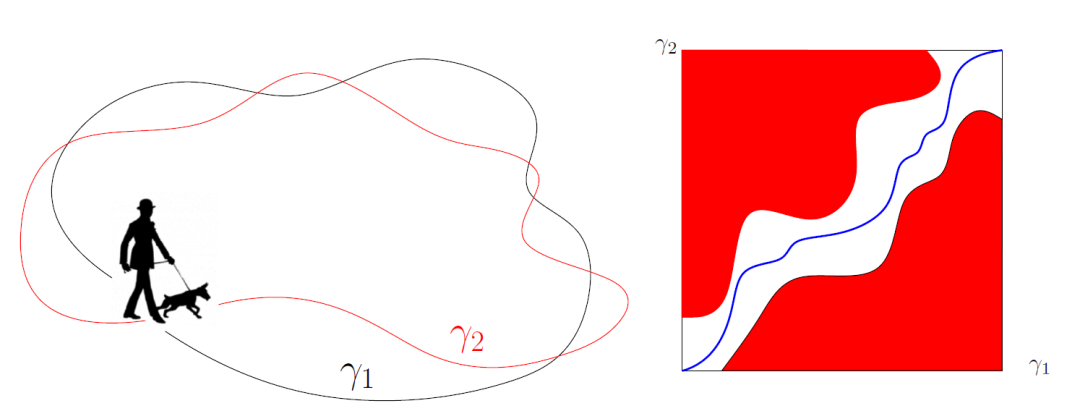
圖3. 在各種遛狗方式中,最短的牽狗繩長(zhǎng)度等于曲線間的Frechet距離
Frechet 距離:
同一時(shí)刻人和狗的位置之間有個(gè)對(duì)應(yīng)關(guān)系,這自然給出了軌道間的一個(gè)同胚映射,等價(jià)的我們用參數(shù)來(lái)表示。由人和狗都不回頭的假定,我們自然有對(duì)于任意時(shí)刻都成立。那么不同的遛狗方式對(duì)應(yīng)著不同的同胚映射。如果固定一個(gè)遛狗方式,牽狗繩的長(zhǎng)度不小于人和狗之間任意時(shí)刻的最大距離。在所有可能的遛狗方式中,最短的牽狗繩長(zhǎng)度等于:

我們將可能的最短牽狗繩長(zhǎng)度定義為和的Frechet距離。
在計(jì)算幾何中,人們對(duì)于Frechet距離的算法已經(jīng)有了充分的研究。如圖3右?guī)荆覀冇脵M軸表示的參數(shù),縱軸表示的參數(shù)。任何同胚映射,滿(mǎn)足可以表示成一條連接對(duì)角點(diǎn)的曲線,曲線在水平和鉛直兩個(gè)方向都是單調(diào)的。給定一個(gè),對(duì)于正方形內(nèi)任意一點(diǎn),如果,我們將其繪為紅色,反之為白色。那么白色區(qū)域?yàn)樽杂蓞^(qū)域,紅色區(qū)域?yàn)榻箙^(qū)域。如果白色區(qū)域中存在一條水平、鉛直都單調(diào)的曲線,連接對(duì)角點(diǎn),則這兩條曲線的Frechet距離小于。實(shí)際計(jì)算中,我們可以用二分法來(lái)搜索,找到的Frechet距離。
法向Frechet距離:
類(lèi)似的,假如和的正則性較好,例如它們是光滑的,則沿著曲線法向量是良定義的。由此我們可以定義法向Frechet距離:我們將人和狗所在位置之間的距離換成人和狗所在點(diǎn)處的外法向量之間的距離,寫(xiě)成公式就是:
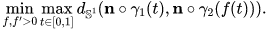
這里是單位圓上的測(cè)地距離。
傾斜條件:
給定平面區(qū)域間的最優(yōu)傳輸映射,邊界曲線和是二階光滑的,滿(mǎn)足一定的光滑性條件,那么最優(yōu)傳輸映射可以拓展到邊界上,,并且滿(mǎn)足所謂的傾斜性條件(Obliqueness Condition),即給定邊界上一點(diǎn),
即邊界點(diǎn)的法向量和對(duì)應(yīng)像點(diǎn)的法向量夾角小于等于直角。
遛狗定理:
假設(shè)已知定義在平面區(qū)域上概率分布,和,這里概率密度函數(shù)滿(mǎn)足比較寬泛的正則性條件,邊界曲線和是二階光滑;如果和的法向Frechet距離大于,則最優(yōu)傳輸映射非連續(xù),存在奇異集合。假如最優(yōu)傳輸映射不存在奇異集合,Brenier勢(shì)能函數(shù)全局可微,那么可以拓展到邊界上,并且在邊界上的限制是同胚,并且滿(mǎn)足傾斜條件,因此和的法向Frechet距離不大于直角,矛盾。于是我們得出結(jié)論:存在奇異集合,最優(yōu)傳輸映射在奇異集合上間斷。
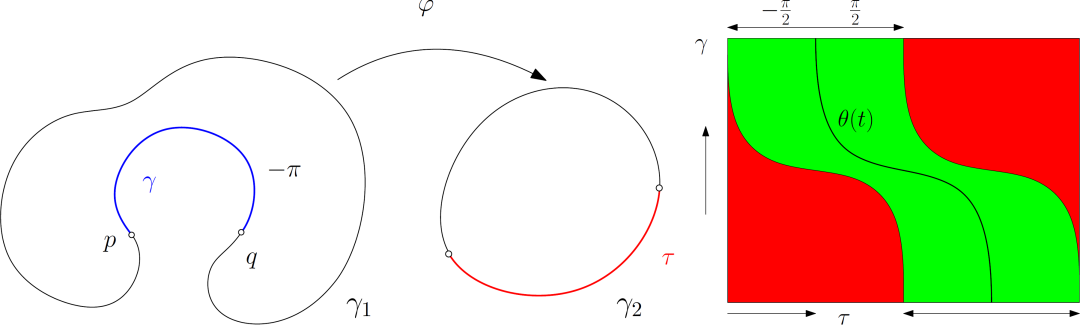
圖4. 奇異集合存在的曲率條件
曲率條件:
由遛狗定理,我們可以給出一些最優(yōu)傳輸映射存在奇異點(diǎn)的曲率條件。如圖4左幀所示,如果有一段曲線,總曲率小于,即存在,
為凸集,那么最優(yōu)傳輸映射必定存在奇異集合。如圖4右?guī)荆瑱M軸為,縱軸為。兩條曲線都采用弧長(zhǎng)參數(shù)。對(duì)于任意一點(diǎn),如果處的法向量與處的法向量夾角大于,我們將其繪為紅色,否則為綠色。則綠色區(qū)域?yàn)樽杂蓞^(qū)域。的起點(diǎn)為,的終點(diǎn)為,右側(cè)長(zhǎng)方形底邊對(duì)應(yīng),頂邊對(duì)應(yīng)。底邊和頂邊的綠色區(qū)域恰好互補(bǔ),那么綠色區(qū)域中不存在沿著水平方向和鉛直方向都單調(diào)的曲線。這意味著和的法向Frechet距離一定大于,必然存在奇異集合,最優(yōu)傳輸映射在奇異集合上非連續(xù)。這種情形下,最優(yōu)傳輸映射無(wú)法用深度神經(jīng)網(wǎng)絡(luò)直接表示。
推廣和展望
高維的最優(yōu)傳輸映射比平面上的最優(yōu)傳輸映射復(fù)雜,但是同樣的想法可以推廣。例如在三維情形,假設(shè)是三維空間中的區(qū)域,其邊界和是光滑曲面,其法向Frechet距離定義為:

如果法向Frechet距離大于,則最優(yōu)傳輸映射存在奇異集合。遛狗定理給出了奇異集合存在的充分條件,必要條件目前尚未清楚。奇異集合的拓?fù)淇坍?huà)依然存在很多開(kāi)放的問(wèn)題。這些基本問(wèn)題需要基礎(chǔ)數(shù)學(xué)家給出解答。
在深度學(xué)習(xí)中,隱空間中的數(shù)據(jù)分布支集往往具有復(fù)雜拓?fù)洌瑤缀紊弦膊痪邆渫剐裕瑐鬏斢成洳豢杀苊獾卮嬖谄娈惣希虼松疃壬窠?jīng)網(wǎng)絡(luò)無(wú)法表達(dá)這種非連續(xù)的映射。為了避免模式坍塌,我們可以用神經(jīng)網(wǎng)絡(luò)表達(dá)Brenier勢(shì)能函數(shù),或者采用特定的數(shù)值逼近方法。另一方面,Monge-Ampere方程強(qiáng)烈非線性,高維最優(yōu)傳輸映射計(jì)算復(fù)雜度很高。如何設(shè)計(jì)更加高效的算法,和更加適合求解的硬件,這也為計(jì)算機(jī)科學(xué)家提出了挑戰(zhàn)。
我們相信未來(lái)最優(yōu)傳輸映射的正則性理論會(huì)進(jìn)一步發(fā)展,能夠給出奇異集合的深刻洞察和刻畫(huà),從而更好地指導(dǎo)深度學(xué)習(xí)的統(tǒng)計(jì)理論;也相信深度學(xué)習(xí)領(lǐng)域會(huì)有更多基于最優(yōu)傳輸理論的模型被提出并深入探索,從根本上克服模式坍塌等瓶頸問(wèn)題,并且使得黑箱變得透明。
編輯:黃繼彥
校對(duì):汪雨晴