基于邊緣檢測(cè)的圖像分割算法!
圖像處理
Author:louwill
Machine Learning Lab
從本文開始,筆者計(jì)劃花一些時(shí)間對(duì)傳統(tǒng)的圖像分割算法進(jìn)行一個(gè)系統(tǒng)的梳理,敘述方式仍然是以原理闡述和代碼實(shí)現(xiàn)為主。
談到圖像分割算法,現(xiàn)在基本上言必稱深度學(xué)習(xí)。這也無可厚非,畢竟大環(huán)境和研究趨勢(shì)如此。但回過頭來,我們有必要對(duì)傳統(tǒng)的圖像處理算法有一個(gè)基本的了解。本文的主要內(nèi)容是對(duì)基于邊緣檢測(cè)的圖像分割算法進(jìn)行介紹。主要敘述內(nèi)容包括圖像濾波、邊緣檢測(cè)原理與思想、基礎(chǔ)邊緣檢測(cè)梯度算子和高級(jí)邊緣檢測(cè)梯度算子。
圖像濾波與邊緣檢測(cè)
在數(shù)字圖像處理領(lǐng)域,圖像濾波是一個(gè)重要是知識(shí)點(diǎn)。關(guān)于濾波的相關(guān)知識(shí),不是本文的重點(diǎn)所在,這里我們重點(diǎn)說一下圖像濾波與邊緣檢測(cè)之間的關(guān)系。
圖像濾波一般有兩個(gè)目的,一個(gè)是用于圖像特征的提取,這一點(diǎn)跟深度學(xué)習(xí)中的卷積核原理是一樣的。另外一個(gè)則是通過濾波做一些去噪相關(guān)的預(yù)處理工作。與深度學(xué)習(xí)中的卷積核一樣,邊緣檢測(cè)也是基于圖像特征的思路,用于圖像關(guān)鍵特征的提取。

圖1 圖像濾波與圖像扭曲
邊緣檢測(cè)是一種基于圖像灰度突變和不連續(xù)性來分割圖像的方法。而檢測(cè)這種灰度突變和不連續(xù)性正是依靠濾波器來實(shí)現(xiàn)。下面,我們先引入圖像梯度的概念,然后再介紹基本的圖像梯度算子。
為了達(dá)到尋找圖像邊緣的目的,檢測(cè)灰度變化可以用梯度來實(shí)現(xiàn)。圖像梯度定義如下,給定一幅圖像,其在位置的圖像梯度可定義為:
該向量有一個(gè)重要的幾何性質(zhì),即指出了在位置處的最大變化率的方向。
由上式可知,要得到一幅圖像的梯度,需要在圖像每個(gè)像素處計(jì)算偏導(dǎo)數(shù)和:
上述兩個(gè)公式對(duì)所有的和的有關(guān)值可以用圖2的一維模板通過對(duì)的濾波來執(zhí)行。
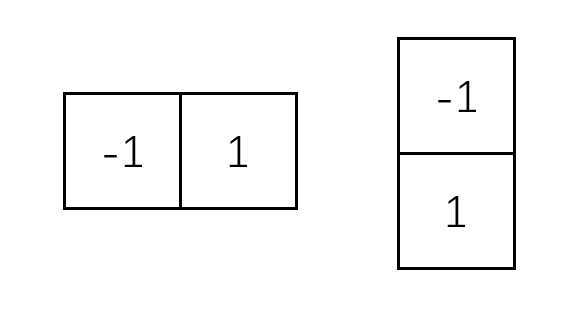
圖2 圖像梯度一維模板
基礎(chǔ)邊緣檢測(cè)梯度算子
類似于圖2這種用于計(jì)算圖像梯度的濾波器模板,也稱為梯度算子或者邊緣算子。基于不同的濾波器模板,我們可以提取圖像不同的特征,從而得到不同的邊緣檢測(cè)效果。
基礎(chǔ)的邊緣檢測(cè)梯度算子包括Roberts算子、Prewitts算子以及Sobel算子等。
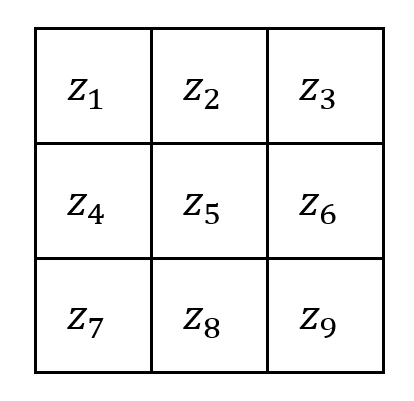
圖3 一幅圖像的3*3區(qū)域
Roberts算子也叫交叉梯度算子,用于提取圖像對(duì)角線的邊緣特征。當(dāng)我們對(duì)圖像對(duì)角線邊緣信息感興趣時(shí),可以使用該算子。如圖3所示的區(qū)域,Roberts算子以求對(duì)角像素之差為基礎(chǔ)。
可以看到,Roberts算子實(shí)際上用的是模板。如果對(duì)于大小的模板來給出偏導(dǎo)數(shù)的數(shù)值近似,有:
在上式子中,區(qū)域的第三行與第一行之差近似為方向的梯度,第三列和第一列之差近似為方向的導(dǎo)數(shù),這種梯度算子即Prewitts算子。
如果我們對(duì)上式做一些輕微的變化,將中間值的系數(shù)改為,如下式所示:
對(duì)中間位置加一個(gè)的系數(shù)能夠起到平滑圖像的作用,這種算子即Sobel算子。
Roberts算子、Prewitts算子和Sobel算子用到的梯度模板如圖4所示。
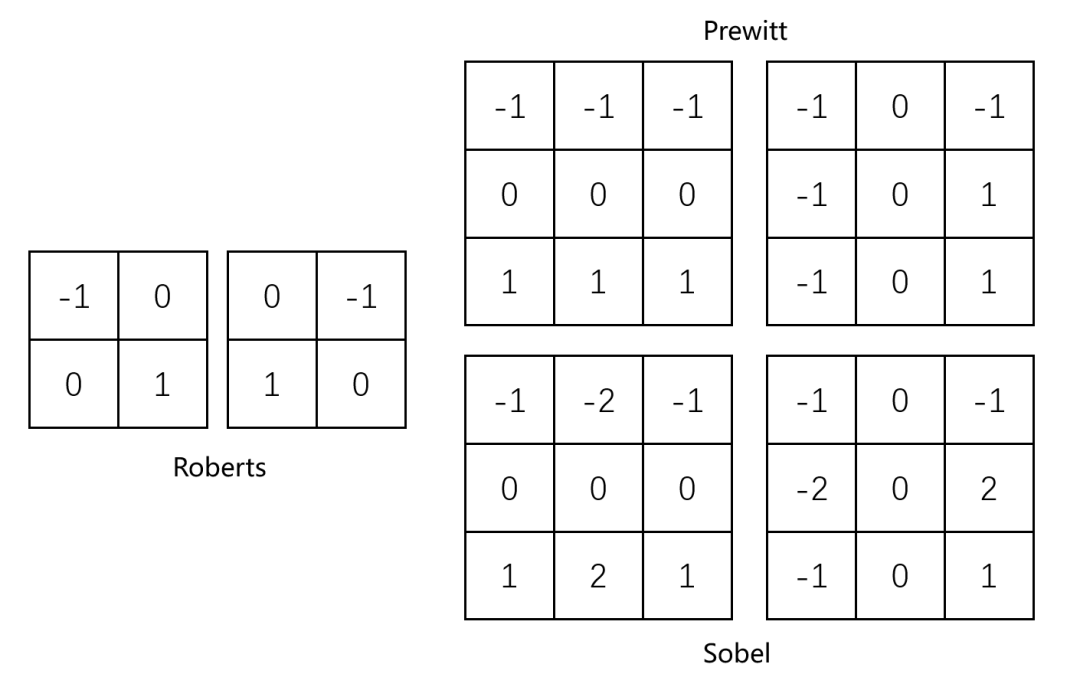
圖4 基礎(chǔ)邊緣檢測(cè)算子模板
高級(jí)邊緣檢測(cè)梯度算子
Roberts算子、Prewitts算子和Sobel算子這些基礎(chǔ)梯度算子都有一定的邊緣檢測(cè)效果,但都是完全基于濾波器的檢測(cè)方法,沒有對(duì)圖像特性和圖像噪聲采取預(yù)防措施,所以會(huì)限制其檢測(cè)能力。一些高級(jí)的邊緣檢測(cè)梯度算子會(huì)在考慮圖像特性和圖像噪聲的基礎(chǔ)上,對(duì)初級(jí)的邊緣檢測(cè)算法進(jìn)行改進(jìn)。典型的高級(jí)邊緣檢測(cè)梯度算子包括Canny算子和Marr-Hildreth算子。
Canny算子
Canny算子是一種多級(jí)邊緣檢測(cè)算法,本身也是一種基于濾波器的檢測(cè)算法,但是在濾波的基礎(chǔ)上加了非極大值抑制和雙閾值處理。
Canny認(rèn)為,一個(gè)好的邊緣檢測(cè)算法,應(yīng)該有如下三個(gè)特征:
低錯(cuò)誤率。即所有邊緣都能被找到,并且偽邊緣點(diǎn)最少。 好的定位。定位的邊緣要與真實(shí)邊緣盡可能的接近。 單一響應(yīng)。對(duì)于真實(shí)的邊緣點(diǎn),檢測(cè)算法僅能返回一個(gè)點(diǎn)。
Canny算子的設(shè)計(jì)邏輯主要是將上述三個(gè)原則進(jìn)行數(shù)學(xué)化的規(guī)約和設(shè)計(jì)。Canny算子的基本步驟如下:
對(duì)輸入圖像使用高斯濾波器進(jìn)行平滑處理 對(duì)平滑后的圖像計(jì)算梯度幅值圖像和角度圖像 對(duì)梯度幅值圖像應(yīng)用非極大值抑制 對(duì)非極大值抑制之后的圖像進(jìn)行雙閾值處理
下面我們來看一下Canny算子每個(gè)步驟的具體操作過程。令為輸入圖像,為二維高斯函數(shù),有:
用對(duì)進(jìn)行高斯濾波處理即可。假設(shè)經(jīng)過高斯濾波平滑后的圖像為,有:
然后基于計(jì)算梯度幅值圖像和角度圖像,計(jì)算公式如下:
其中,,。
上一步得到的梯度幅值圖像可能會(huì)存在邊緣粗寬、弱邊緣干擾等問題。所以接下來就是對(duì)梯度幅值圖像進(jìn)行非極大值抑制,找到圖像的局部最大值,將局部非極大值設(shè)為0。最后再補(bǔ)充一個(gè)雙閾值處理,用來減少偽邊緣點(diǎn)。主要思路是設(shè)定兩個(gè)閾值,一個(gè)低閾值,一個(gè)高閾值,將小于低閾值的點(diǎn)作為假邊緣設(shè)為0,將大于高閾值的點(diǎn)作為強(qiáng)邊緣設(shè)為1。
基于opencv的Canny邊緣檢測(cè)示例如下代碼所示。
import numpy as np
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('kobe.jpg', 0)
edges = cv2.Canny(img, 40, 80)
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(edges, cmap='gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])
plt.show();

圖5 Canny算子檢測(cè)效果
Marr-Hildreth算子
Marr和Hildreth通過研究證明了:
圖像的灰度變化與尺寸無關(guān),所以需要使用不同尺寸的算子。 灰度的突然變化會(huì)在一階導(dǎo)數(shù)上體現(xiàn)為波峰或波谷,在二階導(dǎo)數(shù)上產(chǎn)生零交叉。
兩人又通過研究論證,滿足上述兩個(gè)條件的最好的檢測(cè)算子為,其中為拉普拉斯算子,為標(biāo)準(zhǔn)差為的二維高斯函數(shù):
由上式可得的表達(dá)式為:
整理各項(xiàng)后可得到如下表達(dá)式:
上式稱為高斯拉普拉斯(LoG),因?yàn)槠湫螤钕褚粋€(gè)草帽,所以也叫墨西哥草帽算子,如圖6所示。
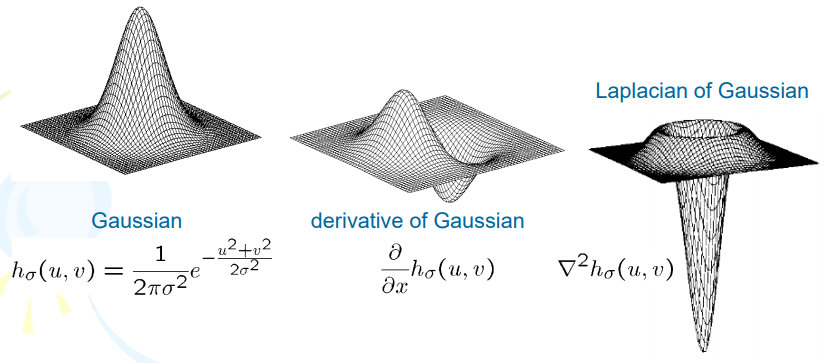
圖6 高斯拉普拉斯
所以,Marr-Hildreth算子是對(duì)輸入圖像做LoG濾波處理,然后在輸出圖像中尋找零交叉來確定邊緣位置。
小結(jié)
本文在介紹圖像濾波器的基礎(chǔ)上,介紹了圖像梯度的概念。繼而介紹了基本的邊緣檢測(cè)算子,包括Roberts算子、Prewitts算子以及Sobel算子等。但基礎(chǔ)的邊緣檢測(cè)算子都有其局限性,在實(shí)際應(yīng)用中,Canny算子和Marr-Hildreth算子等典型的高級(jí)邊緣檢測(cè)梯度算子具備更好的應(yīng)用效果和泛化性能。
參考資料
[1] 數(shù)字圖像處理
[2] https://learnopencv.com/edge-detection-using-opencv/
往期精彩:
