Go 刷 leetcode｜割冷凍韭菜的最佳時機

今天為大家講解 LeetCode 第 309 題，是昨天帶來的 《Go?leetcode｜割韭菜的最佳時機》?的一個升級版，不了解的朋友建議先去看看。

題目描述

給定一個整數(shù)數(shù)組，其中第 i 個元素代表了第 i 天的股票價格 。

設計一個算法計算出最大利潤。在滿足以下約束條件下，你可以盡可能地完成更多的交易（多次買賣一支股票）:

你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。賣出股票后，你無法在第二天買入股票 (即冷凍期為 1 天)。示例:

輸入: [1,2,3,0,2] 輸出: 3 解釋: 對應的交易狀態(tài)為: [買入, 賣出, 冷凍期, 買入, 賣出]

來源：力扣（LeetCode） 鏈接：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown 著作權歸領扣網(wǎng)絡所有。商業(yè)轉(zhuǎn)載請聯(lián)系官方授權，非商業(yè)轉(zhuǎn)載請注明出處。

解題思路

動態(tài)規(guī)劃

了解的朋友可能知道「買股票」有一系列的題目，可以的話我會一一講解。

這一系列的題也正涉及了重要的「動態(tài)規(guī)劃」

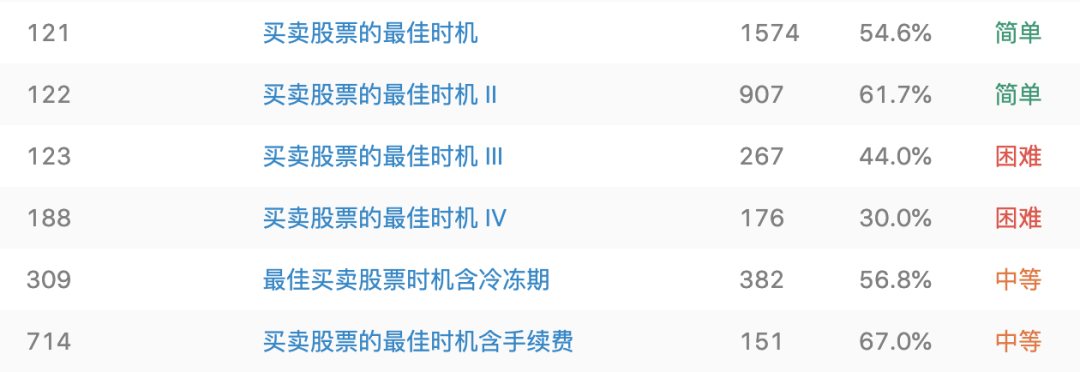
這里先區(qū)別一下「買股票」系列中這道題的不同：

這道題增加了「冷凍期」這樣一個條件，沒有限制多少筆交易。因此只需要增加一個狀態(tài)。

第一步：狀態(tài)定義

dp[i][j] 表示[0, i]區(qū)間內(nèi)，在下標為i這一天狀態(tài)為j時的最大收益。

這里j取三個值：

• 0 表示不持股；
• 1 表示持股；
• 2 表示處在冷凍期。

第二部：狀態(tài)轉(zhuǎn)移方程

這步是至關重要也是最難的，得知狀態(tài)轉(zhuǎn)移方程的關鍵是理解題意，理清邏輯。

• 不持股可以由這兩個狀態(tài)轉(zhuǎn)換而來：昨天不持股，今天什么都不操作，仍然不持股；昨天持股，今天賣了一股。
• 持股可以由這兩個狀態(tài)轉(zhuǎn)換而來：昨天持股，今天什么都不操作，仍然持股；昨天處在冷凍期，今天買了一股；
• 處在冷凍期比較特殊，只可以由不持股轉(zhuǎn)換而來，因為題目中說，剛剛把股票賣了，需要冷凍 1 天。（持股賣了變成不持股，再變成冷凍期）

以上分析可以用下圖表示：

第三步：初始化（base case）

在第 0 天，不持股的初始化值為 0，

持股的初始化值為 -prices[0]（表示購買了一股），

雖然不處于冷凍期，但是初始化的值可以為 0。

第四步：返回值

每一天都由前面幾天的狀態(tài)轉(zhuǎn)換而來，最優(yōu)值在最后一天。取不持股和冷凍期的最大者。

代碼實現(xiàn)

//go
func?maxProfit(prices?[]int)?int?{
?length?:=?len(prices)
?//?特殊判斷
?if?length?<=?1?{
??return?0
?}
?//?聲明dp
?dp?:=?make([][3]int,?length)
?//?初始化
?dp[0][0]?=?0??????????//?【0天】【不持股】
?dp[0][1]?=?-prices[0]?//?【0天】【持股】
?dp[0][2]?=?0??????????//?【0天】【冷凍期】

?for?i?:=?1;?i???//?【第i天】【不持股】?=?max（昨天不持股今天不操作，昨天持股+今天賣一股）
??dp[i][0]?=?max(dp[i-1][0],?dp[i-1][1]+prices[i])
??//?【第i天】【持股】?=?max（昨天持股今天不操作，昨天冷凍期+今天買一股）
??dp[i][1]?=?max(dp[i-1][1],?dp[i-1][2]-prices[i])
??//?【第i天】【冷凍期】?=?昨天賣了不持股
??dp[i][2]?=?dp[i-1][0]
?}

?//?返回不持股和冷凍期的最大者
?return?max(dp[length-1][0],?dp[length-1][0])
}

func?max(x,?y?int)?int?{
?if?x?>?y?{
??return?x
?}
?return?y
}

//java
public?class?Solution?{

????public?int?maxProfit(int[]?prices)?{
????????int?len?=?prices.length;
????????//?特判
????????if?(len?2)?{
????????????return?0;
????????}

????????int[][]?dp?=?new?int[len][3];

????????//?初始化
????????dp[0][0]?=?0;
????????dp[0][1]?=?-prices[0];
????????dp[0][2]?=?0;

????????for?(int?i?=?1;?i?????????????dp[i][0]?=?Math.max(dp[i?-?1][0],?dp[i?-?1][1]?+?prices[i]);
????????????dp[i][1]?=?Math.max(dp[i?-?1][1],?dp[i?-?1][2]?-?prices[i]);
????????????dp[i][2]?=?dp[i?-?1][0];
????????}
????????return?Math.max(dp[len?-?1][0],?dp[len?-?1][2]);
????}
}

鄭重聲明：

所展示代碼已通過 LeetCode 運行通過，請放心食用~