一篇簡(jiǎn)明的 JavaScript 函數(shù)式編程入門指南

什么是函數(shù)式編程
早在 1950 年代,隨著 Lisp 語(yǔ)言的創(chuàng)建,函數(shù)式編程( Functional Programming,簡(jiǎn)稱 FP)就已經(jīng)開始出現(xiàn)在大家視野。
而直到近些年,函數(shù)式以其優(yōu)雅,簡(jiǎn)單的特點(diǎn)開始重新風(fēng)靡整個(gè)編程界,主流語(yǔ)言在設(shè)計(jì)的時(shí)候無(wú)一例外都會(huì)更多的參考函數(shù)式特性( Lambda 表達(dá)式,原生支持 map ,reduce ……),Java8 開始支持函數(shù)式編程。
而在前端領(lǐng)域,我們同樣能看到很多函數(shù)式編程的影子:ES6 中加入了箭頭函數(shù),Redux 引入 Elm 思路降低 Flux 的復(fù)雜性,React16.6 開始推出 React.memo(),使得 pure functional components 成為可能,16.8 開始主推 Hook,建議使用 pure function 進(jìn)行組件編寫……
這些無(wú)一例外的說(shuō)明,函數(shù)式編程這種古老的編程范式并沒(méi)有隨著歲月而褪去其光彩,反而愈加生機(jī)勃勃。
另外還有一些例子能證明函數(shù)式編程也適應(yīng)于大型軟件的編寫:
WhatsApp:通過(guò) Erlang,WhatsApp 可以支持 9 億用戶,而其團(tuán)隊(duì)中只有 50 名工程師。
Discord:使用 Elixir,類似方式的 Discord 每分鐘處理超過(guò)一百萬(wàn)個(gè)請(qǐng)求。
于我個(gè)人而言,函數(shù)式編程就像第三次工業(yè)革命,前兩次分別為命令式編程(Imperative programming)和面向?qū)ο缶幊蹋∣bject Oriented Programming)。
初窺
概念說(shuō)的再多也不夠例子直觀
Talk is cheap, show me the code
假設(shè)我們有這么個(gè)需求,我們登記了一系列人名存在數(shù)組中,現(xiàn)在需要對(duì)這個(gè)結(jié)構(gòu)進(jìn)行一些修改,需要把字符串?dāng)?shù)組變成一個(gè)對(duì)象數(shù)組,方便后續(xù)的擴(kuò)展,并且需要把人名做一些轉(zhuǎn)換:
['john-reese', 'harold-finch', 'sameen-shaw']
// 轉(zhuǎn)換成
[{name: 'John Reese'}, {name: 'Harold Finch'}, {name: 'Sameen Shaw'}]
復(fù)制代碼
命令式編程
用傳統(tǒng)的編程思路,我們一上來(lái)就可以擼代碼,臨時(shí)變量,循環(huán)走起來(lái):
const arr = ['john-reese', 'harold-finch', 'sameen-shaw'];
const newArr = [];
for (let i = 0, len = arr.length; i < len ; i++) {
let name = arr[i];
let names = name.split('-');
let newName = [];
for (let j = 0, naemLen = names.length; j < naemLen; j++) {
let nameItem = names[j][0].toUpperCase() + names[j].slice(1);
newName.push(nameItem);
}
newArr.push({ name : newName.join(' ') });
}
return newArr;
復(fù)制代碼
完成,這幾乎是所有人下意識(shí)的編程思路,完全的面向過(guò)程。你會(huì)想我需要依次完成:
定義一個(gè)臨時(shí)變量 newArr。 我需要做一個(gè)循環(huán)。 循環(huán)需要做 arr.length 次。 每次把名字的首位取出來(lái)大寫,然后拼接剩下的部分。 …… 最后返回結(jié)果。
這樣當(dāng)然能完成任務(wù),最后的結(jié)果就是一堆中間臨時(shí)變量,光想變量名就讓人感到崩潰。同時(shí)過(guò)程中摻雜了大量邏輯,通常一個(gè)函數(shù)需要從頭讀到尾才知道它具體做了什么,而且一旦出問(wèn)題很難定位。
函數(shù)式
一直以來(lái),我也沒(méi)覺(jué)得這樣編程有什么問(wèn)題,直到我遇到了函數(shù)式編程。我們來(lái)看一看一個(gè) FPer 會(huì)如何思考這個(gè)問(wèn)題:
我只需要一個(gè)函數(shù)能實(shí)現(xiàn)從 String 數(shù)組到Object 數(shù)組的轉(zhuǎn)換:

convertNames :: [String] -> [Object]
復(fù)制代碼
這里面涉及到一個(gè) String -> Object的轉(zhuǎn)換,那我需要有這么個(gè)函數(shù)實(shí)現(xiàn)這種轉(zhuǎn)換:

convert2Obj :: String -> Object
復(fù)制代碼
至于這種轉(zhuǎn)換,可以輕松想到需要兩個(gè)函數(shù)完成:

capitalizeName:把名稱轉(zhuǎn)換成指定形式genObj:把任意類型轉(zhuǎn)換成對(duì)象如果再細(xì)想一下,
capitalizeName其實(shí)也是幾個(gè)方法的組合(split,join,capitalize),剩下的幾個(gè)函數(shù)都是非常容易實(shí)現(xiàn)的。
好了,我們的任務(wù)完成了,可以 運(yùn)行代碼
const capitalize = x => x[0].toUpperCase() + x.slice(1).toLowerCase();
const genObj = curry((key, x) => {
let obj = {};
obj[key] = x;
return obj;
})
const capitalizeName = compose(join(' '), map(capitalize), split('-'));
const convert2Obj = compose(genObj('name'), capitalizeName)
const convertName = map(convert2Obj);
convertName(['john-reese', 'harold-finch', 'sameen-shaw'])
復(fù)制代碼
你可以先忽略其中的 curry 和 compose 函數(shù)(后面 會(huì)介紹)。只是看這個(gè)編程思路,可以清晰看出,函數(shù)式編程的思維過(guò)程是完全不同的,它的著眼點(diǎn)是函數(shù),而不是過(guò)程,它強(qiáng)調(diào)的是如何通過(guò)函數(shù)的組合變換去解決問(wèn)題,而不是我通過(guò)寫什么樣的語(yǔ)句去解決問(wèn)題,當(dāng)你的代碼越來(lái)越多的時(shí)候,這種函數(shù)的拆分和組合就會(huì)產(chǎn)生出強(qiáng)大的力量。
為什么叫函數(shù)式編程
之前我們已經(jīng)初窺了函數(shù)式編程,知道了它的魅力,現(xiàn)在我們繼續(xù)深入了解一下函數(shù)式編程吧。
其實(shí)函數(shù)我們從小就學(xué),什么一次函數(shù),二次函數(shù)……根據(jù)學(xué)術(shù)上函數(shù)的定義,函數(shù)即是一種描述集合和集合之間的轉(zhuǎn)換關(guān)系,輸入通過(guò)函數(shù)都會(huì)返回有且只有一個(gè)輸出值。
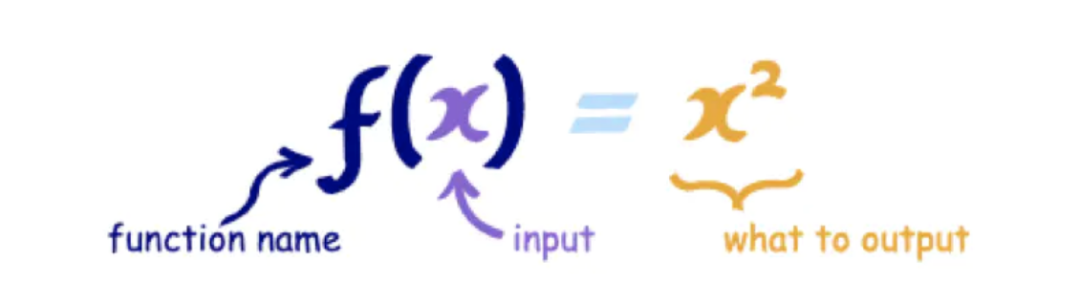
所以,函數(shù)實(shí)際上是一個(gè)關(guān)系,或者說(shuō)是一種映射,而這種映射關(guān)系是可以組合的,一旦我們知道一個(gè)函數(shù)的輸出類型可以匹配另一個(gè)函數(shù)的輸入,那他們就可以進(jìn)行組合。還記得之前寫的 convert2Obj這個(gè)函數(shù):
const convert2Obj = compose(genObj('name'), capitalizeName)
復(fù)制代碼
它實(shí)際上就完成了映射關(guān)系的組合,把一個(gè)數(shù)據(jù)從 String 轉(zhuǎn)換成了 String 然后再轉(zhuǎn)換成 Object。數(shù)學(xué)好的童鞋就知道,這就是數(shù)學(xué)上的復(fù)合運(yùn)算:g°f = g(f(x))
在我們的編程世界中,我們需要處理的其實(shí)也只有“數(shù)據(jù)”和“關(guān)系”,而關(guān)系就是函數(shù)。我們所謂的編程工作也不過(guò)就是在找一種映射關(guān)系,一旦關(guān)系找到了,問(wèn)題就解決了,剩下的事情,就是讓數(shù)據(jù)流過(guò)這種關(guān)系,然后轉(zhuǎn)換成另一個(gè)數(shù)據(jù)罷了。
我特別喜歡用流水線去形容這種工作,把輸入當(dāng)做原料,把輸出當(dāng)做產(chǎn)品,數(shù)據(jù)可以不斷的從一個(gè)函數(shù)的輸出可以流入另一個(gè)函數(shù)輸入,最后再輸出結(jié)果,這不就是一套流水線嘛?
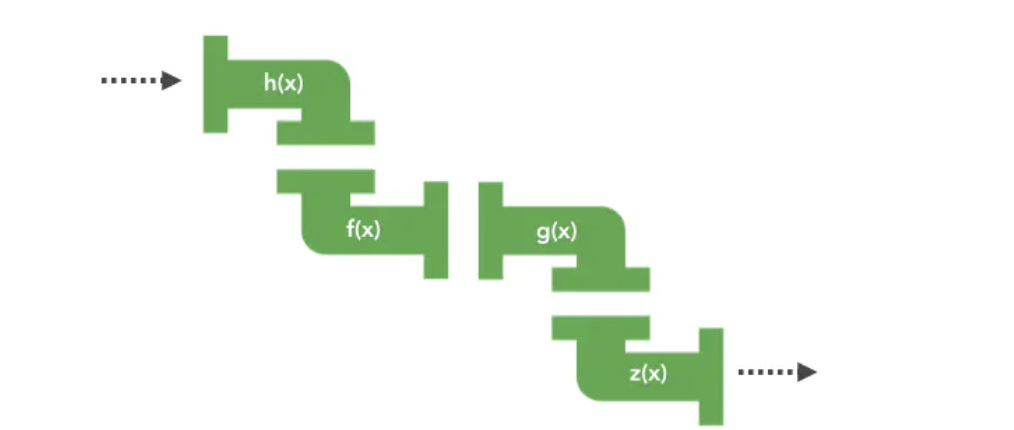
所以,現(xiàn)在你明確了函數(shù)式編程是什么了吧?它其實(shí)就是強(qiáng)調(diào)在編程過(guò)程中把更多的關(guān)注點(diǎn)放在如何去構(gòu)建關(guān)系。通過(guò)構(gòu)建一條高效的建流水線,一次解決所有問(wèn)題。而不是把精力分散在不同的加工廠中來(lái)回奔波傳遞數(shù)據(jù)。
函數(shù)式編程的特點(diǎn)
函數(shù)是“一等公民” (First-Class Functions)
這是函數(shù)式編程得以實(shí)現(xiàn)的前提,因?yàn)槲覀兓镜牟僮鞫际窃诓僮骱瘮?shù)。這個(gè)特性意味著函數(shù)與其他數(shù)據(jù)類型一樣,處于平等地位,可以賦值給其他變量,也可以作為參數(shù),傳入另一個(gè)函數(shù),或者作為別的函數(shù)的返回值,例如前面的
const convert2Obj = compose(genObj('name'), capitalizeName)
復(fù)制代碼
聲明式編程 (Declarative Programming)
通過(guò)上面的例子可以看出來(lái),函數(shù)式編程大多時(shí)候都是在聲明我需要做什么,而非怎么去做。這種編程風(fēng)格稱為 聲明式編程 。這樣有個(gè)好處是代碼的可讀性特別高,因?yàn)槁暶魇酱a大多都是接近自然語(yǔ)言的,同時(shí),它解放了大量的人力,因?yàn)樗魂P(guān)心具體的實(shí)現(xiàn),因此它可以把優(yōu)化能力交給具體的實(shí)現(xiàn),這也方便我們進(jìn)行分工協(xié)作。
SQL 語(yǔ)句就是聲明式的,你無(wú)需關(guān)心 Select 語(yǔ)句是如何實(shí)現(xiàn)的,不同的數(shù)據(jù)庫(kù)會(huì)去實(shí)現(xiàn)它自己的方法并且優(yōu)化。React 也是聲明式的,你只要描述你的 UI,接下來(lái)狀態(tài)變化后 UI 如何更新,是 React 在運(yùn)行時(shí)幫你處理的,而不是靠你自己去渲染和優(yōu)化 diff 算法。
惰性執(zhí)行(Lazy Evaluation)
所謂惰性執(zhí)行指的是函數(shù)只在需要的時(shí)候執(zhí)行,即不產(chǎn)生無(wú)意義的中間變量。像剛才的例子,函數(shù)式編程跟命令式編程最大的區(qū)別就在于幾乎沒(méi)有中間變量,它從頭到尾都在寫函數(shù),只有在最后的時(shí)候才通過(guò)調(diào)用 convertName 產(chǎn)生實(shí)際的結(jié)果。
無(wú)狀態(tài)和數(shù)據(jù)不可變 (Statelessness and Immutable data)
這是函數(shù)式編程的核心概念:
數(shù)據(jù)不可變: 它要求你所有的數(shù)據(jù)都是不可變的,這意味著如果你想修改一個(gè)對(duì)象,那你應(yīng)該創(chuàng)建一個(gè)新的對(duì)象用來(lái)修改,而不是修改已有的對(duì)象。 無(wú)狀態(tài): 主要是強(qiáng)調(diào)對(duì)于一個(gè)函數(shù),不管你何時(shí)運(yùn)行,它都應(yīng)該像第一次運(yùn)行一樣,給定相同的輸入,給出相同的輸出,完全不依賴外部狀態(tài)的變化。
為了實(shí)現(xiàn)這個(gè)目標(biāo),函數(shù)式編程提出函數(shù)應(yīng)該具備的特性:沒(méi)有副作用和純函數(shù)。
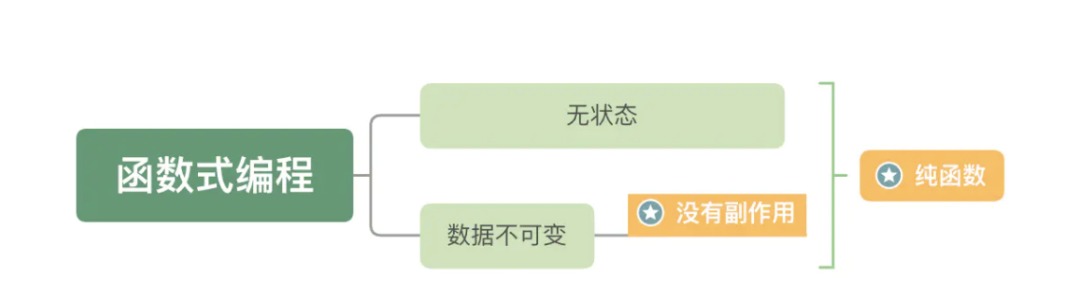
沒(méi)有副作用(No Side Effects)
副作用這個(gè)詞我們可算聽的不少,它的含義是:在完成函數(shù)主要功能之外完成的其他副要功能。在我們函數(shù)中最主要的功能當(dāng)然是根據(jù)輸入返回結(jié)果,而在函數(shù)中我們最常見的副作用就是隨意操縱外部變量。由于 JS 中對(duì)象傳遞的是引用地址,哪怕我們用 const 關(guān)鍵詞聲明對(duì)象,它依舊是可以變的。而正是這個(gè)“漏洞”讓我們有機(jī)會(huì)隨意修改對(duì)象。
例如:map 函數(shù)的本來(lái)功能是將輸入的數(shù)組根據(jù)一個(gè)函數(shù)轉(zhuǎn)換,生成一個(gè)新的數(shù)組:
map :: [a] -> [b]
復(fù)制代碼
而在 JS 中,我們經(jīng)常可以看到下面這種對(duì) map 的 “錯(cuò)誤” 用法,把 map 當(dāng)作一個(gè)循環(huán)語(yǔ)句,然后去直接修改數(shù)組中的值。
const list = [...];
// 修改 list 中的 type 和 age
list.map(item => {
item.type = 1;
item.age++;
})
復(fù)制代碼
這樣函數(shù)最主要的輸出功能沒(méi)有了,變成了直接修改了外部變量,這就是它的副作用。而沒(méi)有副作用的寫法應(yīng)該是:
const list = [...];
// 修改 list 中的 type 和 age
const newList = list.map(item => ({...item, type: 1, age:item.age + 1}));
復(fù)制代碼
保證函數(shù)沒(méi)有副作用,一來(lái)能保證數(shù)據(jù)的不可變性,二來(lái)能避免很多因?yàn)楣蚕頎顟B(tài)帶來(lái)的問(wèn)題。當(dāng)你一個(gè)人維護(hù)代碼時(shí)候可能還不明顯,但隨著項(xiàng)目的迭代,項(xiàng)目參與人數(shù)增加,大家對(duì)同一變量的依賴和引用越來(lái)越多,這種問(wèn)題會(huì)越來(lái)越嚴(yán)重。最終可能連維護(hù)者自己都不清楚變量到底是在哪里被改變而產(chǎn)生 Bug。
傳遞引用一時(shí)爽,代碼重構(gòu)火葬場(chǎng)
純函數(shù) (pure functions)
純函數(shù)算是在 “沒(méi)有副作用” 的要求上再進(jìn)一步了。相信你已經(jīng)在很多地方接觸過(guò)這個(gè)詞,在 Redux 的三大原則中,我們看到,它要求所有的修改必須使用純函數(shù)。
Changes are made with pure functions
其實(shí)純函數(shù)的概念很簡(jiǎn)單就是兩點(diǎn):
不依賴外部狀態(tài)(無(wú)狀態(tài)): 函數(shù)的的運(yùn)行結(jié)果不依賴全局變量,this 指針,IO 操作等。 沒(méi)有副作用(數(shù)據(jù)不變): 不修改全局變量,不修改入?yún)ⅰ?/section>
所以純函數(shù)才是真正意義上的 “函數(shù)”, 它意味著相同的輸入,永遠(yuǎn)會(huì)得到相同的輸出。
以下幾個(gè)函數(shù)都是不純的,因?yàn)樗麄兌家蕾囃獠孔兞浚囅胍幌拢绻腥苏{(diào)用了 changeName 對(duì) curUser 進(jìn)行了修改,然后你在另外的地方調(diào)用了 saySth ,這樣就會(huì)產(chǎn)生你預(yù)料之外的結(jié)果。
const curUser = {
name: 'Peter'
}
const saySth = str => curUser.name + ': ' + str; // 引用了全局變量
const changeName = (obj, name) => obj.name = name; // 修改了輸入?yún)?shù)
changeName(curUser, 'Jay'); // { name: 'Jay' }
saySth('hello!'); // Jay: hello!
復(fù)制代碼
如果改成純函數(shù)的寫法會(huì)是怎么樣呢?
const curUser = {
name: 'Peter'
}
const saySth = (user, str) => user.name + ': ' + str; // 不依賴外部變量
const changeName = (user, name) => ({...user, name }); // 未修改外部變量
const newUser = changeName(curUser, 'Jay'); // { name: 'Jay' }
saySth(curUser, 'hello!'); // Peter: hello!
復(fù)制代碼
這樣就沒(méi)有之前說(shuō)的那些問(wèn)題了。
我們這么強(qiáng)調(diào)使用純函數(shù),純函數(shù)的意義是什么?
便于測(cè)試和優(yōu)化:這個(gè)意義在實(shí)際項(xiàng)目開發(fā)中意義非常大,由于純函數(shù)對(duì)于相同的輸入永遠(yuǎn)會(huì)返回相同的結(jié)果,因此我們可以輕松斷言函數(shù)的執(zhí)行結(jié)果,同時(shí)也可以保證函數(shù)的優(yōu)化不會(huì)影響其他代碼的執(zhí)行。這十分符合測(cè)試驅(qū)動(dòng)開發(fā) TDD(Test-Driven Development )的思想,這樣產(chǎn)生的代碼往往健壯性更強(qiáng)。 可緩存性:因?yàn)橄嗤妮斎肟偸强梢苑祷叵嗤妮敵觯虼耍覀兛梢蕴崆熬彺婧瘮?shù)的執(zhí)行結(jié)果,有很多庫(kù)有所謂的 memoize函數(shù),下面以一個(gè)簡(jiǎn)化版的memoize為例,這個(gè)函數(shù)就能緩存函數(shù)的結(jié)果,對(duì)于像fibonacci這種計(jì)算,就可以起到很好的緩存效果。
function memoize(fn) {
const cache = {};
return function() {
const key = JSON.stringify(arguments);
var value = cache[key];
if(!value) {
value = [fn.apply(null, arguments)]; // 放在一個(gè)數(shù)組中,方便應(yīng)對(duì) undefined,null 等異常情況
cache[key] = value;
}
return value[0];
}
}
const fibonacci = memoize(n => n < 2 ? n: fibonacci(n - 1) + fibonacci(n - 2));
console.log(fibonacci(4)) // 執(zhí)行后緩存了 fibonacci(2), fibonacci(3), fibonacci(4)
console.log(fibonacci(10)) // fibonacci(2), fibonacci(3), fibonacci(4) 的結(jié)果直接從緩存中取出,同時(shí)緩存其他的
復(fù)制代碼
自文檔化:由于純函數(shù)沒(méi)有副作用,所以其依賴很明確,因此更易于觀察和理解(配合后面介紹的 [類型簽名](#hindly-milner 類型簽名)更佳)。 更少的 Bug:使用純函數(shù)意味著你的函數(shù)中不存在指向不明的 this,不存在對(duì)全局變量的引用,不存在對(duì)參數(shù)的修改,這些共享狀態(tài)往往是絕大多數(shù) bug 的源頭。
好了,說(shuō)了這么多,接下來(lái)就讓我們看看在 JS 中如何使用函數(shù)式編程吧。
流水線的構(gòu)建
如果說(shuō)函數(shù)式編程中有兩種操作是必不可少的那無(wú)疑就是柯里化(Currying)**和**函數(shù)組合(Compose),柯里化其實(shí)就是流水線上的加工站,函數(shù)組合就是我們的流水線,它由多個(gè)加工站組成。
接下來(lái),就讓我們看看如何在 JS 中利用函數(shù)式編程的思想去組裝一套高效的流水線。
加工站——柯里化
柯里化的意思是將一個(gè)多元函數(shù),轉(zhuǎn)換成一個(gè)依次調(diào)用的單元函數(shù)。
f(a,b,c) → f(a)(b)(c)
復(fù)制代碼
我們嘗試寫一個(gè) curry 版本的 add 函數(shù)
var add = function(x) {
return function(y) {
return x + y;
};
};
const increment = add(1);
increment(10); // 11
復(fù)制代碼
為什么這個(gè)單元函數(shù)很重要?還記得我們之前說(shuō)過(guò)的,函數(shù)的返回值,有且只有一個(gè)嘛? 如果我們想順利的組裝流水線,那我就必須保證我每個(gè)加工站的輸出剛好能流向下個(gè)工作站的輸入。因此,在流水線上的加工站必須都是單元函數(shù)。
現(xiàn)在很好理解為什么柯里化配合函數(shù)組合有奇效了,因?yàn)榭吕锘幚淼慕Y(jié)果剛好就是單輸入的。
部分函數(shù)應(yīng)用 vs 柯里化
經(jīng)常有人搞不清柯里化和部分函數(shù)應(yīng)用 ( Partial Function Application ),經(jīng)常把他們混為一談,其實(shí)這是不對(duì)的,在維基百科里有明確的定義,部分函數(shù)應(yīng)用強(qiáng)調(diào)的是固定一定的參數(shù),返回一個(gè)更小元的函數(shù)。通過(guò)以下表達(dá)式展示出來(lái)就明顯了:
// 柯里化
f(a,b,c) → f(a)(b)(c)
// 部分函數(shù)調(diào)用
f(a,b,c) → f(a)(b,c) / f(a,b)(c)
復(fù)制代碼
柯里化強(qiáng)調(diào)的是生成單元函數(shù),部分函數(shù)應(yīng)用的強(qiáng)調(diào)的固定任意元參數(shù),而我們平時(shí)生活中常用的其實(shí)是部分函數(shù)應(yīng)用,這樣的好處是可以固定參數(shù),降低函數(shù)通用性,提高函數(shù)的適合用性。
// 假設(shè)一個(gè)通用的請(qǐng)求 API
const request = (type, url, options) => ...
// GET 請(qǐng)求
request('GET', 'http://....')
// POST 請(qǐng)求
request('POST', 'http://....')
// 但是通過(guò)部分調(diào)用后,我們可以抽出特定 type 的 request
const get = request('GET');
get('http://', {..})
復(fù)制代碼
高級(jí)柯里化
通常我們不會(huì)自己去寫 curry 函數(shù),現(xiàn)成的庫(kù)大多都提供了 curry 函數(shù)的實(shí)現(xiàn),但是使用過(guò)的人肯定有會(huì)有疑問(wèn),我們使用的 Lodash,Ramda 這些庫(kù)中實(shí)現(xiàn)的 curry 函數(shù)的行為好像和柯里化不太一樣呢,他們實(shí)現(xiàn)的好像是部分函數(shù)應(yīng)用呢?
const add = R.curry((x, y, z) => x + y + z);
const add7 = add(7);
add7(1,2) // 10
const add1_2 = add(1,2);
add1_2(7) // 10
復(fù)制代碼
其實(shí),這些庫(kù)中的 curry 函數(shù)都做了很多優(yōu)化,導(dǎo)致這些庫(kù)中實(shí)現(xiàn)的柯里化其實(shí)不是純粹的柯里化,我們可以把他們理解為“高級(jí)柯里化”。這些版本實(shí)現(xiàn)可以根據(jù)你輸入的參數(shù)個(gè)數(shù),返回一個(gè)柯里化函數(shù)/結(jié)果值。即,如果你給的參數(shù)個(gè)數(shù)滿足了函數(shù)條件,則返回值。這樣可以解決一個(gè)問(wèn)題,就是如果一個(gè)函數(shù)是多輸入,就可以避免使用 (a)(b)(c) 這種形式傳參了。
所以上面的 add7(1, 2) 能直接輸出結(jié)果不是因?yàn)?nbsp;add(7) 返回了一個(gè)接受 2 個(gè)參數(shù)的函數(shù),而是你剛好傳了 2 個(gè)參數(shù),滿足了所有參數(shù),因此給你計(jì)算了結(jié)果,下面的代碼就很明顯了:
const add = R.curry((x, y, z) => x + y + z);
const add7 = add(7);
add(7)(1) // function
復(fù)制代碼
如果 add7 是一個(gè)接受 2 個(gè)參數(shù)的函數(shù),那么 add7(1) 就不應(yīng)該返回一個(gè) function 而是一個(gè)值了。
因此,記住這句話:我們可以用高級(jí)柯里化去實(shí)現(xiàn)部分函數(shù)應(yīng)用,但是柯里化不等于部分函數(shù)應(yīng)用。
柯里化的應(yīng)用
通常,我們?cè)趯?shí)踐中使用柯里化都是為了把某個(gè)函數(shù)變得單值化,這樣可以增加函數(shù)的多樣性,使得其適用性更強(qiáng):
const replace = curry((a, b, str) => str.replace(a, b));
const replaceSpaceWith = replace(/\s*/);
const replaceSpaceWithComma = replaceSpaceWith(',');
const replaceSpaceWithDash = replaceSpaceWith('-');
復(fù)制代碼
通過(guò)上面這種方式,我們從一個(gè) replace 函數(shù)中產(chǎn)生很多新函數(shù),可以在各種場(chǎng)合進(jìn)行使用。
更重要的是,單值函數(shù)是我們即將講到的函數(shù)組合的基礎(chǔ)。
流水線——函數(shù)組合
上面我們借助 curry,已經(jīng)可以很輕松的構(gòu)造一個(gè)加工站了,現(xiàn)在就是我們組合成流水線的時(shí)候了。
函數(shù)組合概念
函數(shù)組合的目的是將多個(gè)函數(shù)組合成一個(gè)函數(shù)。下面來(lái)看一個(gè)簡(jiǎn)化版的實(shí)現(xiàn):
const compose = (f, g) => x => f(g(x))
const f = x => x + 1;
const g = x => x * 2;
const fg = compose(f, g);
fg(1) //3
復(fù)制代碼
我們可以看到 compose 就實(shí)現(xiàn)了一個(gè)簡(jiǎn)單的功能:形成了一個(gè)全新的函數(shù),而這個(gè)函數(shù)就是一條從 g -> f 的流水線。同時(shí)我們可以很輕易的發(fā)現(xiàn) compose 其實(shí)是滿足結(jié)合律的
compose(f, compose(g, t)) = compose(compose(f, g), t) = f(g(t(x)))
復(fù)制代碼
只要其順序一致,最后的結(jié)果是一致的,因此,我們可以寫個(gè)更高級(jí)的 compose,支持多個(gè)函數(shù)組合:
compose(f, g, t) => x => f(g(t(x))
復(fù)制代碼
簡(jiǎn)單實(shí)現(xiàn)如下:
const compose = (...fns) => (...args) => fns.reduceRight((val, fn) => fn.apply(null, [].concat(val)), args);
const f = x => x + 1;
const g = x => x * 2;
const t = (x, y) => x + y;
let fgt = compose(f, g, t);
fgt(1, 2); // 3 -> 6 -> 7
復(fù)制代碼
函數(shù)組合應(yīng)用
考慮一個(gè)小功能:將數(shù)組最后一個(gè)元素大寫,假設(shè) log, head,reverse,toUpperCase函數(shù)存在(我們通過(guò) curry 可以很容易寫出來(lái))
命令式的寫法:
log(toUpperCase(head(reverse(arr))))
復(fù)制代碼
面向?qū)ο蟮膶懛ǎ?/p>arr.reverse()
.head()
.toUpperCase()
.log()
復(fù)制代碼
鏈?zhǔn)秸{(diào)用看起來(lái)順眼多了,然而問(wèn)題在于,原型鏈上可供我們鏈?zhǔn)秸{(diào)用的函數(shù)是有限的,而需求是無(wú)限的 ,這限制了我們的邏輯表現(xiàn)力。
再看看,現(xiàn)在通過(guò)組合,我們?nèi)绾螌?shí)現(xiàn)之前的功能:
const upperLastItem = compose(log, toUpperCase, head, reverse);
復(fù)制代碼
通過(guò)參數(shù)我們可以很清晰的看出發(fā)生了 uppderLastItem 做了什么,它完成了一套流水線,所有經(jīng)過(guò)這條流水線的參數(shù)都會(huì)經(jīng)歷:reverse -> head -> toUpperCase -> log 這些函數(shù)的加工,最后生成結(jié)果。

最完美的是,這些函數(shù)都是非常簡(jiǎn)單的純函數(shù),你可以隨意組合,隨意拿去用,不用有任何的顧忌。
其實(shí)有些經(jīng)驗(yàn)豐富的程序猿已經(jīng)看出來(lái)一些蹊蹺,這不就是所謂管道 ( pipe ) 的概念嘛?在 Linux 命令中常會(huì)用到,類似ps grep的組合
ps -ef | grep nginx
復(fù)制代碼
只是管道的執(zhí)行方向和 compose (從右往左的組合 ) 好像剛好相反,因此很多函數(shù)庫(kù)(Lodash,Ramda)中也提供了另一種組合方式:pipe(從左往右的組合)
const upperLastItem = R.pipe(reverse, head, toUppderCase, log);
復(fù)制代碼
其實(shí)函數(shù)式編程的理念和 Linux 的設(shè)計(jì)哲學(xué)很像:
有眾多單一目的的小程序,一個(gè)程序只實(shí)現(xiàn)一個(gè)功能,多個(gè)程序組合完成復(fù)雜任務(wù)。
函數(shù)組合的好處
函數(shù)組合的好處顯而易見,它讓代碼變得簡(jiǎn)單而富有可讀性,同時(shí)通過(guò)不同的組合方式,我們可以輕易組合出其他常用函數(shù),讓我們的代碼更具表現(xiàn)力
// 組合方式 1
const last = compose(head, reverse);
const shout = compose(log, toUpperCase);
const shoutLast = compose(shout, last);
// 組合方式 2
const lastUppder = compose(toUpperCase, head, reverse);
const logLastUpper = compose(log, lastUppder);
復(fù)制代碼
這個(gè)過(guò)程,就像搭樂(lè)高積木一樣。
由此可見,大型的程序,都可以通過(guò)這樣一步步的拆分組合實(shí)現(xiàn),而剩下要做的,就是去構(gòu)造足夠多的積木塊(函數(shù))。
實(shí)踐經(jīng)驗(yàn)
在使用柯里化和函數(shù)組合的時(shí)候,有一些經(jīng)驗(yàn)可以借鑒一下:
柯里化中把要操作的數(shù)據(jù)放到最后
因?yàn)槲覀兊妮敵鐾ǔJ切枰僮鞯臄?shù)據(jù),這樣當(dāng)我們固定了之前的參數(shù)(我們可以稱為配置)后,可以變成一個(gè)單元函數(shù),直接被函數(shù)組合使用,這也是其他的函數(shù)式語(yǔ)言遵循的規(guī)范:
const split = curry((x, str) => str.split(x));
const join = curry((x, arr) => arr.join(x));
const replaceSpaceWithComma = compose(join(','), split(' '));
const replaceCommaWithDash = compose(join('-'), split(','));
復(fù)制代碼
但是如果有些函數(shù)沒(méi)遵循這個(gè)約定,我們的函數(shù)該如何組合?當(dāng)然也不是沒(méi)辦法,很多庫(kù)都提供了占位符的概念,例如 Ramda 提供了一個(gè)占位符號(hào)(R.__)。假設(shè)我們的 split 把 str 放在首位
const split = curry((str, x) => str.split(x));
const replaceSpaceWithComma = compose(join(','), split(R.__, ' '));
復(fù)制代碼
函數(shù)組合中函數(shù)要求單輸入
函數(shù)組合有個(gè)使用要點(diǎn),就是中間的函數(shù)一定是單輸入的,這個(gè)很好理解,之前也說(shuō)過(guò)了,因?yàn)楹瘮?shù)的輸出都是單個(gè)的(數(shù)組也只是一個(gè)元素)。
函數(shù)組合的 Debug
當(dāng)遇到函數(shù)出錯(cuò)的時(shí)候怎么辦?我們想知道在哪個(gè)環(huán)節(jié)出錯(cuò)了,這時(shí)候,我們可以借助一個(gè)輔助函數(shù) trace,它會(huì)臨時(shí)輸出當(dāng)前階段的結(jié)果。
const trace = curry((tip, x) => { console.log(tip, x); return x; });
const lastUppder = compose(toUpperCase, head, trace('after reverse'), reverse);
復(fù)制代碼
多參考 Ramda
現(xiàn)有的函數(shù)式編程工具庫(kù)很多,Lodash/fp 也提供了,但是不是很推薦使用 Lodash/fp 的函數(shù)庫(kù),因?yàn)樗暮芏嗪瘮?shù)把需要處理的參數(shù)放在了首位( 例如 map )這不符合我們之前說(shuō)的最佳實(shí)踐。
這里推薦使用 Ramda,它應(yīng)該是目前最符合函數(shù)式編程的工具庫(kù),它里面的所有函數(shù)都是 curry 的,而且需要操作的參數(shù)都是放在最后的。上述的 split,join,replace 這些基本的都在 Ramda 中可以直接使用,它一共提供了 200 多個(gè)超實(shí)用的函數(shù),合理使用可以大大提高你的編程效率(目前我的個(gè)人經(jīng)驗(yàn)來(lái)說(shuō),我需要的功能它 90%都提供了)。
實(shí)戰(zhàn)一下
現(xiàn)在你已經(jīng)基本學(xué)會(huì)了所有的基礎(chǔ)概念,那讓我們來(lái)實(shí)戰(zhàn)一下吧!
假設(shè)我現(xiàn)在有一套數(shù)據(jù):
const data = [
{
name: 'Peter',
sex: 'M',
age: 18,
grade: 99
},
……
]
復(fù)制代碼
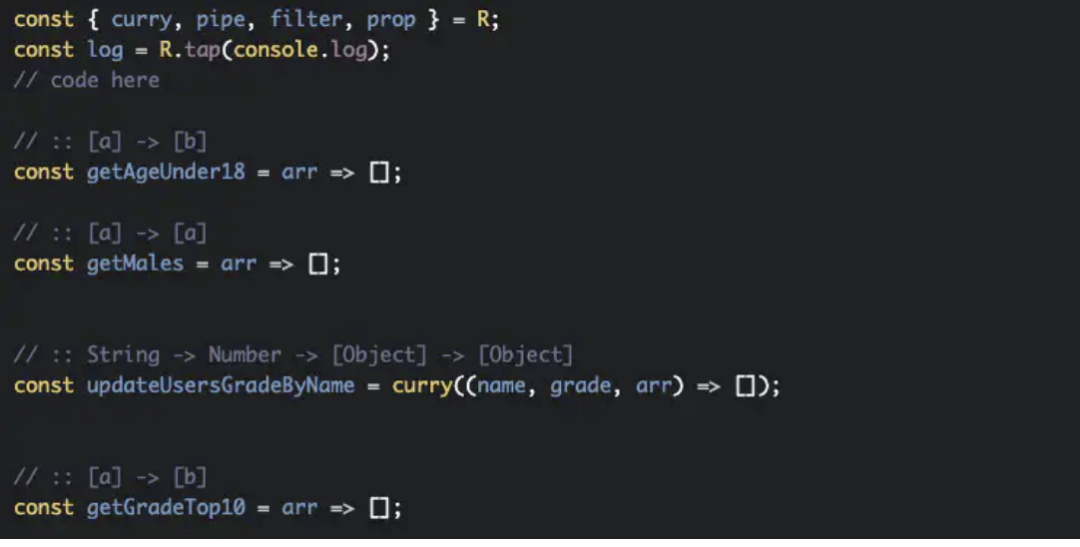
實(shí)現(xiàn)以下幾個(gè)常用功能:
獲取所有年齡小于 18 歲的對(duì)象,并返回他們的名稱和年齡。 查找所有男性用戶。 更新一個(gè)指定名稱用戶的成績(jī)(不影響原數(shù)組)。 取出成績(jī)最高的 10 名,并返回他們的名稱和分?jǐn)?shù)。
我這邊提供以下 Ramda 庫(kù)中的參考函數(shù):
// 對(duì)象操作(最后一個(gè)參數(shù)是對(duì)象),均會(huì)返回新的對(duì)象拷貝
R.prop('name') // 獲取對(duì)象 name 字段的值
R.propEq('name', '123') // 判斷對(duì)象 name 字段是否等于‘123’
R.assoc('name', '123') // 更新對(duì)象的'name'的值為'123'
R.pick(['a', 'd']); //=> {a: 1, d: 4} // 獲取對(duì)象某些屬性,如果對(duì)應(yīng)屬性不存在則不返回
R.pickAll(['a', 'd']); //=> {a: 1, d: 4} // 獲取對(duì)象某些屬性,如果對(duì)應(yīng)屬性不存在則返回`key : undefined`
// 數(shù)組操作
R.map(func) // 傳統(tǒng)的 map 操作
R.filter(func) // 傳統(tǒng)的 filter 操作
R.reject(func) // filter 的補(bǔ)集
R.take(n) // 取出數(shù)組前 n 個(gè)元素
// 比較操作
R.equals(a, b) // 判斷 b 是否等于 a
R.gt(2, 1) => true // 判斷第一個(gè)參數(shù)是否大于第二個(gè)參數(shù)
R.lt(2, 1) => false // 判斷第一個(gè)參數(shù)是否小于第二個(gè)參數(shù)
// 排序操作
R.sort(func) // 根據(jù)某個(gè)排序函數(shù)排序
R.ascend(func) // 根據(jù) func 轉(zhuǎn)換后的值,生成一個(gè)升序比較函數(shù)
R.descend(func) // 根據(jù) func 轉(zhuǎn)換后的值,生成一個(gè)降序比較函數(shù)
// 例子:
R.sort(R.ascend(R.prop('age'))) // 根據(jù) age 進(jìn)行升序排序
// 必備函數(shù)
R.pipe() //compose 的反向,從前往后組合
R.compose() // 從后到前組合
R.curry() // 柯里化
復(fù)制代碼
附錄
Hindly Milner 類型簽名
之前我們遇到了類似這樣的說(shuō)明:
:: String -> Object
復(fù)制代碼
這叫類型簽名,最早是在 Hindley-Milner 類型系統(tǒng)中提出來(lái)的。
你也能在 Ramda 的官網(wǎng)上看到類似的類型簽名:

引入它的好處顯而易見,短短一行,就能暴露函數(shù)的行為和目的,方便我們了解語(yǔ)義。有時(shí)候一個(gè)函數(shù)可能很長(zhǎng),光從代碼上很難理解它到底做了什么:
const replace = reg => sub => str => str.replace(reg, sub);
復(fù)制代碼
而加上類型簽名,我們至少能知道每一步它做了哪些轉(zhuǎn)換,最后輸出一個(gè)什么樣的結(jié)果。
例如這個(gè) replace ,通過(guò)類型簽名我們知道它接受一個(gè) 正則表達(dá) 式和兩個(gè) String,最后會(huì)返回一個(gè) String。
// replace :: Regex -> String -> String -> String
const replace = reg => sub => str => str.replace(reg, sub);
復(fù)制代碼
這樣的連續(xù)箭頭看起來(lái)可能很頭疼,其實(shí)稍微組合一下可以發(fā)現(xiàn),它就是柯里化的意思:先傳一個(gè) 正則表達(dá)式 會(huì)返回一個(gè)函數(shù),如果再傳一個(gè) String,也會(huì)返回函數(shù)……直到你輸入了最后一個(gè) String,就會(huì)返回一個(gè) String 的結(jié)果。
// replace :: Regex -> (String -> (String -> String))
復(fù)制代碼
同時(shí)類型簽名可以避免我們?cè)诤喜⒑瘮?shù)的時(shí)候輸入和輸出的類型不一致。
例如 join 函數(shù)通過(guò)類型簽名很明顯是傳入一個(gè) String 的配置,然后就可以將一個(gè) String 數(shù)組 轉(zhuǎn)換成 String。
// join :: String -> [String] -> String
const join = curry((sep, arr) => arr.join(sep));
復(fù)制代碼
同樣,下面這個(gè)函數(shù),它接受一個(gè) String,然后經(jīng)過(guò) strLen 轉(zhuǎn)換能返回一個(gè) Number。
// strLen :: String -> Number
const strLen = str => str.length();
復(fù)制代碼
那我們很容易知道,以上兩個(gè)函數(shù)完全可以組合,因?yàn)樗麄冚斎牒洼敵鲱愋鸵恢拢ㄟ^(guò)組合我們可以完成一個(gè) String 數(shù)組 到 Number 的流水線。
const joinDash = join('-');
const lengthWithDash = compose(strLen, joinDash);
lengthWithDash(['abc', 'def']); // 7
復(fù)制代碼
當(dāng)然還有時(shí)候你的函數(shù)可能不是接受特定的類型,而只是做一些通用的事情,此時(shí)我們可以用 a, b, c…… 這些來(lái)替代一些通用類型,例如 map ,它傳入一個(gè)可以把 a 轉(zhuǎn)換成 b 的函數(shù),然后把a 數(shù)組 轉(zhuǎn)換成b 數(shù)組。
// map :: (a -> b) -> [a] -> [b]
var map = curry(function(f, xs){
return xs.map(f);
});
// head :: [a] -> a
var head = function(xs){ return xs[0]; }
復(fù)制代碼
現(xiàn)在你就學(xué)會(huì)了類型簽名的使用了,我們推薦你寫的每個(gè)函數(shù)都加上類型簽名,方便他人,方便自己。
Pointfree 編程風(fēng)格
我之前提過(guò)一下 Pointfree 這種編程風(fēng)格,它其實(shí)就是強(qiáng)調(diào)在整個(gè)函數(shù)編寫過(guò)程中不出現(xiàn)參數(shù)(point),而只是通過(guò)函數(shù)的組合生成新的函數(shù),實(shí)際數(shù)據(jù)只需要在最后使用函數(shù)的時(shí)候再傳入即可。
// Pointfree 沒(méi)有出現(xiàn)需要操作的參數(shù)
const upperLastItem = compose(toUpperCase, head, reverse);
// 非 Pointfree 出現(xiàn)了需要操作的參數(shù)
const upperLastItem = arr => {
const reverseArr = arr.reverse();
const head = reverseArr[0];
return head.toUpperCase();
}
復(fù)制代碼
我們?cè)谑褂煤瘮?shù)式編程的時(shí)候,其實(shí)自然就會(huì)形成這種風(fēng)格,它有什么好處呢?
無(wú)需考慮參數(shù)命名:能減輕不少思維負(fù)擔(dān),畢竟參數(shù)命名也是個(gè)很費(fèi)事的過(guò)程。 關(guān)注點(diǎn)集中:你無(wú)需考慮數(shù)據(jù),只需要把所有的注意力集中在轉(zhuǎn)換關(guān)系上。 代碼精簡(jiǎn):可以省去通過(guò)中間變量不斷的去傳遞數(shù)據(jù)的過(guò)程。 可讀性強(qiáng):一眼就可以看出來(lái)數(shù)據(jù)的整個(gè)的轉(zhuǎn)換關(guān)系。
剛開始使用這種編程風(fēng)格肯定會(huì)有很多不適應(yīng),但是當(dāng)你能合理運(yùn)用這種編程風(fēng)格后確實(shí)會(huì)讓代碼更加簡(jiǎn)潔和易于理解了。但是凡事無(wú)絕對(duì),學(xué)了 Pointfree 這種風(fēng)格并不意味著你要強(qiáng)迫自己做到一個(gè)參數(shù)都不能出現(xiàn)(比如很多基礎(chǔ)函數(shù),他們本身的編寫就不是 Pointfree 的),函數(shù)式編程也不是所有場(chǎng)合都完全適用的,具體情況具體分析。
記住,你學(xué)習(xí)各種編程范式的最終目的都是為了讓自己的編碼更加高效,易懂,同時(shí)減少出錯(cuò)概率,不能因?yàn)閷W(xué)了一種編程范式,反而導(dǎo)致自己的編程成本大大增加,這就有點(diǎn)本末倒置了
總結(jié)
前面介紹了很多函數(shù)式編程的概念可以總結(jié)出函數(shù)式編程的優(yōu)點(diǎn):
代碼簡(jiǎn)潔,開發(fā)快速:函數(shù)式編程大量使用函數(shù)的組合,函數(shù)的復(fù)用率很高,減少了代碼的重復(fù),因此程序比較短,開發(fā)速度較快。Paul Graham 在《黑客與畫家》一書中寫道:同樣功能的程序,極端情況下,Lisp 代碼的長(zhǎng)度可能是 C 代碼的二十分之一。 接近自然語(yǔ)言,易于理解:函數(shù)式編程大量使用聲明式代碼,基本都是接近自然語(yǔ)言的,加上它沒(méi)有亂七八糟的循環(huán),判斷的嵌套,因此特別易于理解。 易于"并發(fā)編程":函數(shù)式編程沒(méi)有副作用,所以函數(shù)式編程不需要考慮“死鎖”(Deadlock),所以根本不存在“鎖”線程的問(wèn)題。 更少的出錯(cuò)概率:因?yàn)槊總€(gè)函數(shù)都很小,而且相同輸入永遠(yuǎn)可以得到相同的輸出,因此測(cè)試很簡(jiǎn)單,同時(shí)函數(shù)式編程強(qiáng)調(diào)使用純函數(shù),沒(méi)有副作用,因此也很少出現(xiàn)奇怪的 Bug。
因此,如果用一句話來(lái)形容函數(shù)式編程,應(yīng)該是:Less code, fewer bugs 。因?yàn)閷懙拇a越少,出錯(cuò)的概率就越小。人是最不可靠的,我們應(yīng)該盡量把工作交給計(jì)算機(jī)。
一眼看下來(lái)好像函數(shù)式可以解決所有的問(wèn)題,但是實(shí)際上,函數(shù)式編程也不是什么萬(wàn)能的靈丹妙藥。正因?yàn)楹瘮?shù)式編程有以上特點(diǎn),所以它天生就有以下缺陷:
性能:函數(shù)式編程相對(duì)于指令式編程,性能絕對(duì)是一個(gè)短板,因?yàn)樗鶗?huì)對(duì)一個(gè)方法進(jìn)行過(guò)度包裝,從而產(chǎn)生上下文切換的性能開銷。同時(shí),在 JS 這種非函數(shù)式語(yǔ)言中,函數(shù)式的方式必然會(huì)比直接寫語(yǔ)句指令慢(引擎會(huì)針對(duì)很多指令做特別優(yōu)化)。就拿原生方法 map來(lái)說(shuō),它就要比純循環(huán)語(yǔ)句實(shí)現(xiàn)迭代慢 8 倍。資源占用:在 JS 中為了實(shí)現(xiàn)對(duì)象狀態(tài)的不可變,往往會(huì)創(chuàng)建新的對(duì)象,因此,它對(duì)垃圾回收(Garbage Collection)所產(chǎn)生的壓力遠(yuǎn)遠(yuǎn)超過(guò)其他編程方式。這在某些場(chǎng)合會(huì)產(chǎn)生十分嚴(yán)重的問(wèn)題。 遞歸陷阱:在函數(shù)式編程中,為了實(shí)現(xiàn)迭代,通常會(huì)采用遞歸操作,為了減少遞歸的性能開銷,我們往往會(huì)把遞歸寫成尾遞歸形式,以便讓解析器進(jìn)行優(yōu)化。但是眾所周知,JS 是不支持尾遞歸優(yōu)化的(雖然 ES6 中將尾遞歸優(yōu)化作為了一個(gè)規(guī)范,但是真正實(shí)現(xiàn)的少之又少) ……
因此,在性能要求很嚴(yán)格的場(chǎng)合,函數(shù)式編程其實(shí)并不是太合適的選擇。
但是換種思路想,軟件工程界從來(lái)就沒(méi)有停止過(guò)所謂的銀彈之爭(zhēng),卻也從來(lái)沒(méi)誕生過(guò)什么真正的銀彈,各種編程語(yǔ)言層出不窮,各種框架日新月異,各種編程范式推陳出新,結(jié)果誰(shuí)也沒(méi)有真正的替代誰(shuí)。
學(xué)習(xí)函數(shù)式編程真正的意義在于:讓你意識(shí)到在指令式編程,面向?qū)ο缶幊讨猓€有一種全新的編程思路,一種用函數(shù)的角度去抽象問(wèn)題的思路。學(xué)習(xí)函數(shù)式編程能大大豐富你的武器庫(kù),不然,當(dāng)你手中只有一個(gè)錘子,你看什么都像釘子。
我們完全可以在日常工作中將函數(shù)式編程作為一種輔助手段,在條件允許的前提下,借鑒函數(shù)式編程中的思路,例如:
多使用純函數(shù)減少副作用的影響。 使用柯里化增加函數(shù)適用率。 使用 Pointfree 編程風(fēng)格,減少無(wú)意義的中間變量,讓代碼更且可讀性。
- EOF -
