?LeetCode刷題實戰(zhàn)15題： 三數(shù)之和

算法的重要性，我就不多說了吧，想去大廠，就必須要經(jīng)過基礎(chǔ)知識和業(yè)務(wù)邏輯面試+算法面試。所以，為了提高大家的算法能力，這個公眾號后續(xù)每天帶大家做一道算法題，題目就從LeetCode上面選 ！

今天和大家聊的問題叫做三數(shù)之和?，我們先來看題面：

https://leetcode.com/problems/3sum/

描述

給定一個整數(shù)的數(shù)組，要求尋找當中所有的a，b，c三個數(shù)的組合，使得三個數(shù)的和為0.注意，即使數(shù)組當中的數(shù)有重復(fù)，同一個數(shù)也只能使用一次。

Given an array?nums?of?n?integers, are there elements?a?,?b?,?c?in
nums?such that?a?+?b?+?c?= 0? Find all unique triplets in the array
which gives the sum of zero.

Note:

The solution set must not contain duplicate triplets.

樣例

給定數(shù)組 nums = [-1, 0, 1, 2, -1, -4]，

滿足要求的三元組集合為：
[
??[-1, 0, 1],
??[-1, -1, 2]
]

題解

這道題是之前LeetCode第一題2 Sum的提升版，在之前的題目當中，我們尋找的是和等于某個值的兩個數(shù)的組合。而這里，我們需要找的是三個數(shù)。從表面上來看似乎差別不大，但是實際處理起來要麻煩很多。

? 暴力求解??

我們先理一下思路，從最簡單的方法開始入手。這題最簡單的方法當然就是暴力法，我們已經(jīng)明確了要找的是三個數(shù)的和，既然數(shù)量確定了，就好辦了，我們直接枚舉所有三個數(shù)的組合，然后所有和等于0的組合就是答案。但是這里有一個小問題，當我們找到了答案之后，我們并不能直接返回，因為數(shù)組當中重復(fù)的元素很有可能會導(dǎo)致答案的重復(fù)，我們必須要去掉這些重復(fù)的答案，保證答案當中每一個都是唯一的。

那我們先對原數(shù)組做處理，去除掉其中重復(fù)的元素之后再來尋找答案可不可以呢？

很遺憾，這個想法很好，但是不可行。原因也很簡單，因為答案不能重復(fù)，但是答案里的數(shù)是可以重復(fù)的。

舉個例子，比如數(shù)組是[-1, -1, 2, 0, -2]，那么[-1, -1, 2]是一個答案，如果一開始就出去掉了重復(fù)的-1，那么這個答案顯然就無法構(gòu)成了。唯一的解決方法是用容器來維護答案，保證容器內(nèi)的答案是唯一的，不過這個會帶來額外的時間和空間開銷。

所以，總體看來，暴力枚舉并不是個好方法，復(fù)雜度不低，如果使用C++和Java等語言的話，使用容器也很麻煩。

ret = set()
for i in range(n):    for j in range(i+1, n):        for k in range(j+1, n):            if a[i] + a[j] + a[k] == 0:                ret.add((i, j, k))
return?list(ret)

??利用2 Sum??

還有一個思路是利用之前的2 Sum的解法，在之前的2 Sum問題當中，我們通過巧妙地使用map，來達成了在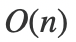復(fù)雜度內(nèi)找到了所有和等于某個值的元素對。所以，我們可以先枚舉第一個數(shù)的大小，然后在剩下的元素當中進行2 Sum操作。

假設(shè)我們枚舉的數(shù)是a[i],那么我們在剩下的元素當中做2 Sum，來尋找和等于-a[i]的兩個數(shù)。最后，將這三個數(shù)組成答案。如果遺忘2 Sum解法的同學(xué)可以點擊下方鏈接回到之前的文章。LeetCode 1 Two Sum——在數(shù)組上遍歷出花樣

這個方法看起來巧妙很多，但是還是逃不掉重復(fù)的問題。舉個例子：[-1, -1, -1, -1, -1, 2]。如果我們枚舉-1，那么會出現(xiàn)多個[-1, -1, 2]的結(jié)果。所以我們依然免不了手動過濾重復(fù)的答案。不過利用2 Sum的解法要比暴力快一些，因為2 Sum的時間復(fù)雜度是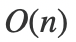，再乘上枚舉元素的復(fù)雜度，不考慮去重情況下的整體復(fù)雜度是O(n^2)，要比枚舉的O(n^3)更優(yōu)。

我們利用2 sum寫出新的算法：

def two_sum(array, idx, target):    """    two sum的部分    """    n = len(array)    ret = []    # 用來記錄所有出現(xiàn)過的元素    appear = set()    # 用來判斷2 sum的答案出現(xiàn)重復(fù)    used = set()    for i in range(idx + 1, n):        # 如果 target - array[i]之前出現(xiàn)過，說明可以構(gòu)成答案        if target - array[i] in appear:            # 判斷答案是否重復(fù)            if array[i] in used or target - array[i] in used:                continue            # 記錄            used.add(array[i])            used.add(target - array[i])            ret.append((array[i], target - array[i]))        appear.add(array[i])    return ret

def three_sum(array):    n = len(array)    # 記錄枚舉過的元素    used = set()    ret = []    # 防止答案重復(fù)    duplicated = set()    for i in range(n):        # 如果出現(xiàn)過，說明已經(jīng)枚舉過，跳過        if array[i] in used:            continue        # 拿到2 sum的答案        combinations = two_sum(array, i, -array[i])        if len(combinations) > 0:            for combination in combinations:                # 組裝答案                answer = tuple(sorted((array[i], *combination)))                # 判斷答案是否重復(fù)                if answer in duplicated:                    continue                # 記錄                ret.append(answer)                duplicated.add(answer)        used.add(array[i])    return ret

? 尺取法??

這題的另一個解法是尺取法，也就是two pointers，也叫做兩指針算法。這個在我們之前的文章當中也有過介紹，有遺忘或者錯過的同學(xué)可以點擊下方的鏈接回顧一下。LeetCode3 一題學(xué)會尺取算法

尺取法的精髓是通過兩個指針控制一個區(qū)間，保證區(qū)間滿足一定的條件。在這題當中，我們要控制的條件其實是三個數(shù)的和。由于我們的指針數(shù)量是2，也就是說我們只有兩個指針，但是我們卻需要找到三個數(shù)組成的答案。顯然，我們直接使用尺取法是不行的。我們稍作變通就可以解決這個問題，就是第一個解法的思路，我們先枚舉一個數(shù)，然后再通過尺取法去尋找另外兩個數(shù)。

使用尺取法需要我們根據(jù)現(xiàn)在區(qū)間內(nèi)的信息，制定策略如何移動區(qū)間。顯然，如果區(qū)間里的數(shù)雜亂無章，我們是很難知道應(yīng)該怎么維護區(qū)間的。所以我們首先對數(shù)組當中的元素進行排序，保證元素的有序性。區(qū)間里的元素有序了，那么我們就方便了。

假設(shè)我們當前枚舉的數(shù)是a[i]，那么我們就需要找到另外的兩個數(shù)b和c，使得b + c = -a[i]。對于每一個i來說，這樣的b和c可能存在，也可能不存在，我們必須要尋找過了才知道。

和2 Sum一樣，為了優(yōu)化時間復(fù)雜度，加快算法的效率，我們需要人為設(shè)置一些限制。我們限制b和c只能在a的右側(cè)，當然也可以限制在一左一右，總之，我們需要把這三個數(shù)的順序固定下來。因為三個數(shù)調(diào)換順序只會產(chǎn)生重復(fù)，所以我們固定順序可以避免重復(fù)。所以我們枚舉a的位置之后，在a的右側(cè)通過尺取法尋找另外兩個元素。

方法也很簡單，我們一開始設(shè)置b的位置是i+1, c的位置是n。如果b+c > -a，那么說明兩者的和過大，因為b已經(jīng)是最小值了，所以只能將c向左移動。如果b+c < -a，說明兩者的和過小，需要增大，所以應(yīng)該將b往右側(cè)移動增大數(shù)值。如此往復(fù)，當這個區(qū)間遍歷完成之后，繼續(xù)移動a的位置，尋找下一組解，這里需要注意，a需要跳過所有重復(fù)的數(shù)字，避免重復(fù)。

我們寫出代碼：

def three_sum(array):    n = len(array)    # 先對array進行排序    array = sorted(array)    ret = []    for i in range(n-2):        # 判斷第一個數(shù)是否重復(fù)        if i > 0 and array[i] == array[i-1]:            continue        used.add(array[i])        # 進行two pointers縮放        j = i + 1        k = n - 1        target = -array[i]        if target < 0:            break        while j < k:            cur_sum = array[j] + array[k]            # 判斷當前區(qū)間的結(jié)果和目標的大小            if cur_sum < target:                    j += 1                continue            elif cur_sum > target:                k -= 1                continue            # 記錄            ret.append(answer)            # 繼續(xù)縮放區(qū)間，尋找其他可能的答案            j += 1            while j < k and array[j] == array[j-1]:                j += 1            k -= 1            while j < k-1 and array[k] == array[k+1]:                k -= 1    return ret

寫出代碼之后，我們來分析一下算法的復(fù)雜度。一開始的時候，我們對數(shù)組進行排序，眾所周知，排序的復(fù)雜度是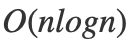。之后，我們枚舉了第一個數(shù)，開銷是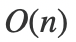，我們進行區(qū)間縮放的復(fù)雜度也是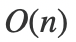，所以整個主體程序的復(fù)雜度是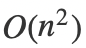。看似和上面一種方法區(qū)別不大，但是我們節(jié)省了set重復(fù)的判斷，由于hashset讀取會有時間開銷，所以雖然算法的量級上沒什么差別，但是常數(shù)更小，真正運行起來這種算法要快很多。

這題官方給的難度是Medium，但實際上我覺得比一般的Medium要難上一些，代碼量也要大上一些。今天文章當中列舉的并不是全部的解法，其他的做法還有很多，比如對所有數(shù)進行分類，分成負數(shù)、零和正數(shù)，然后再進行組裝等等。感興趣的同學(xué)可以自己思考，看看還有沒有其他比較有趣的方法。

今天的文章就到這里，如果覺得有所收獲，請順手點個在看或者轉(zhuǎn)發(fā)吧，你們的支持是我最大的動力。