【建議收藏】面試官會問的位運算奇淫技巧
往期熱門文章:
2、IDEA 2021首個大版本發(fā)布,新增了這幾個超實用功能!
前言
認識位運算
程序中的所有數(shù)在計算機內存中都是以二進制的形式儲存的。位運算就是直接對整數(shù)在內存中的二進制位進行操作。
0&0=0,0&1=0,1&1=1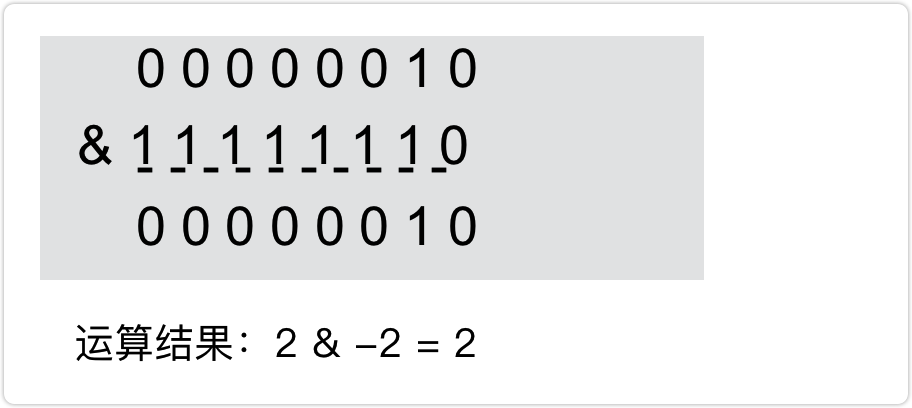
0|0=0,0|1=1,1|1=1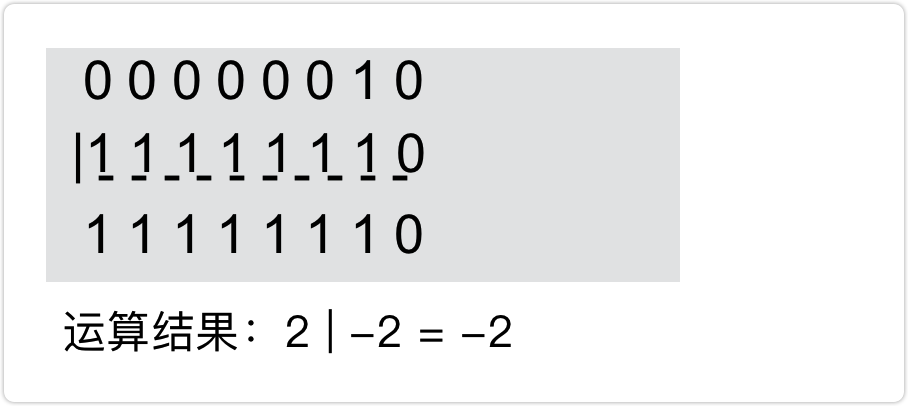
0^0=0, 0^1=1, 1^1=0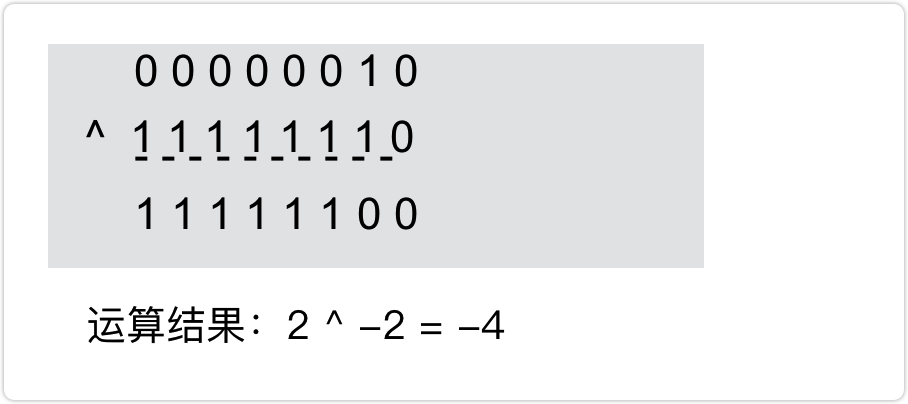
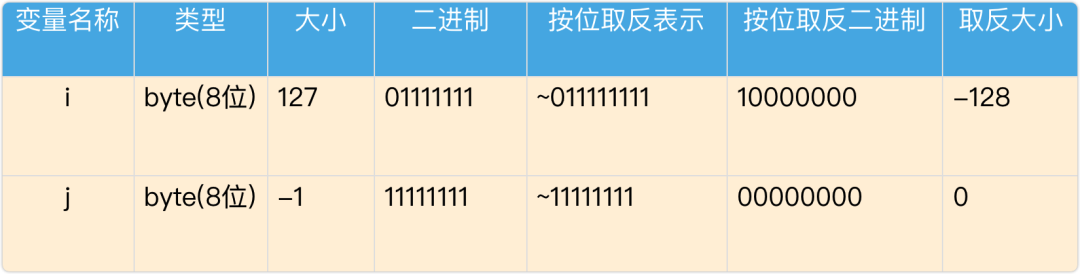
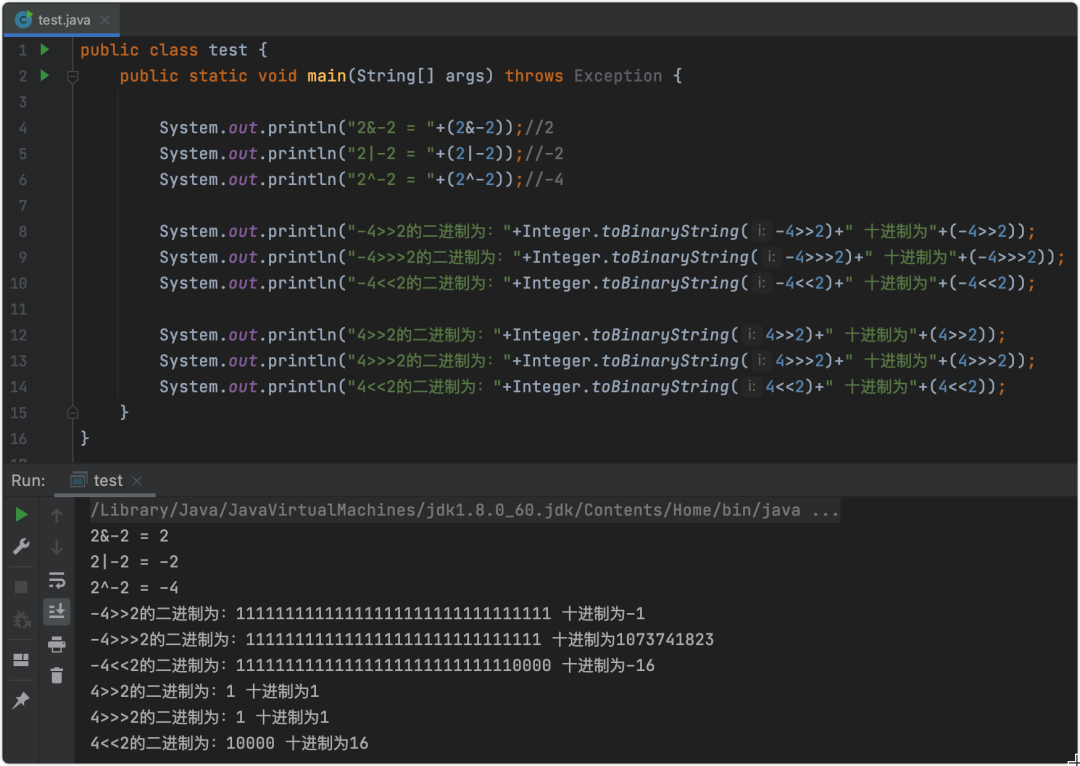
<<:左移后右邊位補 0>>:右移后左邊位補原最左位值(可能是0,可能是1)>>>:右移后左邊位補 0對于左移運算符
<<沒有懸念右側填個零無論正負數(shù)相當于整個數(shù)乘以2。而右移運算符就有分歧了,分別是左側補0
>>>和左側補原始位>>,如果是正數(shù)沒爭議左側都是補0,達到除以2的效果;如果是負數(shù)的話左側補0>>>那么數(shù)值的正負會發(fā)生改變,會從一個負數(shù)變成一個相對較大的正數(shù)。而如果是左側補原始位(負數(shù)補1)>>那么整個數(shù)還是負數(shù),也就是相當于除以2的效果。

位運算小技巧
判斷奇偶數(shù)
if( n % 2 == 1)
// n 是個奇數(shù)
}
if(n & 1 == 1){
// n 是個奇數(shù)。
}
交換兩個數(shù)
int team = a;
a = b;
b = team;
a=a^b;//a=a^b
b=a^b;//b=(a^b)^b=a^0=a
a=a^b;//a=(a^b)^(a^b^b)=0^b=0
二進制枚舉
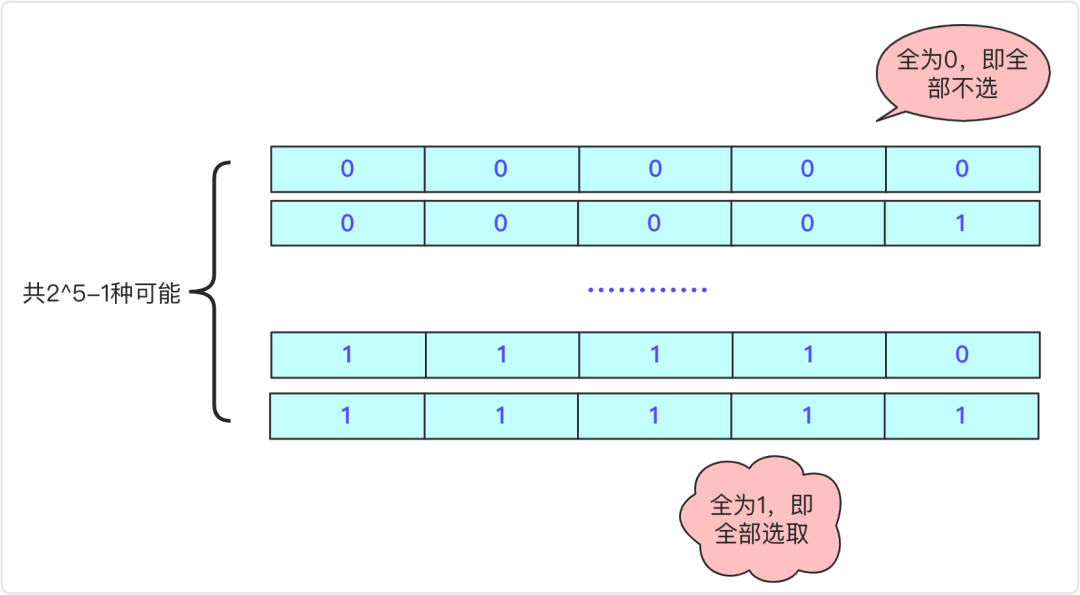
for(int i = 0; i < (1<<n); i++) //從0~2^n-1個狀態(tài)
{
for(int j = 0; j < n; j++) //遍歷二進制的每一位 共n位
{
if(i & (1 << j))//判斷二進制數(shù)字i的第j位是否存在
{
//操作或者輸出
}
}
}
位運算經典問題
不用加減乘除做加法
寫一個函數(shù),求兩個整數(shù)之和,要求在函數(shù)體內不得使用+、-、*、/四則運算符號。
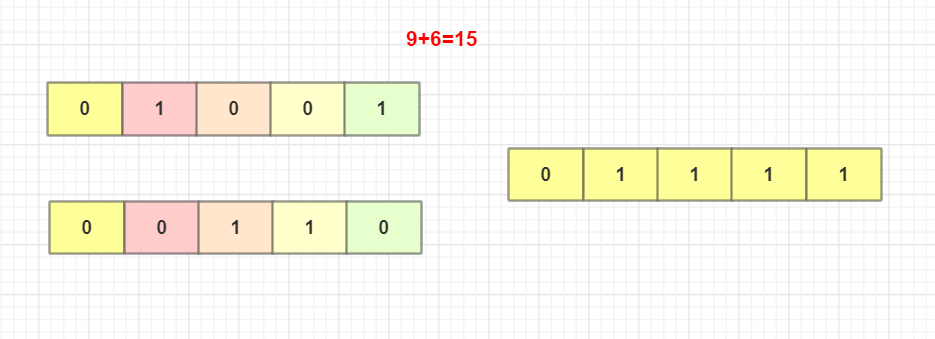 但事實肯定有進位的運算啊!看到上面操作的不足之后,我們肯定還需要解決進位的問題對于進位的兩數(shù)相加,這種核心思想為:
但事實肯定有進位的運算啊!看到上面操作的不足之后,我們肯定還需要解決進位的問題對于進位的兩數(shù)相加,這種核心思想為:用兩個數(shù),一個正常m相加(不考慮進位的)。用異或a^b就是滿足這種要求,先不考慮進位(如果沒進位那么就是最終結果)。另一個專門考慮進位的n。兩個1需要進位。所以我們用a&b與記錄需要進位的。但是還有個問題,進位的要往上面進位,所以就變成這個需要進位的數(shù)左移一位。 然后就變成m+n重新迭代開始上面直到不需要進位的(即n=0時候)。
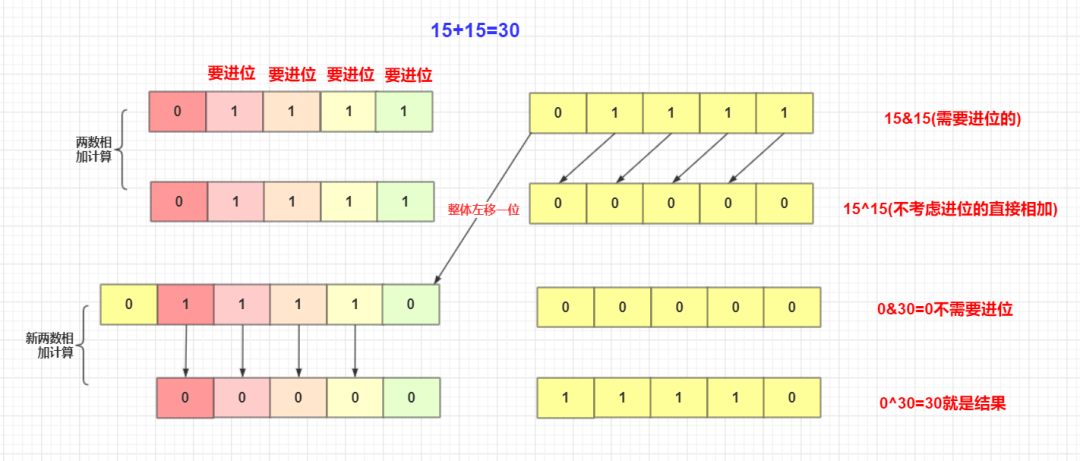
public class Solution {
public int Add(int num1,int num2) {
/*
* 5+3 5^3(0110) 5&3(0001)
* 0101
* 0011
*/
int a=num1^num2;
int b=num1&num2;
b=b<<1;
if(b==0)return a;
else {
return Add(a, b);
}
}
}
二進制中1的個數(shù)

&與。兩個十進制與運算.每一位同1為1。所以我們用2的正數(shù)次冪與知道的數(shù)分別進行與運算操作。如果結果不為0,那么就說明這位為1.(前面31個都是大于0的最后一個與結果是負數(shù)但是如果該位為1那么結果肯定不為0)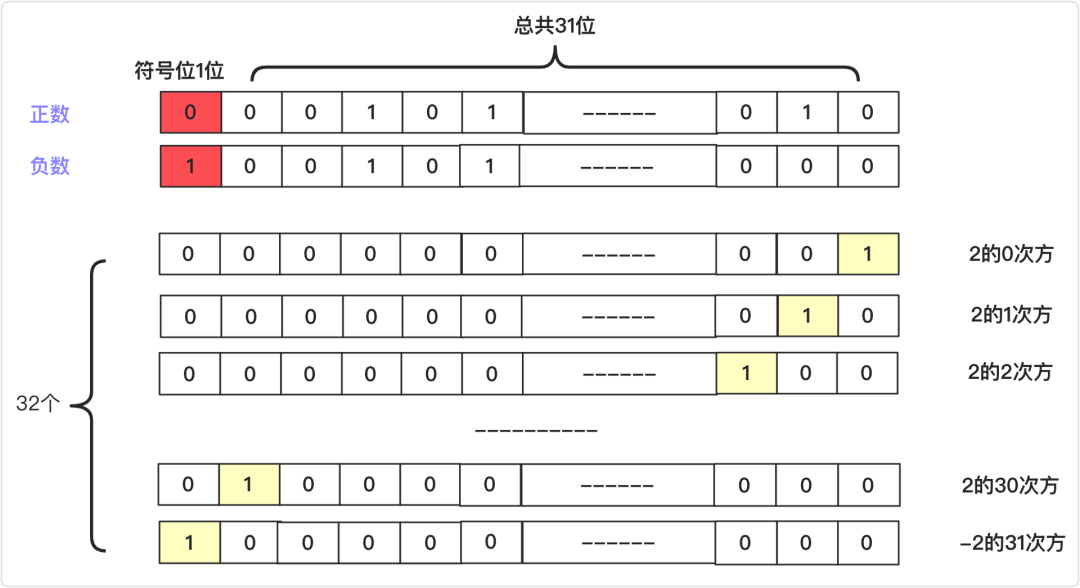
public int NumberOf1(int n) {
int va=0;
for(int i=0;i<32;i++)
{
if((n&(1<<i))!=0)
{
va++;
}
}
return va;
}
n&(n-1)。n如果不為0,那么n-1就是二進制第一個為1的變?yōu)?,后面全為1.這樣的n&(n-1)一次運算就相當于把最后一個1變成0.這樣一直到運算的數(shù)為0停止計算次數(shù)就好了,如下圖共進行三次運算那么n的二進制中就有三個1。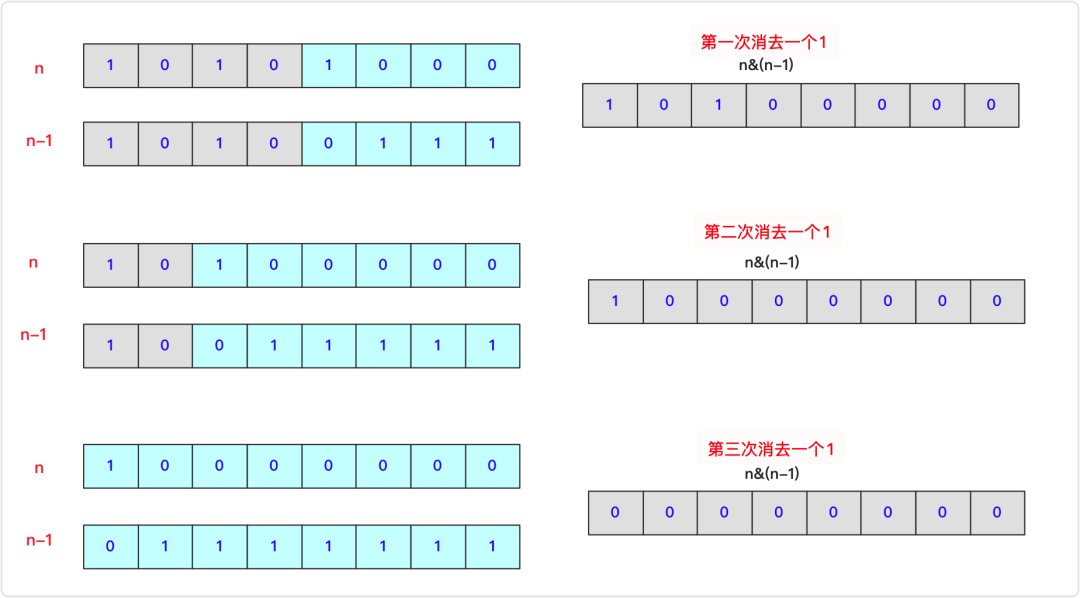
public class Solution {
public int NumberOf1(int n) {
int count=0;
while (n!=0) {
n=n&(n-1);
count++;
}
return count;
}
}
只出現(xiàn)一次的(一個)數(shù)字①
給定一個非空整數(shù)數(shù)組,除了某個元素只出現(xiàn)一次以外,其余每個元素均出現(xiàn)兩次。找出那個只出現(xiàn)了一次的元素。 說明:你的算法應該具有線性時間復雜度。你可以不使用額外空間來實現(xiàn)嗎?
0和任意數(shù)字進行異或操作結果為數(shù)字本身. 兩個相同的數(shù)字進行異或的結果為0.
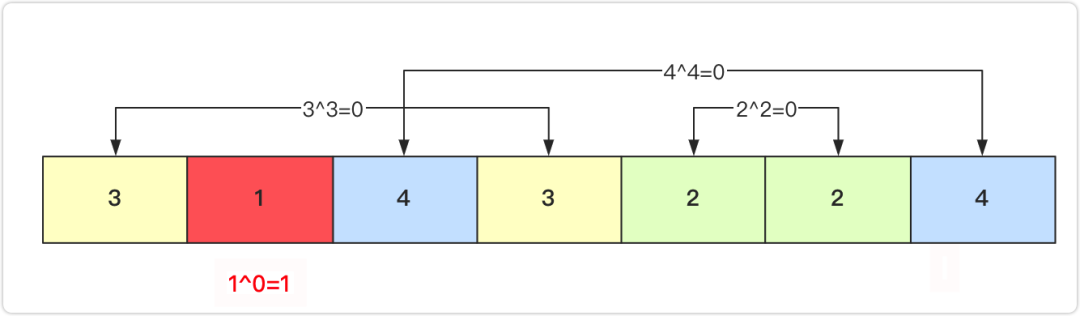
class Solution {
public int singleNumber(int[] nums) {
int value=0;
for(int i=0;i<nums.length;i++)
{
value^=nums[i];
}
return value;
}
}
只出現(xiàn)一次的(一個)數(shù)字②
給定一個非空整數(shù)數(shù)組,除了某個元素只出現(xiàn)一次以外,其余每個元素均出現(xiàn)了三次。找出那個只出現(xiàn)了一次的元素。 說明:你的算法應該具有線性時間復雜度。你可以不使用額外空間來實現(xiàn)嗎?
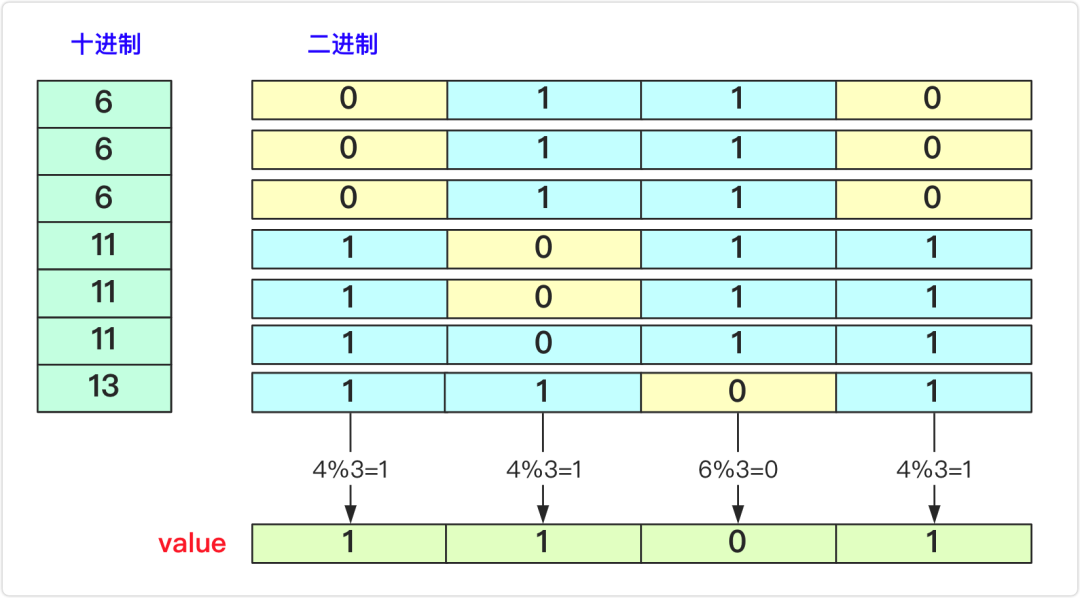
class Solution {
public int singleNumber(int[] nums) {
int value=0;
for(int i=0;i<32;i++)
{
int sum=0;
for(int num:nums)
{
if(((num>>i)&1)==1)
{
sum++;
}
}
if(sum%3==1)
value+=(1<<i);
}
return value;
}
}
只出現(xiàn)一次的(兩個)數(shù)字③
一個整型數(shù)組里除了兩個數(shù)字之外,其他的數(shù)字都出現(xiàn)了兩次。請寫程序找出這兩個只出現(xiàn)一次的數(shù)字。
^。a^b(假設兩個數(shù)值分別為a和b)的值。在看異或^的屬性:不同為1,相同為0. 也就是說最終這個結果的二進制為1的位置上a和b是不相同的。而我們可以找到這個第一個不同的位,然后將數(shù)組中的數(shù)分成兩份,該位為0的進行異或求解得到其中一個結果a,該位為1的進行異或求解得到另一個結果b。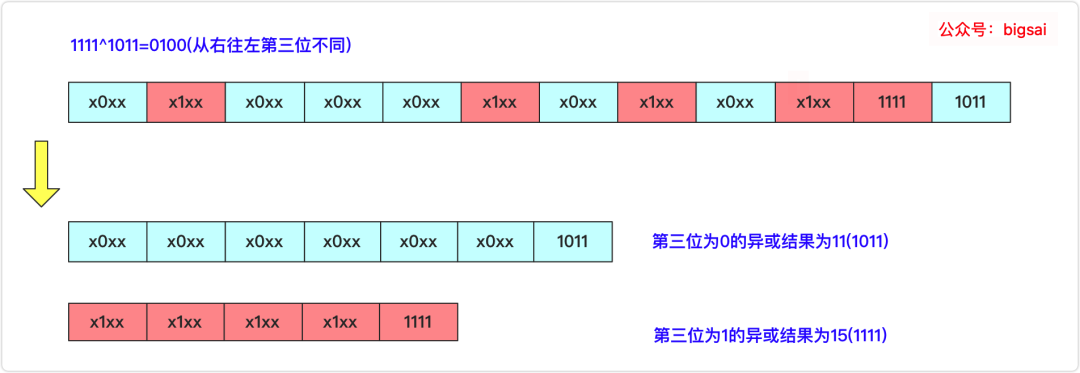
public int[] singleNumbers(int[] nums) {
int value[]=new int[2];
if(nums.length==2)
return nums;
int val=0;//異或求的值
for(int i=0;i<nums.length;i++)
{
val^=nums[i];
}
int index=getFirst1(val);
int num1=0,num2=0;
for(int i=0;i<nums.length;i++)
{
if(((nums[i]>>index)&1)==0)//如果這個數(shù)第index為0 和num1異或
num1^=nums[i];
else//否則和 num2 異或
num2^=nums[i];
}
value[0]=num1;
value[1]=num2;
return value;
}
private int getFirst1(int val) {
int index=0;
while (((val&1)==0&&index<32))
{
val>>=1;// val=val/2
index++;
}
return index;
}
結語
往期熱門文章:
1、《歷史文章分類導讀列表!精選優(yōu)秀博文都在這里了!》
2、七種方式教你在Spring Boot初始化時搞點事情
3、ConcurrentHashMap有十個提升性能的地方,你都知道嗎? 4、程序員等級圖鑒 5、Java 中的 Switch 都支持 String 了,為什么不支持 long? 6、為什么數(shù)據(jù)庫字段要使用NOT NULL? 7、CTO 說了,用錯 @Autowired 和 @Resource 的人可以領盒飯了 8、程序員離職事件始末
9、別總寫代碼,這130個網站比漲工資都重要 10、程序員養(yǎng)生指北
評論
圖片
表情
