重溫斐波那契數(shù)列,再看時(shí)間復(fù)雜度的重要性
? 開題引入斐波那契
? 代碼演示:遞歸、循環(huán)
? 遞歸 vs 循環(huán)
? 時(shí)間復(fù)雜復(fù)高,指數(shù)型O(2^n);推導(dǎo)過程
? 占用線程堆棧, 可能導(dǎo)致棧滿異常
? 壓測(cè)演示
?
打入門軟件開發(fā),斐波那契數(shù)列便是繞不過去的簡(jiǎn)單編程算法。
一個(gè)老生常談的思路是遞歸,另外是循環(huán),今天借此機(jī)會(huì)回顧并演示時(shí)間復(fù)雜度在編程中的重要性。
斐波那契 遞歸算法 1,1,2,3,5,8,13,21,34,55
遞歸算法的應(yīng)用場(chǎng)景是:
? 將大規(guī)模問題,拆解成幾個(gè)小規(guī)模的同樣問題
? 拆解具備終止場(chǎng)景
func Fibonacci(n int) (r int) {
if n == 1 || n == 2 {
r = 1
return
} else {
return Fibonacci(n-1) + Fibonacci(n-2)
}
}為什么能想到循環(huán), 斐波那契數(shù)組也有循環(huán)的含義:
第n個(gè)數(shù)字是循環(huán)指針i從第1個(gè)數(shù)字移動(dòng)到第n-2個(gè)數(shù)字時(shí), 第n-2個(gè)數(shù)字pre和第n-1個(gè)數(shù)字next的和。
func Fibonacci2(n int) (r int) {
if n==1 || n==2 {
return 1
}
pre,next int :=1,1
for i:=0; i<=n-1-2; i++ {
tmp:= pre+next
pre = next
next = tmp
}
}單元測(cè)試如下:
func TestFibonacci(t *testing.T) {
t.Logf("Fibonacci(1) = %d, Fibonacci2(1)= %d ", Fibonacci(1), Fibonacci2(1))
t.Logf("Fibonacci(3) = %d, Fibonacci2(3)= %d ", Fibonacci(3), Fibonacci2(3))
t.Logf("Fibonacci(8) = %d, Fibonacci2(8)= %d ", Fibonacci(8), Fibonacci2(8))
}
go test ./ -v
=== RUN TestFibonacci
m_test.go:8: Fibonacci(1) = 1, Fibonacci2(1)= 1
m_test.go:9: Fibonacci(3) = 2, Fibonacci2(3)= 2
m_test.go:10: Fibonacci(8) = 21, Fibonacci2(8)= 21
--- PASS: TestFibonacci (0.00s)
PASS
ok example.github.com/test 3.359s遞歸的問題在于:
(1) 函數(shù)調(diào)用存在壓棧過程,會(huì)在線程棧(一般2M)上留下棧幀,斐波那契遞歸算法:是函數(shù)自己調(diào)用自己,在終止條件后棧幀開始收斂,但是在此之前有可能已經(jīng)撐爆線程棧。
棧幀中維持著函數(shù)調(diào)用所需要的各種信息,包括函數(shù)的入?yún)ⅰ⒑瘮?shù)的局部變量、函數(shù)執(zhí)行完成后下一步要執(zhí)行的指令地址、寄存器信息等。
(2) 斐波那契遞歸調(diào)用存在重復(fù)計(jì)算,時(shí)間復(fù)雜度是O(2^n),隨著n的增加,需要計(jì)算的次數(shù)陡然增大(業(yè)內(nèi)稱為指數(shù)型變化)。
f(n) = f(n-1)+f(n-2) // 1次計(jì)算
= f(n-2)+f(n-3)+f(n-3)+f(n-4) // 3次計(jì)算
= f(n-3)+f(n-4)+f(n-4)+f(n-5)+f(n-4)+f(n-5)+f(n-5)+f(n-6) // 7次計(jì)算 // 7次計(jì)算
=......
= f(1)+...... // 2^n-1次計(jì)算
故為斐波那契遞歸時(shí)間復(fù)雜度為 O(2^n) 而我們的循環(huán)算法不存在以上問題, 第n個(gè)數(shù)字需要n -2次計(jì)算, 時(shí)間復(fù)雜度是O(n)
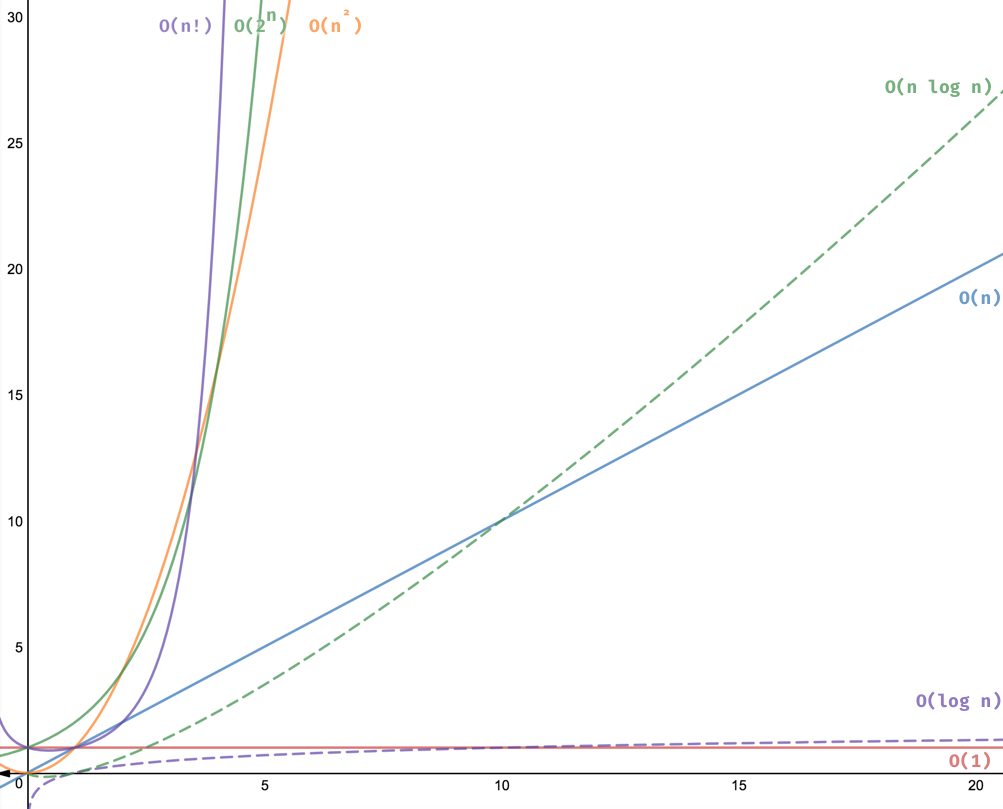
有些童鞋可能沒意識(shí)到指數(shù)型的威力,舉個(gè)例子, 斐波那契遞歸算法,第20個(gè)數(shù)字需要2^20次運(yùn)算;循環(huán)算法只要18次運(yùn)算。
使用基準(zhǔn)測(cè)試壓測(cè):
func BenchmarkF1(b *testing.B) {
for i := 1; i < b.N; i++ {
Fibonacci(20) // 時(shí)間復(fù)雜度 O(2^n)
}
}
func BenchmarkF2(b *testing.B) {
for i := 1; i < b.N; i++ {
Fibonacci2(20) // 時(shí)間復(fù)雜度 O(n)
}
}
go test -bench=. -benchmem ./
goos: darwin
goarch: amd64
pkg: example.github.com/test
cpu: Intel(R) Core(TM) i5-8257U CPU @ 1.40GHz
BenchmarkF1-8 55039 20740 ns/op 0 B/op 0 allocs/op
BenchmarkF2-8 196663548 6.080 ns/op 0 B/op 0 allocs/op
PASS
ok example.github.com/test 3.744s單次執(zhí)行效率(ns/op指標(biāo))相形見絀,甚至斐波那契遞歸n>50+ 不一定能計(jì)算出來。
ok, that'all. 本次快速記錄了遞歸算法相比循環(huán)的兩點(diǎn)劣勢(shì),這里面很重要的常見時(shí)間復(fù)雜度變化曲線[1], 需要程序員必知必會(huì)。https://adrianmejia.com/most-popular-algorithms-time-complexity-every-programmer-should-know-free-online-tutorial-course/
全文原創(chuàng),見字如面,若有不同見解或發(fā)散思維,文末可留言或直接微信噴我。
引用鏈接
[1] 常見時(shí)間復(fù)雜度變化曲線: https://adrianmejia.com/most-popular-algorithms-time-complexity-every-programmer-should-know-free-online-tutorial-course/

流量調(diào)度、微服務(wù)可尋址性和注冊(cè)中心
摸魚快報(bào):golang net/http中的雕蟲小技
點(diǎn)“贊” 戳“在看”
戳“在看” ?
?
