熵

"聊聊熵"

AI-CODE??|??作者?/?AI-code

這是人類之奴公眾號的第58篇原創(chuàng)文章

"熵"在多個學(xué)科中都是一個非常重要的概率，今天我們要探討的是信息論中的"熵"。

在探討"熵"之前，我們先來了解一些預(yù)備知識點：

"信息"，"信息量"

"信息"的一種科學(xué)性定義為：信息是被消除的不確定性。

"太陽從東方升起"，這就不是一條信息。

因為"太陽從東方升起"這是人皆盡知的一件事，它并沒有消除不確定性。

但判斷一句話是否傳達(dá)了信息，這也是一個人類主觀看待的一個問題。

"太陽是太陽系的中心"對于我們當(dāng)代人來說不是一條信息。

但對于哥白尼時代及其以前時代的人來說，卻是信息量巨大的一句話。

要將"信息"這個科學(xué)概率運用于計算機科學(xué)中，就必須尋找到一種非常合適的信息量化指標(biāo)，因為計算機科學(xué)是一門數(shù)字科學(xué)。

"信息量"就是對"信息"數(shù)量大小的衡量指標(biāo)，它的數(shù)學(xué)表達(dá)式為：

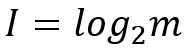
其中m為可能情況的數(shù)量，比如中國乒乓球隊與日本乒乓球隊進(jìn)行比賽，那么比賽的結(jié)果就只有兩種情況：中國乒乓球隊勝、日本乒乓球隊勝。

該事件對應(yīng)的m便為2，帶入上式可知該事件的信息量為1，單位為比特。

判斷一個數(shù)學(xué)表達(dá)式的好壞，可以通過實例來看它是否符合我們的直覺。

對于中國乒乓球隊與日本乒乓球隊的比賽，我們的直覺告訴我們中國乒乓球隊?wèi)?zhàn)勝日本乒乓球隊是毫無懸念的，而信息量又是指消除不確定性的定量衡量，所以這不應(yīng)該是信息量為0嗎？

這種質(zhì)疑是合理的，上述信息量的表達(dá)式只有在所有可能發(fā)生事件的發(fā)生可能性均等的情況下使用才是最合適的。

日常生活中極少發(fā)生的事件一旦發(fā)生，是非常引人注目的；而司空見慣的事件卻很少人會去關(guān)注。

因此，極少見事件攜帶的信息量巨大，即事物出現(xiàn)的概率越小，信息量越大；事物出現(xiàn)的概率越大，信息量越小。

因此，信息量用下式來計算更合適：

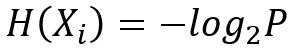
上式P表示事件Xi發(fā)生的先驗概率，所謂先驗概率，就是這個事件按照常理，按照一般性規(guī)律發(fā)生的概率。

在掌握了"信息"、"信息量"這兩個概率后，我們再來揭秘"熵"。

"熵"在信息科學(xué)中可以表達(dá)為信息雜亂程度的量化描述，其數(shù)學(xué)表達(dá)式為：

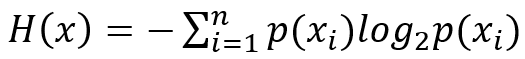
從上述表達(dá)式，我們發(fā)現(xiàn)"熵"為各個事件發(fā)生的概率乘以各自的信息量，然后各項加和。

通過計算，我們發(fā)現(xiàn)熵具有以下規(guī)律：

信息越確定、越單一，熵越小；

信息越不確定、越混亂，熵越大。

對于"熵"計算機科學(xué)中的運用，我們要把握住"熵是度量信息混亂程度的量"這句話。