干貨 | 數(shù)據(jù)結(jié)構(gòu)之圖論基礎
前言
一個好的程序=算法+數(shù)據(jù)結(jié)構(gòu)
數(shù)據(jù)結(jié)構(gòu)是程序的核心之一,可惜本公眾內(nèi)關(guān)于數(shù)據(jù)結(jié)構(gòu)的文章略顯不足,于是何小編打算與向柯瑋小編一起把數(shù)據(jù)結(jié)構(gòu)這部分補齊,來滿足各位觀眾大老爺。
圖的儲存
鄰接矩陣
首先我們先來介紹一下圖的基本存儲方式,同時也是最簡單容易的圖(ADT)的實現(xiàn)方式。本質(zhì)使用二維數(shù)列A[n][n]表示由n個頂點構(gòu)成的圖,其中每個單元,各自負責描述一對頂點之間可能存在的鄰接關(guān)系,故此得名。
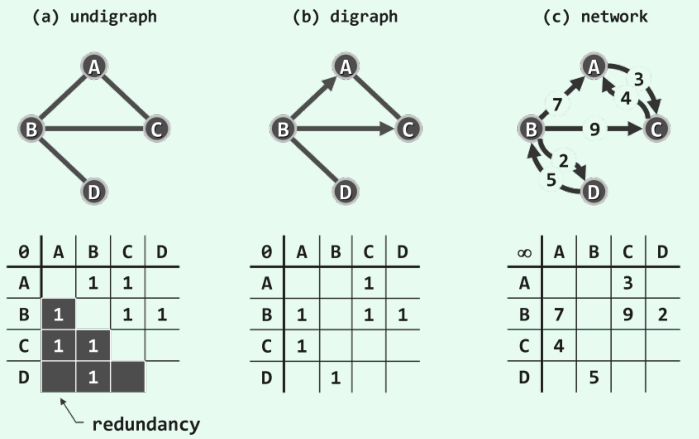
若圖為無權(quán)圖,則A[i][j]聯(lián)通的情況下賦值為1。下圖中的a和b分別為無向圖和有向圖的鄰接矩陣的樣例,對于不存在的邊可以賦值為無窮或0。
下為其C++代碼
/*鄰接矩陣存儲表示*//*MAXNum為定義的最多點數(shù)以下都為此義*/typedef struct GraphMatrix{int isDiGraph;char vexs[MAXNum]; //頂點表int arcs[MAXNum][MAXNum]; //鄰接矩陣int vexnum, arcnum; //當前的頂點數(shù)和邊數(shù)};/*找到頂點v的對應下標*/int LocateVex(GraphMatrix& G, char v){int i;for (i = 0; i < G.vexnum; i++)if (G.vexs[i] == v)return i;}/*采用鄰接矩陣表示法,創(chuàng)建無向圖G*/void Create(GraphMatrix& G){int i, j, k, w;char v1, v2;cin >> G.isDiGraph >> G.vexnum >> G.arcnum; //輸入總頂點數(shù),總邊數(shù)for (i = 0; i < G.vexnum; i++)cin >> G.vexs[i]; //依次輸入點的信息for (i = 0; i < G.vexnum; i++)for (j = 0; j < G.vexnum; j++)G.arcs[i][j] = 0; //初始化鄰接矩陣邊,0表示頂點i和j之間無邊for (k = 0; k < G.arcnum; k++){cin >> v1 >> v2>> w; //輸入一條邊依附的頂點i = LocateVex(G, v1); //找到頂點i的下標j = LocateVex(G, v2); //找到頂點j的下標G.arcs[i][j] = w;if(!G.isDiGraph)G.arcs[i][j] = G.arcs[j][i] = 1; //1表示頂點i和j之間有邊,無向圖不區(qū)分方向}}

性能分析
時間和空間性能分析
時間性能:
依據(jù)上面的代碼分析,當進行靜態(tài)操作時由于向量“循秩訪問”的特長與優(yōu)勢,操作均需O(1)時間。然而在頂點的動態(tài)操作上面卻很耗時。為了插入新的頂點,頂點集向量V[]需要添加一個元素;邊集向量E[][]也需要增加一行,且每行都需要添加一個元素,刪除也是一樣,單次操作的耗時為O(n)。這也是這種向量結(jié)構(gòu)的不足。
空間性能:
上述實現(xiàn)方式所用空間,主要消耗于鄰接矩陣,即其中的二維邊集向量E[][]。由于Vector結(jié)構(gòu)的裝填因子始終不低于50%,故空間總量漸進地不超過O(n ? n) = O(n^2)。
當然對于無相圖,無向圖的鄰接矩陣必為對稱矩陣。每條邊都被儲存了兩篇,接近一半的空間被浪費了,因此可以通過壓縮儲存的方法來提高空間性能。
圖的實現(xiàn)的進一步優(yōu)化
鄰接表
就其有向圖的實現(xiàn),其O(n^2)的空間還有極大的優(yōu)化余地,此方法雖然可以存儲所有的邊,但是對于稀疏圖來說,很多單元對應的邊事實上并未體現(xiàn)。鄰接表就是解決這個問題的一種方法.
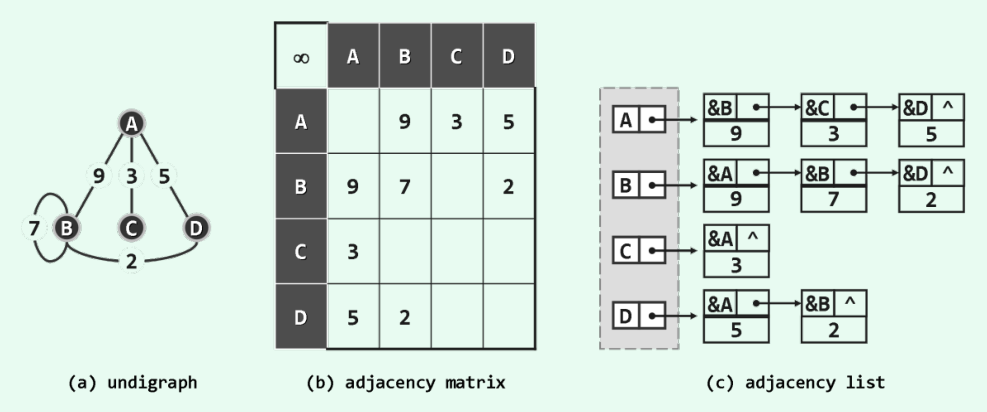
以上圖中的無向圖為例,只需要將b圖依次轉(zhuǎn)化為c圖中的鄰接表。省略掉不存在的邊,可以大大優(yōu)化稀疏表的空間性能。
下附代碼實現(xiàn)
/*鄰接表存儲表示*/typedef struct EdgeNode //邊結(jié)點{int adjvex; //該邊所指向的頂點的位置EdgeNode* next; //指向下一條邊的指針int weight; //和邊相關(guān)的信息,如權(quán)值}edgeNode;typedef struct HeadNode //表頭結(jié)點{char data;EdgeNode* firstarc; //指向第一條依附該頂點的邊的指針}headNode, AdjList[MAXNum]; //AbjList表示一個表頭結(jié)點表typedef struct ALGraph{AdjList vertices;int vexnum, arcnum;}ALGraph;int LocateVex(ALGraph& G, char v)/*找到頂點v的對應下標*/{int i;for (i = 0; i < G.vexnum; i++)if (G.vertices[i].data == v)return i;}void Create(ALGraph& G){int i, j, k, w;char v1, v2;cin >> G.vexnum >> G.arcnum; //輸入總頂點數(shù),總邊數(shù)for (i = 0; i < G.vexnum; i++) //輸入各頂點,構(gòu)造表頭結(jié)點表{cin >> G.vertices[i].data; //輸入頂點值G.vertices[i].firstarc = NULL; //初始化每個表頭結(jié)點的指針域為NULL}for (k = 0; k < G.arcnum; k++) //輸入各邊,構(gòu)造鄰接表{cin >> v1 >> v2 >> w; //輸入一條邊依附的兩個頂點i = LocateVex(G, v1); //找到頂點i的下標j = LocateVex(G, v2); //找到頂點j的下標EdgeNode* p1 = new EdgeNode; //創(chuàng)建一個邊結(jié)點*p1p1->adjvex = j; //其鄰接點域為jp1->next = G.vertices[i].firstarc;p1->weight = w;G.vertices[i].firstarc = p1; // 將新結(jié)點*p插入到頂點v1的邊表頭部/*若為無向圖*//* EdgeNode* p2 = new EdgeNode; //生成另一個對稱的新的表結(jié)點*p2p2->adjvex = i;p2->next = G.vertices[j].firstarc;G.vertices[j].firstarc = p2;*/}}
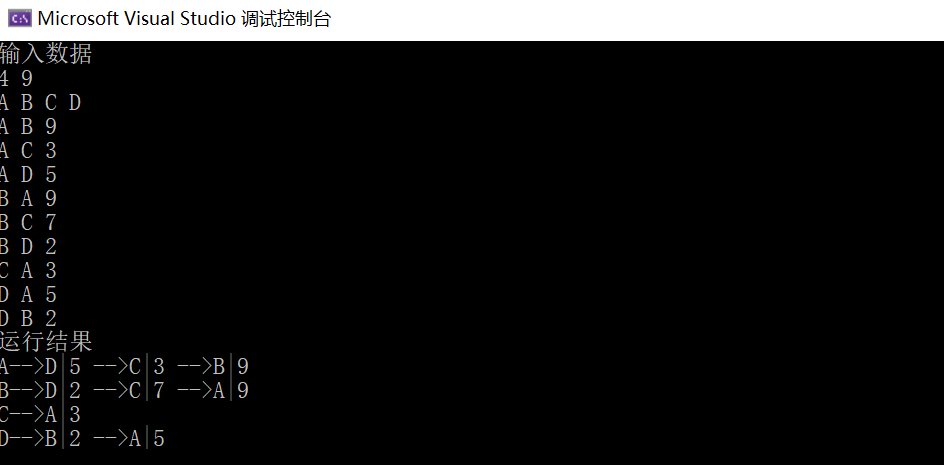
復雜度分析
????????可見,鄰接表所含列表數(shù)等于頂點總數(shù)n,每條邊在其中僅存放一次(有向圖)或兩次(無向圖),故空間總量為O(n + e),與圖自身的規(guī)模相當,較之鄰接矩陣有很大改進。
????????當然,空間性能的這一改進,需以某些方面時間性能的降低為代價。例如查詢兩點之間是否存在邊時共需O(n)時間。
同時,在頂點的處理上,插入頂點的時間復雜度變?yōu)榱薕(1),美中不足的是,其刪除頂點的時間復雜度還是O(n)。
與鄰接矩陣相比,鄰接表在單個邊的處理上略顯乏力,但是它在批量處理上有著強大的優(yōu)勢,因此總體上我們還是偏向于鄰接表。
圖的遍歷
廣度優(yōu)先搜索(BFS)
圖的各種搜索之間所得的遍歷樹不同的決定性因素在于搜索中每一步之后將按照何種策略來選取下一步,這就是BFS和DFS的差別所在。接下來就來了解一下。
廣度優(yōu)先搜索
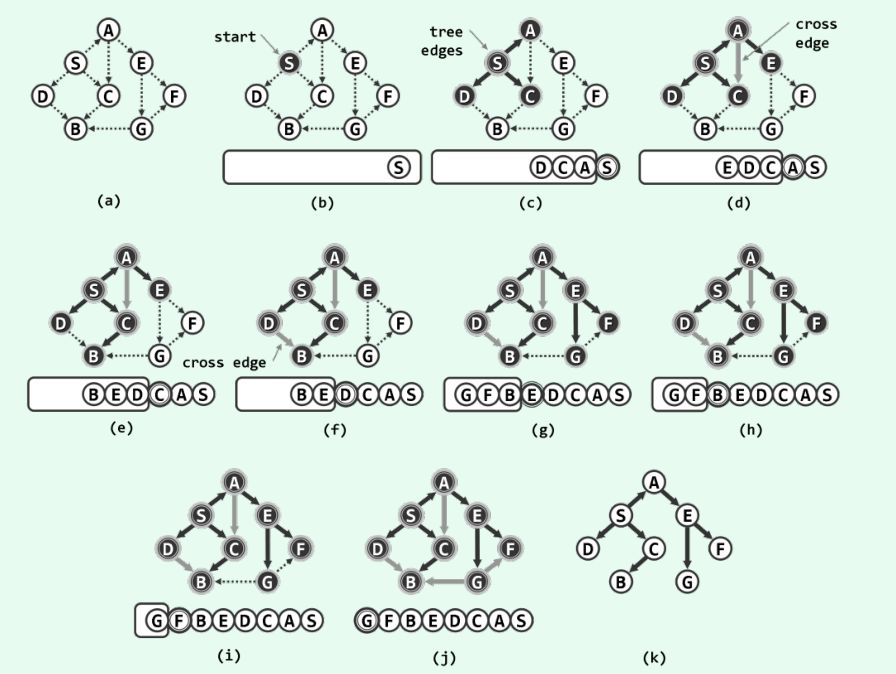
在遍歷的過程中,我們相當于圖轉(zhuǎn)化為一個樹,每個節(jié)點假設都有一個固定的深度,BFS的操作就是每次遍歷的時候都先將同一深度的節(jié)點遍歷完后再進行下一層的遍歷。而下一層的節(jié)點我們預先是不知道的,是需要由上一層節(jié)點的邊來確定,那么我們就需要一個隊列將上一層節(jié)點保存下來,此時隊列中的節(jié)點的深度為k,將深度為k的節(jié)點擴展后的節(jié)點深度為k+1,將這些點中之前未被訪問過的插入到隊列后方,保證了先將k層的遍歷完后,再進行k+1層的遍歷。同時也要將已經(jīng)進行擴展的節(jié)點移除隊列,避免重復訪問。
由于每一次迭代都有一個節(jié)點被訪問,因此至多迭代n次,另一方面,因為不會遺漏每個剛被訪問頂點的任何鄰居,故對于無向圖必能覆蓋s所屬的連通分量(connected component),對于有向圖必能覆蓋以s為起點的可達分量(reachable component)。倘若還有來自其它連通分量或可達分量的頂點,則不妨從該頂點出發(fā),重復上述過程。
????????時間方面,首先需花費O(n + e)時間復位所有頂點和邊的狀態(tài)。不計對子函數(shù)BFS()的調(diào)用,bfs()本身對所有頂點的枚舉共需O(n)時間。而在對BFS()的所有調(diào)用中,每個頂點、每條邊均只耗費O(1)時間,累計O(n + e)。綜合起來,BFS搜索總體僅需O(n + e)時間。
????????下圖是以S為起始節(jié)點開始的BFS示例
下為代碼實現(xiàn)
/*采用鄰接表表示圖的廣度優(yōu)先遍歷*/void?BFS(ALGraph?&G,?char?v0){int u,w,v;??EdgeNode?*p;??cin>>?v0;????????????????????????????????????????????//打印頂點v0v = LocateVex(G, v0); ????????????????????????????????????????????????//找到v0對應的下標visited[v] = 1; ????????????????????????????????????????//頂點v0已被訪問q.push(v0); ????????????????????????????????//將頂點v0入隊while (!q.empty()){u = q.front(); ????????????????????????????????????????//將頂點元素u出隊,開始訪問u的所有鄰接點v = LocateVex(G, u);????????????????????????????????????????????//得到頂點u的對應下標q.pop(); //將頂點u出隊for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍歷頂點u的鄰接點{w = p->adjvex;if (!visited[w]) //頂點p未被訪問{printf("%c ", G.vertices[w].data); ????????//打印頂點pvisited[w] = 1; ????????//頂點p已被訪問q.push(G.vertices[w].data); //將頂點p入隊}}}}
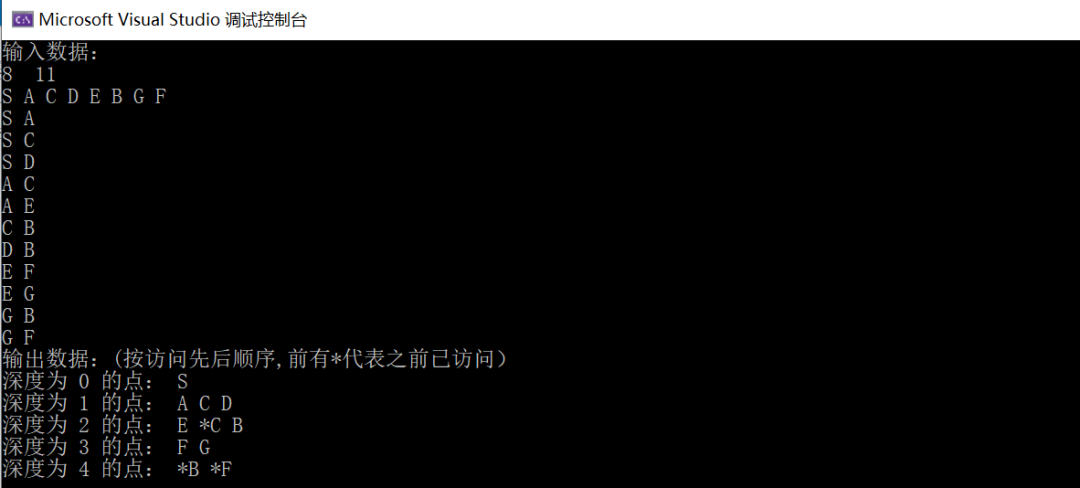
圖的搜索
深度優(yōu)先搜索(DFS)
與BFS不同,DFS是一條路走到黑的(原諒本小編太菜了,說不明白)由遞歸完成。
???每一次遞歸,都先將當前節(jié)點v標記為DISCOVERED(已發(fā)現(xiàn))狀態(tài),再逐一核對其各鄰居u的狀態(tài)并做相應處理。待其所有鄰居均已處理完畢之后,將頂點v置為VISITED(訪問完畢)狀態(tài),便可回溯。
????????若節(jié)點u為UNDISCOVERED(未發(fā)現(xiàn))狀態(tài),則將邊(v, u)為遍歷樹上的一條邊。若節(jié)點u為DISCOVERED(發(fā)現(xiàn))狀態(tài)。
????????若頂點u處于DISCOVERED狀態(tài),則意味著在此處發(fā)現(xiàn)一個有向環(huán)路。此時,在DFS遍歷樹中u必為v的祖先。對于有向圖,頂點u還可能處于VISITED狀態(tài)。此時,只要比對v與u的活躍期,即可判定在DFS樹中v是否為u的祖先。
????????這里為每個頂點v都記錄了被發(fā)現(xiàn)的和訪問完成的時刻。至于為什么要用兩個記錄,這是為了判斷在有向圖中是否為強連通量的問題,這里我們先不解釋,大家有興趣可以查閱一下資料。
????????在回溯返回后,所有的VISITED的點可以確定了父子關(guān)系,形成了一棵遍歷樹。這就是我們需要的DFS樹,與BFS搜索一樣,此時若還有其它的連通或可達分量,則可以其中任何頂點為基點,再次啟動DFS搜索。
????????接下來就是時間分析了。每次迭代中對所有頂點的枚舉共需O(n)時間。每個頂點、每條邊只在子函數(shù)DFS()的某一遞歸實例中耗費O(1)時間,故累計亦不過O(n + e)時間。(忽略了函數(shù)的調(diào)用用的時間)綜合而言,深度優(yōu)先搜索算法也可在O(n + e)時間內(nèi)完成。
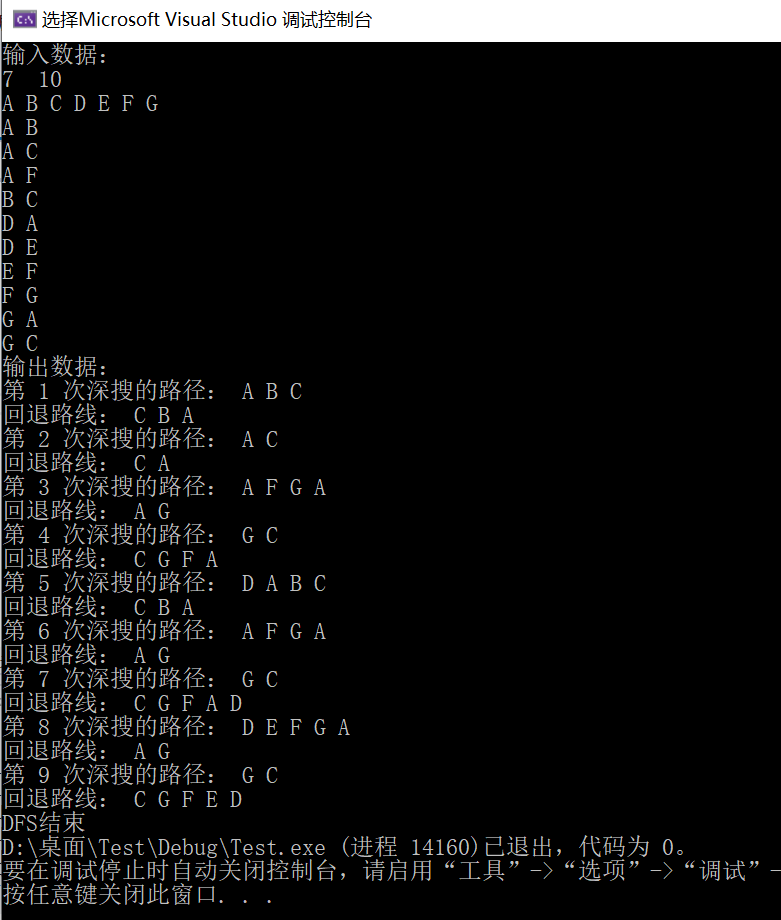
????????下為一個7點,10邊的有向圖進行DFS的詳細過程,大家可以研究下。
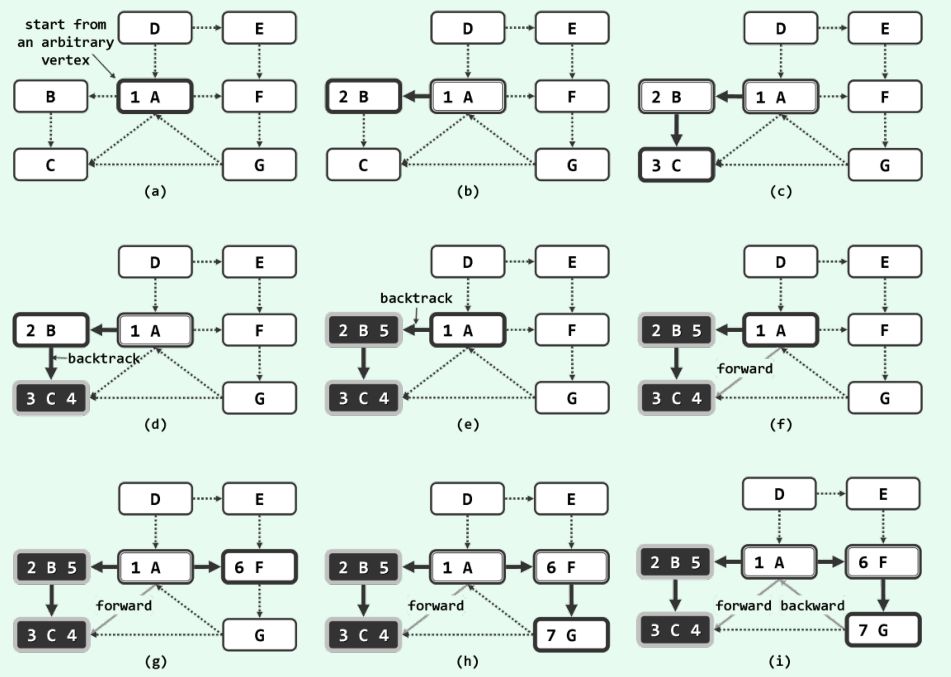
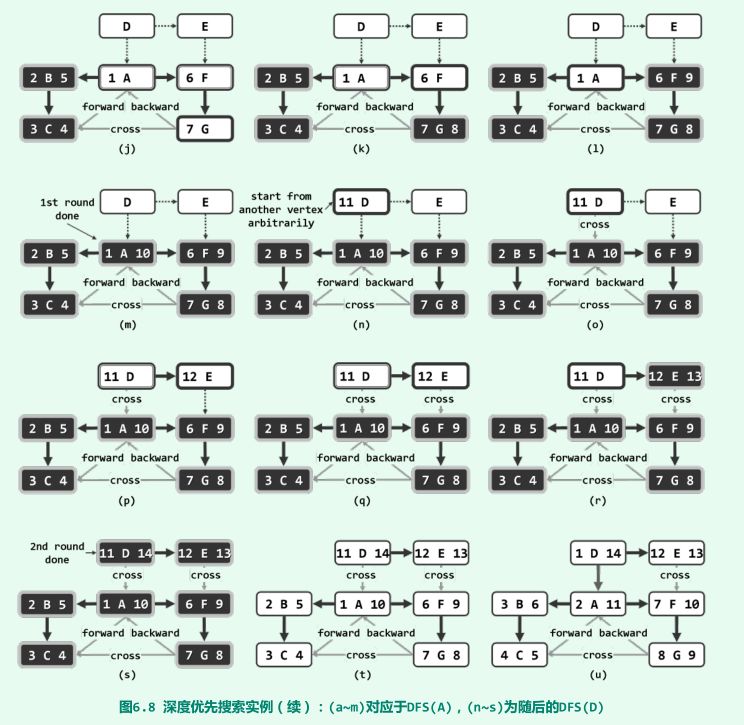
(粗邊框白色,為當前頂點;細邊框白色、雙邊框白色和黑色,分別為處于UNDISCOVERED、DISCOVERED和VISITED狀態(tài)的頂點,左上角的數(shù)字為被發(fā)現(xiàn)時的序號,右上角的數(shù)字為訪問完成時的數(shù)據(jù))
下為代碼實現(xiàn)
void?DFS(ALGraph?&G,?int?v){int w;??cin>>G.vertices[v].data;visited[v] = 1;??EdgeNode?*p?=?new?EdgeNode;p = G.vertices[v].firstarc;while (p){w = p->adjvex;if (!visited[w]) DFS_AL(G, w);p = p->nextarc;}}