線性代數(shù)的本質(zhì)及其在AI中的應(yīng)用

數(shù)學(xué)算法俱樂(lè)部

日期 ： 2021年05月29日       

正文共 ：3910字

來(lái)源 ： 機(jī)器之心

線性代數(shù)是 AI 專(zhuān)家必須掌握的知識(shí)，這已不再是個(gè)秘密。如果不掌握應(yīng)用數(shù)學(xué)這個(gè)領(lǐng)域，你永遠(yuǎn)就只能是「門(mén)外漢」。當(dāng)然，學(xué)習(xí)線性代數(shù)道阻且長(zhǎng)。數(shù)學(xué)，尤其是線性代數(shù)常與枯燥、復(fù)雜和毫無(wú)意義的事物聯(lián)系起來(lái)。不過(guò)你還可以另辟蹊徑。

閱讀完本文后，你將了解到：

• 線性代數(shù)的本質(zhì)；
• 線性代數(shù)的真實(shí)應(yīng)用場(chǎng)景；
• 線性代數(shù)可用于 AI、ML 和數(shù)據(jù)科學(xué)的原因；
• 學(xué)習(xí)線性代數(shù)最有效的方法。

給初學(xué)者的解釋?zhuān)壕€性代數(shù)的本質(zhì)

第一次接觸線性代數(shù)的人，通常會(huì)覺(jué)得線性代數(shù)長(zhǎng)這樣：

看起來(lái)就讓人頭大？你的腦海隨即會(huì)浮現(xiàn)出兩個(gè)問(wèn)題：它們都是從哪兒來(lái)的？為什么需要這些運(yùn)算？

讓我們做個(gè)簡(jiǎn)單的練習(xí)。

線性代數(shù)是計(jì)算數(shù)學(xué)的「主力軍」。我舉個(gè)簡(jiǎn)單的例子來(lái)說(shuō)明。

假設(shè)我們有一根兩端固定的極細(xì)金屬棒，其溫度恒等于零。我們開(kāi)始使用分布式熱源對(duì)棒進(jìn)行加熱，該熱源在點(diǎn) x 的附近，每單位長(zhǎng)度每秒產(chǎn)生 q (x) 焦耳熱量。溫度 t = t (x) 公式該怎么建立？先粗略建模：熱量平衡后，設(shè)點(diǎn) x 的分段為 [x-h, x + h]，來(lái)自熱源的熱流入應(yīng)等于分段兩端的熱通量之和。如果 h 足夠小，那么熱通量可以看作常量（包含 h），該等式可以寫(xiě)成如下形式：

其中 Q_x-h 是通過(guò)左邊界的熱通量，Q_x + h 是通過(guò)右邊界的熱通量。根據(jù)傅立葉定律，熱通量與溫度差成正比（畢竟，你剛跳進(jìn)水里時(shí)感覺(jué)最冷）。因此：

令 h = 1 /N。假設(shè) xi = i · h，其中 i =0, 1, 2, …, N，它們被稱(chēng)為網(wǎng)格。變量 ti = t (xi) 將滿(mǎn)足方程式：

基于邊界條件且 qi = q (xi)，得到線性方程組：

具體來(lái)說(shuō)，這個(gè)系統(tǒng)可以通過(guò)掃描法「正面」解決，但是在實(shí)際模型中，系統(tǒng)變得更加復(fù)雜。線性代數(shù)正好發(fā)揮了作用：

用 A · y = b 的簡(jiǎn)短形式描述系統(tǒng)（這是矩陣乘法的由來(lái)！）；

了解是否有解決方案，以及解決方案是否唯一；

（在本例中）使用簡(jiǎn)單公式 y = A-1 b 來(lái)建模，將 A 看做一個(gè)數(shù)字；

（引入計(jì)算數(shù)學(xué)）建立用于求解線性方程組的有效數(shù)值方法。

這只是從數(shù)學(xué)建模的角度看線性代數(shù)，還有量子力學(xué)、統(tǒng)計(jì)學(xué)等多個(gè)角度。

再以著名問(wèn)題為例，即某網(wǎng)站（或整個(gè)互聯(lián)網(wǎng)）的「網(wǎng)頁(yè)引用排名」問(wèn)題。

假設(shè)有 N 個(gè)頁(yè)面，每頁(yè)可能包含到其他頁(yè)面的鏈接。我們的任務(wù)是確定哪些頁(yè)面最重要。如何準(zhǔn)確地衡量「重要性」是任務(wù)的一部分。我們將以非負(fù)數(shù)（權(quán)重）來(lái)定量表示。先假設(shè)：此頁(yè)面的鏈接越多，其權(quán)重就越大。這種方法有個(gè)缺點(diǎn)：我們沒(méi)有考慮鏈接頁(yè)面的權(quán)重。一個(gè)鏈接權(quán)重越大，其意義也越大，這是合乎邏輯的。考慮到這些因素，我們選擇以下模型：

其中 a_ij 是第 i 頁(yè)到第 j 頁(yè)的鏈接數(shù)，除以第 j 頁(yè)的鏈接總數(shù)。該公式可以理解為：第 i 頁(yè)的權(quán)重等于第 j 頁(yè)的權(quán)重與從第 j 頁(yè)到第 i 頁(yè)的鏈接之比的乘積之和。因此，我們將問(wèn)題簡(jiǎn)化為線性方程組。此外，權(quán)重向量 p 是矩陣 A 的特征向量，對(duì)應(yīng)特征值為 1：p = Ap

Frobenius-Perron 定理保證了該向量的存在（嚴(yán)格來(lái)說(shuō)，矩陣 A 略有修改），通過(guò)簡(jiǎn)單的迭代即可找到。

因此，線性代數(shù)是一套非常通用的思想和工具，可以應(yīng)用于各個(gè)領(lǐng)域。但是「天下沒(méi)有免費(fèi)的午餐」，通用性的代價(jià)是：某些定義和定理有著毫無(wú)必要的復(fù)雜度。不過(guò)事實(shí)并非如此：實(shí)際上，許多抽象目的是簡(jiǎn)化而非復(fù)雜化。「如果它看起來(lái)像鴨子，像鴨子一樣游泳，像鴨子一樣嘎嘎叫，那么它可能就是鴨子」這實(shí)際上就是一種抽象，如果你習(xí)慣了這種抽象概念，將會(huì)非常方便。線性代數(shù)也是一樣。為了更具體地說(shuō)明這一點(diǎn)，讓我們簡(jiǎn)短討論下內(nèi)部來(lái)補(bǔ)充一下「外部檢查」。

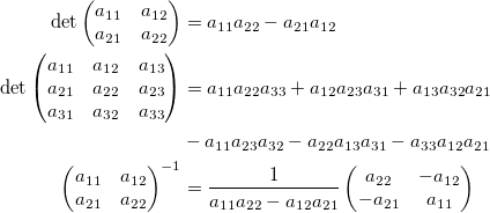
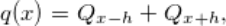
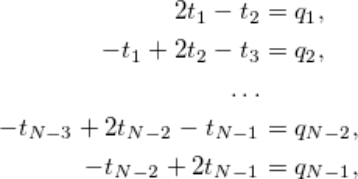
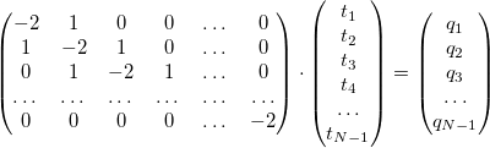
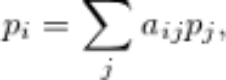
一些你需要知道的線性代數(shù)理論

線性代數(shù)研究的是向量空間以及將一個(gè)向量空間映射到另一個(gè)向量空間的函數(shù)。我們主要考慮線性函數(shù)（對(duì)于任何常數(shù)α和β以及向量 x 和 y，滿(mǎn)足關(guān)系 f (α · x + β · y) = α · f (x) + β · f (y)。也有非線性的函數(shù)（例如二次方程），不過(guò)首先你需要知道什么是向量（以及向量空間），這不像看上去那么簡(jiǎn)單。

教材和課程中通常只是給出一個(gè)抽象的定義，這一定義又常常由 8 點(diǎn)構(gòu)成。有時(shí)一個(gè)矢量空間被視作一個(gè)使用加號(hào)的阿貝爾群，該阿貝爾群滿(mǎn)足四大群公理，并定義了標(biāo)量乘法。但是對(duì)于剛開(kāi)始研究線性代數(shù)的人來(lái)說(shuō)，理解這些著實(shí)困難，學(xué)習(xí)一些具體示例并進(jìn)行類(lèi)比要容易得多。8 條的定義僅僅是這種類(lèi)比的形式。所以我們舉個(gè)例子吧：

向量，是我們每個(gè)人都熟悉的有向線段，多個(gè)有向線段可以組成一個(gè)向量空間。回憶一下多項(xiàng)式，它們可以進(jìn)行通項(xiàng)相加以及系數(shù)相乘。請(qǐng)注意：從代數(shù)的角度來(lái)看，這些多項(xiàng)式的加法運(yùn)算以及多項(xiàng)式與系數(shù)的乘法運(yùn)算，與有向線段運(yùn)算規(guī)則是完全一致的。例如，等式 x + y = y + x（加法交換性）對(duì)有向線段和多項(xiàng)式均成立。因此，多項(xiàng)式的集合是向量空間，而多項(xiàng)式就是向量。

既然多項(xiàng)式類(lèi)似于有向線段，那么它們也肯定有坐標(biāo)。但是如何獲知多項(xiàng)式的坐標(biāo)以及多項(xiàng)式有多少個(gè)坐標(biāo)呢？眾所周知，每個(gè)向量在平面上都有兩個(gè)坐標(biāo)，在空間中則是三個(gè)。為什么會(huì)這樣呢？維度又是什么？線性代數(shù)給出了一個(gè)答案：維度就是線性無(wú)關(guān)向量的最大數(shù)量。線性無(wú)關(guān)是什么意思？如果存在數(shù)字α1, α2, …, αn，其中至少一個(gè)非零，則向量 x1, x2, …, xn 被稱(chēng)為線性相關(guān)。

如果向量不線性相關(guān)，則稱(chēng)它們?yōu)榫€性獨(dú)立。（線性相關(guān)性的概念概括了平行向量和共面向量的概念：兩個(gè)向量在當(dāng)且僅當(dāng)它們平行時(shí)才線性相關(guān)。三個(gè)向量在當(dāng)且僅當(dāng)它們共面時(shí)才線性相關(guān)。）

空間的維數(shù)可以是有限的（維數(shù)不大于 N 的多項(xiàng)式空間），也可以是無(wú)限的（所有多項(xiàng)式空間）。這兩種情況在實(shí)際中都會(huì)出現(xiàn)，但現(xiàn)在我們限制其為有限維的。令向量 x1, x2, …, xn 線性無(wú)關(guān)，n 為空間維數(shù)。任何其他向量 x 都可以唯一地寫(xiě)為 x1, x2, …, xn 的線性組合，相應(yīng)的線性組合的系數(shù)稱(chēng)為坐標(biāo)。

現(xiàn)在，我們對(duì)坐標(biāo)有了嚴(yán)格的定義，但重點(diǎn)不只是這個(gè)：在此過(guò)程中，我們遇到了更基本（更易忽略）的線性組合和線性相關(guān)性的概念。而且我們還了解到，在 n 維線性空間中，最多只能有 n 個(gè)線性無(wú)關(guān)向量。這是線性代數(shù)的基礎(chǔ)之一。

我們知道的仍只是「冰山一角」。但是現(xiàn)在我們可以解決那些顯然與線性代數(shù)無(wú)關(guān)的問(wèn)題了。例如：給定多項(xiàng)式 p 和 q；是否在兩個(gè)變量 R = R (x, y) 中存在多項(xiàng)式，使得對(duì)于所有 t 都有 R (p (t), q (t)) = 0？

「示例」基本結(jié)束了，但仍然有必要講講研究線性代數(shù)的各種方法。我簡(jiǎn)短回顧一下自己的經(jīng)歷，提出幾點(diǎn)建議。

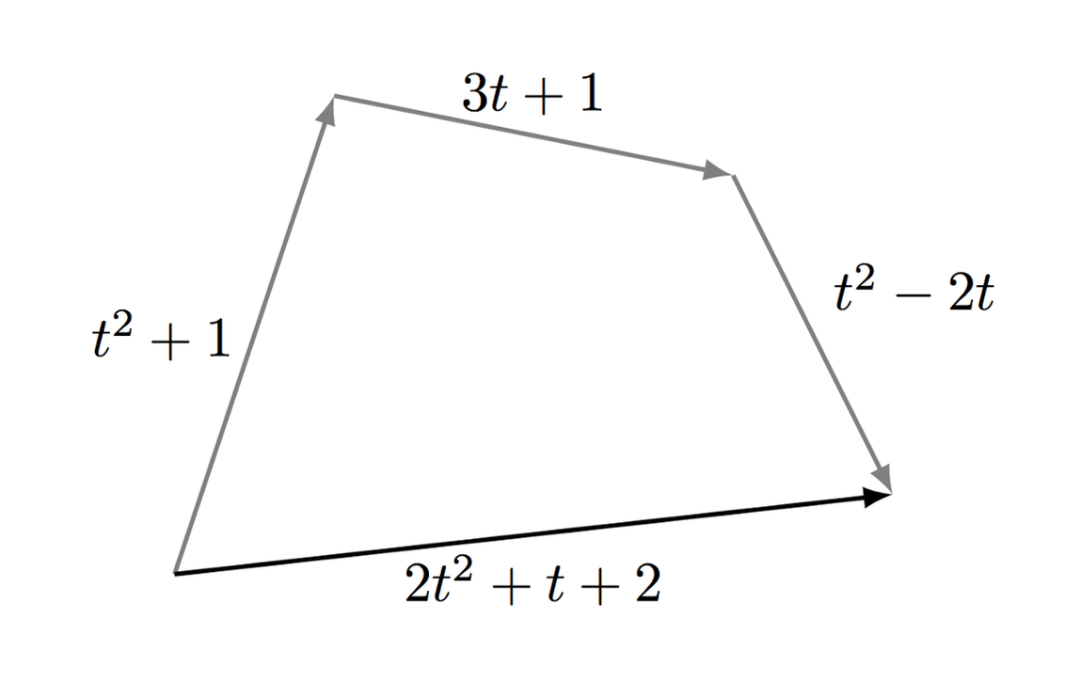
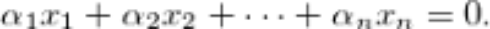
最重要的問(wèn)題：AI 真的需要線性代數(shù)嗎？

這取決于你的目的。如果你只想把人工智能和機(jī)器學(xué)習(xí)的工具當(dāng)作一個(gè)黑匣子，那么你只需要足夠的數(shù)學(xué)計(jì)算就可以確定你的問(wèn)題是否符合模型使用。

如果你想提出新想法，線性代數(shù)則是你必須要學(xué)習(xí)的東西。并不是說(shuō)你需要學(xué)習(xí)有關(guān)數(shù)學(xué)的所有知識(shí)，這樣會(huì)耽擱于此，失去研究其他更重要的東西（如微積分/統(tǒng)計(jì)）的動(dòng)力。

你的目標(biāo)應(yīng)該是使用線性代數(shù)來(lái)找到點(diǎn)與點(diǎn)之間的最短路徑。以下是你所需要掌握的知識(shí)列表：

標(biāo)量、向量、張量：求模（大小）、向量夾角（點(diǎn)積或內(nèi)積）、一個(gè)向量在另一向量上的投影以及依據(jù)自定義的軸向量對(duì)向量的描述和表示

矩陣：矩陣可以將向量的描述從一組基（一組坐標(biāo)軸）轉(zhuǎn)換為另一組基。例如，找出如何將映射應(yīng)用到圖像上并處理圖像。

矩陣中的長(zhǎng)度平方采樣、奇異值分解、低秩逼近是數(shù)據(jù)處理中廣泛采用的幾種方法。

SVD 通常用于主成分分析（PCA）中，而主成分分析又被廣泛用于特征提取以及了解特征或?qū)傩灾g的關(guān)系對(duì)于結(jié)果的重要性上。

線性代數(shù)在機(jī)器學(xué)習(xí)中的應(yīng)用實(shí)例

以下是線性代數(shù)的一些具體示例：

數(shù)據(jù)集和數(shù)據(jù)文件

例如在機(jī)器學(xué)習(xí)中，將模型擬合到一組由數(shù)字組成的類(lèi)似表格的數(shù)據(jù)集上，其中每一行代表一個(gè)觀測(cè)結(jié)果，每一列代表該觀測(cè)值的特征。你發(fā)現(xiàn)相似之處了么？這些數(shù)據(jù)實(shí)際上是一個(gè)矩陣：是線性代數(shù)中的一種關(guān)鍵的數(shù)據(jù)結(jié)構(gòu)。

圖像和照片

你處理的每個(gè)圖像本身就是一個(gè)表結(jié)構(gòu)，對(duì)于黑白圖像，每個(gè)單元格中有一個(gè)寬度和高度以及一個(gè)像素值，而彩色圖像每個(gè)單元格中有三個(gè)像素值。照片是線性代數(shù)矩陣的另一個(gè)例子。

獨(dú)熱編碼

獨(dú)熱編碼是分類(lèi)變量中的一種很流行的編碼。獨(dú)熱編碼是創(chuàng)建表來(lái)表示變量，其中每一列表示一個(gè)類(lèi)別，每一行表示數(shù)據(jù)集中的一個(gè)樣本。

線性回歸

線性回歸是統(tǒng)計(jì)學(xué)中描述變量之間關(guān)系的一種舊方法。在機(jī)器學(xué)習(xí)中，它通常用于預(yù)測(cè)簡(jiǎn)單回歸問(wèn)題中的數(shù)值。

深度學(xué)習(xí)

線性代數(shù)是描述深度學(xué)習(xí)方法的核心，通過(guò)矩陣表示法來(lái)實(shí)現(xiàn)深度學(xué)習(xí)方法，例如谷歌的 TensorFlow Python 庫(kù)，其名稱(chēng)中就有「tensor」一詞。

結(jié)論

下面是我在學(xué)習(xí)這些并不簡(jiǎn)單的數(shù)學(xué)內(nèi)容時(shí)總結(jié)的技巧：

• 在解決有趣的問(wèn)題時(shí)，是最容易理解線性代數(shù)思想和方法的，趣味問(wèn)題有助于理解抽象概念；
• 記得要與其他人（朋友，或論壇）一起學(xué)習(xí)；
• 如果你喜歡按日程表學(xué)習(xí)，請(qǐng)使用在線課程和其他方法。但在將矩陣轉(zhuǎn)換為 Wolfram Alpha 之前，你應(yīng)該學(xué)會(huì)「手撕矩陣」；
• 注意多讀書(shū)，這可以促使你深度思考。

線性代數(shù)的基本概念和定理并非從零開(kāi)始。努力理解本質(zhì)、內(nèi)部邏輯對(duì)拓寬你在這個(gè)主題上的視角很有用。克萊默（Cramer）、高斯（Gauss）、皮亞諾（Peano）等等許多人肯定從中發(fā)現(xiàn)了樂(lè)趣（他們首先取悅了自己），所以學(xué)習(xí)線性代數(shù)的人怎么會(huì)感到無(wú)聊呢？

— THE END —

?14歲考入北大少年班，如今節(jié)衣縮食上課穿膠鞋，卻慷慨資助貧困生

?細(xì)數(shù)二十世紀(jì)最偉大的10大算法

?10部關(guān)于數(shù)學(xué)的頂級(jí)紀(jì)錄片

?假如地球變成甜甜圈形狀，世界會(huì)變成什么樣子？

?應(yīng)用數(shù)學(xué)的強(qiáng)大威力

?丘成桐：本科教育怪事多