位操作運(yùn)算有什么奇技淫巧?(附源碼)
位運(yùn)算
百度百科如下:
程序中的所有數(shù)在計(jì)算機(jī)內(nèi)存中都是以二進(jìn)制的形式儲(chǔ)存的。位運(yùn)算就是直接對(duì)整數(shù)在內(nèi)存中的二進(jìn)制位進(jìn)行操作
位操作的優(yōu)勢(shì)
- 位運(yùn)算是一種底層的運(yùn)算,往往比我們普通的運(yùn)算要快上許多許多
- 位運(yùn)算是最高效而且占用內(nèi)存最少的算法操作,執(zhí)行效率非常高
- 位運(yùn)算操作的是二進(jìn)制數(shù),會(huì)擁有一些二進(jìn)制的特性,在實(shí)際問(wèn)題可以方便運(yùn)用
- 位運(yùn)算只需較低的空間需求
- 位運(yùn)算使用能使程序變得更加簡(jiǎn)潔和優(yōu)美
- 位運(yùn)算可以表示一些狀態(tài)集合
運(yùn)算符號(hào)
下面的a和b都是整數(shù)類(lèi)型,則:
| 含義 | C語(yǔ)言 |
|---|---|
| 按位與 | a & b |
| 按位或 | a | b |
| 按位異或 | a ^ b |
| 按位取反 | ~a |
| 左移 | a << b |
| 帶符號(hào)右移 | a >> b |
| 無(wú)符號(hào)右移 |
優(yōu)先級(jí)
C語(yǔ)言中位運(yùn)算符之間,按優(yōu)先級(jí)順序排列為
| 優(yōu)先級(jí) | 符號(hào) |
|---|---|
| 1 | ~ |
| 2 | <<、>> |
| 3 | & |
| 4 | ^ |
| 5 | | |
| 6 | &=、^=、|=、<<=、>>= |
概念簡(jiǎn)介以及技巧
本文會(huì)以C語(yǔ)言的交互環(huán)境來(lái)做代碼演示
常見(jiàn)的二進(jìn)制位的變換操作
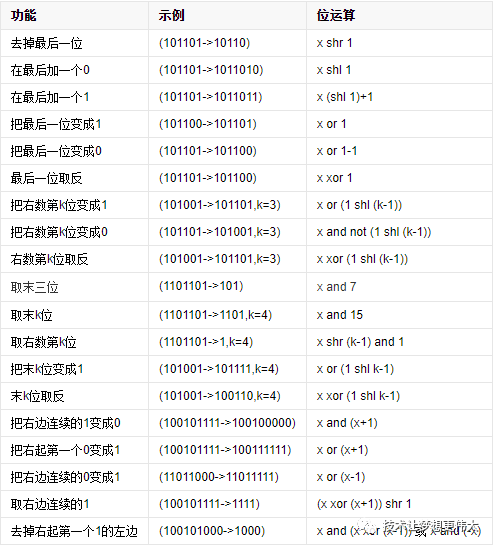
and運(yùn)算 &
- 判斷奇偶數(shù)
對(duì)于除0以外的任意數(shù)x,使用x&1==1作為邏輯判斷即可
if (x&1==1)
{
}
- 判斷某個(gè)二進(jìn)制位是否為1
比如第7位, 0x40轉(zhuǎn)到二進(jìn)制是0100 0000,代表第7位是1.
if (n&0x40)
{
//TODO:添加你要處理的代碼
}
- 字節(jié)讀取
(x >> 0) & 0x000000ff /* 獲取第0個(gè)字節(jié) */
(x >> 8) & 0x000000ff /* 獲取第1個(gè)字節(jié) */
(x >> 16) & 0x000000ff /* 獲取第2個(gè)字節(jié) */
(x >> 24) & 0x000000ff /* 獲取第3個(gè)字節(jié) */
- 判斷一個(gè)數(shù)是不是 22 的指數(shù)
bool isPowerOfTwo(int n) {
if (n <= 0) return false;
return (n & (n - 1)) == 0;
}
- 取余
//得到余數(shù)
int Yu(int num,int n)
{
int i = 1 << n;
return num&(i-1);
}
- 指定二進(jìn)制位數(shù)截取
比如說(shuō)16位二進(jìn)制數(shù)A:1001 1001 1001 1000,如果來(lái)你想獲A的哪一位的值,就把數(shù)字B:0000 0000 0000 0000的那一位設(shè)置為1.
比如說(shuō)我想獲得A的第三位就把B的第三位數(shù)字設(shè)置為1,則B為0000 0000 0000 0100,設(shè)置完之后再把A、B求與, 其結(jié)果若為0,說(shuō)明A的第三位為0,其結(jié)果為1,說(shuō)明A的第三位為1.
同理:若要獲得A的第五位,就把B設(shè)置為0000 0000 0001 0000,之后再求與。
通常在我們的程序中,數(shù)字B被稱(chēng)為掩碼,其含義是專(zhuān)門(mén)用來(lái)測(cè)試某一位是否為0的數(shù)值。
- 統(tǒng)計(jì)二進(jìn)制中 1 的個(gè)數(shù)
利用x=x&(x-1),會(huì)將x用二進(jìn)制表示時(shí)最右邊的一個(gè)1變?yōu)?,因?yàn)閤-1會(huì)將該位變?yōu)?.
int Count(int x)
{ int sum=0;
while(x)
{ sum++;
x=x&(x-1);
}
return sum;
}
or操作
- 生成組合編碼,進(jìn)行狀態(tài)壓縮
當(dāng)把二進(jìn)制當(dāng)作集合使用時(shí),可以用or操作來(lái)增加元素。合并編碼 在對(duì)字節(jié)碼進(jìn)行加密時(shí),加密后的兩段bit需要重新合并成一個(gè)字節(jié),這時(shí)就需要使用or操作。
- 求一個(gè)數(shù)的二進(jìn)制表達(dá)中0的個(gè)數(shù)
int Grial(int x)
{
int count = 0;
while (x + 1)
{
count++;
x |= (x + 1);
}
return count;
}
xor操作
- 兩個(gè)整數(shù)交換變量名
void swap(int &a, int &b) {
a ^= b;
b ^= a;
a ^= b;
}
- 判斷兩個(gè)數(shù)是否異號(hào)
int x = -1, y = 2;
bool f = ((x ^ y) < 0); // true
int x = 3, y = 2;
bool f = ((x ^ y) < 0); // false
- 數(shù)據(jù)加密
將需要加密的內(nèi)容看做A,密鑰看做B,A ^ B=加密后的內(nèi)容C。而解密時(shí)只需要將C ^ 密鑰B=原內(nèi)容A。如果沒(méi)有密鑰,就不能解密!
#include
#include
#include
#define KEY 0x86
int main()
{
char p_data[16] = {"Hello World!"};
char Encrypt[16]={0},Decode[16]={0};
int i;
for(i = 0; i < strlen(p_data); i++)
{
Encrypt[i] = p_data[i] ^ KEY;
}
for(i = 0; i < strlen(Encrypt); i++)
{
Decode[i] = Encrypt[i] ^ KEY;
}
printf("Initial date: %s\n",p_data);
printf("Encrypt date: %s\n",Encrypt);
printf("Decode date: %s\n",Decode);
return 0;
}
- 數(shù)字判重
利用了二進(jìn)制數(shù)的性質(zhì):x^y^y = x。我們可見(jiàn),當(dāng)同一個(gè)數(shù)累計(jì)進(jìn)行兩次xor操作,相當(dāng)于自行抵銷(xiāo)了,剩下的就是不重復(fù)的數(shù)
- 找出沒(méi)有重復(fù)的數(shù)
int find(int[] arr){
int tmp = arr[0];
for(int i = 1;i < arr.length; i++){
tmp = tmp ^ arr[i];
}
return tmp;
}
not操作
- 交換符號(hào)
int reversal(int a) {
return ~a + 1;
}
- 取絕對(duì)值(效率高)
- n>>31 取得n的符號(hào)
- 若n為正數(shù),n>>31等于0
- 若n為負(fù)數(shù),n>>31等于-1
- 若n為正數(shù) n^0=0,數(shù)不變
- 若n為負(fù)數(shù),有n^-1 需要計(jì)算n和-1的補(bǔ)碼,然后進(jìn)行異或運(yùn)算,結(jié)果n變符號(hào)并且為n的絕對(duì)值減1,再減去-1就是絕對(duì)值
int abs(int n)
{
return (n ^ (n >> 31)) - (n >> 31);
}
也可以這樣使用
int abs(int n)
{
int i = n >> 31;
return i == 0 ? n : (~n + 1);
}
- 從低位到高位.將n的第m位置1
將1左移m-1位找到第m位,得到000...1...000, n在和這個(gè)數(shù)做或運(yùn)算
int setBitToOne(int n, int m)
{
return n | (1 << (m-1));
}
同理從低位到高位,將n的第m位置0,代碼如下
int setBitToZero(int n, int m)
{
return n & ~(1 << (m-1));
}
shl操作 & shr操作
- 求2的N次方
1<- 高低位交換
unsigned short a = 34520;
a = (a >> 8) | (a << 8);
- 進(jìn)行二進(jìn)制逆序
unsigned short a = 34520;
a = ((a & 0xAAAA) >> 1) | ((a & 0x5555) << 1);
a = ((a & 0xCCCC) >> 2) | ((a & 0x3333) << 2);
a = ((a & 0xF0F0) >> 4) | ((a & 0x0F0F) << 4);
a = ((a & 0xFF00) >> 8) | ((a & 0x00FF) << 8);
- 獲得int型最大最小值
int getMaxInt()
{
return (1 << 31) - 1;//2147483647, 由于優(yōu)先級(jí)關(guān)系,括號(hào)不可省略
}
int getMinInt()
{
return 1 << 31;//-2147483648
}
- m的n次方
//自己重寫(xiě)的pow()方法
int pow(int m , int n){
int sum = 1;
while(n != 0){
if(n & 1 == 1){
sum *= m;
}
m *= m;
n = n >> 1;
}
return sum;
}
- 找出不大于N的最大的2的冪指數(shù)
int findN(int n){
n |= n >> 1;
n |= n >> 2;
n |= n >> 4;
n |= n >> 8 // 整型一般是 32 位,上面我是假設(shè) 8 位。
return (n + 1) >> 1;
}
- 二分查找32位整數(shù)的前導(dǎo)0個(gè)數(shù)
int nlz(unsigned x)
{
int n;
if (x == 0) return(32);
n = 1;
if ((x >> 16) == 0) {n = n +16; x = x <<16;}
if ((x >> 24) == 0) {n = n + 8; x = x << 8;}
if ((x >> 28) == 0) {n = n + 4; x = x << 4;}
if ((x >> 30) == 0) {n = n + 2; x = x << 2;}
n = n - (x >> 31);
return n;
}
- 位圖的操作
將 x 的第 n 位置1,可以通過(guò) x |= (x << n) 來(lái)實(shí)現(xiàn)
set_bit(char x, int n);
將 x 的第 n 位清0,可以通過(guò) x &= ~(1 << n) 來(lái)實(shí)現(xiàn)
clr_bit(char x, int n);
取出 x 的第 n 位的值,可以通過(guò) (x >> n) & 1 來(lái)實(shí)現(xiàn)
get_bit(char x, int n);
如下:
#define clr_bit(x, n) ( (x) &= ~(1 << (n)) )
#define set_bit(x, n) ( (x) |= (1 << (n)) )
#define get_bit(x, n) ( ((x)>>(n)) & 1 )
綜合應(yīng)用
以下僅列出,感興趣可以參考下面鏈接.
關(guān)于操作計(jì)數(shù)方法
計(jì)算整數(shù)的符號(hào)
檢測(cè)兩個(gè)整數(shù)是否具有相反的符號(hào)
計(jì)算無(wú)分支的整數(shù)絕對(duì)值(abs)
計(jì)算兩個(gè)整數(shù)的最小值(最小值)或最大值(最大值),而無(wú)需分支
確定整數(shù)是否為2的冪
標(biāo)志延伸
- 從恒定位寬擴(kuò)展的符號(hào)
- 從可變位寬擴(kuò)展的符號(hào)
- 通過(guò)3個(gè)操作從可變位寬擴(kuò)展符號(hào) 有條件地設(shè)置或清除位而不分支
有條件地否定一個(gè)值而不分支
根據(jù)掩碼合并兩個(gè)值中的位
計(jì)數(shù)位設(shè)置
- 計(jì)數(shù)位設(shè)置,幼稚的方式
- 計(jì)算由查找表設(shè)置的位
- 數(shù)位集,Brian Kernighan的方式
- 使用64位指令對(duì)14、24或32位字中設(shè)置的位進(jìn)行計(jì)數(shù)
- 并行設(shè)置計(jì)數(shù)位
- 從最高有效位到給定位置的計(jì)數(shù)位的設(shè)置(等級(jí))
- 從給定的計(jì)數(shù)(等級(jí))中選擇位位置(從最高有效位開(kāi)始)
計(jì)算奇偶校驗(yàn)(如果設(shè)置了奇數(shù)位數(shù),則為1,否則為0)
- 天真地計(jì)算單詞的奇偶性
- 通過(guò)查找表計(jì)算奇偶校驗(yàn)
- 使用64位乘法和模數(shù)除法計(jì)算字節(jié)的奇偶校驗(yàn)
- 用乘法計(jì)算單詞的奇偶校驗(yàn)
- 并行計(jì)算奇偶校驗(yàn)
交換價(jià)值
- 用減法和加法交換值
- 用XOR交換值
- 用XOR交換單個(gè)位
反轉(zhuǎn)位序列
反轉(zhuǎn)位是顯而易見(jiàn)的方式
- 逐字查找表中的位反轉(zhuǎn)
- 通過(guò)3個(gè)操作(64位乘法和模數(shù)除法)反轉(zhuǎn)字節(jié)中的位
- 通過(guò)4個(gè)操作反轉(zhuǎn)字節(jié)中的位(64位乘法,無(wú)除法)
- 通過(guò)7個(gè)操作反轉(zhuǎn)字節(jié)中的位(無(wú)64位,僅32位)
- 與5 * lg(N)個(gè)運(yùn)算并行地反轉(zhuǎn)N位數(shù)量
模數(shù)除法(又名計(jì)算余數(shù))
- 在不進(jìn)行除法運(yùn)算的情況下,將模數(shù)除以1 << s(顯而易見(jiàn))
- 在不進(jìn)行除法運(yùn)算的情況下以(1 << s)-1計(jì)算模數(shù)除法
- 不進(jìn)行除法運(yùn)算就并行計(jì)算(1 << s)-1的模數(shù)除法
查找整數(shù)的整數(shù)對(duì)數(shù)2(又稱(chēng)最高位集的位置)
- 使用O(N)運(yùn)算找到MSB N設(shè)置為整數(shù)的對(duì)數(shù)2(顯而易見(jiàn)的方法)
- 查找具有64位IEEE浮點(diǎn)數(shù)的整數(shù)的整數(shù)對(duì)數(shù)2
- 使用查找表找到整數(shù)的對(duì)數(shù)2
- 在O(lg(N))運(yùn)算中找到N位整數(shù)的對(duì)數(shù)2
- 使用乘法和查找在O(lg(N))操作中找到N位整數(shù)的對(duì)數(shù)2
查找整數(shù)的對(duì)數(shù)以10為底的整數(shù)
查找整數(shù)的整數(shù)對(duì)數(shù)10
查找32位IEEE浮點(diǎn)數(shù)的整數(shù)對(duì)數(shù)基數(shù)2
查找32位IEEE浮點(diǎn)的pow(2,r)根的整數(shù)對(duì)數(shù)基數(shù)2(對(duì)于無(wú)符號(hào)整數(shù)r)
計(jì)算連續(xù)的尾隨零位(或查找位索引)
- 線性計(jì)算右邊的連續(xù)零位(后綴)
- 并行計(jì)算右側(cè)連續(xù)的零位(后綴)
- 通過(guò)二進(jìn)制搜索計(jì)算右邊連續(xù)的零位(跟蹤)
- 通過(guò)強(qiáng)制轉(zhuǎn)換為浮點(diǎn)數(shù)來(lái)計(jì)算右側(cè)連續(xù)的零位(跟蹤)
- 用模數(shù)除法和查找計(jì)算右邊連續(xù)的零位(跟蹤)
- 用乘法和查找計(jì)數(shù)右邊連續(xù)的零位(后跟)
通過(guò)浮法舍入到2的下一個(gè)最高冪
向上舍入到2的下一個(gè)最高冪
交織位(也稱(chēng)為計(jì)算莫頓數(shù))
- 交錯(cuò)位的明顯方式
- 通過(guò)表查找交織位
- 帶64位乘法的交織位
通過(guò)二進(jìn)制幻數(shù)交錯(cuò)位
測(cè)試單詞中的字節(jié)范圍(并計(jì)算出現(xiàn)的次數(shù))
- 確定單詞是否為零字節(jié)
- 確定一個(gè)單詞的字節(jié)數(shù)是否等于n
- 確定一個(gè)單詞的字節(jié)數(shù)是否小于n
- 確定單詞的字節(jié)數(shù)是否大于n
- 確定單詞是否在m和n之間有一個(gè)字節(jié)
按詞典順序計(jì)算下一位排列
更多內(nèi)容可以查看:
http://graphics.stanford.edu/~seander/bithacks.html
推薦閱讀:給所有入門(mén)編程者的幾點(diǎn)建議!
【編程之美】模塊化編程到底有多重要
關(guān)注微信公眾號(hào)『技術(shù)讓夢(mèng)想更偉大』,后臺(tái)回復(fù)“m”查看更多內(nèi)容,回復(fù)“加群”加入技術(shù)交流群。
長(zhǎng)按前往圖中包含的公眾號(hào)關(guān)注
