BN，Batch Normalization，就是在深度神經(jīng)網(wǎng)絡(luò)訓(xùn)練過程中使得每一層神經(jīng)網(wǎng)絡(luò)的輸入保持相近的分布。

BN訓(xùn)練和測試時的參數(shù)是一樣的嗎？

對于BN，在訓(xùn)練時，是對每一批的訓(xùn)練數(shù)據(jù)進(jìn)行歸一化，也即用每一批數(shù)據(jù)的均值和方差。

而在測試時，比如進(jìn)行一個樣本的預(yù)測，就并沒有batch的概念，因此，這個時候用的均值和方差是全量訓(xùn)練數(shù)據(jù)的均值和方差，這個可以通過移動平均法求得。

對于BN，當(dāng)一個模型訓(xùn)練完成之后，它的所有參數(shù)都確定了，包括均值和方差，gamma和bata。

BN訓(xùn)練時為什么不用全量訓(xùn)練集的均值和方差呢？

因為在訓(xùn)練的第一個完整epoch過程中是無法得到輸入層之外其他層全量訓(xùn)練集的均值和方差，只能在前向傳播過程中獲取已訓(xùn)練batch的均值和方差。那在一個完整epoch之后可以使用全量數(shù)據(jù)集的均值和方差嘛？

對于BN，是對每一批數(shù)據(jù)進(jìn)行歸一化到一個相同的分布，而每一批數(shù)據(jù)的均值和方差會有一定的差別，而不是用固定的值，這個差別實際上也能夠增加模型的魯棒性，也會在一定程度上減少過擬合。

但是一批數(shù)據(jù)和全量數(shù)據(jù)的均值和方差相差太多，又無法較好地代表訓(xùn)練集的分布，因此，BN一般要求將訓(xùn)練集完全打亂，并用一個較大的batch值，去縮小與全量數(shù)據(jù)的差別。

Dropout 是在訓(xùn)練過程中以一定的概率的使神經(jīng)元失活，即輸出為0，以提高模型的泛化能力，減少過擬合。

Dropout 在訓(xùn)練和測試時都需要嗎？

Dropout 在訓(xùn)練時采用，是為了減少神經(jīng)元對部分上層神經(jīng)元的依賴，類似將多個不同網(wǎng)絡(luò)結(jié)構(gòu)的模型集成起來，減少過擬合的風(fēng)險。

而在測試時，應(yīng)該用整個訓(xùn)練好的模型，因此不需要dropout。

Dropout 如何平衡訓(xùn)練和測試時的差異呢？

Dropout ，在訓(xùn)練時以一定的概率使神經(jīng)元失活，實際上就是讓對應(yīng)神經(jīng)元的輸出為0

假設(shè)失活概率為 p ，就是這一層中的每個神經(jīng)元都有p的概率失活，如下圖的三層網(wǎng)絡(luò)結(jié)構(gòu)中，如果失活概率為0.5，則平均每一次訓(xùn)練有3個神經(jīng)元失活，所以輸出層每個神經(jīng)元只有3個輸入，而實際測試時是不會有dropout的，輸出層每個神經(jīng)元都有6個輸入，這樣在訓(xùn)練和測試時，輸出層每個神經(jīng)元的輸入和的期望會有量級上的差異。

因此在訓(xùn)練時還要對第二層的輸出數(shù)據(jù)除以（1-p）之后再傳給輸出層神經(jīng)元，作為神經(jīng)元失活的補(bǔ)償，以使得在訓(xùn)練時和測試時每一層輸入有大致相同的期望。

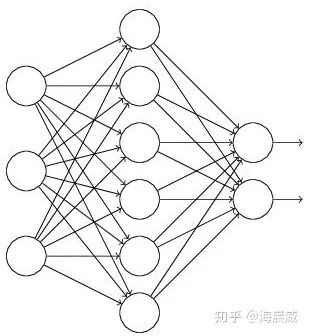
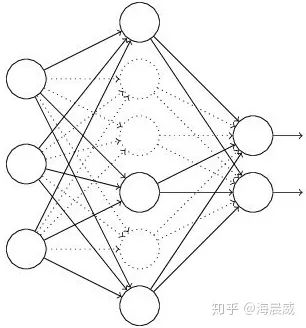
dropout部分參考：

https://blog.csdn.net/program_developer/article/details/80737724

BN和Dropout共同使用時會出現(xiàn)的問題

BN和Dropout單獨使用都能減少過擬合并加速訓(xùn)練速度，但如果一起使用的話并不會產(chǎn)生1+1>2的效果，相反可能會得到比單獨使用更差的效果。

相關(guān)的研究參考論文：

Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift

https://arxiv.org/abs/1801.05134

本論文作者發(fā)現(xiàn)理解 Dropout 與 BN 之間沖突的關(guān)鍵是網(wǎng)絡(luò)狀態(tài)切換過程中存在神經(jīng)方差的（neural variance）不一致行為。試想若有圖一中的神經(jīng)響應(yīng) X，當(dāng)網(wǎng)絡(luò)從訓(xùn)練轉(zhuǎn)為測試時，Dropout 可以通過其隨機(jī)失活保留率（即 p）來縮放響應(yīng)，并在學(xué)習(xí)中改變神經(jīng)元的方差，而 BN 仍然維持 X 的統(tǒng)計滑動方差。這種方差不匹配可能導(dǎo)致數(shù)值不穩(wěn)定（見下圖中的紅色曲線）。而隨著網(wǎng)絡(luò)越來越深，最終預(yù)測的數(shù)值偏差可能會累計，從而降低系統(tǒng)的性能。簡單起見，作者們將這一現(xiàn)象命名為「方差偏移」。事實上，如果沒有 Dropout，那么實際前饋中的神經(jīng)元方差將與 BN 所累計的滑動方差非常接近（見下圖中的藍(lán)色曲線），這也保證了其較高的測試準(zhǔn)確率。

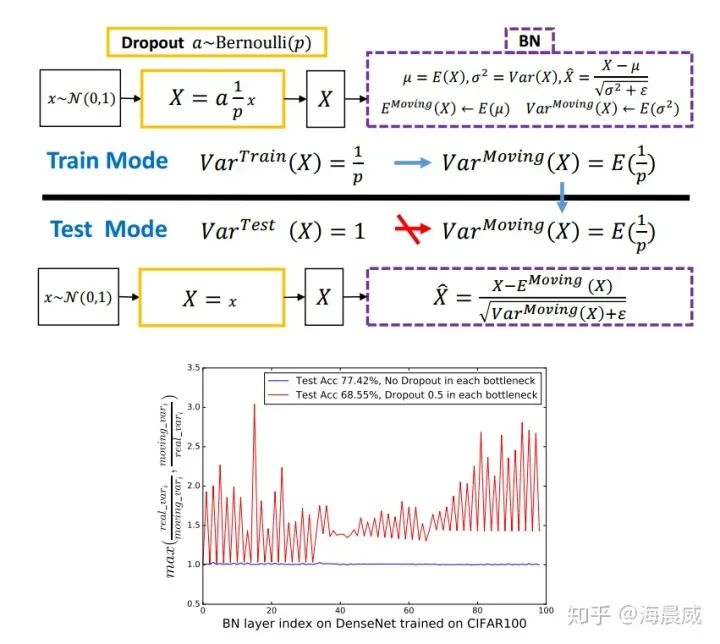
作者采用了兩種策略來探索如何打破這種局限。一個是在所有 BN 層后使用 Dropout，另一個就是修改 Dropout 的公式讓它對方差并不那么敏感，就是高斯Dropout。

第一個方案比較簡單，把Dropout放在所有BN層的后面就可以了，這樣就不會產(chǎn)生方差偏移的問題，但實則有逃避問題的感覺。

第二個方案來自Dropout原文里提到的一種高斯Dropout，是對Dropout形式的一種拓展。作者進(jìn)一步拓展了高斯Dropout，提出了一個均勻分布Dropout，這樣做帶來了一個好處就是這個形式的Dropout（又稱為“Uout”）對方差的偏移的敏感度降低了，總得來說就是整體方差偏地沒有那么厲害了。

該部分參考：

https://www.jiqizhixin.com/articles/2018-01-23-4

https://zhuanlan.zhihu.com/p/33101420