C語言函數(shù)遞歸


前言
上章節(jié)講到C語言的函數(shù),詳細內(nèi)容請參見上章節(jié)。本章節(jié)主要是給大家介紹下C語言函數(shù)中的難點函數(shù)遞歸。

遞歸概念
在C語言中,函數(shù)調(diào)用可以從main()函數(shù),其他函數(shù)或同一函數(shù)本身進行。遞歸函數(shù)定義如下:一個函數(shù)調(diào)用函數(shù)自身稱為遞歸函數(shù)。應該非常小心地使用遞歸函數(shù),因為當一個函數(shù)自己調(diào)用它進入無限循環(huán)時。當函數(shù)進入無限循環(huán)時,函數(shù)執(zhí)行永遠不會完成。我們應該定義退出函數(shù)調(diào)用的條件,以便遞歸函數(shù)終止。當一個函數(shù)被自己調(diào)用時,第一個調(diào)用仍在執(zhí)行中,直到調(diào)用最后一個調(diào)用。每次調(diào)用函數(shù)調(diào)用時,該函數(shù)都會將執(zhí)行控件返回到上一個函數(shù)調(diào)用。舉個


從階乘看遞歸
階乘是基斯頓·卡曼(Christian Kramp,1760~1826)于 1808 年發(fā)明的運算符號,是數(shù)學術(shù)語。一個正整數(shù)的階乘(factorial)是所有小于及等于該數(shù)的正整數(shù)的積,并且0的階乘為1。自然數(shù)n的階乘寫作n!。1808年,基斯頓·卡曼引進這個表示法。亦即n!=1×2×3×...×n。階乘亦可以遞歸方式定義:0!=1,n!=(n-1)!×n。
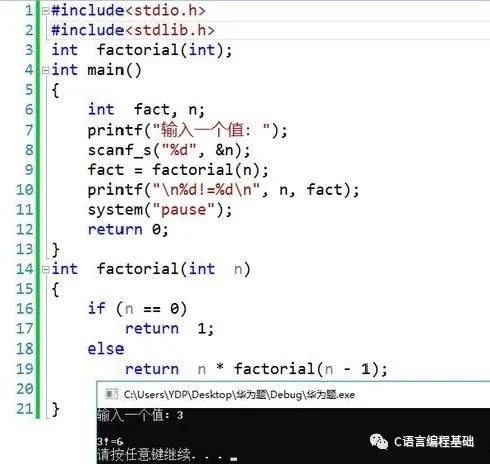
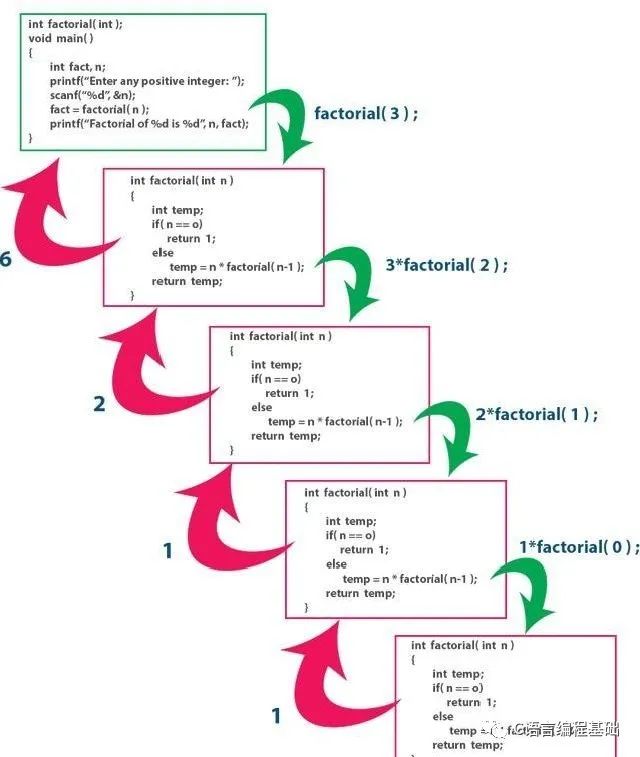
在上面的示例程序中,factorial()函數(shù)調(diào)用是從main()函數(shù)啟動的,其值為3.在factorial()函數(shù)內(nèi),函數(shù)調(diào)用factorial(2),factorial(1)和factorial(0)被調(diào)用遞歸。在該程序執(zhí)行過程中,函數(shù)調(diào)用factorial(3)仍在執(zhí)行中,直到函數(shù)調(diào)用factorial(2),factorial(1)和factorial(0)的執(zhí)行完成。類似地,函數(shù)調(diào)用factorial(2)仍在執(zhí)行中,直到函數(shù)調(diào)用factorial(1)和factorial(0)的執(zhí)行完成。以相同的方式,函數(shù)調(diào)用factorial(1)保持執(zhí)行,直到函數(shù)調(diào)用factorial(0)的執(zhí)行完成。上述程序的完整執(zhí)行過程如下圖所示:
遞歸函數(shù)的優(yōu)點是定義簡單,邏輯清晰。理論上,所有的遞歸函數(shù)都可以寫成循環(huán)的方式,但循環(huán)的邏輯不如遞歸清晰。使用遞歸函數(shù)需要注意防止棧溢出。在計算機中,函數(shù)調(diào)用是通過棧(stack)這種數(shù)據(jù)結(jié)構(gòu)實現(xiàn)的,每當進入一個函數(shù)調(diào)用,棧就會加一層棧幀,每當函數(shù)返回,棧就會減一層棧幀。由于棧的大小不是無限的,所以,遞歸調(diào)用的次數(shù)過多,會導致棧溢出。可以試試factorial(1000)。
解決遞歸調(diào)用棧溢出的方法是通過尾遞歸優(yōu)化,事實上尾遞歸和循環(huán)的效果是一樣的,所以,把循環(huán)看成是一種特殊的尾遞歸函數(shù)也是可以的。尾遞歸是指,在函數(shù)返回的時候,調(diào)用自身本身,并且,return語句不能包含表達式。這樣,編譯器或者解釋器就可以把尾遞歸做優(yōu)化,使遞歸本身無論調(diào)用多少次,都只占用一個棧幀,不會出現(xiàn)棧溢出的情況。
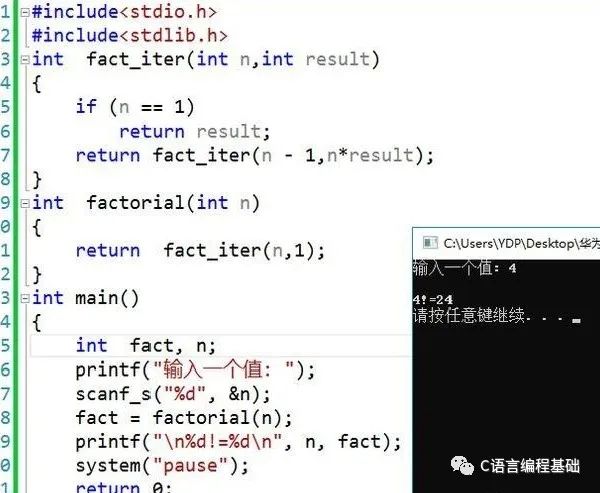
可以看到,return fact_iter(n- 1, n* result)僅返回遞歸函數(shù)本身,n- 1和n* result在函數(shù)調(diào)用前就會被計算,不影響函數(shù)調(diào)用。尾遞歸調(diào)用時,如果做了優(yōu)化,棧不會增長,因此,無論多少次調(diào)用也不會導致棧溢出。

尾言
使用遞歸函數(shù)的優(yōu)點是邏輯簡單清晰,缺點是過深的調(diào)用會導致棧溢出。針對尾遞歸優(yōu)化的語言可以通過尾遞歸防止棧溢出。尾遞歸事實上和循環(huán)是等價的,沒有循環(huán)語句的編程語言只能通過尾遞歸實現(xiàn)循環(huán)。標準的解釋器沒有針對尾遞歸做優(yōu)化,任何遞歸函數(shù)都存在棧溢出的問題。
作業(yè):
漢諾塔的移動可以用遞歸函數(shù)非常簡單地實現(xiàn)。

請編寫move(n, a, b, c)函數(shù),它接收參數(shù)n,表示3個柱子A、B、C中第1個柱子A的盤子數(shù)量,然后打印出把所有盤子從A借助B移動到C的方法。
駿馬是跑出來的,強兵是打出來的。駕馭命運的舵是奮斗。不抱有一絲幻想,不放棄一點機會,不停止一日前進腳步。

