構(gòu)建距離矩陣求最短距離
題目
最近刷題的時(shí)候發(fā)現(xiàn)了這么一個場景,在一個?N * M?的二維矩陣上有5個點(diǎn),并指定其起始點(diǎn)和終止點(diǎn),求途徑剩余三個點(diǎn)的最短路徑。
具體描述見下圖,S?是起始點(diǎn),E?為終止點(diǎn),其余三點(diǎn)為?A,B,C。當(dāng)然原題還有很多限制,比如滿足什么條件的能通過啊,什么什么條件的不能通過啊等等,此處簡單化對待。
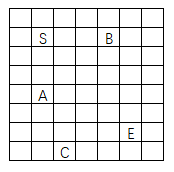
分析
可能的路徑分析
通過觀察可知,此題可以走的路徑有6種,分別為:
??S - A - B - C - E
??S - B - A - C - E
??S - A - C - B - E
??S - C - A - B - E
??S - B - C - A - E
??S - C - B - A - E
其實(shí),這個就是我們上一篇的集合元素的排列與組合中講的方法。
當(dāng)然,此處點(diǎn)的數(shù)量是固定的,我們可以簡單的直接寫出來路徑。當(dāng)然有可以用上篇文章中的代碼模板求出來所有可能的路徑。
兩點(diǎn)間的最短距離
二維矩陣中的兩點(diǎn)之間的最短距離通常可以用?BFS?算法求解,具體可以參照?BFS DFS 解題模板?的模板來實(shí)現(xiàn),這里不再多講。
多個點(diǎn)路徑的最短距離
經(jīng)分析可知,每條路徑上相鄰的兩點(diǎn)的距離是最短的話,那這條路線上所有的兩個相鄰點(diǎn)的最短路徑之和則就是這條路徑的最短距離了。那么怎么優(yōu)雅地獲取每兩個點(diǎn)之間的最短路徑呢?
假設(shè)我們有這么一個矩陣,如下:
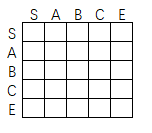
改矩陣就是我們本章節(jié)要提到的距離矩陣,每個元素表示對應(yīng)的行和列的最短路徑,假如已經(jīng)計(jì)算完畢,那么可能長下面這個樣子:
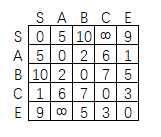
上面的矩陣中填的值只是個樣子,無窮大表示兩點(diǎn)之間不可達(dá)。那么怎么計(jì)算這些值就看我們的算法了。
算法實(shí)現(xiàn)
以下代碼僅展示了核心算法邏輯,請不要糾結(jié)變量未初始化等問題
import?java.util.*;
/**
?*?通過計(jì)算距離矩陣求最短路徑的模板
?*
?*?以下代碼認(rèn)為可移動的地圖是一個二維矩陣(原理適用于所有類似問題,但部分代碼需要根據(jù)實(shí)際修改)
?*?移動規(guī)則為可以上下左右移動(不能超出二維矩陣)
?*/
public?class?DistanceArray?{
????//?@formatter:off
????//?路徑上的所有點(diǎn),每個先的坐標(biāo)由兩個元素組成,分別表示二維數(shù)組的兩個下標(biāo)
????//?例如:POINTS?=?new?int[][]{{0,?0},?{2,?5}};
????static?int[][]?POINTS?=?new?int[][]{{},?{},?{},?{},?{}};
????//?距離矩陣,矩陣上的任意值的下標(biāo)對應(yīng)POINTS上對應(yīng)的點(diǎn),值表示兩點(diǎn)間最短距離????
????static?int[][]?DISTANCES?=?new?int[POINTS.length][POINTS.length];
????//?矩陣的長度和寬度
????static?int?N,?M;
????//?矩陣中的點(diǎn)向上下左右四個方向移動的偏移量
????static?int[][]?MOVE?=?new?int[][]{
????????????{0,?1},?{0,?-1},?{1,?0},?{-1,?0}
????};
????//?假設(shè)二維矩陣上有5個點(diǎn),從0到4有6種路徑
????static?int[][]?ROUTE?=?new?int[][]{
????????????{0,?1,?2,?3,?4},
????????????{0,?2,?1,?3,?4},
????????????{0,?1,?3,?2,?4},
????????????{0,?3,?1,?2,?4},
????????????{0,?2,?3,?1,?4},
????????????{0,?3,?2,?1,?4}
????};
????
????static?Queue<int[]>?QUEUE?=?new?ArrayDeque<>();
????static?List<int[]>?NEXT_ITEMS?=?new?ArrayList<>();
????static?boolean[][]?VISITED;
????
????static?int?MIN;?//?最短路徑
????//?@formatter:on
????public?static?void?main(String[]?args)?{
????????//?初始化距離矩陣
????????initDistanceArray();
????????//?找最小距離
????????findMin();
????????//?打印結(jié)果
????????System.out.printf("min?distance?is?%d",?MIN);
????}
????/**
?????*?找最小值
?????*/
????private?static?void?findMin()?{
????????MIN?=?Integer.MAX_VALUE;
????????//?遍歷所有路徑
????????for?(int[]?route?:?ROUTE)?{
????????????int?distance?=?0;
????????????boolean?arrived?=?true;
????????????//?遍歷當(dāng)前路徑上的每一個點(diǎn),并累計(jì)距離
????????????for?(int?i?=?1;?i?<?route.length;?i++)?{
????????????????int?subMin?=?DISTANCES[route[i]][route[i?-?1]];
????????????????if?(subMin?==?Integer.MIN_VALUE)?{
????????????????????arrived?=?false;
????????????????????break;?//?不可達(dá)
????????????????}?else?{
????????????????????distance?+=?subMin;
????????????????}
????????????}
????????????if?(arrived)?{
????????????????//?抵達(dá)重點(diǎn),求最小值
????????????????MIN?=?Math.min(MIN,?distance);
????????????}
????????}
????????if?(MIN?==?Integer.MAX_VALUE)?{
????????????MIN?=?-1;?//?所有路徑不可達(dá)
????????}
????}
????/**
?????*?初始化距離矩陣
?????*/
????private?static?void?initDistanceArray()?{
????????for?(int?start?=?0;?start?<?POINTS.length;?start++)?{
????????????//?end的起始值從start?+?1取,則不用考慮去重(實(shí)際就是組合算法)
????????????int[]?stepDis?=?minDistance(POINTS[start],?start?+?1);
????????????for?(int?end?=?start?+?1;?end?<?POINTS.length;?end++)?{
????????????????//?A到B的距離等于B到A的距離,所以設(shè)置兩個值
????????????????DISTANCES[start][end]?=?stepDis[end];
????????????????DISTANCES[end][start]?=?stepDis[end];
????????????}
????????}
????}
????/**
?????*?計(jì)算指定點(diǎn)到后續(xù)點(diǎn)的最短距離
?????*?@param?start?指定的起始點(diǎn)
?????*?@param?idx?下一個點(diǎn)的的POINTS的下標(biāo)
?????*?@return?指定點(diǎn)到后續(xù)點(diǎn)的最短距離。idx之前的距離無效
?????*/
????private?static?int[]?minDistance(int[]?start,?int?idx)?{
????????QUEUE.clear();
????????NEXT_ITEMS.clear();
????????VISITED?=?new?boolean[N][M];
????????//?當(dāng)前點(diǎn)的后續(xù)點(diǎn)個數(shù),即待計(jì)算距離的個數(shù)
????????int?calcCount?=?POINTS.length?-?idx;
????????int[]?resp?=?new?int[POINTS.length];
????????Arrays.fill(resp,?Integer.MIN_VALUE);
????????QUEUE.offer(start);
????????VISITED[start[0]][start[1]]?=?true;
????????int?step?=?0;
????????while?(!QUEUE.isEmpty())?{
????????????while?(!QUEUE.isEmpty())?{
????????????????int[]?curr?=?QUEUE.poll();
????????????????//?判斷當(dāng)前的點(diǎn)是否到達(dá)了某個后續(xù)點(diǎn)
????????????????for?(int?end?=?idx;?end?<?POINTS.length;?end++)?{
????????????????????if?(curr[0]?==?POINTS[end][0]?&&?curr[1]?==?POINTS[end][1])?{
????????????????????????resp[end]?=?step;?//?設(shè)置距離
????????????????????????calcCount--;?//?待計(jì)算量減一
????????????????????}
????????????????}
????????????????if?(calcCount?==?0)?{
????????????????????return?resp;?//?全部計(jì)算完畢,返回
????????????????}
????????????????for?(int[]?shift?:?MOVE)?{
????????????????????int?nx?=?curr[0]?+?shift[0];
????????????????????int?ny?=?curr[1]?+?shift[1];
????????????????????if?(nx?>=?0?&&?nx?<?N?&&?ny?>=?0?&&?ny?<?M)?{
????????????????????????//?移動后的點(diǎn)在二維矩陣內(nèi)
????????????????????????if?(!VISITED[nx][ny])?{
????????????????????????????//?偏移后的點(diǎn)沒有被訪問過
????????????????????????????VISITED[nx][ny]?=?true;
????????????????????????????NEXT_ITEMS.add(new?int[]{nx,?ny});
????????????????????????}
????????????????????}
????????????????}
????????????}
????????????step++;
????????????QUEUE.addAll(NEXT_ITEMS);
????????????NEXT_ITEMS.clear();
????????}
????????return?resp;
????}
}最后
??以上的代碼算法除了在二維矩陣中可以使用外,在圖的結(jié)構(gòu)中也能使用
??以上代碼可能還有進(jìn)一步優(yōu)化(時(shí)間或空間)的地方,歡迎多多交流
??我感覺上面的代碼實(shí)現(xiàn)是否可改為?迪杰斯特拉?算法,待驗(yàn)證
原文:https://www.jeremysong.cn/cn/distance-array/
歡迎關(guān)注我的公眾號“須彌零一”,更多技術(shù)文章第一時(shí)間推送。
