【收藏】萬字解析Scipy的使用技巧!
物理常量
常用單位
special函數(shù)庫
非線性方程組求解
最小二乘擬合
計算函數(shù)局域最小值
計算全域最小值
解線性方程組
最小二乘解
特征值和特征向量
連續(xù)概率分布
離散概率分布
核密度函數(shù)
二項分布,泊松分布,伽馬分布
二項分布
泊松分布
伽馬分布
學(xué)生分布(t-分布)和t檢驗
卡方分布和卡方檢驗
數(shù)值積分
球的體積
解常微分方程
ode類
常數(shù)和特殊函數(shù)
物理常量
from?scipy?import?constants?as?C
print("光速:",C.c)
print('普朗克常數(shù):',C.h)
光速:299792458.0
普朗克常數(shù):6.62607004e-34
常用單位
print('一英里:',C.mile)
print('一英寸',C.inch)
一英里:1609.3439999999998
一英寸 0.0254
special函數(shù)庫
Scipy中的special模塊是一個非常完整的函數(shù)庫,其中包含了基本數(shù)學(xué)函數(shù),特殊數(shù)學(xué)函數(shù)以及numpy中所出現(xiàn)的所有函數(shù)。伽馬函數(shù)是概率統(tǒng)計學(xué)中經(jīng)常出現(xiàn)的一個特殊函數(shù),它的計算公司如下:
from?scipy?import?special?as?S
print(S.gamma(4))
6.0
擬合與優(yōu)化-optimize
optimize模塊提供了許多數(shù)值優(yōu)化算法,這里主要對其中的非線性方程組求解、數(shù)值擬合和函數(shù)最小值進行介紹
非線性方程組求解
fsolve()可以對非線性方程組進行求解,它的基本調(diào)用形式為fsolve(func,x0),其中func是計算方程組誤差的函數(shù),它的參數(shù)x是一個數(shù)組,其值為方程組的一組可能的解。func返回將x代入方程組之后得到的每個方程的誤差,x0為未知數(shù)的一組初始解
from?math?import?sin,cos
from?scipy?import?optimize
def?f(x):
????x0,x1,x2=x.tolist()
????return?[
????????5*x1+3,
????????4*x0*x0-2*sin(x1*x2),
????????x1*x2-1.5
????]
result=optimize.fsolve(f,[1,-1,1])
print(result)
print(f(result))
[ 0.70622057 -0.6 -2.5 ]
[0.0, -8.881784197001252e-16, 0.0]
在對方程組進行求解時,fsolve()會自動計算方程組在某點對各個未知變量的偏導(dǎo)數(shù),這些偏導(dǎo)數(shù)組成一個二維數(shù)組,數(shù)學(xué)上稱之為雅閣比矩陣。如果方程組中的未知數(shù)很多,而與每個方程有關(guān)聯(lián)的未知數(shù)較少,即雅各比矩陣比較稀疏的時候,將計算雅各比矩陣的函數(shù)最為參數(shù)傳遞給fsolve(),這能大幅度提高運算速度
def?j(x):
????x0,x1,x2=x.tolist()
????return?[
????????[0,5,0],
????????[8*x0,-2*x2*cos(x1*x2),-2*x1*cos(x1*x2)],
????????[0,x2,x1]
????]
result=optimize.fsolve(f,[1,-1,1],fprime=j)
print(result)
print(f(result))
[ 0.70622057 -0.6 -2.5 ]
[0.0, -8.881784197001252e-16, 0.0]
最小二乘擬合
在optimize模塊中,可以使用leastsq()對數(shù)據(jù)進行最小二乘擬合。只需要將計算誤差的函數(shù)和待確定參數(shù)的初始值傳遞給它即可。
import?numpy?as?np
from?scipy?import?optimize
x=?np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
y=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
def?residuals(p):
????k,b=p
????return?y-(k*x+b)
r=optimize.leastsq(residuals,[1,1])
print(r)
????
(array([0.61349535, 1.79409255]), 3)
接下來是一個擬合正弦波函數(shù)的例子
import?matplotlib.pyplot?as?pl?
def?func(x,p):
????a,k,theta=p
????return?a*np.sin(2*np.pi*k*x+theta)
def?residuals(p,y,x):
????return?y-func(x,p)
x=np.linspace(0,2*np.pi,100)
a,k,theta=10,0.34,np.pi/6?#真實參數(shù)
y0=func(x,[a,k,theta])
y1=y0+2*np.random.randn(len(x))#隨機噪聲
p0=[7,0.4,0]#第一次試錯參數(shù)
plsq=optimize.leastsq(residuals,p0,args=(y1,x))
print('真實參數(shù):',a,k,theta)
print('擬合參數(shù):',plsq[0])
pl.plot(x,y1,'o',label=u'帶噪聲的實驗數(shù)據(jù)')
pl.plot(x,y0,'o',label=u'真實數(shù)據(jù)')
pl.plot(x,func(x,plsq[0]),label=u'擬合數(shù)據(jù)')
pl.legend(loc='best')
pl.show()
真實參數(shù):10 0.34 0.5235987755982988
擬合參數(shù):[9.81307133 0.34167968 0.4651311 ]
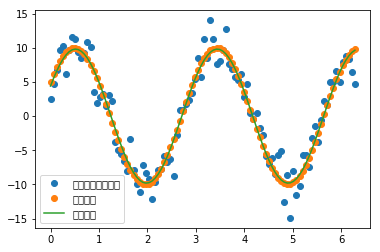
對于這種一維曲線擬合,optimize庫還提供了一個curve_fit()函數(shù),她的目標(biāo)函數(shù)與leastsq稍有不同,各個待優(yōu)化參數(shù)直接作為函數(shù)的參數(shù)傳入
def?func2(x,A,k,theta):
????return?A*np.sin(2*np.pi*k*x+theta)
popt,_=optimize.curve_fit(func2,x,y1,p0=p0)
print(popt)
[9.81307133 0.34167968 0.46513111]
計算函數(shù)局域最小值
optimize庫還提供了許多求函數(shù)最小值的算法:Nelder-Mead,Powell,CG,BFGS,Newton-CG,L-BFGS-B等。下面將使用來實現(xiàn)各個算法
import?numpy?as?np
from?scipy?import?optimize
def?target_func(x,y):
????return?(1-x)**2+(y-x**2)**2
class?Target_function(object):
????def?__init__(self):
????????self.f_points=[]
????????self.fprime_points=[]
????????self.fhess_points=[]
????????
????def?f(self,p):
????????x,y=p.tolist()
????????z=target_func(x,y)
????????self.f_points.append((x,y))
????????return?z
????def?fprime(self,p):
????????x,y=p.tolist()
????????self.fprime_points.append((x,y))
????????dx=-2+2*x-100*x*(y-x**2)
????????dy=200*y-200*x**2
????????return?np.array([dx,dy])
????def?fhess(self,p):
????????x,y=p.tolist()
????????self.fhess_points.append((x,y))
????????return?np.array([[2*(600*x**2-200*y+1),-400*x],[-400*x,200]])
def?fmin_demo(meathod):
????target=Target_function()
????init_point=(1,-1)
????res=optimize.minimize(target.f,init_point,method=meathod,jac=target.fprime,hess=target.fhess)
????return?res,[np.array(points)?for?points?in?(target.f_points,target.fprime_points,target.fhess_points)]
meathods=('Nelder-Mead',"Powell","CG","BFGS","Newton-CG","L-BFGS-B")
for?meathod?in?meathods:
????res,(f_points,fprime_points,fhess_points)=fmin_demo(meathod)
????print(meathod,float(res['fun']),len(f_points),len(fprime_points),len(fhess_points))
Nelder-Mead 3.9257142525324585e-10 88 0 0
Powell 1.3065508742723008e-29 178 0 0
CG 0.34126318409689027 16 4 0
BFGS 0.3618490736691562 59 48 0
Newton-CG 0.8729598762728193 25 14 2
L-BFGS-B 0.007274931919728303 108 108 0
計算全域最小值
前面的幾種算法,只能計算局域的最小值,optimize還提供了幾種能進行全局優(yōu)化的算法,
import?matplotlib.pyplot?as?pl?
def?func(x,p):
????a,k,theta=p
????return?a*np.sin(2*np.pi*k*x+theta)
def?sum_erro(p,y,x):
????return?np.sum((y-func(x,p))**2)
x=np.linspace(0,2*np.pi,100)
a,k,theta=10,0.34,np.pi/6?#真實參數(shù)
y0=func(x,[a,k,theta])
y1=y0+2*np.random.randn(len(x))#隨機噪聲
result=optimize.basinhopping(sum_erro,(1,1,2),niter=30,minimizer_kwargs={'method':'L-BFGS-B',
?????????????????????????????????????????????????????????????????????????'args':(y1,x)})
print(result)
fun: 349.13579066361183
lowest_optimization_result: fun: 349.13579066361183
hess_inv: <3x3 LbfgsInvHessProduct with dtype=float64>
jac: array([-2.27373675e-05, 6.53699317e-03, 2.16004992e-04])
message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
nfev: 212
nit: 31
status: 0
success: True
x: array([ 9.70865421, -0.34042705, 2.60072193])
message: ['requested number of basinhopping iterations completed successfully']
minimization_failures: 0
nfev: 4876
nit: 30
x: array([ 9.70865421, -0.34042705, 2.60072193])
w = min(1.0, np.exp(-(energy_new - energy_old) * self.beta))
線性代數(shù)
numpy和scipy都提供了線性代數(shù)函數(shù)庫linalg,但是SciPy的線性代數(shù)庫比numpy更全面
解線性方程組
numpy.linalg.solve(A,b)和scipy.linalg(A,b)都可以用來解線性方程組Ax=b
from?scipy?import?linalg
m,n=500,50
A=np.random.rand(m,m)
B=np.random.rand(m,n)
X1=np.dot(linalg.inv(A),B)
X2=linalg.solve(A,B)
print(X2)
print(np.allclose(X1,X2))
%timeit?np.dot(linalg.inv(A),B)
%timeit?linalg.solve(A,B)
[[-2.45127873 -0.13882212 1.26994732 ... -0.07598084 0.5579381
0.11674061]
[-0.48192061 -0.50430038 0.44186608 ... -0.03831083 0.32654131
-0.39466819]
[ 2.75605805 -0.18499216 -2.68391499 ... -0.04944263 -1.2672175
1.49844271]
...
[-1.18737097 -0.11455363 1.63027891 ... -0.10635036 1.05193909
-1.18149741]
[-0.57979299 -0.71344473 -0.21270016 ... -0.12685799 -0.16155777
-0.26904821]
[ 3.87852776 0.89917524 -2.85888188 ... 0.49715813 -0.84375228
0.59423434]]
True
16 ms ± 630 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
125 ms ± 2.54 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
最小二乘解
lstsq()比solve()更一般化,他不要求矩陣A是正方形,也就是說方程的個數(shù)可以少于未知數(shù)的個數(shù)。它找到一組解使得||b-Ax||最小。我們稱得到的結(jié)果為最小二乘解,即它使得所有的等式的誤差的平方和最小。
from?numpy.lib.stride_tricks?import?as_strided
def?make_data(m,n,noise_scale):
????np.random.seed(42)
????x=np.random.standard_normal(m)
????h=np.random.standard_normal(n)
????y=np.convolve(x,h)
????yn=y+np.random.standard_normal(len(y))*noise_scale*np.max(y)
????return?x,yn,h
def?solve_h(x,y,n):
????X=as_strided(x,shape=(len(x)-n+1,n),strides=(x.itemsize,x.itemsize))
????Y=y[n-1:len(x)]
????h=linalg.lstsq(X,Y)
????return?print(h[0][::-1])
x,yn,h=make_data(1000,100,0.4)
H1=solve_h(x,yn,120)
print('\n')
H1=solve_h(x,yn,80)
[ 1.02122711 1.12065143 -0.22757846 -1.01482501 1.31553835 0.53934731
1.31544876 0.93354187 1.27032238 -1.04168272 1.39750754 0.22519527
1.65410631 -0.96828011 1.79938629 0.11834929 -1.04443277 -0.68345965
0.04055329 0.7373408 0.26798303 -0.35391692 0.43032291 2.54117049
1.5931832 -0.47924337 -0.09995263 -0.34079478 0.42672859 -0.57032596
-0.5692853 -1.33584647 0.67352005 1.15372941 -0.29870762 1.27445328
-1.31249404 -0.82773274 0.18633994 1.28741445 1.38310911 -0.72534511
1.63964897 0.20082523 -0.47593153 0.58676419 0.85587444 -1.18609796
1.33102096 1.4884538 -0.72843958 0.41312483 0.39393151 -0.30053536
-1.30768415 0.21844389 0.00721972 1.58552414 0.48198959 -1.35023746
0.95909454 -3.71653816 1.37521461 -2.30624762 -0.34215011 -0.66428877
-1.79324755 1.43632782 0.39008346 0.4303981 -0.16790823 0.24939367
0.03675145 -0.94940883 0.67301812 -0.4547047 -1.39794423 -0.81050119
1.4524133 1.04121964 -0.75267186 -0.63258586 -0.45911214 2.11669412
0.40868679 0.53877741 0.80653726 0.71999221 -0.51239799 -0.20112018
-0.71409175 -0.75806901 0.5769544 -0.34864085 0.25527214 0.09671489
-0.04065381 -2.54555059 0.86283462 0.26381314 0.3739484 -0.2581965
0.0916473 -0.39948138 0.46340919 -0.56208375 0.61496994 0.31602602
-0.07288319 0.58254865 0.36038835 -0.3290176 -0.26704998 -0.30263886
0.17307369 -0.16058557 -0.41234224 -0.36123138 -0.57788693 0.30877377]
[ 0.96773811 1.12646313 -0.30935837 -1.00509498 1.2201378 0.67971688
1.02739602 0.89526009 1.37648044 -0.85252762 1.44601678 0.25236444
1.72078754 -0.9927266 1.88968057 0.06650502 -1.00347387 -0.53370158
-0.0379239 0.71894608 0.27874111 -0.66537211 0.33213193 2.55632089
1.49701153 -0.26306165 0.08649175 -0.2826383 0.57646337 -0.71425788
-0.67594548 -1.33111543 0.54923527 1.0362481 -0.08508374 1.10258261
-1.38818785 -0.91201096 0.34062721 1.17273205 1.34629229 -0.60255703
1.74184096 0.13687935 -0.39040247 0.80540905 1.01834963 -1.26912905
1.29109522 1.38615364 -0.82248199 0.25405713 0.5205031 -0.41546992
-1.18200963 -0.01033187 0.05177474 1.54314201 0.32479266 -1.22399043
1.12254575 -3.43895907 1.36536803 -2.41062701 -0.26560136 -0.51458247
-1.8375391 1.30052796 0.49158457 0.36672221 -0.24684166 0.19931159
0.06812972 -0.77958986 0.69666545 -0.47117273 -1.33281541 -0.6192343
1.6301638 0.83173623]
特征值和特征向量
a=np.array([[1,0.3],[0.1,0.9]])
linalg.eig(a)#第一個元組是特征值,第二個是特征向量
(array([1.13027756+0.j, 0.76972244+0.j]), array([[ 0.91724574, -0.79325185],
[ 0.3983218 , 0.60889368]]))
統(tǒng)計—stats
連續(xù)概率分布
連續(xù)隨機變量對象都有如下方法:
rvs: 對隨機變量進行隨機取值,可以通過size參數(shù)指定輸出的數(shù)組大小 pdf: 隨機變量的概率密度函數(shù) cdf: 隨機變量的累積分布函數(shù),她是概率密度函數(shù)的積分 sf: 隨機變量的生存函數(shù),它的值是1-cdf(t) ppf: 累積分布函數(shù)的反函數(shù) stat: 計算隨機變量的期望值和方差 fit: 對一組隨機取樣進行擬合,找出最適合取樣數(shù)據(jù)的概率密度函數(shù)的系數(shù)
以下是隨機概率分布的所有方法:
from?scipy?import?stats
[k?for?k,v?in?stats.__dict__.items()?if?isinstance(v,stats.rv_continuous)]
['ksone',
'kstwobign',
'norm',
'alpha',
'anglit',
'arcsine',
'beta',
'betaprime',
'bradford',
'burr',
'burr12',
'fisk',
'cauchy',
'chi',
'chi2',
'cosine',
'dgamma',
'dweibull',
'expon',
'exponnorm',
'exponweib',
'exponpow',
'fatiguelife',
'foldcauchy',
'f',
'foldnorm',
'frechet_r',
'weibull_min',
'frechet_l',
'weibull_max',
'genlogistic',
'genpareto',
'genexpon',
'genextreme',
'gamma',
'erlang',
'gengamma',
'genhalflogistic',
'gompertz',
'gumbel_r',
'gumbel_l',
'halfcauchy',
'halflogistic',
'halfnorm',
'hypsecant',
'gausshyper',
'invgamma',
'invgauss',
'invweibull',
'johnsonsb',
'johnsonsu',
'laplace',
'levy',
'levy_l',
'levy_stable',
'logistic',
'loggamma',
'loglaplace',
'lognorm',
'gilbrat',
'maxwell',
'mielke',
'kappa4',
'kappa3',
'nakagami',
'ncx2',
'ncf',
't',
'nct',
'pareto',
'lomax',
'pearson3',
'powerlaw',
'powerlognorm',
'powernorm',
'rdist',
'rayleigh',
'reciprocal',
'rice',
'recipinvgauss',
'semicircular',
'skewnorm',
'trapz',
'triang',
'truncexpon',
'truncnorm',
'tukeylambda',
'uniform',
'vonmises',
'vonmises_line',
'wald',
'wrapcauchy',
'gennorm',
'halfgennorm',
'argus']
以下以正態(tài)分布為例,展示相關(guān)函數(shù)
from?scipy?import?stats
x=stats.norm(loc=1,scale=2)#loc參數(shù)指定期望,scale指定標(biāo)準(zhǔn)差
x.stats()
(array(1.), array(4.))
y=x.rvs(size=10000)#對隨機變量取10000個值
np.mean(y),np.var(y)
(1.0312783366175413, 4.022155545295567)
有些隨機分布除了loc和scale參數(shù)之外,還需要額外的形狀參數(shù)。例如伽馬分布可用于描述等待K個獨立隨機事件發(fā)生所需要的時間,k就是伽馬分布的形狀參數(shù)
print(stats.gamma.stats(1))
print(stats.gamma.stats(2.0))
(array(1.), array(1.))
(array(2.), array(2.))
伽馬分布的尺度參數(shù)和隨機事件發(fā)生的頻率有關(guān),由scale參數(shù)指定:
stats.gamma.stats(2.0,scale=2.0)
(array(4.), array(8.))
當(dāng)隨機分布有額外的形狀參數(shù)時,它所對應(yīng)的rvs()和pdf()等方法都會增加額外的參數(shù)來接收形狀參數(shù)。
x=stats.gamma.rvs(2,scale=2,size=4)
stats.gamma.pdf(x,2,scale=2)
array([0.16915721, 0.17582402, 0.17898158, 0.12960963])
X=stats.gamma(2,scale=2)
X.pdf(x)
array([0.16915721, 0.17582402, 0.17898158, 0.12960963])
離散概率分布
以下是離散概率分布的所有方法
[k?for?k,v?in?stats.__dict__.items()?if?isinstance(v,stats.rv_discrete)]
['binom',
'bernoulli',
'nbinom',
'geom',
'hypergeom',
'logser',
'poisson',
'planck',
'boltzmann',
'randint',
'zipf',
'dlaplace',
'skellam']
x=range(1,7)
p=[0.4,0.2,0.1,0.1,0.1,0.1]
dice=stats.rv_discrete(values=(x,p))
dice.rvs(size=20)
array([1, 2, 6, 1, 2, 1, 2, 2, 2, 5, 1, 2, 1, 4, 1, 5, 1, 1, 1, 6])
sample=dice.rvs(size=(20000,50))
sample_mean=np.mean(sample,axis=1)
核密度函數(shù)
_,bins,step=pl.hist(sample_mean,bins=100,normed=True,histtype='step',label=u'直方統(tǒng)計圖')
kde=stats.kde.gaussian_kde(sample_mean)
x=np.linspace(bins[0],bins[-1],100)
pl.plot(x,kde(x),label=u'核密度估計')
mean,std=stats.norm.fit(sample_mean)
pl.plot(x,stats.norm(mean,std).pdf(x),alpha=0.8,label=u'正態(tài)分布擬合')
pl.legend()
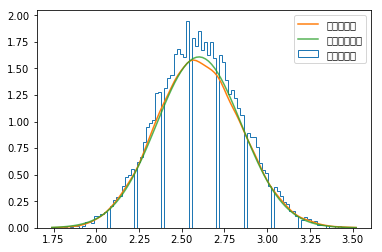
核密度估計算法是每個數(shù)據(jù)點放置一條核函數(shù)曲線,最終的核密度估計就是所有這些核函數(shù)曲線的疊加,gaussian_kde()的核函數(shù)為高斯曲線,其中bw_method參數(shù)決定了核函數(shù)的寬度,即高斯曲線的方差。bw_method參數(shù)可以是以下幾種情形:
當(dāng)為'scott','silverman'時將采用相應(yīng)的公式根據(jù)數(shù)據(jù)個數(shù)和維數(shù)決定核函數(shù)的寬度系數(shù) 當(dāng)為函數(shù)時,將調(diào)用此函數(shù)計算曲線寬度系數(shù),函數(shù)的參數(shù)為gaussian_kde對象 當(dāng)為數(shù)值時,將直接使用該數(shù)值作為寬度系數(shù)
核函數(shù)的方差由數(shù)據(jù)的方差和寬度系數(shù)決定
for?bw?in?[0.2,0.1]:
????kde=stats.gaussian_kde([-1,0,1],bw_method=bw)
????x=np.linspace(-5,5,1000)
????y=kde(x)
????pl.plot(x,y,lw=2,label='bw={}'.format(bw),alpha=0.6)
pl.legend(loc='best')
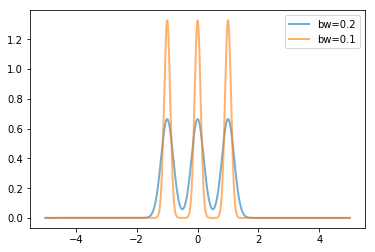
二項分布,泊松分布,伽馬分布
二項分布
from?scipy?import?stats
stats.binom.pmf(range(6),5,1/6.0)
array([4.01877572e-01, 4.01877572e-01, 1.60751029e-01, 3.21502058e-02,
3.21502058e-03, 1.28600823e-04])
該結(jié)果分別表示出現(xiàn)每個數(shù)1-5次的概率
泊松分布
import?numpy?as?np
import?matplotlib.pyplot?as?pl
lambda_=10.0
x=np.arange(20)
n1,n2=100,1000
y_binom_n1=stats.binom.pmf(x,n1,lambda_/n1)
y_binom_n2=stats.binom.pmf(x,n2,lambda_/n2)
y_possion=stats.poisson.pmf(x,lambda_)
pl.plot(x,y_binom_n1,label='n=100')
pl.plot(x,y_binom_n2,label='n=1000')
pl.plot(x,y_possion,label='possion')
pl.legend(loc="best")
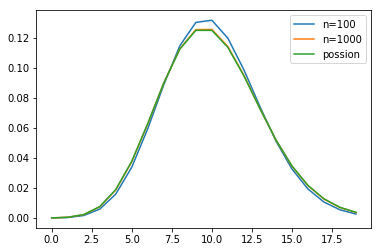
二項分布足夠大時,將會無限接近泊松分布
伽馬分布
觀察相鄰兩個事件之間的時間間隔的分布情況,或者隔k個時間的時間間隔的分布情況,根據(jù)概率論,事件之間的間隔應(yīng)該符合伽馬分布,由于時間間隔可以是任意數(shù)值的,因此伽馬分布是連續(xù)分布。
def?sim_gamma(lambda_,time,k):
????t=np.random.uniform(0,time,size=time*lambda_)
????t.sort()
????interval=t[k:]-t[:-k]
????dist,interval_edges=np.histogram(interval,bins=100,density=True)
????x=(interval_edges[1:]+interval_edges[:-1])/2
????gamma=stats.gamma.pdf(x,k,scale=1.0/lambda_)
????return?x,gamma,dist
lambda_=10
time=1000
ks=1,2
x1,gamma1,dist1=sim_gamma(lambda_,time,ks[0])
x2,gamma2,dist2=sim_gamma(lambda_,time,ks[1])
學(xué)生分布(t-分布)和t檢驗
從均值為的正態(tài)分布中,抽取有n個值的樣本,計算樣本均值和樣本方差s
則符合df=n-1的學(xué)生t分布,t值是抽選的樣本的平均值與整體樣本的期望值之差經(jīng)過正規(guī)化之后的數(shù)值,可以用來描述抽取的樣本與整體樣本之間的差異
mu=0.0
n=10
samples=stats.norm(mu).rvs(size=(10000,n))
t_samples=(np.mean(samples,axis=1)-mu)/np.std(samples,ddof=1,axis=1)*n**0.5
sample_dist,x=np.histogram(t_samples,bins=100,density=True)
x=0.5*(x[:-1]+x[1:])
t_dist=stats.t(n-1).pdf(x)
print("max_error:",np.max(np.abs(sample_dist-t_dist)))
max_error: 0.03503995452176545
使用t檢驗來檢驗零假設(shè)
n=30
np.random.seed(42)
s=stats.norm.rvs(loc=1,scale=0.8,size=n)
t=(np.mean(s)-0.5)/np.std(s,ddof=1)*n**0.5
print(t,stats.ttest_1samp(s,0.5))
2.658584340882224 Ttest_1sampResult(statistic=2.658584340882224, pvalue=0.01263770225709123)
ttest_lsamp返回的第一個是t值,第二個是p值
卡方分布和卡方檢驗
卡方分布是概率論和統(tǒng)計學(xué)中常用的一種概率分布,K個獨立的標(biāo)準(zhǔn)正態(tài)分布變量的平方和服從自由度為k的卡方分布。
a=np.random.normal(size=(300000,4))
cs=np.sum(a**2,axis=1)
sample_dist,bins=np.histogram(cs,bins=100,range=(0,20),density=True)
x=0.5*(bins[:-1]+bins[1:])#求分組區(qū)間的均值
chi2_dist=stats.chi2.pdf(x,4)
print("max_error:",np.max(np.max(sample_dist-chi2_dist)))
max_error: 0.0026251381501953552
卡方檢驗
def?choose_ball(ps,size):
????r=stats.rv_discrete(values=(range(len(ps)),ps))
????s=r.rvs(size=size)
????counts=np.bincount(s)
????return?counts
np.random.seed(42)
counts1=choose_ball([0.18,0.24,0.25,0.16,0.17],400)
counts2=choose_ball([0.2]*5,400)
chi1,p1=stats.chisquare(counts1)
chi2,p2=stats.chisquare(counts2)
print('chi1={},p1={}'.format(chi1,p1))
print('chi2={},p2={}'.format(chi2,p2))
chi1=11.375,p1=0.022657601239769634
chi2=2.55,p2=0.6357054527037017
數(shù)值積分
球的體積
def?half_circle(x):
????return?(1-x**2)**0.5
def?half_sphere(x,y):
????return?(1-x**2-y**2)**0.5
from?scipy?import?integrate
pi_half,err=integrate.quad(half_circle,-1,1)
s=pi_half*2
print('圓面積為:',s)
volume,err=integrate.dblquad(half_sphere,-1,1,lambda?x:-half_circle(x),lambda?x:half_circle(x))#后面兩個lambda函數(shù)指定y的取值范圍
print("體積為",volume)
圓面積為:3.141592653589797
體積為 2.094395102393199
解常微分方程
integrate模塊還提供了對常微分方程組進行積分的函數(shù)odeint(),下面講解如果用odeint()計算洛倫茨吸引子的軌跡,洛倫茨吸引子由下面的三個微分方程定義
odeint()有許多的參數(shù),這里用到的4個參數(shù)主要是:
lorenz:它是計算某個位置上的各個方向的速度的函數(shù) (x,y,z):位置初始值,他是計算常微分方程所需的各個變量的初始值 t:表示時間的數(shù)組,odeint()對此數(shù)組中的每個時間點進行求解,得出所有時間點的位置 args:這些參數(shù)直接傳遞給lorenz,因此他們在整個積分過程中都是常量
from?scipy.integrate?import?odeint
def?lorenz(w,t,p,r,b):
????#給出位置矢量w和三個參數(shù)p,r,b
????#計算出dx/dt,dy/dt,dz/dt的值
????x,y,z=w.tolist()
????#直接與洛倫茲公式對應(yīng)
????return?p*(y-x),x*(r-z)-y,x*y-b*z
t=np.arange(0,30,0.02)#創(chuàng)建時間點
#調(diào)用ode對lorenz求解
track1=odeint(lorenz,(0.0,1.00,0.0),t,args=(10.0,28.0,3.0))
track2=odeint(lorenz,(0.0,1.01,0.0),t,args=(10.0,28.0,3.0))
ode類
使用odeint()可以很方便的計算微分方程組的數(shù)值解,只需要調(diào)用一次odeint()就能計算出一組時間點上的系統(tǒng)狀態(tài)。
def?mass_spring_damper(xu,t,m,k,b,F):
????x,u=xu.tolist()
????dx=u
????du=(F-k*x-b*u)/m
????return?dx,du
m,b,k,F=1.0,10.0,20.0,1.0
args=m,b,k,F
init_status=0.0,0.0
t=np.arange(0,2,0.02)
result=odeint(mass_spring_damper,init_status,t,args)
參考
[1]《Data Science Application with Scipy》
