一文講透神經(jīng)網(wǎng)絡(luò)的激活函數(shù)

為什么要激活函數(shù)？

原理上來說，神經(jīng)網(wǎng)絡(luò)模型的訓(xùn)練過程其實就是擬合一個數(shù)據(jù)分布（x）可以映射到輸出（y）的數(shù)學(xué)函數(shù)，即 y= f(x)。

擬合效果的好壞取決于數(shù)據(jù)質(zhì)量及模型的結(jié)構(gòu)，像邏輯回歸、感知機(jī)等線性模型的擬合能力是有限的，連xor函數(shù)都擬合不了，那神經(jīng)網(wǎng)絡(luò)模型結(jié)構(gòu)中提升擬合能力的關(guān)鍵是什么呢？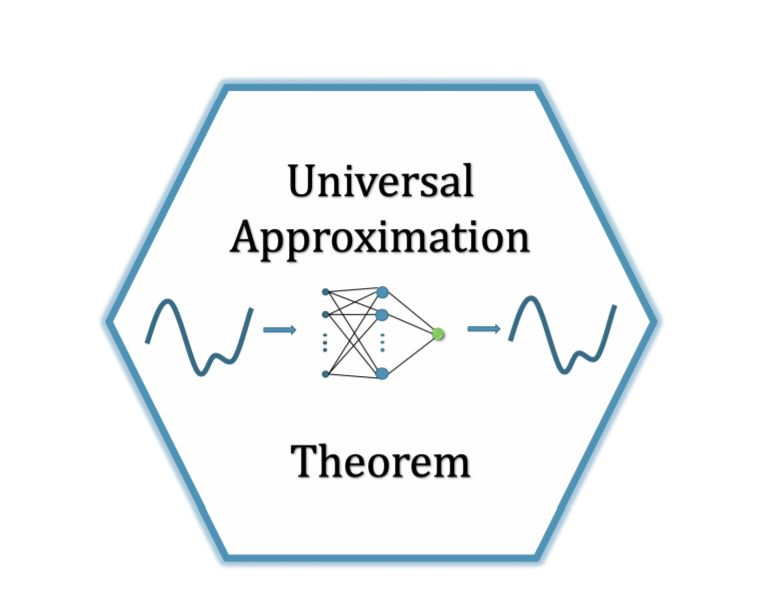

搬出神經(jīng)網(wǎng)絡(luò)的萬能近似定理可知，“一個前饋神經(jīng)網(wǎng)絡(luò)如果具有線性輸出層和至少一層具有任何一種‘‘?dāng)D壓’’ 性質(zhì)的激活函數(shù)的隱藏層，只要給予網(wǎng)絡(luò)足夠數(shù)量的隱藏單元，它可以以任意的精度來近似任何從一個有限維空間到另一個有限維空間的Borel可測函數(shù)。”簡單來說，前饋神經(jīng)網(wǎng)絡(luò)有“夠深的網(wǎng)絡(luò)層”以及“至少一層帶激活函數(shù)的隱藏層”，既可以擬合任意的函數(shù)。

在此激活函數(shù)起的作用是實現(xiàn)特征空間的非線性轉(zhuǎn)換，貼切的來說是，“數(shù)值上擠壓，幾何上變形”。如下圖，在帶激活函數(shù)的隱藏層作用下，可以對特征空間進(jìn)行轉(zhuǎn)換，最終使得數(shù)據(jù)（紅色和藍(lán)色線表示的樣本）線性可分。而如果網(wǎng)絡(luò)沒有激活函數(shù)的隱藏層（僅有線性隱藏層），以3層的神經(jīng)網(wǎng)絡(luò)為例，可得第二層輸出為：

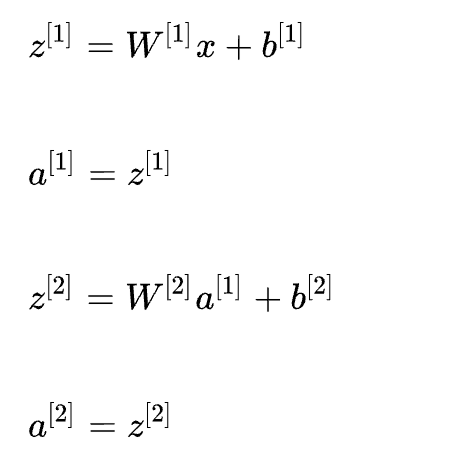
對上式中第二層的輸出a^[2]進(jìn)行化簡計算

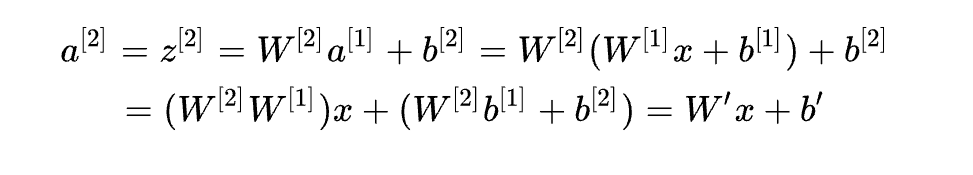
可見無論神經(jīng)網(wǎng)絡(luò)有多少層，輸出都是輸入x的線性組合，多層線性神經(jīng)網(wǎng)絡(luò)本質(zhì)上還是線性模型，而其轉(zhuǎn)換后的特征空間還是線性不可分的。

如何選擇合適的激活函數(shù)？

如果一個函數(shù)能提供非線性轉(zhuǎn)換（即導(dǎo)數(shù)不恒為常數(shù)），可導(dǎo)（可導(dǎo)是從梯度下降方面考慮。可以有一兩個不可導(dǎo)點, 但不能在一段區(qū)間上都不可導(dǎo)）等性質(zhì)，即可作為激活函數(shù)。在不同網(wǎng)絡(luò)層（隱藏層、輸出層）的激活函數(shù)關(guān)注的重點不一樣，隱藏層關(guān)注的是計算過程的特性，輸出層關(guān)注的輸出個數(shù)及數(shù)值范圍。

那如何選擇合適的激活函數(shù)呢？這是結(jié)合不同激活函數(shù)的特點的實證過程。

• sigmoid 與 tanh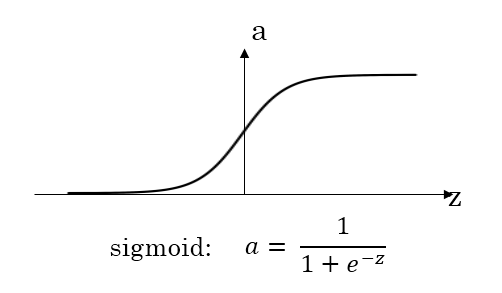

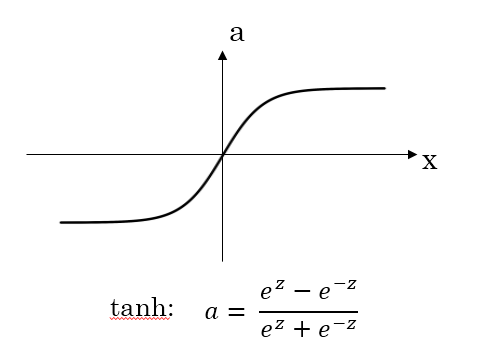
從函數(shù)圖像上看，tanh函數(shù)像是伸縮過的sigmoid函數(shù)然后向下平移了一格，確實就是這樣，因為它們的關(guān)系就是線性關(guān)系。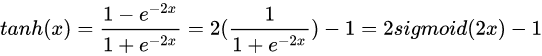對于隱藏層的激活函數(shù)，一般來說，tanh函數(shù)要比sigmoid函數(shù)表現(xiàn)更好一些。

因為tanh函數(shù)的取值范圍在[-1,+1]之間，隱藏層的輸出被限定在[-1,+1]之間，可以看成是在0值附近分布，均值為0。這樣從隱藏層到輸出層，數(shù)據(jù)起到了歸一化（均值為0）的效果。

另外，由于Sigmoid函數(shù)的輸出不是零中心的（Zero-centered），該函數(shù)的導(dǎo)數(shù)為：sigmoid * (1 - sigmoid)，如果輸入x都是正數(shù)，那么sigmoid的輸出y在[0.5，1]。那么sigmoid的梯度 = [0.5, 1] * (1 - [0.5, 1]) ~= [0, 0.5] 總是 > 0的。假設(shè)最后整個神經(jīng)網(wǎng)絡(luò)的輸出是正數(shù)，最后 w 的梯度就是正數(shù)；反之，假如輸入全是負(fù)數(shù)，w 的梯度就是負(fù)數(shù)。這樣的梯度造成的問題就是，優(yōu)化過程呈現(xiàn)“Z字形”（zig-zag），因為w 要么只能往下走（負(fù)數(shù)），要么只能往右走（正的），導(dǎo)致優(yōu)化的效率十分低下。而tanh就沒有這個問題。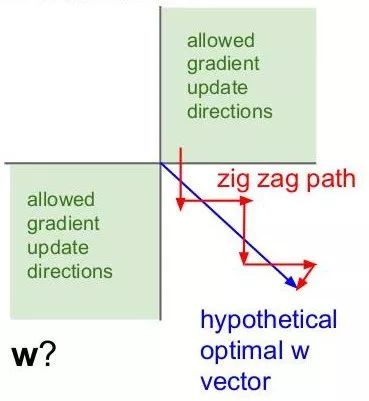

對于輸出層的激活函數(shù)，因為二分類問題的輸出取值為{0,+1}，所以一般會選擇sigmoid作為激活函數(shù)。另外，sigmoid天然適合做概率值處理，例如用于LSTM中的門控制。

觀察sigmoid函數(shù)和tanh函數(shù)，我們發(fā)現(xiàn)有這樣一個問題，就是當(dāng)|z|很大的時候，激活函數(shù)的斜率（梯度）很小。在反向傳播的時候，這個梯度將會與整個損失函數(shù)關(guān)于該神經(jīng)元輸出的梯度相乘，那么相乘的結(jié)果也會接近零，這會導(dǎo)致梯度消失；同樣的，當(dāng)z落在0附近，梯度是相當(dāng)大的，梯度相乘就會出現(xiàn)梯度爆炸的問題（一般可以用梯度裁剪即Gradient Clipping來解決梯度爆炸問題）。由于其梯度爆炸、梯度消失的缺點，會使得網(wǎng)絡(luò)變的很難進(jìn)行學(xué)習(xí)。

• ReLU 與 leaky ReLU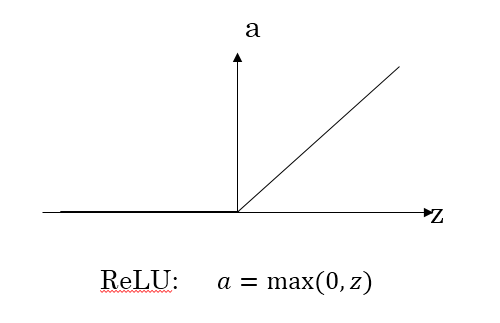
  

為了彌補(bǔ)sigmoid函數(shù)和tanh函數(shù)的缺陷，就出現(xiàn)了ReLU激活函數(shù)。ReLU激活函數(shù)求導(dǎo)不涉及浮點運算，所以速度更快。在z大于零時梯度始終為1；在z小于零時梯度始終為0；z等于零時的梯度可以當(dāng)成1也可以當(dāng)成0，實際應(yīng)用中并不影響。對于隱藏層，選擇ReLU作為激活函數(shù)，能夠保證z大于零時梯度始終為1，從而提高神經(jīng)網(wǎng)絡(luò)梯度下降算法運算速度。

而當(dāng)輸入z小于零時，ReLU存在梯度為0的特點，一旦神經(jīng)元的激活值進(jìn)入負(fù)半?yún)^(qū)，那么該激活值就不會產(chǎn)生梯度/不會被訓(xùn)練，雖然減緩了學(xué)習(xí)速率，但也造成了網(wǎng)絡(luò)的稀疏性——稀疏激活，這有助于減少參數(shù)的相互依賴，緩解過擬合問題的發(fā)生。

對于上述問題，也就有了leaky ReLU，它能夠保證z小于零是梯度不為0，可以改善RELU導(dǎo)致神經(jīng)元稀疏的問題而提高學(xué)習(xí)速率。但是缺點也很明顯，因為有了負(fù)數(shù)的輸出，導(dǎo)致其非線性程度沒有RELU強(qiáng)大，在一些分類任務(wù)中效果還沒有Sigmoid好，更不要提ReLU。（此外ReLU還有很多變體RReLU、PReLU、SELU等，可以自行擴(kuò)展）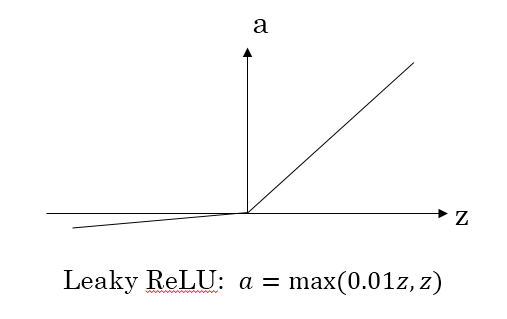

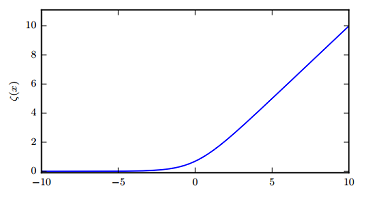
• softplus：

softplus 是 ReLU 的平滑版本，也就是不存在單點不可導(dǎo)。但根據(jù)實際經(jīng)驗來看，并沒什么效果，ReLU的結(jié)果是更好的。

• Swish

swish函數(shù)又叫作自門控激活函數(shù)，它近期由谷歌的研究者發(fā)布，數(shù)學(xué)公式為：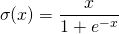

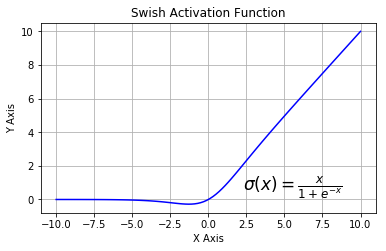
和 ReLU 一樣，Swish 無上界有下界。與 ReLU 不同的是，Swish 有平滑且非單調(diào)的特點。根據(jù)論文（https://arxiv.org/abs/1710.05941v1），Swish 激活函數(shù)的性能優(yōu)于 ReLU 函數(shù)。

• Maxout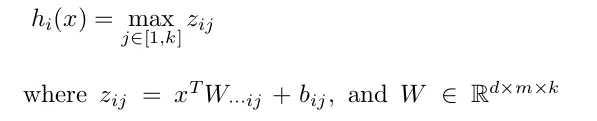

maxout 進(jìn)一步擴(kuò)展了 ReLU，它是一個可學(xué)習(xí)的 k 段函數(shù)。它具有如下性質(zhì)：

1、maxout激活函數(shù)并不是一個固定的函數(shù)，不像Sigmod、Relu、Tanh等固定的函數(shù)方程

2、它是一個可學(xué)習(xí)的激活函數(shù)，因為w參數(shù)是學(xué)習(xí)變化的。

3、它是一個分(k)段線性函數(shù)：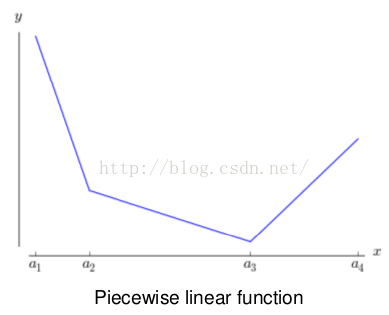

#?Keras?簡單實現(xiàn)Maxout

#?input?shape:??[n,?input_dim]
#?output?shape:?[n,?output_dim]
W?=?init(shape=[k,?input_dim,?output_dim])
b?=?zeros(shape=[k,?output_dim])
output?=?K.max(K.dot(x,?W)?+?b,?axis=1)

• RBF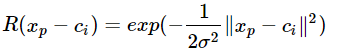徑向基函數(shù)關(guān)于n維空間的一個中心點具有徑向?qū)ΨQ性，而且神經(jīng)元的輸入離該中心點越遠(yuǎn)，神經(jīng)元的激活程度就越低（值越接近0），在神經(jīng)網(wǎng)絡(luò)中很少使用徑向基函數(shù)（radial basis function, RBF）作為激活函數(shù)，因為它對大部分 x 都飽和到 0，所以很難優(yōu)化。

#?Keras?簡單實現(xiàn)RBF
from?keras.layers?import?Layer
from?keras?import?backend?as?K

class?RBFLayer(Layer):
????def?__init__(self,?units,?gamma,?**kwargs):
????????super(RBFLayer,?self).__init__(**kwargs)
????????self.units?=?units
????????self.gamma?=?K.cast_to_floatx(gamma)

????def?build(self,?input_shape):
????????self.mu?=?self.add_weight(name='mu',
??????????????????????????????????shape=(int(input_shape[1]),?self.units),
??????????????????????????????????initializer='uniform',
??????????????????????????????????trainable=True)
????????super(RBFLayer,?self).build(input_shape)

????def?call(self,?inputs):
????????diff?=?K.expand_dims(inputs)?-?self.mu
????????l2?=?K.sum(K.pow(diff,2),?axis=1)
????????res?=?K.exp(-1?*?self.gamma?*?l2)
????????return?res

????def?compute_output_shape(self,?input_shape):
????????return?(input_shape[0],?self.units)

#?用法示例:
model?=?Sequential()
model.add(Dense(20,?input_shape=(100,)))
model.add(RBFLayer(10,?0.5))

• softmax

softmax 函數(shù)，也稱歸一化指數(shù)函數(shù)，常作為網(wǎng)絡(luò)的輸出層激活函數(shù)，它很自然地輸出表示具有 n個可能值的離散型隨機(jī)變量的概率分布。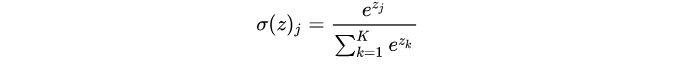數(shù)學(xué)函數(shù)式如上，公式引入了指數(shù)可以擴(kuò)大類間的差異。

經(jīng)驗性的總結(jié)

對于是分類任務(wù)的輸出層，二分類的輸出層的激活函數(shù)常選擇sigmoid函數(shù)，多分類選擇softmax；回歸任務(wù)根據(jù)輸出值確定激活函數(shù)或者不使用激活函數(shù)；對于隱藏層的激活函數(shù)通常會選擇使用ReLU函數(shù)，保證學(xué)習(xí)效率。其實，具體選擇哪個函數(shù)作為激活函數(shù)沒有一個固定的準(zhǔn)確的答案，應(yīng)該要根據(jù)具體實際問題進(jìn)行驗證（validation）。