LWN:Julia 中的并發(fā)處理!
關(guān)注了就能看到更多這么棒的文章哦~
Concurrency in Julia
November 9, 2021
This article was contributed by Lee Phillips
DeepL assisted translation
https://lwn.net/Articles/875367/
Julia 編程語(yǔ)言起源于高性能科學(xué)計(jì)算領(lǐng)域,所以它自然會(huì)很好地支持擁有并發(fā)處理(concurrent processing)。不過(guò),這些功能在 Julia 社區(qū)之外并沒(méi)有多少人知道,所以很值得介紹一下該語(yǔ)言所支持的不同類型的并行(parallel)和并發(fā)(concurrent)計(jì)算。此外,即將發(fā)布的 Julia 1.7 版本為該語(yǔ)言的并發(fā)計(jì)算功能又帶來(lái)了一塊補(bǔ)充,也就是 "任務(wù)遷移(task migration)"。
Multithreading
Julia 支持各種形式的并發(fā)計(jì)算。多線程計(jì)算(a multithreaded computation)就是一種在不同的處理單元上同時(shí)進(jìn)行工作的一種并發(fā)計(jì)算。多線程以及與此相關(guān)的術(shù)語(yǔ)并行計(jì)算(parallel computation),通常意味著各個(gè)線程都可以訪問(wèn)相同的主內(nèi)存區(qū)域(main memory),因此它會(huì)用到同一臺(tái)計(jì)算機(jī)上的多個(gè) CPU core 或處理單元。
Julia 啟動(dòng)時(shí)如果沒(méi)有帶 -t 標(biāo)志,那么就只會(huì)使用一個(gè)線程。要想讓它利用所有可用的硬件線程(hardware thread),就可以使用 -t auto 這個(gè)參數(shù)。這會(huì)讓它利用機(jī)器上所有的邏輯線程(logic threads)。不過(guò)這通常不是最好的選擇,還是應(yīng)該盡量用 -t n,其中 n 是物理 CPU core 的數(shù)量。例如,流行的英特爾酷睿處理器為每個(gè)物理核心提供了兩個(gè)邏輯核心,使用了一種叫做超線程(hyperthreading)的技術(shù)實(shí)現(xiàn)倍增效果,在不同類型的計(jì)算中,這個(gè)特性可能有的會(huì)導(dǎo)致一些性能提升,有的則會(huì)降低一些性能。
為了演示 Julia 的多線程,我們將使用下面的函數(shù),來(lái)檢測(cè)一個(gè)數(shù)字是否為素?cái)?shù)(prime)。本文中的例子代碼都去掉了一些可能的優(yōu)化方式,為了簡(jiǎn)化代碼便于理解,isprime() 函數(shù)就是采用這個(gè)原則寫出的:
function isprime(x::Int)
if x < 2
return false
end
u = isqrt(x) # integer square root
for n in 2:u
if x % n == 0
return false
end
end
return true
end
function isprime(x::Any)
return "Integers only, please"
end
這個(gè)函數(shù)應(yīng)該只檢查整數(shù)(Int 是 Int64 的別名),所以我們利用了多重派發(fā)(multi dispatch)來(lái)創(chuàng)建了兩個(gè)函數(shù)(method):一個(gè)用來(lái)檢查是不是素?cái)?shù),另一個(gè)函數(shù)則是用來(lái)在收到不是整數(shù)的數(shù)據(jù)的時(shí)候給出錯(cuò)誤信息。每次都會(huì)根據(jù)最合適的類型來(lái)選擇調(diào)用哪個(gè)函數(shù),因此我們就可以不用在函數(shù)內(nèi)部顯式地寫出類型檢測(cè)代碼,就可以把不正確的數(shù)據(jù)類型預(yù)先處理掉。
在我的測(cè)試中有一個(gè)很好用的多線程軟件包,名為 Folds。這不是標(biāo)準(zhǔn)庫(kù)中的軟件包,所以你必須使用 Julia 的軟件包管理工具先安裝好。Folds 包提供了若干用于并發(fā)處理的 high-level 的宏和函數(shù)。它的名字意思是 "折疊",也就意味著是用來(lái)簡(jiǎn)化數(shù)組的(reduction over an array)。Folds 提供了 map()、sum()、maximum()、minimum()、reduce()、collect() 等函數(shù)的多線程版本實(shí)現(xiàn),以及其他一些對(duì) collection (集合)的自動(dòng)并行處理的支持。
這里我們使用 map() 來(lái)檢查一系列數(shù)字是否為素?cái)?shù)。如果 f() 是帶有一個(gè)變量的函數(shù),而 A 是一個(gè)數(shù)組,那么表達(dá)式 map(f, A) 就會(huì)對(duì) A 的每個(gè)元素分別調(diào)用 f(),然后返回一個(gè)與 A 的個(gè)數(shù)相同的數(shù)組。用多線程操作來(lái)替換 map() 就是下面這么簡(jiǎn)單:
julia> @btime map(isprime, 1000:9999999);
8.631 s (2 allocations: 9.54 MiB)
julia> @btime Folds.map(isprime, 1000:9999999);
5.406 s (45 allocations: 29.48 MiB)
在 Julia 中,a:n:b 這種寫法就定義了一個(gè)名為 "range" 的迭代器(iterator),它會(huì)從 a 到 b 按 n(默認(rèn)為 1)這個(gè)步長(zhǎng)來(lái)遞增。在調(diào)用 map() 的時(shí)候,這些 range 就會(huì)被當(dāng)作一個(gè) vector。
Folds.map() 將數(shù)組分成相同長(zhǎng)短的多個(gè)段(segments),給每個(gè)線程都分配一個(gè) segment,并在每個(gè) segment 上并行執(zhí)行 map()操作。與本文中的所有實(shí)驗(yàn)一樣,耗時(shí)統(tǒng)計(jì)都是使用 Julia 1.7rc1 版本來(lái)進(jìn)行的。在這個(gè)測(cè)試中,我啟動(dòng) REPL 的命令是 julia -t2。
BenchmarkTools 軟件包中提供的 @btime 宏,會(huì)對(duì)后面的任務(wù)執(zhí)行數(shù)次,然后報(bào)告出平均運(yùn)行時(shí)間。時(shí)間顯示,在我的雙核機(jī)器上,運(yùn)行速度與理想值也就是 2 倍來(lái)說(shuō)相差不大,但代價(jià)是消耗了更多的內(nèi)存。CPU 使用率的分析也證實(shí)了在第一次計(jì)算時(shí)只有一個(gè) CPU core 在工作,而第二次計(jì)算時(shí)就有兩個(gè) core 來(lái)忙于處理了。
多線程處理的另一種方式是使用圖形處理單元(GPU,graphics processing units)。GPU 最初是為了加速 3D 游戲和其他重度圖形應(yīng)用中都帶有的那些并行圖形計(jì)算(parallel graphics calculations)而設(shè)計(jì)的,它擁有數(shù)百或數(shù)千個(gè)浮點(diǎn)處理器,這些現(xiàn)在都可以作為陣列協(xié)處理器(array coprocessors)來(lái)用在各種應(yīng)用中。GPU 計(jì)算的最佳對(duì)象就是那些算術(shù)操作和內(nèi)存操作比例占比很高的并行計(jì)算。有一個(gè)名為 JuliaGPU 的組織,就提供了許多實(shí)現(xiàn)或依賴這種并行處理方式的 Julia 軟件包。
map 操作本質(zhì)上就是并行進(jìn)行的,它會(huì)把某個(gè)函數(shù)獨(dú)立地作用于集合中的每個(gè)元素,既不會(huì)從其他元素中讀取,也不會(huì)向其他元素進(jìn)行寫入。正因?yàn)槿绱耍瑐鹘y(tǒng)的 map 可以替換成多線程版本的實(shí)現(xiàn),不會(huì)改變程序中的其他內(nèi)容。也不會(huì)出現(xiàn)那些同時(shí)訪問(wèn)同一數(shù)據(jù)這類復(fù)雜問(wèn)題。
而現(xiàn)實(shí)生活中的程序都會(huì)包含一些容易并行化的部分,也同時(shí)包含一些需要小心處理的部分,還有一些完全不能并行化的部分。比如來(lái)討論一下簡(jiǎn)單的星系模擬的工作,多個(gè)星體在相互引力的影響下運(yùn)動(dòng)。每個(gè)物體上受到的力都必須要先檢查所有其他物體的位置來(lái)計(jì)算得出(超出一定距離可以忽略,具體取決于最終的精度要求)。盡管這部分計(jì)算可以并行化,但這就比上面討論的 map() 操作更加復(fù)雜了。但是在將來(lái)自各個(gè)位置的受力存儲(chǔ)下來(lái)之后,每個(gè)物體的速度變化就可以獨(dú)立于其他物體來(lái)計(jì)算出來(lái)了,這可以利用一個(gè)簡(jiǎn)單的 map() 結(jié)構(gòu)來(lái)很容易進(jìn)行并行化計(jì)算。
Julia 就具有所有那些用在更復(fù)雜的場(chǎng)景下的并發(fā)計(jì)算的支持。使用 @threads 宏就可以使一個(gè) for 循環(huán)成為多線程的的實(shí)現(xiàn):
Threads.@threads for i = 1:N
end
在這種情況下,假如我們有兩個(gè)線程,其中一個(gè)線程會(huì)從 1 到 N/2 來(lái)進(jìn)行循環(huán),另一個(gè)線程是從 N/2 到 N 進(jìn)行循環(huán)。只要有多個(gè)線程需要訪問(wèn)到同一個(gè)數(shù)據(jù),那么這些數(shù)據(jù)就必須用鎖來(lái)保護(hù)起來(lái),這個(gè)功能是由 lock()函數(shù)來(lái)提供的。Julia 也支持使用 Atomic 數(shù)據(jù)類型來(lái)防止一些 race condition (競(jìng)態(tài)問(wèn)題)。程序不可以簡(jiǎn)單地修改這種類型的數(shù)據(jù),除非是使用比如 Threads.atomic_add!()和 Threads.atomic_sub!() 這樣的原子操作來(lái)代替正常的加法和減法。
Distributed processing
另一種類型的并發(fā)則牽涉到多個(gè)配合起來(lái)的異步任務(wù) coroutines,Julia 稱之為 Tasks。這些程序可以共享同一個(gè)線程、或者分發(fā)給多個(gè)線程、被分發(fā)到集群中的不同節(jié)點(diǎn)上、甚至分發(fā)到互聯(lián)網(wǎng)上位于不同位置的分布式系統(tǒng)上。所有這些形式的分布式計(jì)算(distributed computing)都有一個(gè)共同的特點(diǎn):處理器不可以直接訪問(wèn)到相同的內(nèi)存位置,所以數(shù)據(jù)必須要被傳送到需要對(duì)其進(jìn)行計(jì)算的地方。
tasks 很適合這樣的場(chǎng)景:程序需要耗費(fèi)一些時(shí)間來(lái)啟動(dòng)一個(gè)工作,但這個(gè)程序可以繼續(xù)執(zhí)行,因?yàn)樗⒉恍枰⒓吹玫侥莻€(gè)工作的計(jì)算結(jié)果。例如從互聯(lián)網(wǎng)上下載數(shù)據(jù)、復(fù)制文件、或者執(zhí)行一個(gè)長(zhǎng)期運(yùn)行的計(jì)算而之后才需要其計(jì)算結(jié)果。
當(dāng)用 -p n 標(biāo)志調(diào)用 Julia 時(shí),除了主執(zhí)行進(jìn)程外,還會(huì)初始化出 n 個(gè)工作進(jìn)程(executive process)。這兩個(gè)多進(jìn)程標(biāo)志(multiprocessing flags)可以結(jié)合起來(lái)使用,如 julia -p2 -t2。這就會(huì)啟動(dòng)兩個(gè)工作進(jìn)程,每個(gè)進(jìn)程可以使用兩個(gè)線程來(lái)進(jìn)行計(jì)算。在本節(jié)的例子中,我使用 julia -p2。
"手動(dòng)" 地啟動(dòng)一個(gè) task,就是使用 @spawnat :any expr 這個(gè)宏調(diào)用方式。其指定了一個(gè) task 來(lái)計(jì)算 expr 這個(gè)表達(dá)式,會(huì)使用系統(tǒng)所選擇的那個(gè)工作進(jìn)程來(lái)計(jì)算。工作進(jìn)程是從 1 開(kāi)始的整數(shù)標(biāo)識(shí)符,在 :any 這個(gè)位置使用一個(gè)整數(shù)來(lái)代替的話,就會(huì)讓 task 在該特定進(jìn)程中孵化運(yùn)行。
常見(jiàn)做法是使用 pmap() 這個(gè)分布式版本的 map() 操作,其會(huì)由 -p 參數(shù)來(lái) import 進(jìn)來(lái),也會(huì)進(jìn)行相同的計(jì)算工作,但是首先會(huì)將數(shù)組分解成若干部分,向每個(gè)工作進(jìn)程發(fā)送相同大小的一部分,由其來(lái)并行執(zhí)行 map 操作,然后收集和匯總結(jié)果。舉個(gè)例子,下面是使用著名的收斂非常緩慢的萊布尼茲和方式來(lái)估算 π(見(jiàn)下圖)。
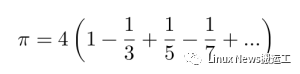
[萊布尼茲求和方程]
函數(shù) leibniz(first, last, nterms) 會(huì)返回一個(gè)數(shù)組,其中包含前兩個(gè)參數(shù)之間的每一個(gè) nterms 項(xiàng)的結(jié)果:
@everywhere function leibniz(first, last, nterms)
r = []
for i in first:nterms:last # Step from first to last by nterms
i1 = i
i2 = i+nterms-1
# Append the next partial sum to r:
push!(r, (i1, i2, 4*sum((-1)^(n+1) * 1/(2n-1) for n in i1:i2)))
end
return r
end
@everywhere 宏也是由-p 標(biāo)志 import 進(jìn)來(lái)的,它會(huì)將函數(shù)和變量的定義廣播給所有的工作進(jìn)程。這是一個(gè)必要工作,因?yàn)楣ぷ鬟M(jìn)程與主進(jìn)程并沒(méi)有共享內(nèi)存。leibniz()函數(shù)是 Leibniz sum 的簡(jiǎn)單翻譯出來(lái)的版本,其會(huì)用 sum() 函數(shù)將生成器表達(dá)式(generator expression)中的項(xiàng)加起來(lái)。在每一組 nterms 項(xiàng)之后,會(huì)將累積的部分結(jié)果放入 r 數(shù)組,完成后將此數(shù)組返回回去。
為了測(cè)試 pmap()的性能,我們可以用它來(lái)同時(shí)計(jì)算前 2×108?項(xiàng):
julia> @btime r = pmap(n -> leibniz(n, n+10^8-1, 1000), [1, 10^8+1]);
7.127 s (1600234 allocations: 42.21 MiB)
使用普通 map 的版本,只用了一個(gè)進(jìn)程,就需要幾乎兩倍的時(shí)間(但只使用了 23%的內(nèi)存)。
julia> @btime r = map(n -> leibniz(n, n+10^8-1, 1000), [1, 10^8+1]);
13.630 s (200024 allocations: 9.76 MiB)
下圖是對(duì)萊布尼茲數(shù)列的前 2×108 項(xiàng)求和的結(jié)果。
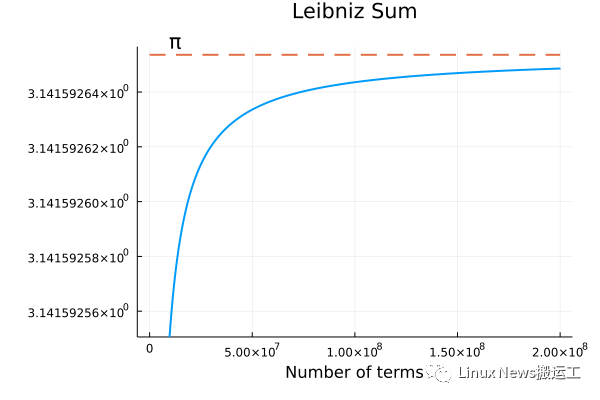
[萊布尼茲求和收斂]
這個(gè)分布式處理的版本比起普通 map() 操作消耗了多得多的內(nèi)存空間,這也是我在大多數(shù)場(chǎng)合都觀察到的情況。pmap() 看起來(lái)最適合那些粗粒度的多任務(wù)處理(coarse-grained multiprocessing),它是一種對(duì)小范圍的輸入集合(a small collection of inputs)的耗時(shí)操作有效進(jìn)行加速的處理方法。
Julia 的分布式處理機(jī)制也可以跨越多個(gè)機(jī)器。當(dāng)給定了一個(gè)文件中含有各個(gè)互聯(lián)網(wǎng) IP 地址時(shí),Julia 就會(huì)使用 SSH 和公鑰認(rèn)證來(lái)經(jīng)過(guò)互聯(lián)網(wǎng)生成 job,這樣就可以讓本地開(kāi)發(fā)出來(lái)的分布式代碼在配置好的計(jì)算機(jī)網(wǎng)絡(luò)上運(yùn)行了,只需進(jìn)行少量修改就好。
Tasks and task migration
Julia 支持的另一種并發(fā)處理可以被稱為 asynchronous multithreading (異步多線程)。它會(huì)使用 Julia tasks 來(lái)進(jìn)行計(jì)算,但會(huì)分配給一個(gè)進(jìn)程中的多個(gè)線程去執(zhí)行。因此所有的任務(wù)都可以訪問(wèn)到相同的內(nèi)存區(qū)域,合作來(lái)進(jìn)行多任務(wù)處理。在本節(jié)的例子中,我用 julia -t2 啟動(dòng)了 Julia,所以我的兩個(gè) CPU 核上各有一個(gè)線程。
我們可以通過(guò)一個(gè)宏來(lái)啟動(dòng)一個(gè)任務(wù)并將其自動(dòng)安排在一個(gè)可用的線程上:a = Threads.@spawn expr。這將返回一個(gè) Task 對(duì)象。我們調(diào)用 fetch(a) 就可以等待該 Task 完成并獲取 expr 的返回值。
對(duì)于一組運(yùn)行時(shí)間大致相等的 Task 的計(jì)算,基本可以看到執(zhí)行速度會(huì)與 CPU 線程的數(shù)量有接近線性的關(guān)系。在過(guò)去的 Julia 版本中,一旦某個(gè)任務(wù)被安排在一個(gè)線程上了,就會(huì)被卡在那里直到最終完成。這樣如果某些任務(wù)比其他任務(wù)需要更長(zhǎng)的時(shí)間,那么就可能會(huì)產(chǎn)生調(diào)度問(wèn)題,導(dǎo)致那些承載了任務(wù)較少的 Task 的線程可能就會(huì)變得很空閑,而任務(wù)較重的那些 Task 則繼續(xù)在它們?cè)瓉?lái)的線程上爭(zhēng)奪 CPU 時(shí)間。在這種涉及到運(yùn)行時(shí)間非常不平等的多個(gè) Task 的情況下,我們可能就看不到速度提升的線性關(guān)系了,因?yàn)橛匈Y源被浪費(fèi)了。
在 Julia 1.7 版本中,task 允許在線程之間遷移了。因此可以被重新安排到可用的線程上,而不是停留在它們最初被分配的線程。這項(xiàng)功能目前還缺乏文檔,但我使用 Threads.@spawn 啟動(dòng)的那些 task 可以在調(diào)用 yield() 時(shí)被遷移,yield() 函數(shù)的用途是暫停一個(gè) task 并允許另一個(gè)被調(diào)度到的 task 運(yùn)行。
為了能直接觀察到線程遷移的效果,我就需要能夠打開(kāi)和關(guān)閉這個(gè)功能。我們可以編譯一個(gè)沒(méi)有啟用該功能的 Julia 版本來(lái)進(jìn)行測(cè)試,但其實(shí)還有一個(gè)更簡(jiǎn)單的方法。ThreadPools 包提供了一組用于并發(fā)處理的宏。我在實(shí)驗(yàn)中使用了 @tspawnat 宏,用其產(chǎn)生的 task 都可以遷移,就像使用 Threads.@spawn 產(chǎn)生的任務(wù)一樣,但是使用@tspawnat 也允許我可以簡(jiǎn)單地修改來(lái)產(chǎn)生一個(gè)不允許遷移的 task。
Monte Carlo 物理模擬,或者概率建模(probabilistic modeling)都是異步多線程計(jì)算的理想場(chǎng)景。可以先運(yùn)行一組模擬(simulation),這些 simulation 中除了控制每個(gè)任務(wù)計(jì)算細(xì)節(jié)的一系列偽隨機(jī)數(shù)之外,其他都是完全一樣的。所有的任務(wù)都是相互獨(dú)立的,當(dāng)它們都完成之后就可以得到各種平均數(shù)及其數(shù)據(jù)的分布情況。
我在實(shí)驗(yàn)中寫了一個(gè)簡(jiǎn)單的程序來(lái)考察 Julia 的偽隨機(jī)數(shù)生成函數(shù) rand() 的統(tǒng)計(jì)特性,調(diào)用該函數(shù)會(huì)返回一個(gè)在 0 到 1 之間的均勻分布的隨機(jī)數(shù),而不需要任何參數(shù)。下面的函數(shù)每次調(diào)用時(shí)指定參數(shù) n,就會(huì)進(jìn)行 n 次生成一個(gè)隨機(jī)數(shù)的操作,并把數(shù)據(jù)分成 n/10 組,報(bào)告出每組數(shù)字的平均值:
function darts(n)
if n % 10 != 0 || n <= 0
return nothing
end
a = Threads.threadid()
means = zeros(10)
for cyc in 1:10
yield()
s = 0
for i in 1:Int(n/10)
s += rand()
end
means[cyc] = s/(n/10)
end
return (a, Threads.threadid(), time() - t0, n, means)
end
該程序的參數(shù) n 必須是 10 的倍數(shù)。它還有幾行代碼用來(lái)記錄它是在哪個(gè)線程上運(yùn)行的,以及完成時(shí)間。這個(gè)完成時(shí)間是從一個(gè)全局性的 t0 時(shí)刻開(kāi)始計(jì)算的。在這 10 組數(shù)據(jù)的每一組這個(gè)周期開(kāi)始之前,它都會(huì)先調(diào)用 yield(),使得調(diào)度器可以切換到線程上的另一個(gè) task 去,并且在線程遷移時(shí)也會(huì)將 task 轉(zhuǎn)移到另一個(gè)線程上。
舉個(gè)例子,如果我們運(yùn)行 darts(1000),我們會(huì)得到 10 個(gè)均值,每個(gè)均值都是 100 個(gè)隨機(jī)數(shù)的計(jì)算結(jié)果。根據(jù)中心極限定理(central limit theorem),這些平均值應(yīng)該符合正態(tài)分布(normal distribution),其平均值與 underlying (uniform)distribution 的平均值相同。
為了得到樣本并繪制其分布情況,我啟動(dòng)了 20 個(gè) task,每個(gè) task 都運(yùn)行了 n=107?的 darts() 程序。這樣就運(yùn)行了 200 個(gè)隨機(jī)試驗(yàn)(trial),每個(gè)試驗(yàn)(trial)中都選取了 100 萬(wàn)個(gè)隨機(jī)數(shù),然后計(jì)算并記錄其平均值。我們還需要對(duì)分布的平均數(shù)有一個(gè)高度準(zhǔn)確的估計(jì),所以我又啟動(dòng)了一個(gè) n=109?的任務(wù)來(lái)對(duì)此進(jìn)行計(jì)算。我們知道理論上的平均數(shù)應(yīng)該是 0.5,所以這個(gè)結(jié)果會(huì)告訴我們 rand() 的偏差有多大。通過(guò)一個(gè)簡(jiǎn)單的修改,該程序可以用于其他基礎(chǔ)分布(underlying distribution),不過(guò)那些分布的平均值我們可能就無(wú)法這么簡(jiǎn)單地分析得知了。
我用下面的方法啟動(dòng)了這些 tasks:
begin
t0 = time()
tsm = [@tspawnat rand(1:2) darts(n) for n in [repeat([1e7], 20); 1e9]]
end
每個(gè) task 都可以拿到 t0,所以他們都可以報(bào)告出他們完成耗時(shí)多少。最開(kāi)始調(diào)用的 rand(1:2) 會(huì)將每個(gè) task 以相等概率分配給第一個(gè)線程或第二個(gè)線程。我重復(fù)五次進(jìn)行了這個(gè)實(shí)驗(yàn),然后跑另一個(gè)實(shí)驗(yàn)也執(zhí)行了五次,另一個(gè)實(shí)驗(yàn)中除了使用了我修改過(guò)的 @tspawnat 宏來(lái)禁用線程遷移之外,其他沒(méi)有什么變化。
為了查看每個(gè)一個(gè)實(shí)驗(yàn)的分布情況,我們可以將樣本平均值收集到一個(gè)數(shù)組中,然后用 Plots 包中的 histogram()函數(shù)來(lái)繪制出來(lái)。Julia 繪圖系統(tǒng)有個(gè)概述文章介紹了如何使用 histogram() 以及本文中使用到的其他繪圖函數(shù)。結(jié)果顯示在下圖中,這個(gè)疊加上來(lái)的條形圖就是使用 109?數(shù)字計(jì)算的平均值。
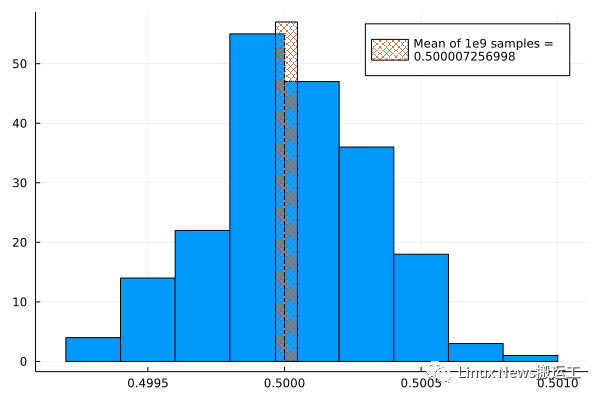
[隨機(jī)數(shù)分布]
該分布近似于正態(tài)分布,均值也正確。
實(shí)驗(yàn)包括了 20 個(gè)耗時(shí)較短的 task 以及一個(gè)需要 100 倍時(shí)間的 task。我樂(lè)觀地認(rèn)為這可以展示出線程遷移的效果,因?yàn)檎{(diào)度器就可以有機(jī)會(huì)把 task 從那個(gè)包含了長(zhǎng)期運(yùn)行的計(jì)算的線程上移走,這正是線程遷移功能所希望改善的情況。至于那些各個(gè) task 的計(jì)算資源需求很接近的計(jì)算場(chǎng)景則應(yīng)該不會(huì)從遷移中得到什么好處。
在五次實(shí)驗(yàn)中,啟用了線程遷移的 21 個(gè)任務(wù)的完成時(shí)間平均值為 0.71 秒,而禁用了遷移的測(cè)試中耗時(shí)平均值為 1.5 秒。仔細(xì)深入查看這些耗時(shí)數(shù)據(jù)就可以了解到線程遷移是如何使 job 完成的速度提高了一倍。下圖顯示了所有 10 個(gè)實(shí)驗(yàn)的完結(jié)時(shí)間(return time),并畫了一條線來(lái)幫助人們可以看出最快的那個(gè)實(shí)驗(yàn)的耗時(shí)數(shù)據(jù)。
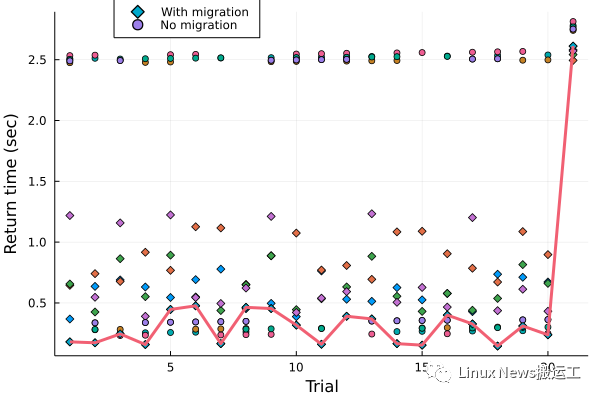
[任務(wù)遷移圖]
數(shù)據(jù)顯示,運(yùn)行 darts(1e7) 需要 0.024 秒,darts(1e9) 需要 2.4 秒,這個(gè)數(shù)據(jù)符合我們期望的運(yùn)行時(shí)間比例。編號(hào)為 21 的試驗(yàn)就是 darts(1e9) 的這個(gè)任務(wù),它在并行運(yùn)行時(shí)需要大約 2.5 秒。該圖清楚地表明,在沒(méi)有遷移的情況下大約有一半的 task 會(huì)被卡住,與那一個(gè)最繁重的 task 任務(wù)共用同一個(gè)線程。另一半任務(wù)則會(huì)很快完成,在此之后,這個(gè)線程就會(huì)無(wú)事可做,被浪費(fèi)了。對(duì)比情況下,線程遷移則會(huì)將 task 轉(zhuǎn)移到空閑線程上,從而得到更好的負(fù)載平衡,也就可以更快地完成整個(gè)工作。觀察 Threads.threadid() 調(diào)用的返回值,也證實(shí)了大約一半的任務(wù)會(huì)進(jìn)行遷移。
這個(gè)實(shí)驗(yàn)表明,新的線程遷移功能正在如預(yù)期的那樣起到了效果。在任務(wù)的運(yùn)行時(shí)間明顯不平衡,或者有一些任務(wù)被阻塞在等待 I/O 或其他 event 的情況下,線程遷移功能可以加快異步多線程計(jì)算的速度。
在本節(jié)和上一節(jié)這種類似的計(jì)算任務(wù)中,任務(wù)之間是完全獨(dú)立執(zhí)行的,不需要協(xié)調(diào)。如果一個(gè)程序中有些地方必須要等待所有異步任務(wù)完成后才能進(jìn)入下一階段,那這里就可以使用 @sync 宏了,就會(huì)一直等到在宏出現(xiàn)的范圍內(nèi)所產(chǎn)生的 task 都完成。
Conclusion
并發(fā)(concurrency),本質(zhì)上就是一件很困難的的事情。并發(fā)程序(concurrent program)更加難調(diào)試和理解。Julia 并沒(méi)有消除這些困難,也就是說(shuō)程序員仍然需要自己注意 race condition、一致性(consistency)和正確性(correctness)。但是 Julia 的宏以及那些用于 task 與數(shù)據(jù)并行處理的函數(shù)在許多情況下可以讓簡(jiǎn)單的事情變得更容易,而更復(fù)雜的問(wèn)題也可以變得可以實(shí)現(xiàn)出來(lái)了。
這個(gè)領(lǐng)域的開(kāi)發(fā)也非常活躍,從 Folds 等軟件包,到比如調(diào)度器操作的實(shí)現(xiàn)細(xì)節(jié)(這是近期實(shí)現(xiàn)的任務(wù)遷移功能的底層功臣)。我們可以期待 Julia 的并發(fā)計(jì)算的情況將會(huì)繼續(xù)提高。也同樣需要認(rèn)識(shí)到,并發(fā)生態(tài)系統(tǒng)的一些更好的功能仍然未能加入標(biāo)準(zhǔn)庫(kù)和官方文檔,想要利用好這些產(chǎn)品的優(yōu)勢(shì)的程序員都需要努力跟上這個(gè)不斷變化的世界。
全文完
LWN 文章遵循 CC BY-SA 4.0 許可協(xié)議。
長(zhǎng)按下面二維碼關(guān)注,關(guān)注 LWN 深度文章以及開(kāi)源社區(qū)的各種新近言論~
