男女操逼拍小视频,蜜桃av日韩网址,av影音先锋久久,欧美成人手机在线,丁香五月网页,天天射天天射av,国产精品久久久久久无码红治院 ,久久免费视频精品

算法的重要性，我就不多說(shuō)了吧，想去大廠，就必須要經(jīng)過(guò)基礎(chǔ)知識(shí)和業(yè)務(wù)邏輯面試+算法面試。所以，為了提高大家的算法能力，這個(gè)公眾號(hào)后續(xù)每天帶大家做一道算法題，題目就從LeetCode上面選！

今天和大家聊的問(wèn)題叫做?不同的二叉搜索樹 II，我們先來(lái)看題面：

https://leetcode-cn.com/problems/binary-tree-inorder-traversal/

Given an integer n, generate all structurally unique BST's (binary search trees) that store values 1 ... n.

題意

給定一個(gè)整數(shù) n，生成所有由 1 ... n 為節(jié)點(diǎn)所組成的二叉搜索樹。

樣例

解題

https://www.cnblogs.com/techflow/p/13594735.html

拿到手我們思路沒(méi)多少，但是發(fā)現(xiàn)的問(wèn)題卻一大堆。比如說(shuō)我們?cè)趺礃?gòu)建這些BST，并且怎么判斷兩顆BST是否重復(fù)呢？難道要整個(gè)遍歷一遍之后，一個(gè)節(jié)點(diǎn)一個(gè)節(jié)點(diǎn)地判斷是否相同嗎？顯然這也太耗時(shí)了，而且編碼也不容易。舉個(gè)例子[2, 1, 3]和[2, 3, 1]生成的BST是一樣的，這種情況很難解決。

即使我們解決了這個(gè)問(wèn)題，那么又怎么樣保證我們可以順利找到所有的答案，而不會(huì)有所遺漏呢？這兩個(gè)核心的問(wèn)題很難回答，并且你會(huì)發(fā)現(xiàn)越想越復(fù)雜。

這個(gè)有點(diǎn)像什么呢？就好像是古代行軍打仗，攻打一個(gè)異常堅(jiān)固的堡壘，正面攻堅(jiān)可能非常困難，我們想出來(lái)的辦法都在敵人的預(yù)料之中，總能找到破解之道。這個(gè)時(shí)候就需要我們有敏銳的意識(shí)，就好像是一個(gè)經(jīng)驗(yàn)豐富的老將，觀察地形之后發(fā)現(xiàn)強(qiáng)攻不可為，那么自然就會(huì)退下來(lái)想一想其他的辦法。

我們做題也是一樣，正面硬剛做不出來(lái)，再耗下去也不會(huì)有好辦法，往往就需要出奇制勝了。

我們?cè)囍褑?wèn)題縮小，化整為零，如果n=1，那么很簡(jiǎn)單，BST就只有一種，這個(gè)是我們都知道的東西。如果n=2呢，也不難，只有兩種，無(wú)非是[1, 2]和[2, 1]。這時(shí)候我們停住，來(lái)思考一個(gè)問(wèn)題，n=2的情況和n=1的情況有什么區(qū)別呢？

如果仔細(xì)想，會(huì)發(fā)現(xiàn)其實(shí)沒(méi)什么區(qū)別，我們只不過(guò)是在n=1的情況當(dāng)中加入了2這個(gè)數(shù)字而已。同理，我們發(fā)散一下n=k和n=k+1的時(shí)候生成的BST之間有什么關(guān)系呢？如果我們知道了n=k時(shí)候的所有BST，可不可以利用這個(gè)關(guān)系生成n=k+1時(shí)的所有結(jié)果呢？

當(dāng)然是可以的，實(shí)際上這也是一個(gè)很好的做法。這是一種最基本的二叉樹，假設(shè)我們要往其中插入一個(gè)最大的節(jié)點(diǎn)，我們很容易發(fā)現(xiàn)，一共有三種方法。

第一種方法將原搜索樹作為新節(jié)點(diǎn)的左孩子節(jié)點(diǎn)。

第二種方法是將新的節(jié)點(diǎn)插入根節(jié)點(diǎn)的右側(cè)，代替根節(jié)點(diǎn)的右孩子。由于這個(gè)新加入的節(jié)點(diǎn)大于其他所有節(jié)點(diǎn)，所以根節(jié)點(diǎn)的右孩子會(huì)變成它的左孩子。

最后一種方法就是將它變成葉子節(jié)點(diǎn)，也就是放在最底層。

我們稍加思考就可以想明白，如果要把一個(gè)最大的元素插入BST，那么它只能夠放在最右側(cè)的樹分支上。也就是說(shuō)當(dāng)我們從n=k的情況推導(dǎo)k+1時(shí)，根據(jù)最右側(cè)鏈路長(zhǎng)度的不同，會(huì)衍生出多個(gè)解來(lái)。只要抓住了這一點(diǎn)，這其中的遞推關(guān)系就很明顯了。

我們用代碼來(lái)實(shí)現(xiàn)這個(gè)想法，思路雖然簡(jiǎn)單，但是實(shí)現(xiàn)起來(lái)要復(fù)雜一些，有很多細(xì)節(jié)需要考慮。我在這里不一一列舉了，大家查看代碼當(dāng)中的注釋吧。

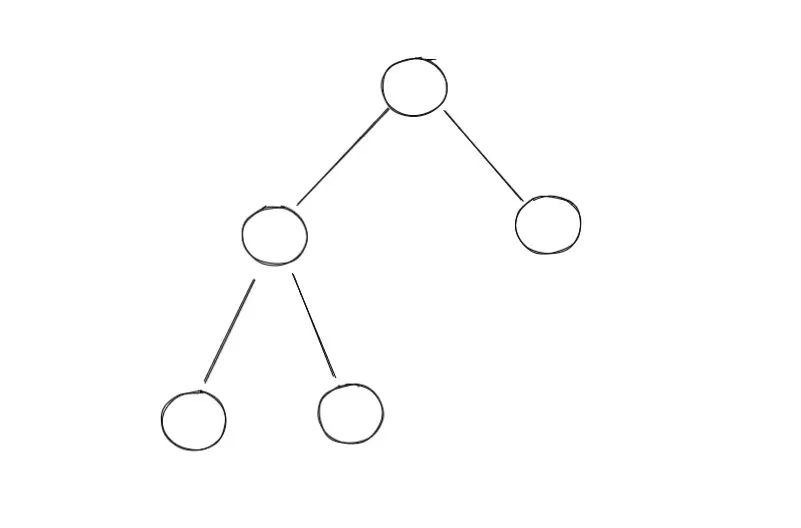
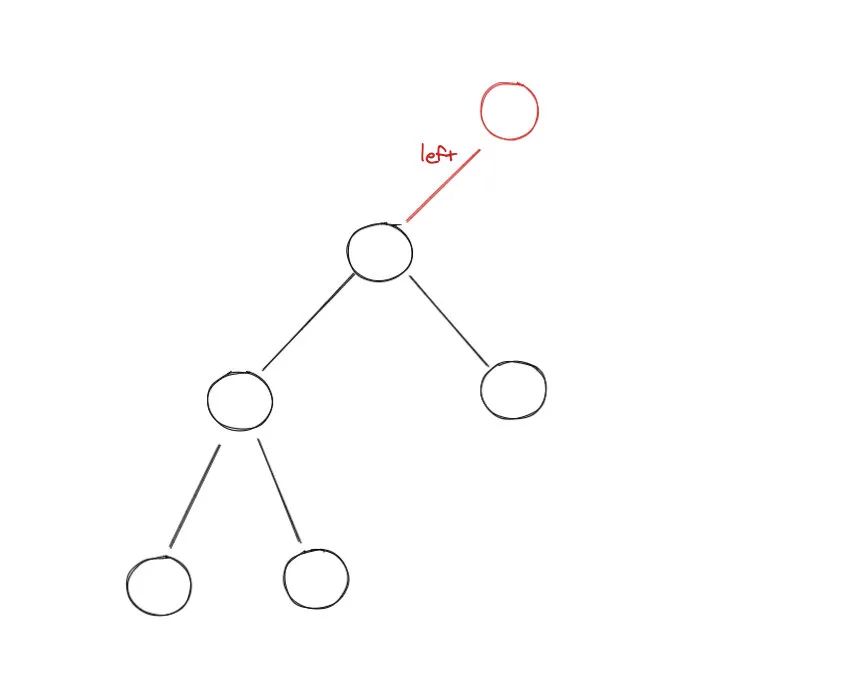
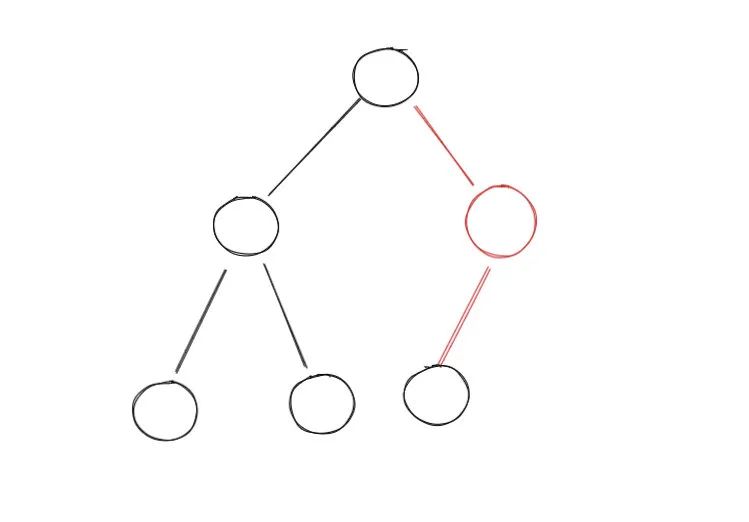
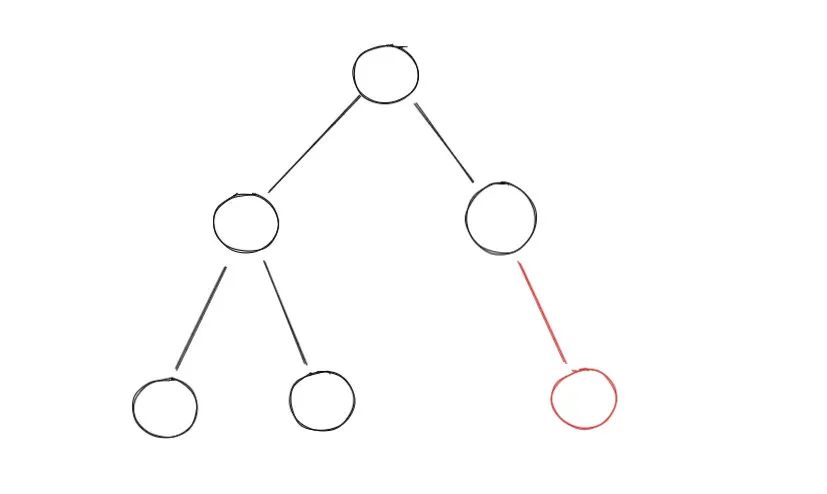
class Solution:
????def generateTrees(self, n: int) -> List[TreeNode]:
????????ret?= []
????????
????????# 拷貝二叉樹
????????def copyTree(node):
????????????if?node is?None:
????????????????return?None
????????????u?= TreeNode(node.val)
????????????u.left?= copyTree(node.left)
????????????u.right?= copyTree(node.right)
????????????return?u
????????
????????def dfs(n):
????????????# n=1只有一種情況
????????????if?n == 1:
????????????????ret.append(TreeNode(1)) 
????????????????return
????????????
????????????dfs(n-1)
????????????# 遍歷n=k時(shí)的所有情況
????????????for?i in range(len(ret)):
????????????????u?= ret[i]
????????????????node = TreeNode(n)
????????????????node.left?= u
????????????????ret[i] = node
????????????????
????????????????it = u
????????????????rank = 0
????????????????# 將n插入最右側(cè)鏈路當(dāng)中，有幾種可以選擇的位置，就會(huì)誕生幾種新的放法
????????????????while?it is?not None:
????????????????????node = TreeNode(n)
????????????????????# 為了防止答案之間互不影響，所以需要把樹拷貝一份
????????????????????new?= copyTree(u)
????????????????????cur = new
????????????????????
????????????????????# rank記錄的是每一個(gè)解對(duì)應(yīng)的n放入的深度
????????????????????for?_ in range(rank):
????????????????????????cur = cur.right
????????????????????
????????????????????node.left?= cur.right
????????????????????cur.right?= node
????????????????????
????????????????????ret.append(new)
????????????????????
????????????????????it = it.right
????????????????????rank += 1
????????????
????????if?n == 0:
????????????return?ret
????????dfs(n)
????????return?ret

這種方法當(dāng)然是可行的，我們也成功做了出來(lái)。但是它也有很多問(wèn)題，最大的問(wèn)題就是細(xì)節(jié)太多，而且處理起來(lái)太麻煩了。那么有沒(méi)有簡(jiǎn)單一點(diǎn)的方法呢？

我們來(lái)思考一個(gè)問(wèn)題，我們通過(guò)遞推和迭代從n=k構(gòu)造出了n=k+1的情況，這一種構(gòu)造和遞推的思路非常巧妙。但問(wèn)題是，我們構(gòu)造和遞推的方法難道只有這一種嗎？能不能想出其他簡(jiǎn)便一些的構(gòu)造和遞推的方法呢？

既然我這么說(shuō)，那么很顯然，它是可以的，怎么做呢？

這要用到BST另外一個(gè)性質(zhì)，我們都知道對(duì)于BST來(lái)說(shuō)，它有一個(gè)性質(zhì)是對(duì)于根節(jié)點(diǎn)來(lái)說(shuō)，所有比它小的元素都出現(xiàn)在它的左側(cè)，比它大的元素都在它的右側(cè)。那么假如我們知道根節(jié)點(diǎn)是i，那么我們可以確定1到i-1出現(xiàn)在它的左子樹，i+1到n出現(xiàn)在它的右子樹。假設(shè)說(shuō)我們已經(jīng)得到了左右子樹的所有情況，我們只需要把它們兩兩組合在一起，是不是就得到了答案了呢？

我這么說(shuō)你們理解起來(lái)可能還是會(huì)覺(jué)得有些費(fèi)勁，但是一旦查看代碼，你們一定會(huì)為這段邏輯的簡(jiǎn)易性而折服，看起來(lái)實(shí)在是太簡(jiǎn)明也太巧妙了。

class?Solution:
????def?generateTrees(self, n: int)?-> List[TreeNode]:
????????ret = []
????????
????????def?dfs(l, r):
????????????cur = []
????????????if?r < l:
????????????????cur.append(None)
????????????????return?cur
????????????
????????????# 枚舉作為樹根的元素
????????????for?i in?range(l, r+1):
????????????????# 枚舉左右子樹的所有子樹的構(gòu)成情況
????????????????for?u in?dfs(l, i-1):
????????????????????for?v in?dfs(i+1, r):
????????????????????????node = TreeNode(i)
????????????????????????node.left = u
????????????????????????node.right = v
????????????????????????cur.append(node)
????????????return?cur 
????????????
????????if?n == 0:
????????????return?ret
????????return?dfs(1, n)