數(shù)據(jù)科學中必須知道的5個關于奇異值分解（SVD）的應用

點擊上方“小白學視覺”，選擇加"星標"或“置頂”

重磅干貨，第一時間送達

概覽

• 奇異值分解(SVD)是數(shù)據(jù)科學中常見的降維技術

• 我們將在這里討論5個必須知道的SVD應用，并了解它們在數(shù)據(jù)科學中的作用

• 我們還將看到在Python中實現(xiàn)SVD的三種不同方法

介紹

“Another day has passed, and I still haven’t used y = mx + b.”

這聽起來是不是很熟悉？我經常聽到我大學的熟人抱怨他們花了很多時間的代數(shù)方程在現(xiàn)實世界中基本沒用。

好吧,但我可以向你保證，并不是這樣的。特別是如果你想開啟數(shù)據(jù)科學的職業(yè)生涯。

線性代數(shù)彌合了理論與概念實際實施之間的差距。對線性代數(shù)的掌握理解打開了我們認為無法理解的機器學習算法的大門。線性代數(shù)的一種這樣的用途是奇異值分解(SVD)用于降維。

你在數(shù)據(jù)科學中一定很多次遇到SVD。它無處不在，特別是當我們處理降維時。但它是什么？它是如何工作的？SVD應用有什么？

事實上，SVD是推薦系統(tǒng)的基礎，而推薦系統(tǒng)是谷歌，YouTube，亞馬遜，F(xiàn)acebook等大公司的核心。

我們將在本文中介紹SVD的五個超級有用的應用，并將探討如何在Python中以三種不同的方式使用SVD。

奇異值分解(SVD)的應用

我們將在此處遵循自上而下的方法并首先討論SVD應用。如果你對它如何工作感興趣的，我在下面會講解SVD背后的數(shù)學原理。現(xiàn)在你只需要知道四點來理解這些應用：

• SVD是將矩陣A分解為3個矩陣--U，S和V。

• S是奇異值的對角矩陣。將奇異值視為矩陣中不同特征的重要性值

• 矩陣的秩是對存儲在矩陣中的獨特信息的度量。秩越高，信息越多

• 矩陣的特征向量是數(shù)據(jù)的最大擴展或方差的方向

在大多數(shù)應用中，我們希望將高秩矩陣縮減為低秩矩陣，同時保留重要信息。

1. SVD用于圖像壓縮

我們有多少次遇到過這個問題？我們喜歡用我們的智能手機瀏覽圖像，并隨機將照片保存。然后突然有一天 ，提示手機沒有空間了！而圖像壓縮有助于解決這一問題。

它將圖像的大小(以字節(jié)為單位)最小化到可接受的質量水平。這意味著你可以在相同磁盤空間中存儲更多圖像。

圖片壓縮利用了在SVD之后僅獲得的一些奇異值很大的原理。你可以根據(jù)前幾個奇異值修剪三個矩陣，并獲得原始圖像的壓縮近似值，人眼無法區(qū)分一些壓縮圖像。以下是在Python中編寫的代碼：

# 下載圖片 "https://cdn.pixabay.com/photo/2017/03/27/16/50/beach-2179624_960_720.jpg"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import cv2

# 灰度化讀取圖片
img = cv2.imread('beach-2179624_960_720.jpg', 0)

# 得到svd
U, S, V = np.linalg.svd(img)

# 得到矩陣的形狀
print(U.shape, S.shape, V.shape)

# 以不同component數(shù)繪制圖像
comps = [638, 500, 400, 300, 200, 100]

plt.figure(figsize = (16, 8))
for i in range(6):
  low_rank = U[:, :comps[i]] @ np.diag(S[:comps[i]]) @ V[:comps[i], :]
  if(i  == 0):
     plt.subplot(2, 3, i+1), plt.imshow(low_rank, cmap = 'gray'), plt.axis('off'), plt.title("Original Image with n_components =" + str(comps[i]))
  else:
     plt.subplot(2, 3, i+1), plt.imshow(low_rank, cmap = 'gray'), plt.axis('off'), plt.title("n_components =" + str(comps[i]))

Output:

如果你說即使是最后一張圖像，看起來好像也不錯！是的，如果沒有前面的圖像對比，我也不會猜到這是經過壓縮的圖像。

2. SVD用于圖像恢復

我們將通過矩陣填充的概念(以及一個很酷的Netflix示例)來理解圖像恢復。

矩陣填充是在部分觀察的矩陣中填充缺失元素的過程。Netflix問題就是一個常見的例子。

給定一個評級矩陣，其中每個元素(i，j)表示客戶i對電影j的評級，即客戶i觀看了電影j，否則該值為缺失值，我們想要預測剩余的元素以便對客戶于提出好的建議。

有助于解決這個問題的基本事實是，大多數(shù)用戶在他們觀看的電影和他們給這些電影的評級中都有一個模式。因此，評級矩陣幾乎沒有獨特的信息。這意味著低秩矩陣能夠為矩陣提供足夠好的近似。

這就是我們在SVD的幫助下所能夠實現(xiàn)的。

你還在哪里看到這樣的屬性？是的，在圖像矩陣中！由于圖像是連續(xù)的，大多數(shù)像素的值取決于它們周圍的像素。因此，低秩矩陣可以是這些圖像的良好近似。

下面是結果的一張截圖：

問題的整個表述可能很復雜并且需要了解其他一些概念。你可以參閱下面的論文^[1]。

3. SVD用于特征臉

論文“Eigenfaces for Recognition”于1991年發(fā)表。在此之前，大多數(shù)面部識別方法都涉及識別個體特征，如眼睛或鼻子，并根據(jù)這些特征之間的位置，大小和關系來開發(fā)模型。

特征臉方法試圖在面部圖像中提取相關信息，盡可能有效地對其進行編碼，并將一個面部編碼與數(shù)據(jù)庫中的模型編碼進行比較。

通過將每個面部表達為新面部空間中所選擇的特征臉的線性組合來獲得編碼。

讓我把這個方法分解為五個步驟：

• 收集面部訓練集

• 通過找到最大方差的方向-特征向量或特征臉來找到最重要的特征

• 選擇對應于最高特征值的M個特征臉。這些特征臉現(xiàn)在定義了一個新的面部空間

• 將所有數(shù)據(jù)投影到此面部空間中

• 對于新面部，將其投影到新面部空間中，找到空間中最近的面部，并將面部分類為已知或未知面部

你可以使用PCA和SVD找到這些特征臉。這是我在Labeled Faces in the Wild數(shù)據(jù)集中上執(zhí)行SVD后獲得的幾個特征臉中的第一個：

我們可以看到，只有前幾行中的圖像看起來像實際的面部。其他看起來很糟糕，因此我放棄了它們。我保留了總共120個特征臉，并將數(shù)據(jù)轉換為新的面部空間。然后我使用k近鄰分類器來預測基于面部的姓名。

你可以在下面看到分類報告。顯然，還有改進的余地。你可以嘗試調整特征臉的數(shù)量或使用不同的分類器進行試驗：

看看一些預測值及其真實標簽：

聚類是將類似對象劃分在一起的任務。這是一種無監(jiān)督的機器學習技術。對于我們大多數(shù)人來說，聚類是K-Means聚類(一種簡單但功能強大的算法)的代名詞,但是，這并不是準確的說法。

考慮以下情況：

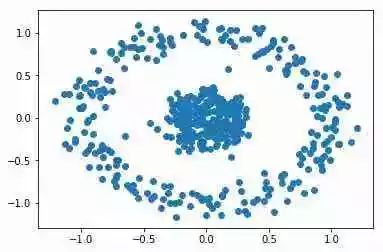
顯然，同心圓中有2個簇。但是，n_clusters = 2的KMeans給出了以下簇：

K-Means絕對不是這里使用的合適算法。譜聚類是一種可以解決這個問題的技術，它源于圖論。以下是基本步驟：

• 從數(shù)據(jù)Affnity matrix(A)或Adjacent matrix開始。這表示一個對象與另一個對象的相似程度。在圖中，這將表示點之間是否存在邊緣

• 找到每個對象的 Degree matrix (D) 。這是一個對角矩陣，其元素(i，i)等于對象i相似的對象數(shù)

• 找到Affnity matrix的 Laplacian matrix(L) (L)：L = A  -  D

• 根據(jù)它們的特征值找到Laplacian matrix的最高k個特征向量

• 在這些特征向量上運行k-means，將對象聚類為k類

你可以通過下面的鏈接閱讀完整的算法及其數(shù)學原理^2,而scikit-learn中譜聚類的實現(xiàn)類似于KMeans：

from sklearn.datasets import make_circles
from sklearn.neighbors import kneighbors_graph
from sklearn.cluster import SpectralClustering
import numpy as np
import matplotlib.pyplot as plt

# s生成數(shù)據(jù)
X, labels = make_circles(n_samples=500, noise=0.1, factor=.2)

# 可視化數(shù)據(jù)
plt.scatter(X[:, 0], X[:, 1])
plt.show()

# 訓練和預測
s_cluster = SpectralClustering(n_clusters = 2, eigen_solver='arpack',
        affinity="nearest_neighbors").fit_predict(X)

# 可視化結果
plt.scatter(X[:, 0], X[:, 1], c = s_cluster)
plt.show()

你將從上面的代碼中得到以下不錯的聚類結果：

5. SVD用于從視頻中刪除背景

想一想如何區(qū)分視頻背景和前景。視頻的背景基本上是靜態(tài)的 - 它看不到很多變化。所有的變化都在前景中看到。這是我們用來將背景與前景分開的屬性。

以下是我們可以采用的步驟來實現(xiàn)此方法：

• 從視頻創(chuàng)建矩陣M -- 這是通過定期從視頻中采樣圖像快照，將這些圖像矩陣展平為數(shù)組，并將它們存儲為矩陣M的列。

• 我們得到以下矩陣M的圖：

你認為這些水平和波浪線代表什么？花一點時間考慮一下。

水平線表示在整個視頻中不改變的像素值。基本上，這些代表了視頻中的背景。波浪線顯示變化并代表前景。

• 因此，我們可以將M視為兩個矩陣的總和 - 一個表示背景，另一個表示前景

• 背景矩陣沒有看到像素的變化，因此是多余的，即它沒有很多獨特的信息。所以，它是一個低秩矩陣

• 因此，M的低秩近似是背景矩陣。我們在此步驟中使用SVD

• 我們可以通過簡單地從矩陣M中減去背景矩陣來獲得前景矩陣

這是視頻一個刪除背景后的幀：

到目前為止，我們已經討論了SVD的五個非常有用的應用。但是，SVD背后的數(shù)學實際上是如何運作的？作為數(shù)據(jù)科學家，它對我們有多大用處？讓我們在下一節(jié)中理解這些要點。

SVD是什么？

我在本文中大量使用了“秩”這個術語。事實上，通過關于SVD及其應用的所有文獻，你將非常頻繁地遇到術語“矩陣的秩”。那么讓我們從了解這是什么開始。

矩陣的秩

矩陣的秩是矩陣中線性無關的行(或列)向量的最大數(shù)量。如果向量r不能表示為r1和r2的線性組合，則稱向量r與向量r1和r2線性無關。

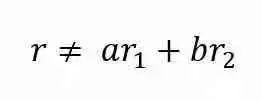
考慮下面的三個矩陣：

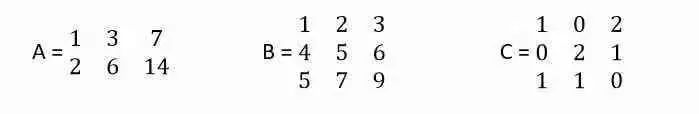
• 在矩陣A中，行向量r2是r1的倍數(shù)，r2 = 2 r1，因此它只有一個無關的行向量。Rank(A)= 1

• 在矩陣B中，行向量r3是r1和r2之和，r3 = r1 + r2，但r1和r2是無關的，Rank(B)= 2

• 在矩陣C中，所有3行彼此無關。Rank(C)= 3

矩陣的秩可以被認為是由矩陣表示的獨特信息量多少的代表。秩越高，信息越高。

SVD

SVD將矩陣分解為3個矩陣的乘積，如下所示：

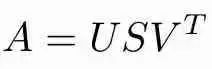
如果A是m x n矩陣：

• U是左奇異向量的m×m矩陣

• S是以遞減順序排列的奇異值的m×n對角矩陣

• V是右奇異向量的n×n矩陣

為什么SVD用于降維？

你可能想知道我們?yōu)槭裁匆洑v這種看似辛苦的分解。可以通過分解的替代表示來理解原因。見下圖：

分解允許我們將原始矩陣表示為低秩矩陣的線性組合。

在實際應用中，你將觀察到的只有前幾個(比如k)奇異值很大。其余的奇異值接近于零。因此，可以忽略除前幾個之外而不會丟失大量信息。請參見下圖中的矩陣截斷方式：

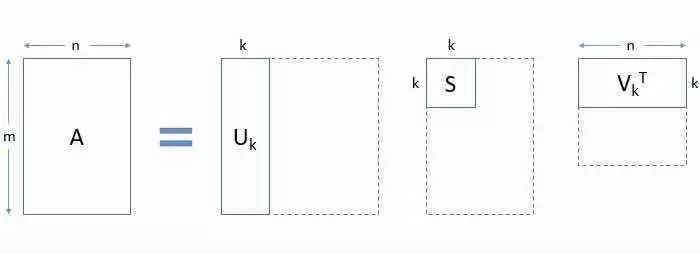
總結以下3點：

• 使用SVD，我們能夠用3個較小的矩陣U，S和V表示我們的大矩陣A

• 這在大型計算中很有用

• 我們可以得到A的k-秩近似。為此，選擇前k個奇異值并相應地截斷3個矩陣。

3種在Python中使用SVD的方法

我們知道什么是SVD，它是如何工作的，以及它在現(xiàn)實世界中的用途。但是我們如何自己實現(xiàn)SVD呢？

SVD的概念聽起來很復雜。你可能想知道如何找到3個矩陣U，S和V。如果我們手動計算這些矩陣，這是一個漫長的過程。

幸運的是，我們不需要手動執(zhí)行這些計算。我們可以用三種簡單的方式在Python中實現(xiàn)SVD。

1. numpy中的SVD

NumPy是Python中科學計算的基礎包。它具有有用的線性代數(shù)功能以及其他應用。

你可以使用numpy.linalg中的SVD獲取完整的矩陣U，S和V。注意，S是對角矩陣，這意味著它的大多數(shù)元素都是0。這稱為稀疏矩陣。為了節(jié)省空間，S作為奇異值的一維數(shù)組而不是完整的二維矩陣返回。

import numpy as np
from numpy.linalg import svd
# 定義二維矩陣
A = np.array([[4, 0], [3, -5]])
U, S, VT = svd(A)
print("Left Singular Vectors:")
print(U)
print("Singular Values:") 
print(np.diag(S))
print("Right Singular Vectors:") 
print(VT)
# 檢查分解是否正確
# @ 表示矩陣乘法
print(U @ np.diag(S) @ VT)

2. scikit-learn中的Truncated SVD

在大多數(shù)常見的應用中，我們不希望找到完整的矩陣U，S和V。我們在降維和潛在語義分析中看到了這一點，還記得嗎？

我們最終會修剪矩陣，所以為什么要首先找到完整的矩陣？

在這種情況下，最好使用sklearn.decomposition中的TruncatedSVD。你可以通過n_components參數(shù)指定所需的特征數(shù)量輸出。n_components應嚴格小于輸入矩陣中的特征數(shù)：

import numpy as np
from sklearn.decomposition import TruncatedSVD
A = np.array([[-1, 2, 0], [2, 0, -2], [0, -2, 1]])
print("Original Matrix:")
print(A)
svd =  TruncatedSVD(n_components = 2)
A_transf = svd.fit_transform(A)
print("Singular values:")
print(svd.singular_values_)
print("Transformed Matrix after reducing to 2 features:")
print(A_transf)

3. scikit-learn中的Randomized SVD

Randomized SVD提供與Truncated SVD相同的結果，并且具有更快的計算時間。Truncated SVD使用ARPACK精確求解，但隨機SVD使用了近似技術。

import numpy as np
from sklearn.utils.extmath import randomized_svd

A = np.array([[-1, 2, 0], [2, 0, -2], [0, -2, 1]])
u, s, vt = randomized_svd(A, n_components = 2)

print("Left Singular Vectors:")
print(u)

print("Singular Values:") 
print(np.diag(s))

print("Right Singular Vectors:") 
print(vt)

^[1]: https://sci-hub.tw/10.1145/3274250.3274261