Go 數(shù)據(jù)結(jié)構(gòu)和算法篇（八）：快速排序

一、實(shí)現(xiàn)原理

歸并排序算法雖好，但是不是原地排序算法，需要消耗額外的內(nèi)存空間，今天我們要介紹的是常規(guī)排序里綜合排名最高的排序算法：快速排序，江湖人稱「快排」。

快排的核心思想是這樣的：

如果要排序數(shù)據(jù)序列中下標(biāo)從 p 到 r 之間的一組數(shù)據(jù)，我們選擇 p 到 r 之間的任意一個(gè)數(shù)據(jù)作為 pivot（分區(qū)點(diǎn)），假設(shè)對應(yīng)下標(biāo)是 q。

遍歷 p 到 r 之間的數(shù)據(jù)，將小于 pivot 的放到左邊，將大于 pivot 的放到右邊，將 pivot 放到中間。經(jīng)過這一步驟之后，數(shù)據(jù)序列 p 到 r 之間的數(shù)據(jù)就被分成了三個(gè)部分，前面 p 到 q-1 之間都是小于 pivot 的，中間是 pivot，后面的 q+1 到 r 之間是大于 pivot 的。

圖示如下：

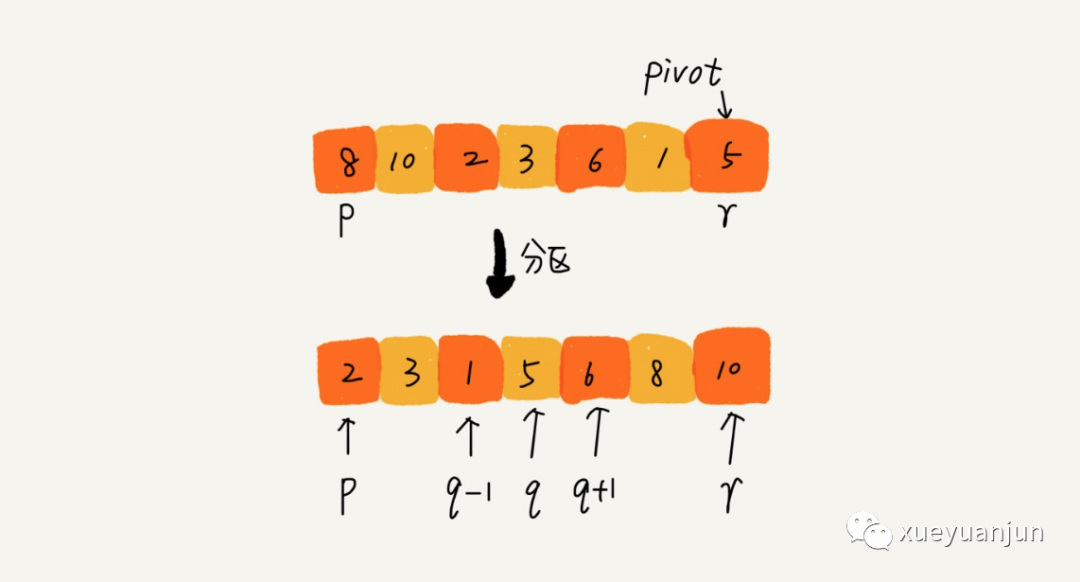
根據(jù)分治、遞歸的處理思想，我們可以用遞歸排序下標(biāo)從 p 到 q-1 之間的數(shù)據(jù)和下標(biāo)從 q+1 到 r 之間的數(shù)據(jù)，直到區(qū)間縮小為 1，就說明所有的數(shù)據(jù)都有序了，而且你可以看到我們不需要像歸并排序那樣做合并操作，也就不需要額外的內(nèi)存空間，在時(shí)間復(fù)雜度和歸并排序一樣的情況下，有著更好的空間復(fù)雜度表現(xiàn)。

快速排序首先要找到分區(qū)點(diǎn) pivot，一般我們會將數(shù)據(jù)序列最后一個(gè)元素或者第一個(gè)元素作為 pivot。假設(shè)我們以最后一個(gè)元素作為分區(qū)點(diǎn)，然后通過兩個(gè)變量 i 和 j 作為下標(biāo)來遍歷數(shù)據(jù)序列，當(dāng)下標(biāo) j 對應(yīng)數(shù)據(jù)小于 pivot 時(shí)，交換 i 和 j 對應(yīng)的數(shù)據(jù)，并且將 i 的指針往后移動一位，否則 i 不動。下標(biāo) j 是始終往后移動的，j 到達(dá)終點(diǎn)后，將 pivot 與下標(biāo) i 對應(yīng)數(shù)據(jù)交換，這樣最終將 pivot 置于數(shù)據(jù)序列中間，[0...i-1] 區(qū)間的數(shù)據(jù)都比 pivot 小，[i+1...j] 之間的數(shù)據(jù)都比 pivot 大，我們以遞歸的方式處理該流程，最終整個(gè)數(shù)據(jù)序列都會變成有序的，對應(yīng)的算法操作流程如下：

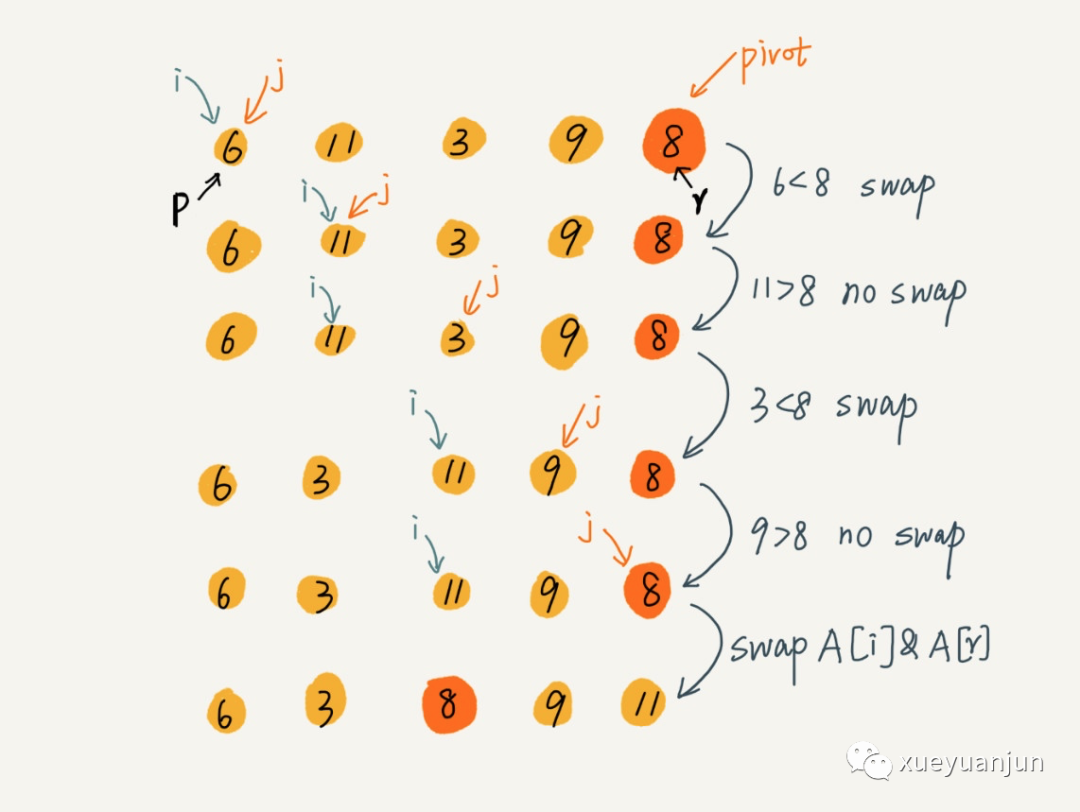
二、示例代碼

將上述流程轉(zhuǎn)化為 Go 代碼實(shí)現(xiàn)如下：

package main

import "fmt"

// 快速排序入口函數(shù)
func quickSort(nums []int, p int, r int) {
    // 遞歸終止條件
    if p >= r {
        return
    }
    // 獲取分區(qū)位置
    q := partition(nums, p, r)
    // 遞歸分區(qū)（排序是在定位 pivot 的過程中實(shí)現(xiàn)的）
    quickSort(nums, p, q - 1)
    quickSort(nums, q + 1, r)
}

// 定位 pivot
func partition(nums []int, p int, r int) int {
    // 以當(dāng)前數(shù)據(jù)序列最后一個(gè)元素作為初始 pivot
    pivot := nums[r]
    // 初始化 i、j 下標(biāo)
    i := p
    // 后移 j 下標(biāo)的遍歷過程
    for j := p; j < r; j++ {
        // 將比 pivot 小的數(shù)丟到 [p...i-1] 中，剩下的 [i...j] 區(qū)間都是比 pivot 大的
        if nums[j] < pivot {
            // 互換 i、j 下標(biāo)對應(yīng)數(shù)據(jù)
            nums[i], nums[j] = nums[j], nums[i]
            // 將 i 下標(biāo)后移一位
            i++
        }
    }

    // 最后將 pivot 與 i 下標(biāo)對應(yīng)數(shù)據(jù)值互換
    // 這樣一來，pivot 就位于當(dāng)前數(shù)據(jù)序列中間，i 也就是 pivot 值對應(yīng)的下標(biāo)
    nums[i], nums[r] = pivot, nums[i]
    // 返回 i 作為 pivot 分區(qū)位置
    return i
}

func main() {
    nums := []int{4, 5, 6, 7, 8, 3, 2, 1}
    quickSort(nums, 0, len(nums) - 1)
    fmt.Println(nums)
}

運(yùn)行上述代碼，打印結(jié)果如下，表明快速排序成功：

三、性能分析

正如我們前面所說的，快速排序是原地排序算法，時(shí)間復(fù)雜度和歸并排序一樣，也是 O(nlogn)，這個(gè)時(shí)間復(fù)雜度數(shù)據(jù)量越大，越優(yōu)于 O(n²)。

但是快速排序也有其缺點(diǎn)，因?yàn)樯婕暗綌?shù)據(jù)的交換，有可能破壞原來相等元素的位置排序，所以是不穩(wěn)定的排序算法。

盡管如此，憑借其良好的時(shí)間復(fù)雜度表現(xiàn)和空間復(fù)雜度的優(yōu)勢，快速排序在工程實(shí)踐中應(yīng)用較多。

關(guān)于線性表結(jié)構(gòu)的排序算法我們就簡單介紹到這里，下篇教程，我們來給大家介紹著名的線性表結(jié)構(gòu)查找算法 —— 二分查找。