面試超級愛問的全排列！！！

我準(zhǔn)備了 1000 本電子書和計(jì)算機(jī)各領(lǐng)域高清思維導(dǎo)圖 100 張，關(guān)注后回復(fù)【資源】，即可獲取！更可回復(fù)【內(nèi)推】加入 BAT 內(nèi)推群！

今天為大家分享如何用算法來求全排列！話不多說，直接看題！

01、全排列概念

什么是全排列？從 n 個(gè)不同元素中任取 m（m≤n）個(gè)元素，按照一定的順序排列起來，叫做從 n 個(gè)不同元素中取出 m 個(gè)元素的一個(gè)排列。當(dāng) m=n 時(shí)所有的排列情況叫全排列。

比如 [1,2,3] 全排列共有 6 種：

02、全排列題目

然后把上面的全排列稍微改改，就變成了一道算法題。。。

示例:

輸入: [1,2,3]

輸出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

03、題解分析

這種由基礎(chǔ)數(shù)學(xué)知識改編而成的題目，在面試時(shí)還是很受歡迎的。因?yàn)樽鳛槊嬖嚬伲梢杂眠@種題目，來顯示自己的博學(xué)。（謬論）

假如我們不是做算法題，而是做數(shù)學(xué)題。我們會一個(gè)位置一個(gè)位置的來考慮，先寫出以1開頭的排列，再寫出以2開頭的排列，最后寫出以3開頭的排列。

這種思路是不是很像深度優(yōu)先（DFS）的求解過程呢？

1、我們先選擇 1，然后為 1 的第二位選擇 2，此時(shí) 1 的 第三位只能選擇 3。

2、然后完成了上面的步驟，我們需要回退到 1，因?yàn)橹挥?1 這里還存在別的選擇 1-3，然后填寫 1-3 后，只有 1-3-2 一種選擇。

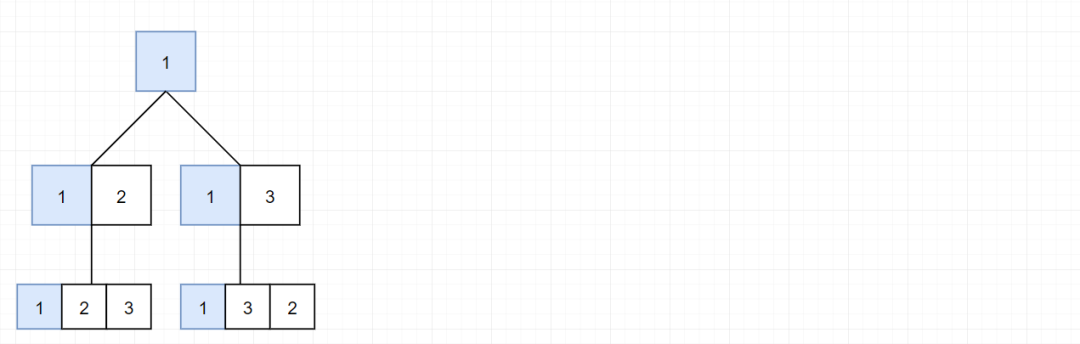
3、此時(shí)我們需要從 1-3-2，回退到 1-3，再回退到 1，再回退到 根節(jié)點(diǎn)，然后重新選擇 2。

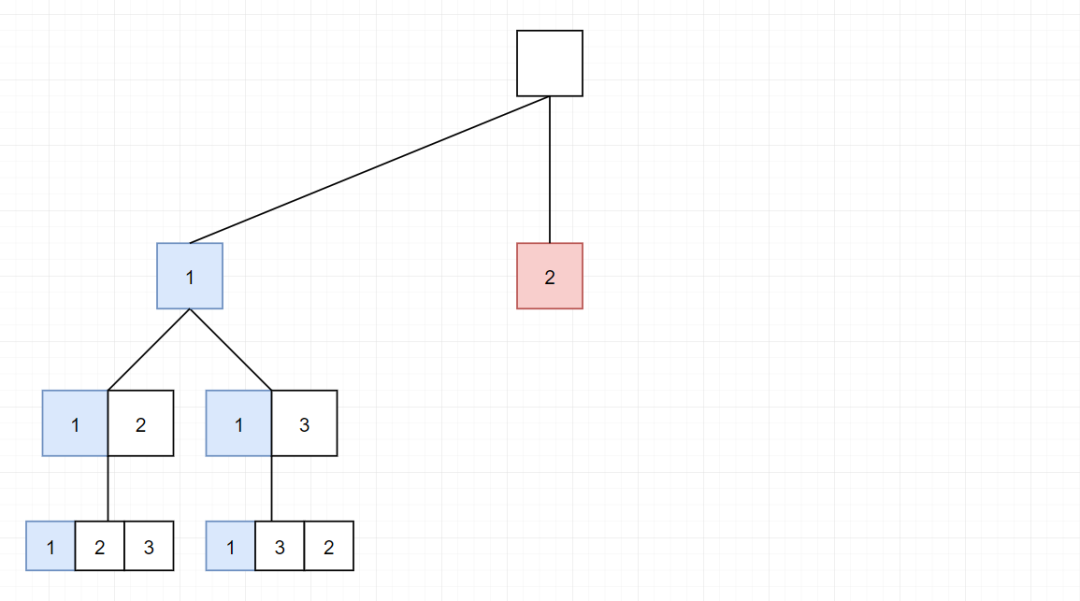
4、后面的流程與前面相似，我就不一步步的描述了。

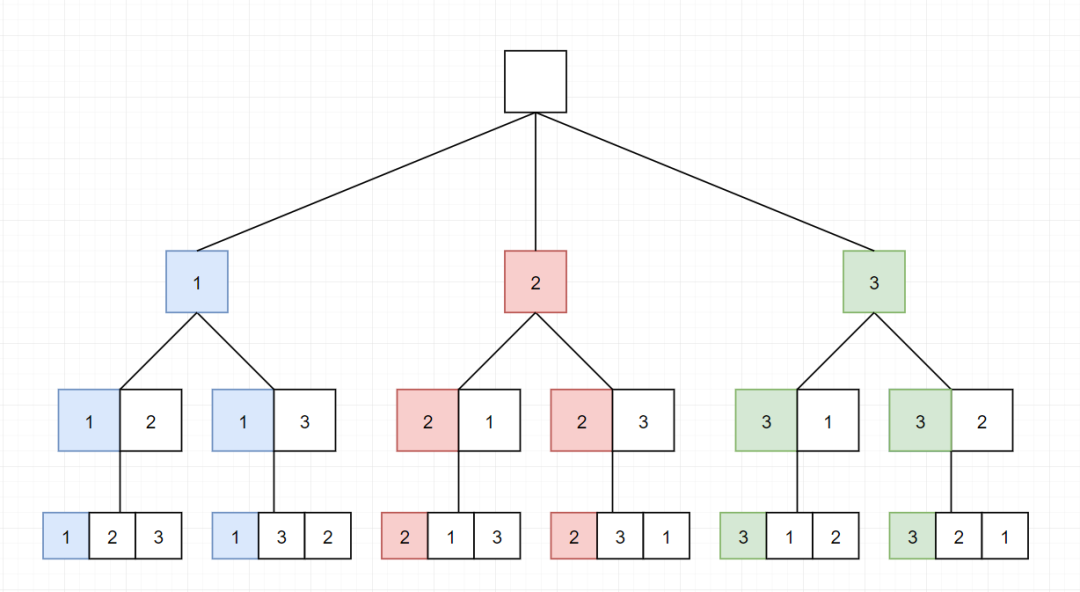
當(dāng)然，如果不省略其回溯過程，就是下面這個(gè)樣子：

上面分析是分析完了，但是仍然不妨礙你繼續(xù)懵逼。。。“題目中不是給我的是一個(gè)數(shù)組嗎？作為一個(gè)合格的算法小白，我特么根本就不知道 DFS 在這里面咋用啊！！”本來想扔完代碼就走，想了想還是決定講一下。

我們把代碼先丟出來（注意，這個(gè)代碼不是最優(yōu)的，這樣寫只是易于大家理解。比如我們還可以通過置換的方式來進(jìn)行優(yōu)化，又或者其他的優(yōu)化方法。但是都大同小異，核心是回溯的過程）：

//JAVA 
class Solution { 
    List<List<Integer>> ans = new ArrayList<>(); 
       
    public List<List<Integer>> permute(int[] nums) { 
        dfs(nums, new ArrayList<>()); 
        return ans; 
    }
    
    private void dfs(int[] nums, List<Integer> tmp) {
        System.out.println(Arrays.toString(nums) + "," + tmp);
        if (tmp.size() == nums.length) {
            ans.add(new ArrayList<>(tmp));
        } else {
            for (int num : nums) {
                if (!tmp.contains(num)) {
                    tmp.add(num);
                    dfs(nums, tmp);
                    tmp.remove(tmp.size() - 1);
                }
            }
        }
    }
    
}

假若 nums 為 [1,2,3]，會有下面的輸出：

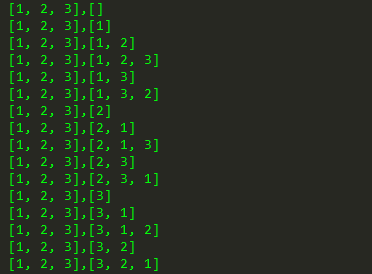
其實(shí)這個(gè)代碼還是很容易理解的，他干了個(gè)啥事？就是當(dāng)我們按順序去枚舉每一位時(shí)，我們要把已經(jīng)選擇過的數(shù)字排除掉（第16行代碼），比如我們上面選擇三個(gè)數(shù)字：

• 在枚舉第一位的時(shí)候，就有三種情況
• 在枚舉第二位的時(shí)候，就只有兩種情況（前面已經(jīng)出現(xiàn)的一個(gè)數(shù)字不可以再出現(xiàn)）
• 在枚舉第三位的時(shí)候，就只有一種情況（前面已經(jīng)出現(xiàn)的兩個(gè)數(shù)字不可以再出現(xiàn)）

整個(gè)代碼其實(shí)就干了這么一件事！而 第12行 的代碼，其實(shí)就是說當(dāng)枚舉到最后一位的時(shí)候，這個(gè)就是我們要的排列結(jié)果，所以我們要放入到全排列結(jié)果集中。

那這里還有一個(gè)很重要的代碼，其實(shí)是 第19行，這一步其實(shí)是干啥！說白了就是在回到上一位時(shí)，我們要就把上一次的選擇結(jié)果撤銷掉。不然如果你之前選過了，后面不就不能繼續(xù)用了么。

04、總結(jié)

回溯法（探索與回溯法）是一種選優(yōu)搜索法，又稱為試探法，按選優(yōu)條件向前搜索，以達(dá)到目標(biāo)。但當(dāng)探索到某一步時(shí)，發(fā)現(xiàn)原先選擇并不優(yōu)或達(dá)不到目標(biāo)，就退回一步重新選擇，這種走不通就退回再走的技術(shù)為回溯法，而滿足回溯條件的某個(gè)狀態(tài)的點(diǎn)稱為“回溯點(diǎn)”。

這是最簡單的一道全排列題目，注意我在上面的題解中，并沒有引入什么狀態(tài)、路徑、選擇列表、結(jié)束條件之類的專業(yè)術(shù)語，甚至我連回溯的概念都沒有提及。

之所以這樣講，我是希望咱可以從最簡單的人類思考出發(fā)，而不是去套用一些框架之類的東東。。。。當(dāng)然，至于更多的概念和回溯框架的東西，我會在后面更為復(fù)雜的題目中為大家引入。