如何求二維數(shù)組的前綴和?
前綴和是一種重要的預處理,能大大降低查詢的時間復雜度。我們可以簡單理解為“數(shù)列的前 n 項的和”。這個概念其實很容易理解,即一個數(shù)組中,第 n 位存儲的是數(shù)組前 n 個數(shù)字的和。
通過一個例子來進行說明會更清晰。題目描述:有一個長度為 N 的整數(shù)數(shù)組 A,要求返回一個新的數(shù)組 B,其中 B 的第 i 個數(shù) B[i]是「原數(shù)組 A 前 i 項和」。
這道題實際就是讓你求數(shù)組 A 的前綴和。對 [1,2,3,4,5,6] 來說,其前綴和可以是 pre=[1,3,6,10,15,21]。我們可以使用公式 pre[??]=pre[???1]+nums[??]得到每一位前綴和的值,從而通過前綴和進行相應的計算和解題。其實前綴和的概念很簡單,但困難的是如何在題目中使用前綴和以及如何使用前綴和的關系來進行解題。實際的題目更多不是直接讓你求前綴和,而是你需要自己「使用前綴和來優(yōu)化算法的某一個性能瓶頸」。
而如果數(shù)組是正數(shù)的話,前綴和數(shù)組會是一個單調不遞減序列,因此前綴和 + 二分也會是一個考點,不過這種題目難度一般是力扣的困難難度。關于這個知識點,我會在之后的「二分專題」方做更多介紹。
簡單的二維前綴和
上面提到的例子是一維數(shù)組的前綴和,簡稱一維前綴和。那么二維前綴和實際上就是二維數(shù)組上的前綴和了。一維數(shù)組的前綴和也是一個一維數(shù)組,同樣地,二維數(shù)組的前綴和也是一個二維的數(shù)組。
比如對于如下的一個二維矩陣:
1 2 3 4
5 6 7 8
定義二維前綴和矩陣 ,。經過這樣的處理,上面矩陣的二維前綴和就變成了:
1 3 6 10
6 14 24 36
那么如何用「代碼」計算二維數(shù)組的前綴和呢?簡單的二維前綴和的求解方法是基于「容斥原理」的。
比如我們想求如圖中灰色部分的和。
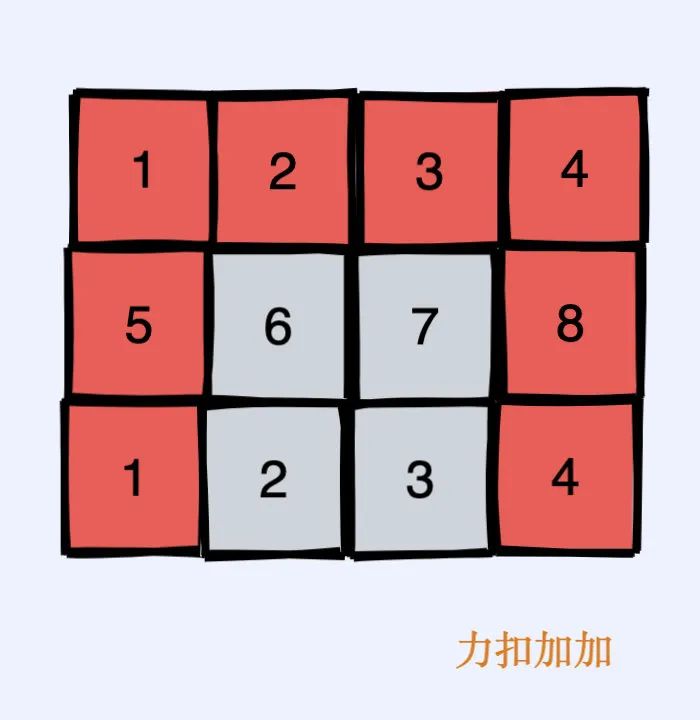
一種方式就是用下圖中兩個綠色部分的矩陣加起來(之所以用綠色部分相加是因為這兩部分已經通過上面預處理計算好了,可以在 的時間得到),這樣我們就會多加一塊區(qū)域,這塊區(qū)域就是如圖黃色部分,我們再減去黃色部分就好了,最后再加上當前位置本身就行了。
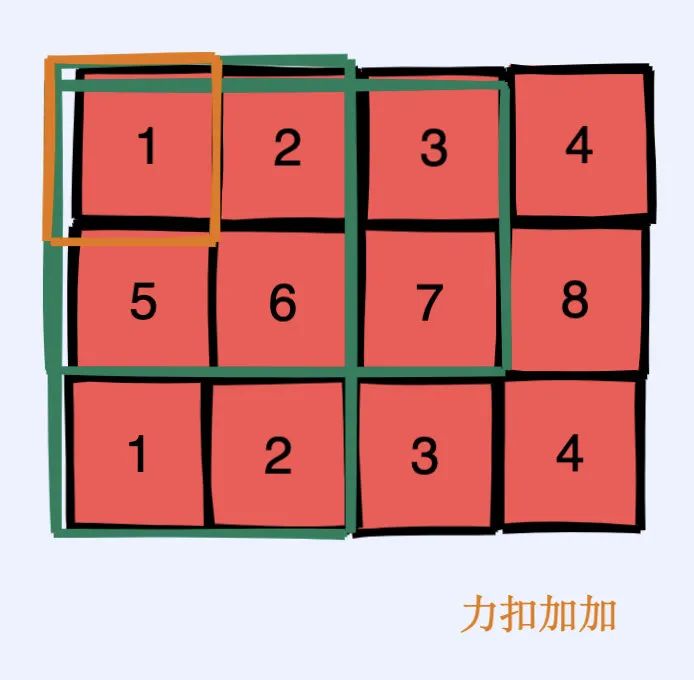
比如我們想要求 ,則可以通過 的方式來實現(xiàn)。這樣我就可以通過 的預處理計算二維前綴和矩陣(m 和 n 分別為矩陣的長和寬),再通過 的時間計算出「任意小矩陣的和」。其底層原理就是上面提到的容斥原理,大家可以通過畫圖的方式來感受一下。
如何將二維前綴和轉化為一維前綴和
然而實際上,我們也可不構建一個前綴和數(shù)組,而是直接原地修改。
?一維前綴和同樣可以采用這一技巧。
?
比如我們可以先不考慮行之間的關聯(lián),而是預先計算出每一行的前綴和。對于計算每一行的前綴和就是「一維前綴和」啦。接下來通過「固定兩個列的端點」的方式計算每一行的區(qū)域和。代碼上,我們可以通過三層循環(huán)來實現(xiàn), 其中兩層循環(huán)用來固定列端點,另一層用于枚舉所有行。
?其實也可以反過來。即固定行的左右端點并枚舉列,下面的題目會提到這一點。
?
代碼表示:
# 預先構建行的前綴和
for row in matrix:
for i in range(n - 1):
row[i + 1] += row[i]
比如矩陣:
1 2 3 4
5 6 7 8
則會變?yōu)椋?/p>
1 3 6 10
5 11 18 26
接下來:
# 固定列的兩個端點,即枚舉所有列的組合
for i in range(n):
for j in range(i, n):
pres = [0]
pre = 0
# 枚舉所有行
for k in range(m):
# matrix[k] 其實已經是上一步預處理的每一行的前綴和了。因此 matrix[k][j] - (matrix[k][i - 1] 就是每一行 [i, j] 的區(qū)域和。
pre += matrix[k][j] - (matrix[k][i - 1] if i > 0 else 0)
pres.append(pre)
上面代碼做的事情形象來看,就是先在水平方向計算前綴和,然后在豎直方向計算前綴和,而不是同時在兩個方向計算。
如果把 [i, j] 的區(qū)域和看出是一個數(shù)的話,問題就和一維前綴和一樣了。代碼:
for i in range(n):
for j in range(i, n):
pres = [0]
pre = 0
# 枚舉所有行
for k in range(m):
# 其中 a 為[i, j] 的區(qū)域和
pre += a
pres.append(pre)
題目推薦
有了上面的知識,我們就可以來解決下面兩道題。雖然下面兩道題的難度都是 hard,不過總體難度并不高。這兩道題之所以是 hard, 是因為其考察了「不止一個知識點」。這也是 hard 題目的一種類型,即同時考察多個知識點。
363. 矩形區(qū)域不超過 K 的最大數(shù)值和
題目地址
https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/
題目描述
給定一個非空二維矩陣 matrix 和一個整數(shù) k,找到這個矩陣內部不大于 k 的最大矩形和。
示例:
輸入: matrix = [[1,0,1],[0,-2,3]], k = 2
輸出: 2
解釋: 矩形區(qū)域 [[0, 1], [-2, 3]] 的數(shù)值和是 2,且 2 是不超過 k 的最大數(shù)字(k = 2)。
說明:
矩陣內的矩形區(qū)域面積必須大于 0。
如果行數(shù)遠大于列數(shù),你將如何解答呢?
前置知識
二維前綴和 二分法
思路
前面提到了由于非負數(shù)數(shù)組的二維前綴和是一個非遞減的數(shù)組,因此常常和二分結合考察。實際上即使數(shù)組不是非負的,我們仍然有可能構建一個有序的前綴和,從而使用二分,這道題就是一個例子。
首先我們可以用上面提到的技巧計算二維數(shù)組的前綴和,這樣我們就可以計算快速地任意子矩陣的和了。注意到上面我們計算的 pres 數(shù)組是一個一維數(shù)組,但矩陣其實可能為負數(shù),因此不滿足單調性。這里我們可以手動維護 pres 單調遞增,這樣就可以使用二分法在 的時間求出「以當前項 i 結尾的不大于 k 的最大矩形和」,那么答案就是所有的「以任意索引 x 結尾的不大于 k 的最大矩形和」的最大值。
之所以可以手動維護 pres 數(shù)組單調增也可得到正確結果的原因是「題目只需要求子矩陣和,而不是求具體的子矩陣」。
代碼上,當計算出 pres 后,我們其實需要尋找大于等于 pre - k 的最小數(shù) x。這樣矩陣和 pre - x 才能滿足 pre - x <= k,使用最左插入二分模板即可解決。
關鍵點
典型的二維前綴和 + 二分題目
代碼
語言支持:Python3
Python3 Code:
class Solution:
def maxSumSubmatrix(self, matrix: List[List[int]], K: int) -> int:
m, n = len(matrix), len(matrix[0])
ans = float("-inf")
for row in matrix:
for i in range(n - 1):
row[i + 1] += row[i]
for i in range(n):
for j in range(i, n):
pres = [0]
pre = 0
for k in range(m):
pre += matrix[k][j] - (matrix[k][i - 1] if i > 0 else 0)
# 尋找大于等于 pre - k 的最小數(shù),且這個數(shù)不能比 pre 大。比如 pre = 10, k = 3,就要找大于等于 7 的最小數(shù),這個數(shù)不能大于 10。
# 為了達到這個目的,可以使用 bisect_left 來完成。(使用 bisect_right 不包含等號)
idx = bisect.bisect_left(pres, pre - K)
# 如果 i == len(pre) 表示 pres 中的數(shù)都小于 pre - k,也就是說無解
if idx < len(pres):
# 由 bisect_left 性質可知 pre - pres[i] >= 0
ans = max(ans, pre - pres[idx])
idx = bisect.bisect_left(pres, pre)
pres[idx:idx] = [pre]
# 或者將上面兩行代碼替換為 bisect.insort(pres, pre)
return -1 if ans == float("-inf") else ans
「復雜度分析」
令 n 為數(shù)組長度。
時間復雜度: 空間復雜度:
題目給了一個 follow up:如果行數(shù)遠大于列數(shù),你將如何解答呢?實際上,如果行數(shù)遠大于列數(shù),由復雜度分析可知空間復雜度會很高。我們可以將行列兌換,這樣空間復雜度是 。換句話說,我們「可以通過行列的調換」做到空間復雜度為 。
1074. 元素和為目標值的子矩陣數(shù)量
題目地址
https://leetcode-cn.com/problems/number-of-submatrices-that-sum-to-target/
題目描述
給出矩陣 matrix 和目標值 target,返回元素總和等于目標值的非空子矩陣的數(shù)量。
子矩陣 x1, y1, x2, y2 是滿足 x1 <= x <= x2 且 y1 <= y <= y2 的所有單元 matrix[x][y] 的集合。
如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 兩個子矩陣中部分坐標不同(如:x1 != x1'),那么這兩個子矩陣也不同。
示例 1:
輸入:matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
輸出:4
解釋:四個只含 0 的 1x1 子矩陣。
示例 2:
輸入:matrix = [[1,-1],[-1,1]], target = 0
輸出:5
解釋:兩個 1x2 子矩陣,加上兩個 2x1 子矩陣,再加上一個 2x2 子矩陣。
提示:
1 <= matrix.length <= 300
1 <= matrix[0].length <= 300
-1000 <= matrix[i] <= 1000
-10^8 <= target <= 10^8
前置知識
二維前綴和
思路
和上面題目類似。不過這道題是求子矩陣和剛好等于某個目標值的「數(shù)目」。
我們不妨先對問題進行簡化。比如題目要求的是一維數(shù)組中,子數(shù)組(連續(xù))的和等于目標值 target 的數(shù)目。我們該如何做?
這很容易,我們只需要:
邊遍歷邊計算前綴和。 比如當前的前綴和是 cur,那么我們要找的前綴和 x 應該滿足 cur - x = target,因為這樣當前位置和 x 的之間的子數(shù)組和才是 target。即我們需要找前綴和為 cur - target 「的數(shù)目」。這提示我們使用哈希表記錄每一種前綴和出現(xiàn)的次數(shù)。
由于僅僅是求數(shù)目,不涉及到求具體的子矩陣信息,因此使用類似上面的解法求出二維前綴和。接下來,使用和一維前綴和同樣的方法即可求出答案。
關鍵點
主要考察一維前綴和到二維前綴和的過渡是否掌握
代碼
語言支持:Python3
Python3 Code:
class Solution:
def numSubmatrixSumTarget(self, matrix, target):
m, n = len(matrix), len(matrix[0])
for row in matrix:
for i in range(n - 1):
row[i + 1] += row[i]
ans = 0
for i in range(n):
for j in range(i, n):
c = collections.defaultdict(int)
cur, c[0] = 0, 1
for k in range(m):
cur += matrix[k][j] - (matrix[k][i - 1] if i > 0 else 0)
ans += c[cur - target]
c[cur] += 1
return ans
「復雜度分析」
時間復雜度: 空間復雜度:
和上面一樣,我們可以將行列對換,這樣空間復雜度是 。換句話說,我們「可以通過行列的調換」做到空間復雜度為 。
力扣的小伙伴可以關注我,這樣就會第一時間收到我的動態(tài)啦~
以上就是本文的全部內容了。大家對此有何看法,歡迎給我留言,我有時間都會一一查看回答。更多算法套路可以訪問我的 LeetCode 題解倉庫:https://github.com/azl397985856/leetcode 。目前已經 40K star 啦。大家也可以關注我的公眾號《力扣加加》帶你啃下算法這塊硬骨頭。
愛心三連擊
1.看到這里了就點個在看支持下吧,你的在看是我創(chuàng)作的動力。
2.關注公眾號力扣加加,帶你啃下算法這塊硬骨頭!加個星標,不錯過每一條成長的機會。
3.如果你覺得本文的內容對你有幫助,就幫我轉發(fā)一下吧。
