?LeetCode刷題實(shí)戰(zhàn)97：交錯(cuò)字符串

算法的重要性，我就不多說了吧，想去大廠，就必須要經(jīng)過基礎(chǔ)知識和業(yè)務(wù)邏輯面試+算法面試。所以，為了提高大家的算法能力，這個(gè)公眾號后續(xù)每天帶大家做一道算法題，題目就從LeetCode上面選 ！

今天和大家聊的問題叫做?交錯(cuò)字符串，我們先來看題面：

https://leetcode-cn.com/problems/interleaving-string/

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where they are divided into non-empty substrings such that:

s = s1 + s2 + ... + sn

t = t1 + t2 + ... + tm

|n - m| <= 1

The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...

Note: a + b is the concatenation of strings a and b.

題意

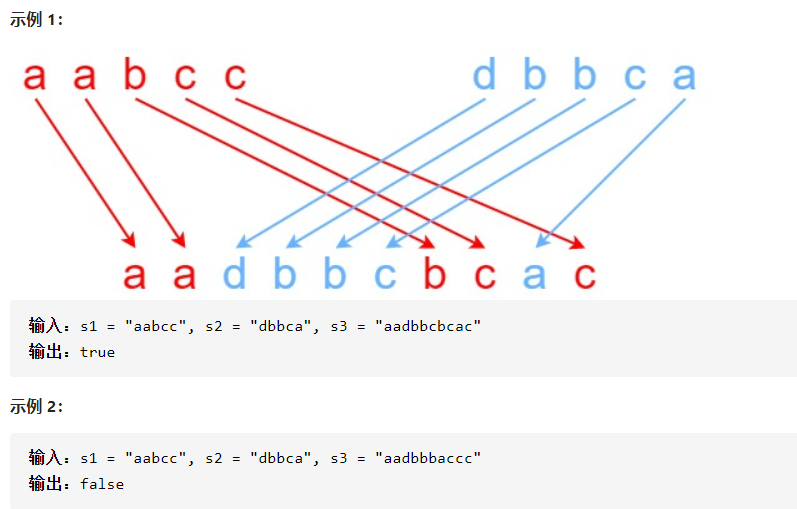
解題

https://my.oschina.net/u/3640932/blog/4405751

狀態(tài)定義

狀態(tài)轉(zhuǎn)移方程

狀態(tài)初始化

• dp[0][0] = True

• 如果 j = 0， dp[i][0] 是否成立，取決于 dp[i-1][0] 以及 s1 的第 i 個(gè)字符是否等于 s3 的第 i 個(gè)字符；

• 如果 i = 0， dp[0][j] 是否成立，取決于 dp[0][j-1] 以及 s3 的第 i 個(gè)字符與 s2 的第 i 個(gè)字符是否相等。

class Solution:
????def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
????????# 先處理特殊情況，如果 s1 和 s2 的長度和不等于 s3 的長度，則返回 False。因?yàn)闊o法交錯(cuò)拼接
????????if?len(s1) + len(s2) != len(s3):
????????????return?False
????????
????????m?= len(s1)
????????n = len(s2)

????????# 狀態(tài)定義
????????dp?= [[False] * (n+1) for?_ in range(m+1)]
????????# 初始化
????????dp[0][0] = True
????????for?i in range(1, m+1):
????????????dp[i][0] = dp[i-1][0] and?s3[i-1] == s1[i-1]
????????for?j?in range(1, n+1):
????????????dp[0][j] = dp[0][j-1] and?s3[j-1] == s2[j-1]

????????for?i in range(1, m+1):
????????????for?j?in range(1, n+1):
????????????????dp[i][j] = (dp[i-1][j] and?s3[i+j-1]==s1[i-1]) or?(dp[i][j-1] and?s3[i+j-1]==s2[j-1])

????????return?dp[-1][-1]