風控ML[4] | 風控建模的KS

我們這做風控模型的時候,經(jīng)常是會用KS值來衡量模型的效果,這個指標也是很多領導會直接關注的指標。今天寫一篇文章來全面地剖析一下這個指標,了解當中的原理以及實現(xiàn),因為這些知識是必備的基本功。我將會從下面幾個方面來展開講解一下KS:
KS的概念 KS的生成邏輯 KS的效果應用 KS的實現(xiàn)
01 KS的概念
KS的全稱叫“Kolmogorov-Smirnov“,我知道的是蘇聯(lián)數(shù)學家提出來的一個檢驗方法,后面怎么地就用到了風控模型的區(qū)分度評估就不知道咯。不過這不影響我們?nèi)ナ褂盟覀冎恍枰涝陲L控中是怎么實現(xiàn)的,并且在實際場景中怎么去使用它就可以了。就如上面我們說的,KS在風控主要是用于評估模型的好壞樣本區(qū)分度高低的。什么是區(qū)分度?通俗來說,就是模型預測結果排序分桶后,每個桶的好壞樣本占比的有排序性,也就是說不同的桶,壞人的識別能力都不同,我們可以通過“拒絕”壞人比較多的桶從而來實現(xiàn)風險控制。比較抽象?可以看下圖:
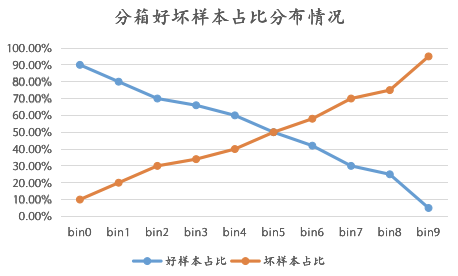
02 KS的生成邏輯
KS的生成邏輯公式也是十分簡單:
在風控領域,我們在計算KS前一般會根據(jù)我們認為的“正態(tài)分布原則”進行分箱,一般來說分成了10份,然后再進行KS的計算。具體的可以看下面的Demo:

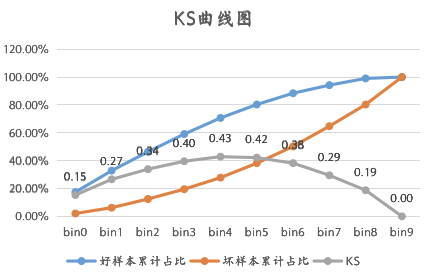
03 KS的效果應用
KS的值域在0-1之間,一般來說KS是越大越有區(qū)分度的,但在風控領域并不是越大越好,到底KS值與風控模型可用性的關系如何,可看下表:
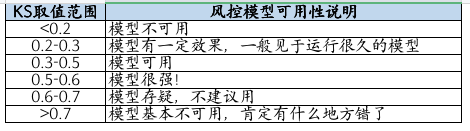
004 KS的實現(xiàn)
首先我們來對上面展示的例子進行Python代碼實現(xiàn)。
import?pandas?as?pd
import?numpy?as?np
#?test?data
bin_df?=?pd.DataFrame([['bin0',?100,?10],
???????????????????????['bin1',?100,?20],
???????????????????????['bin2',?100,?30],
???????????????????????['bin3',?100,?34],
???????????????????????['bin4',?100,?40],
???????????????????????['bin5',?100,?50],
???????????????????????['bin6',?100,?58],
???????????????????????['bin7',?100,?70],
???????????????????????['bin8',?100,?75],
???????????????????????['bin9',?100,?95]]
??????????????????????,columns=['bins',?'bin_nums',?'bad_nums'])
bin_df['good_nums']?=?bin_df.bin_nums?-?bin_df.bad_nums
bin_df['bad_rate']?=?bin_df.bad_nums/bin_df.bin_nums
bin_df['good_rate']?=?1?-?bin_df.bad_rate
bin_df['bad_cum']?=?bin_df.bad_nums.cumsum()
bin_df['good_cum']?=?bin_df.good_nums.cumsum()
bin_df['bad_cum_rate']?=?bin_df.bad_cum/bin_df.bad_nums.sum()
bin_df['good_cum_rate']?=?bin_df.good_cum/bin_df.good_nums.sum()
bin_df['cum_rate_dif']?=?abs(bin_df.bad_cum_rate?-?bin_df.good_cum_rate)
bin_df
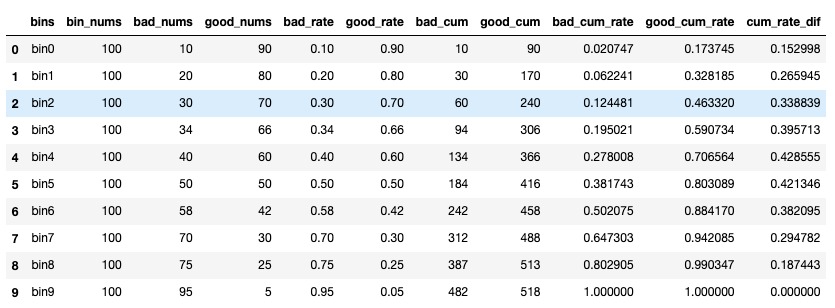
我們將數(shù)據(jù)進行一下可視化:
from?matplotlib?import?pyplot
import?matplotlib.pyplot?as?plt
print("KS:",?bin_df.cum_rate_dif.max())
plt.plot(bin_df.bins,?bin_df.bad_cum_rate,?marker='o',?mec='r',?mfc='w',?label='bad_cum_rate')
plt.plot(bin_df.bins,?bin_df.good_cum_rate,?marker='*',?mec='r',?mfc='w',?label='good_cum_rate')
plt.plot(bin_df.bins,?bin_df.cum_rate_dif,?marker='x',?mec='r',?mfc='w',?label='good_cum_rate')
plt.legend()

可以看到可視化的效果和我們在Excel里畫出來的差不多。
以上的代碼實現(xiàn)是基于分桶后的結果進行操作的,但是在大多數(shù)的情況下,都是不先進行分桶的,而是直接進行KS的計算,而計算KS的方式主要有兩種:
#?test?data
y_true?=?np.array([1,1,0,0,0,0,0,0,0,0])?#?真實標簽,0代表好人,1代表壞人
y_pred_proba?=?np.array([0.7,0.6,0.1,0.3,0.3,0.5,0.6,0.4,0.1,0.2])?#?模型預測概率結果,值域0-1,越大代表越解決壞人
#?way1
from?scipy.stats?import?ks_2samp
ks?=?ks_2samp(y_pred_proba[y_true?==?1],?y_pred_proba[y_true?==?0]).statistic
print("####?way1?####")
print("KS:",?ks)
#?way2
from?sklearn?import?metrics
fpr,?tpr,?thresholds?=?metrics.roc_curve(y_true,?y_pred_proba)
print("####?way2?####")
print("KS:",?max(tpr-fpr))
#?output
####?way1?####
KS:?0.875
####?way2?####
KS:?0.875
05 最后說一下
光看KS值來評估模型效果其實是不足夠的,就好像我們看一個人并不能光看臉,還得看身材、人品、才能等等,我們還需要看AUC、準確率、穩(wěn)定性、覆蓋率等等,這些后續(xù)都會陸續(xù)講到。今天我們就先了解清楚一下KS就可以了。
