【每日一題】Reflect.ownKeys 與 Object.keys 的區(qū)別

用法上

兩個(gè)函數(shù)都是接受一個(gè)對(duì)象參數(shù)，并都是以數(shù)組形式返回對(duì)象屬性的集合。

而且參數(shù)都必須是對(duì)象，如果是其他亂麻七糟的類(lèi)型，會(huì)報(bào)錯(cuò)

Reflect.ownKeys(targetObj)

Object.keys(targetObj)

不同之處

關(guān)于對(duì)象屬性是否可枚舉

Reflect.ownKeys()可以得到對(duì)象自己的所有屬性，包括不可枚舉屬性；
Object.keys()只能得到對(duì)象的普通可枚舉屬性，拿不到不可枚舉屬性。

關(guān)于Symbol屬性

Reflect.ownKeys()可以拿到對(duì)象的Symbol 的屬性；
Object.keys()不行。

關(guān)于數(shù)組的length屬性

因?yàn)?code style="overflow-wrap: break-word;padding: 2px 4px;border-radius: 4px;margin-right: 2px;margin-left: 2px;background-color: rgba(27, 31, 35, 0.05);font-family: "Operator Mono", Consolas, Monaco, Menlo, monospace;word-break: break-all;">Reflect.ownKeys()可以得到對(duì)象的不可枚舉屬性這個(gè)特點(diǎn)，所以當(dāng)目標(biāo)對(duì)象是數(shù)組對(duì)象時(shí)，我們可以看到獲取的結(jié)果會(huì)比Object.keys()多一個(gè)length屬性

事實(shí)證明，數(shù)組的length也確實(shí)是“不可枚舉的”：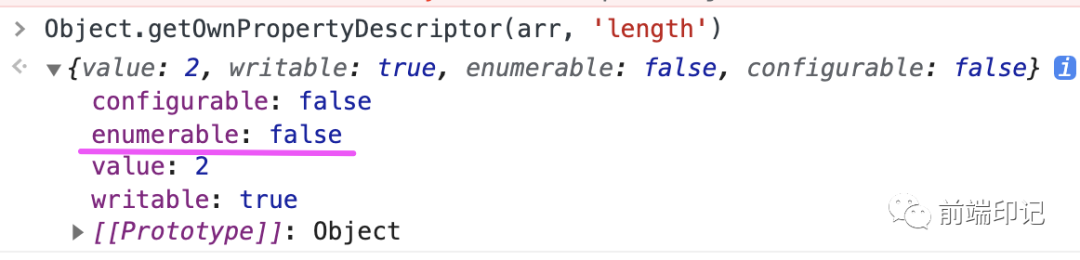

關(guān)于對(duì)象的原型

倆人這點(diǎn)上誰(shuí)也不比誰(shuí)強(qiáng)，都拿不到原型鏈上的屬性。

不過(guò)還好，這點(diǎn)需求上，可以用for...in來(lái)替代。

總結(jié)

分類(lèi)表格

整理一個(gè)看上去更清晰的表格如下（感謝群友給的靈感）

數(shù)組length其實(shí)就是不可枚舉屬性那一列的延伸。

測(cè)試代碼匯總：

Object.prototype.pr = "我是原型屬性"; // 原型上增加“pr”屬性
let s = Symbol();
let obj = {
  [s]: "this is Symbol", // 增加一個(gè)Symbol屬性“[s]”
  a: "a", // 一個(gè)普通屬性“a”
};
// 再定義一個(gè)不可枚舉的屬性“name”
Object.defineProperty(obj, "name", {
  value: "sunny",
  configurable: true,
  enumerable: false, // *
  writable: true,
});

// 觀察打印結(jié)果
console.log("Object.keys", Object.keys(obj)); // 只得到一個(gè)普通屬性：["a"]
console.log("Reflect.ownKeys(obj)", Reflect.ownKeys(obj)); // 得到普通屬性，以及symbol和不可枚舉屬性：["a", "name", Symbol()]

// 遺憾的是，二者都拿不到 原型上的屬性“pr”。我們用for in來(lái)獲取
for(let o in obj){
  console.log(o) // 分別打印：a、pr
}

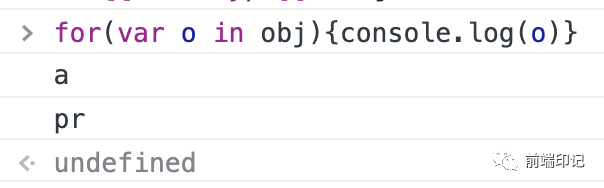
看來(lái)for in也不能獲取symbol屬性和不可枚舉屬性???♀?……