牛頓口中的巨人都有哪些人?
牛頓和胡克(身材矮小)之間因發(fā)現(xiàn)萬有引力定律的優(yōu)先權(quán)鬧得不愉快,在他們貌似紳士謙遜但暗藏譏諷的通信中牛頓說過一句話:
如果我比別人看得更遠(yuǎn),那是因?yàn)槲艺驹诰奕说募绨蛏稀?/p>
這話顯然在譏諷胡克,但的確也是事實(shí)。比如在物理上,牛頓的成就建立在伽利略、開普勒等巨人的研究上。
而本文想說的是在數(shù)學(xué)上,也就是在構(gòu)建微積分這個(gè)大殺器方面牛頓也不是從頭干起,那么這里頭是不是也有巨人呢?
回答是肯定的。
牛頓在讀大學(xué)那會(huì)兒,數(shù)學(xué)上很大程度是靠自學(xué)的。他學(xué)習(xí)了歐幾里得的《原本》、笛卡兒的《幾何》、沃利斯的《無窮算術(shù)》、巴羅的《數(shù)學(xué)講義》等許多數(shù)學(xué)家的著作。而牛頓自己說過對(duì)他影響巨大的要數(shù)笛卡兒的《幾何》和沃利斯的《無窮算術(shù)》。因?yàn)椋撬鼈儗⑴nD引導(dǎo)到當(dāng)時(shí)的前沿?cái)?shù)學(xué),解析幾何和幾何算術(shù)化。
我們不禁要問,從《原本》到《幾何》,歷經(jīng)近兩千年,這是數(shù)學(xué)知識(shí)積累后的突破,還是思想上的突破?
1 古希臘為什么沒有坐標(biāo)幾何?
我們知道,古希臘的幾何很厲害,但他們擅長于演繹邏輯,建立了公理化體系,為人類數(shù)學(xué)和科學(xué)建立了不世之功。
然鵝,他們的幾何為什么不包括坐標(biāo)幾何(解析幾何)呢?
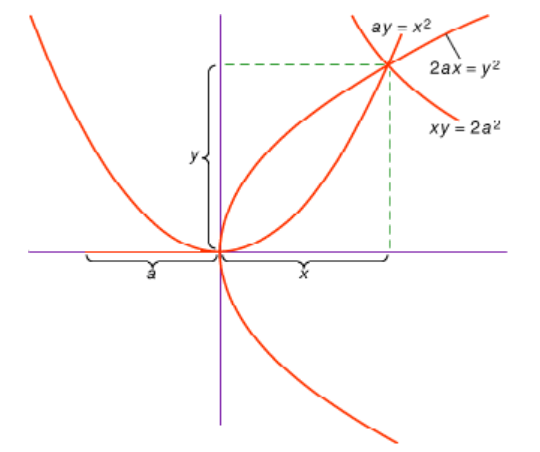
坐標(biāo)幾何的基本思想是用方程來表示曲線,希臘人則是利用曲線來研究代數(shù),例如梅內(nèi)克繆斯受希波克拉底處理倍立方體問題的啟發(fā),利用拋物線和雙曲線的交點(diǎn)得到 。
信仰萬物皆數(shù)的畢達(dá)哥拉斯強(qiáng)調(diào)數(shù)的比例論,然而由于不可公度的發(fā)現(xiàn),他們的理論遭受危機(jī)。
這也導(dǎo)致數(shù)的理論與幾何空間的理論之間的分裂,古希臘轉(zhuǎn)向幾何學(xué)。特別是在歐多克索斯提出以幾何量為基礎(chǔ)的比例理論后,在古希臘人看來,幾何比代數(shù)的邏輯基礎(chǔ)更加牢固。
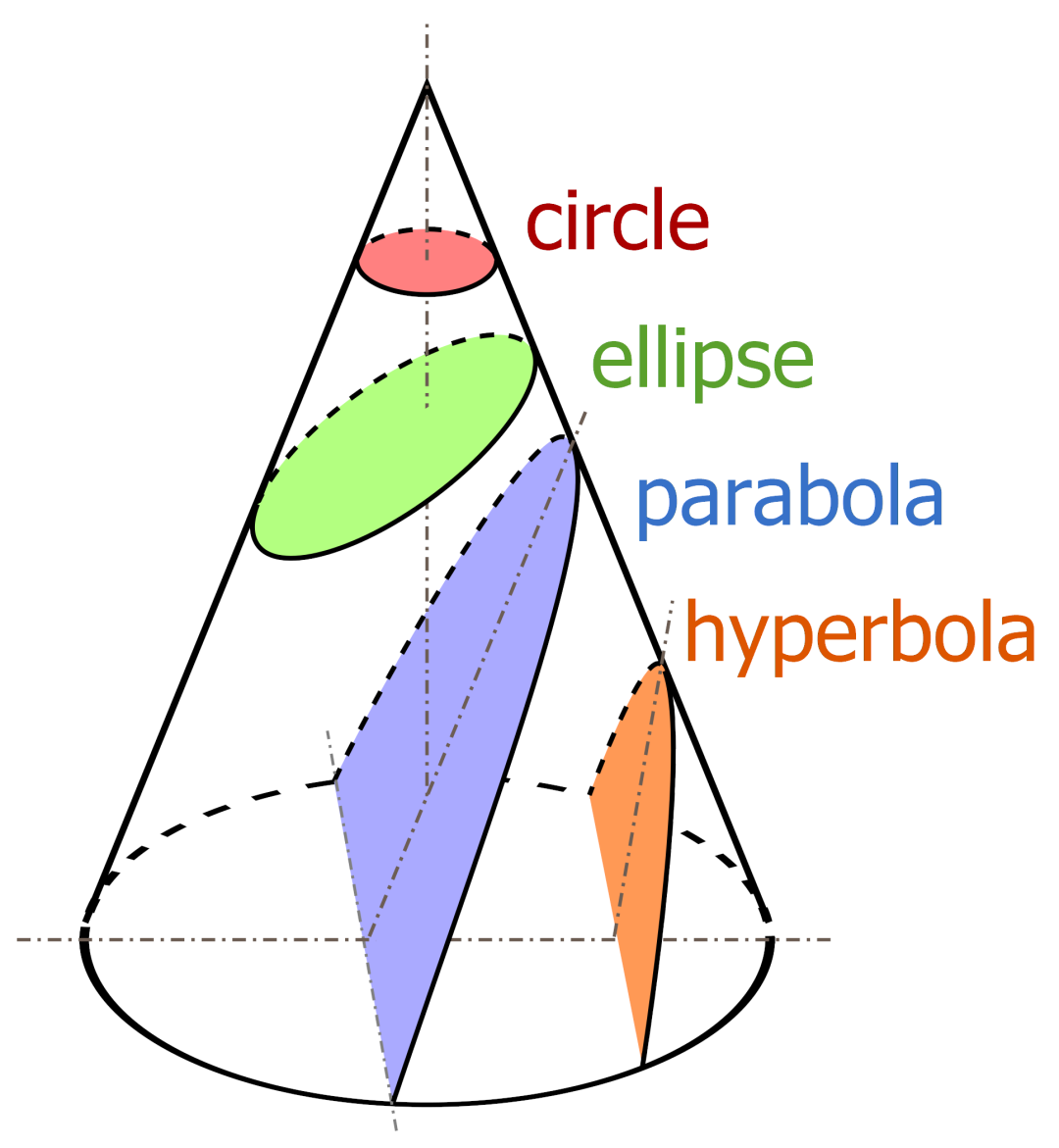
那么古希臘數(shù)學(xué)家在沒有坐標(biāo)的情況下是怎么研究圓錐曲線的?
希臘人偶然利用曲線來研究代數(shù),例如梅內(nèi)克繆斯受希波克拉底處理倍立方體問題的啟發(fā),發(fā)現(xiàn)圓錐曲線,并利用拋物線和雙曲線的交點(diǎn)得到 。后來,阿波羅尼奧斯在總結(jié)前人成果的基礎(chǔ)上完成了著名的大作《圓錐曲線論》。通過幾何量的比例,如長度的比例、面積的比例等來分析截線的幾何性質(zhì)。不是通過坐標(biāo)以及距離來計(jì)算的,因?yàn)樗麄兣懦獯鷶?shù)。雖然可以認(rèn)為本質(zhì)上是一致的,只是他們不使用數(shù),而是使用幾何量的比例,兩者之間被割裂。
2 笛卡爾的坐標(biāo)幾何
公元前 146 年,羅馬吞并希臘,幾百年后羅馬分裂成東、西兩個(gè)。
不知道咋肥事,數(shù)學(xué)的事情仿佛被按了暫停鍵。此時(shí)數(shù)學(xué),特別是代數(shù)在東方仍有發(fā)展,這對(duì)西歐數(shù)學(xué)會(huì)有一定影響。
直到 16 世紀(jì),力學(xué)方面的研究開始驅(qū)使數(shù)學(xué)家研究諸如重心之類的問題,才又開始恢復(fù)進(jìn)展。
荷蘭工程師斯蒂文(Simon Stevin,1548 - 1620),在計(jì)算三角形重心的過程中改進(jìn)了古希臘人的窮竭法,放棄歸謬法,使用極限思想;《靜力學(xué)原理》一書中,使用了平行四邊形法則。
意大利數(shù)學(xué)家瓦萊里奧(Valerio,1552 - 1618),運(yùn)用阿基米德法求各種旋轉(zhuǎn)體的重心和體積,重新燃起了人們對(duì)古希臘數(shù)學(xué)的熱情。
德國天文學(xué)家開普勒(Kepler,1571 - 1630)支持日心說,并從大量天文觀察數(shù)據(jù)中發(fā)現(xiàn)了行星運(yùn)動(dòng)三大定律。
我們來欣賞一下從地球上看到的各大行星在天球上的優(yōu)美舞姿(軌跡圖)。
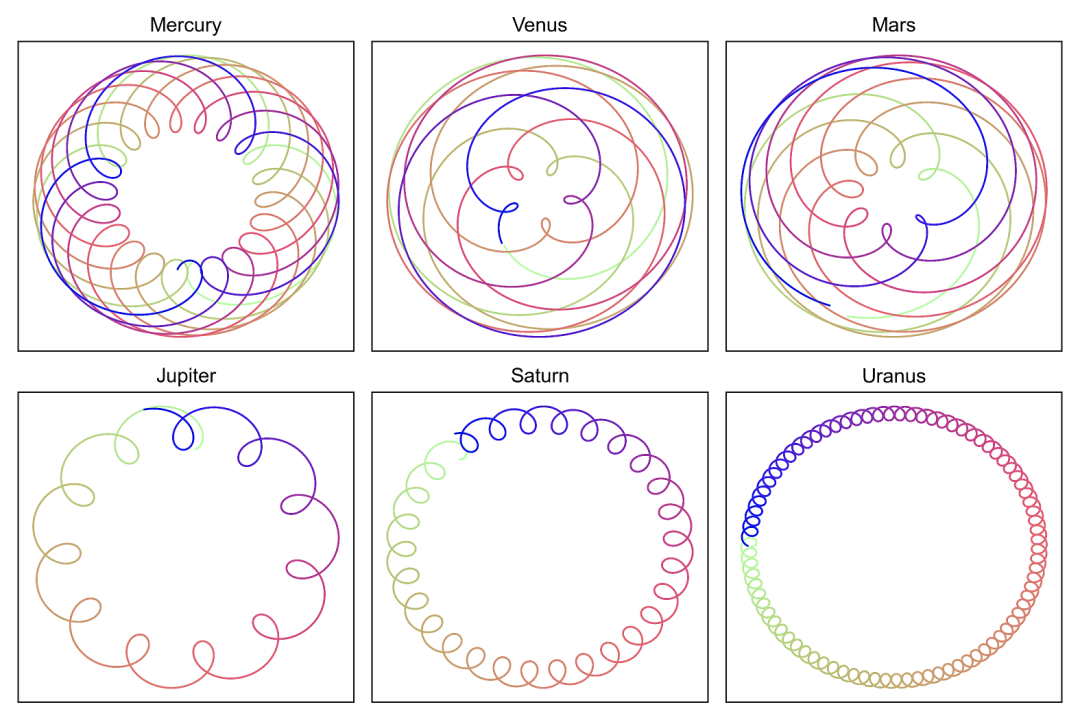
開普勒是幸運(yùn)的,前有日心說,又有前輩弟谷二十多年的高質(zhì)量觀測數(shù)據(jù)。開普勒內(nèi)心堅(jiān)信日心說,但又以數(shù)據(jù)說話,并不是拍腦袋認(rèn)為行星是圓周運(yùn)動(dòng)。他從這些復(fù)雜的運(yùn)行軌跡中挖掘出了行星的軌道圖形。
對(duì)的,開普勒配得上是最早一代數(shù)據(jù)挖掘大師。
他的第一定律就是橢圓軌道,第二定律是單位時(shí)間軌跡掃過面積恒定。在他關(guān)于行星運(yùn)動(dòng)的工作中,將橢圓的扇形面積視為線的總和,但這充其量算作一種樸素的、粗略的積分形式,開普勒并沒有像希臘人那樣作嚴(yán)謹(jǐn)思考。
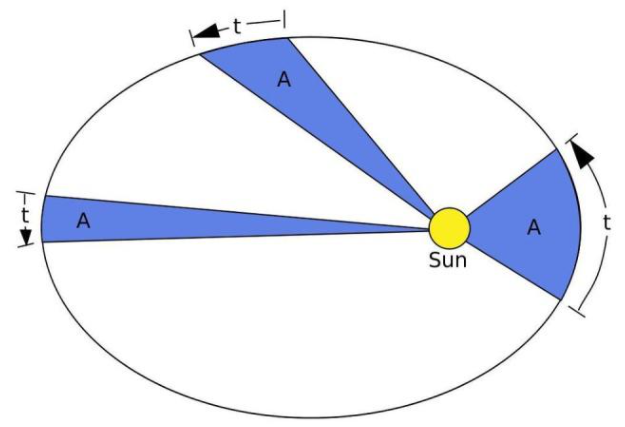
除了開普勒發(fā)現(xiàn)橢圓軌道外,意大利科學(xué)家伽利略(Galileo)也發(fā)現(xiàn)投擲物體會(huì)沿著拋物線運(yùn)動(dòng)。
這些在天文和力學(xué)方面的研究成果,進(jìn)一步激發(fā)了人們對(duì)曲線研究的熱情,代數(shù)學(xué)在這一階段得到了極大發(fā)展。通過代數(shù)方法尋求幾何問題的解決方案,成為研究曲線運(yùn)動(dòng)新的途徑。這在一定程度上也催生了坐標(biāo)幾何的登場。
? 坐標(biāo)幾何
在古希臘人看來,兩個(gè)數(shù)相加沒什么問題,這是基本的算術(shù)運(yùn)算,但一個(gè)量并不總是能加上另一個(gè)量。比如,一條線加上一個(gè)點(diǎn),或者一個(gè)體積加上一個(gè)面積,是沒有意義的,也就是說不該有像 這樣的式子。
比如,我們用 和 分別表示兩條線段的長度,那么 表示的是一個(gè)面積,此時(shí)式子 是什么意思呢? 兩條線段怎么能和一個(gè)面積相加呢? 再比如,三個(gè)量的乘積 可以被稱為體積,但是五個(gè)量的乘積 對(duì)應(yīng)什么幾何量呢?
也就是說,在他們看來只有相同類型的量才是可能相加的,而且還得對(duì)應(yīng)幾何量。這種對(duì)量的運(yùn)算加以限制的思想,即便到了韋達(dá)那里仍然殘留著。
笛卡爾的前輩,法國數(shù)學(xué)家韋達(dá)利用歐幾里得的《原本》第一個(gè)提出了無窮等比數(shù)列的求和公式,發(fā)現(xiàn)了正切定律、正弦差公式、純角球面三角形的余弦定理等,同時(shí)還發(fā)現(xiàn)了著名的韋達(dá)定理。韋達(dá)利用代數(shù)法分析幾何問題的思想,正是后繼者笛卡爾解析幾何思想的出發(fā)點(diǎn)。
在笛卡爾的墓碑上刻著這樣一句話:笛卡兒,歐洲文藝復(fù)興以來,第一個(gè)為人類爭取并保證理性權(quán)利的人。
為什么這么說呢?作為理性主義的代表人物,有別于經(jīng)驗(yàn)主義者,笛卡爾堅(jiān)信可以用數(shù)學(xué)撬開宇宙奧秘。在這點(diǎn)上,他邁出了重要的一步。
簡而言之,笛卡爾通過引入單位 1,輕巧地打破了對(duì)量運(yùn)算在思維上的限制。進(jìn)而他引入了現(xiàn)在稱為坐標(biāo)系的思想來展示如何使用代數(shù)來解決幾何問題。
笛卡爾和很多前輩一樣,將代數(shù)方程不是當(dāng)作純數(shù)的運(yùn)算,而是指幾何量的運(yùn)算,用幾何術(shù)語來解釋所有代數(shù)運(yùn)算。
為了充分利用代數(shù)的力量,笛卡爾必須想出辦法克服古希臘的思維限制,即在一定意義上必須與過去進(jìn)行重大決裂。他為代數(shù)方程發(fā)明了一種新的幾何解釋,使代數(shù)學(xué)家擺脫了無法寫出 或 等嚴(yán)重限制。他解放了自己,因此也解放了他的繼任者,包括現(xiàn)在的我們。
笛卡爾選擇了一條他稱之為單位長度的線段,長度為 ,可以任意選擇。這讓他將符號(hào) 解釋為一個(gè)矩形的面積,其中一條邊的長度為 ,另一條邊的長度為 。這樣,他就可以放心地寫出 ,因?yàn)樗梢员徽J(rèn)為是兩個(gè)面積的總和。
更重要的是,他將乘積解釋為線的長度,因此他可以將任意冪解釋為線的長度。也就是說,笛卡爾的線段 和 的乘積不一定是面積 ,但可以是另一個(gè)長度,例如
并且,還可以把長度 構(gòu)造出來,如下圖所示。
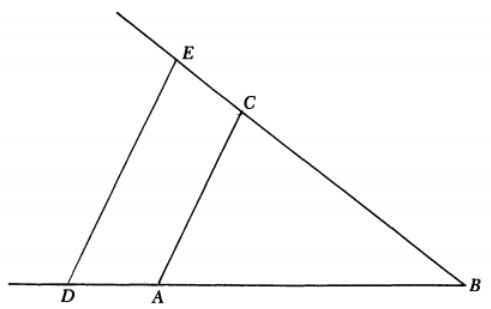
在這個(gè)例子中,給定一個(gè)單位線段 ,構(gòu)造 和 的乘積。讓線段 和 在起始于 的同一條線上下線,讓線段 延伸并構(gòu)造平行于 的 ,從而產(chǎn)生比例 (因?yàn)? )。因此 就是要的乘積 。
當(dāng)然這是一個(gè)簡單的構(gòu)造,但他必須明確給出。笛卡爾的幾何哲學(xué)并沒有讓他僅僅斷言一條線段長度等于兩條線段長度的乘積,他還需要構(gòu)建它。
笛卡爾在他的著作《幾何》中分析了當(dāng)時(shí)的幾何學(xué)與代數(shù)學(xué)各自的優(yōu)缺點(diǎn)。他認(rèn)為希臘人的幾何過多地依賴于圖形,而代數(shù)學(xué)卻完全受法則和公式的限制,以至于阻礙了自由的思想和創(chuàng)造力。
但是,笛卡爾在《幾何》中使用的潛在的坐標(biāo)系中都僅有一個(gè)坐標(biāo)軸是明確的。在 1649 年 Frans van Schooten 及其學(xué)生將《幾何》譯成拉丁文時(shí),為闡釋其中的一些想法而引入了一些概念,包括第二個(gè)坐標(biāo)軸。
題外 使用字母 來表示末知量據(jù)說源于一個(gè)巧合事件。《幾何》在排版時(shí),打字員發(fā)現(xiàn)字母表的最后幾個(gè)字母不夠用了。他問笛卡兒,書中諸多方程中使用字母 還是 是否有關(guān)系。笛卡兒回答說,用哪個(gè)字母表示末知量都行。于是這個(gè)打字員就選擇 ,因?yàn)樽帜? 和 在法語中的使用頻車要高于 。
3 曲線下的面積
前面說了,開普勒進(jìn)一步激發(fā)了大家對(duì)曲線下的面積的計(jì)算熱情。在這個(gè)問題上,三位年齡相仿的數(shù)學(xué)家相繼發(fā)力,他們是意大利數(shù)學(xué)家卡瓦列里(Cavalieri,1598 - 1647)、法國業(yè)余數(shù)學(xué)家費(fèi)馬(Fermat,1601 - 1665)和法國數(shù)學(xué)家羅伯瓦爾(Roberval,1602 - 1675)。
開普勒對(duì)積分的嘗試啟發(fā)了卡瓦列里,他展示了 從 到 的積分是 ,通過計(jì)算多個(gè) 值的結(jié)果后推斷出一般結(jié)果。
卡瓦列里最大的貢獻(xiàn)是建立了祖暅原理(又名等冪等積定理,西方稱為卡瓦列里原理),依靠這個(gè)原理,他求得相當(dāng)于曲線 下的面積。
此處插播一個(gè)作業(yè),那就是需要計(jì)算如下級(jí)數(shù),
阿拉伯?dāng)?shù)學(xué)家 Al-Haytham(965 - 1040)發(fā)現(xiàn)了 時(shí)的求和公式,并用它來計(jì)算拋物面的體積。
而卡瓦列里將公式推廣到 ,然后猜想更一般的情況同樣成立。
該公式可以用于計(jì)算某些立體的體積,甚至超越了阿基米德和開普勒的成績。
由此還引發(fā)了以面積計(jì)算體積的方法并成為了積分發(fā)展的一個(gè)重要步驟。
羅伯瓦爾考慮了相同類型的問題,但比卡瓦列里要嚴(yán)格得多。
羅伯瓦爾認(rèn)為曲線和直線圍成的面積是由無數(shù)個(gè)無限窄的矩形條組成的。
他將這個(gè)想法應(yīng)用于 ,計(jì)算從 到 的積分,聲稱得到近似值,
羅伯瓦爾然后斷言當(dāng) 趨向于無窮大時(shí)上式趨向于 ,由此算得面積。
有興趣的不妨用下面公式驗(yàn)證一下上面羅伯瓦爾的結(jié)論。
比如 ,上式兩邊同時(shí)除以 ,得
當(dāng) 取值越大,矩形就越多,它們的面積之和就越接近曲線圍成的面積。
因此,當(dāng) 趨向于無窮大時(shí),上式等于 ,直覺告訴我們這就是這些矩形的面積之和,它應(yīng)該也等于曲線圍成的面積。
而費(fèi)馬的方法相對(duì)而言更加嚴(yán)謹(jǐn)一些,但同樣地也沒有給出相應(yīng)證明。
他還推廣了拋物線和雙曲線,
- 從拋物線 推廣到,
- 從雙曲線 推廣到,
? 切線和極值
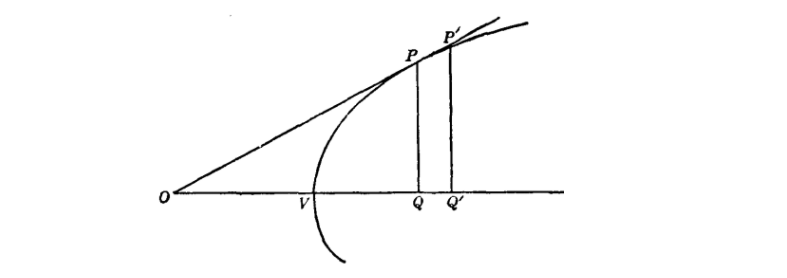
費(fèi)馬不僅對(duì)解析幾何有貢獻(xiàn),更是一位熱衷于無窮小分析的好手,他大概是為了求極大、極小值問題引入了后來稱為導(dǎo)數(shù)的概念。他寫信給笛卡爾,給出了今天使用的方法,即通過計(jì)算函數(shù)的導(dǎo)數(shù)何時(shí)為 來找到極大值和極小值。
他認(rèn)為他的求切線方法是他的求極值方法的一個(gè)應(yīng)用。下圖是他對(duì)拋物線上的點(diǎn) 求切線的做法。他令 趨于無窮小時(shí)得到切線方程。
除了導(dǎo)數(shù),費(fèi)馬也觸摸到了微分與積分之間的關(guān)系,這主要源自對(duì)于曲線求長度的問題。
大概在 1660 年前不久,出現(xiàn)了一些曲線求長度的方法,一般是用多邊形去逼近曲線,然后應(yīng)用無窮小量或極限來處理的。費(fèi)爾馬得知這些方法以后,自己搞了一個(gè)求半立方拋物線長度的方法。他的這一做法是他的一般方法的典型,并很好地表示出他的工作中各方面的內(nèi)在聯(lián)系。
對(duì)曲線上橫坐標(biāo) 、縱坐標(biāo) 的任一點(diǎn),次切線 可以用他的切線方法求得為 ?。于是在離縱坐標(biāo) 距離 處取切線的縱坐標(biāo) ,則線段 可以用 和 來表達(dá)。
舉個(gè)具體例子,對(duì)曲線 來說,有 ,即曲線長度的增量,這個(gè)相當(dāng)于后來記為 的東西。在費(fèi)馬看來,當(dāng) 很小時(shí), 可以看作不但在切線上,而且也在曲線上,所以曲線的長度可以視為 的線段的和。這里需要發(fā)揮一下洞察力,這些線段的和又可以作為曲線 圍成的面積,用現(xiàn)在的寫法就是,
由于這個(gè)面積已經(jīng)能夠求出,因此曲線長度自然也可以求得。
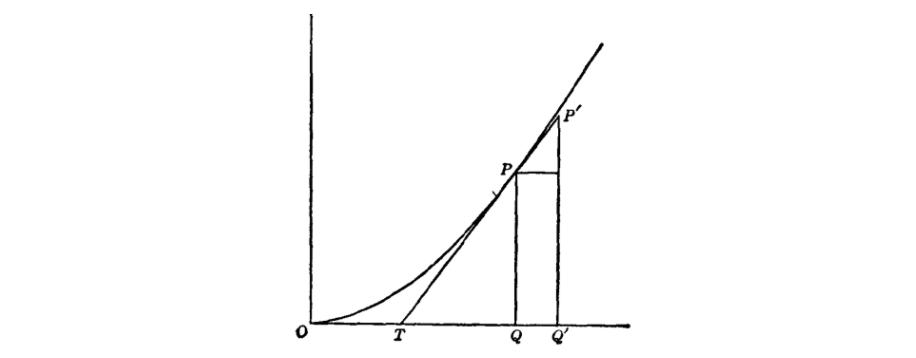
奇怪的是,費(fèi)馬用他的極大極小值方法來求重心,他將與切線有關(guān)的曲線求長問題化為一個(gè)求面積的問題,他從幾何和解析的角度在各種問題上應(yīng)用了無限小量,竟然會(huì)象帕斯卡一樣,沒有看到這兩類問題之間的基本聯(lián)系。
費(fèi)馬在這些問題中用過一些示圖。這些示圖和帕斯卡所用的,非常相象,這就是后來萊布尼茨感到對(duì)他的微分三角形深有啟發(fā)的那張圖,可是費(fèi)馬還沒有覺察到它們的深遠(yuǎn)意義。
只要費(fèi)馬能對(duì)他的拋物線和雙曲線求切線和求面積的結(jié)果更仔細(xì)地考察一下,他是可能會(huì)發(fā)現(xiàn)微積分的基本定理,并如他有時(shí)被不恰當(dāng)?shù)胤Q呼的那樣,成為微積分的真正的發(fā)明者。
費(fèi)馬當(dāng)然在某種意義下理解到這兩類問題有一個(gè)互逆關(guān)系。他之所以沒有作進(jìn)一步的考慮,可能是由于他以為他的工作只是求幾何問題的解,而不是代表一種本身就很有意義的推理過程。
他的極大、極小值方法,切線方法以及求面積方法,在他看來是為解決這些問題而特有的方法,不是新的分析學(xué)。
此外,它們在應(yīng)用上顯然是有局限性的。費(fèi)馬只知道怎樣應(yīng)用它們到有理式的情況,而牛頓和萊布尼茲通過無窮級(jí)數(shù)的應(yīng)用,認(rèn)識(shí)到這些方法的普遍性。然而,除了巴羅以外,可能沒有數(shù)學(xué)家如費(fèi)馬這樣接近地醞釀微積分的發(fā)明。拉格朗日甚至認(rèn)為費(fèi)馬是微積分的發(fā)明者。
4 沃利斯與《無窮算術(shù)》
笛卡爾引入坐標(biāo)思想,將數(shù)和形之間被割裂的關(guān)系重新彌合起來。但他主要是打通兩者,便于用代數(shù)去研究幾何,并沒有想將幾何建立在代數(shù)的基礎(chǔ)上。
而幾何算術(shù)化的思想可以說是英國數(shù)學(xué)家沃利斯首先引入的,他用笛卡爾的坐標(biāo)思想,從古希臘的截圓錐給出的定義導(dǎo)出方程,然后反過來用這些方程導(dǎo)出曲線的性質(zhì),之后完全擺脫對(duì)圓錐的依賴了。

沃利斯(Wallis,1616 - 1703)是一位對(duì)牛頓影響非常大的英國數(shù)學(xué)家。
由于他與后面牛頓等人的工作有直接關(guān)系,我們此處簡述一下沃利斯的主要成就。
一般來說,沃利斯是最早把圓錐曲線當(dāng)作二次曲線加以討論的人,從此擺脫了過去將圓錐曲線視為圓錐截線的純幾何觀念。
沃利斯在笛卡爾的基礎(chǔ)上大膽引進(jìn)了負(fù)的坐標(biāo)值,實(shí)現(xiàn)圓錐曲線的算術(shù)化,對(duì)完善和傳播坐標(biāo)幾何的思想起了重要作用。
他的《無窮算術(shù)》一書,本質(zhì)上是以算術(shù)的方式大大擴(kuò)展了卡瓦列里的不可分原理。
在這本書中他甚至還提出了極限的初步概念:變量的極限,是變量能如此逼近的一個(gè)常數(shù),使它們之間的差能夠小于任何給定的量。
這個(gè)定義雖然還不夠嚴(yán)密,但卻向極限的精確定義邁進(jìn)了重要的一步。
牛頓曾說:大約在我的數(shù)學(xué)生涯初期,那時(shí)我們杰出的同胞沃利斯博士的著作剛剛落入我的手里,他考慮到級(jí)數(shù),用級(jí)數(shù)插入法求出了圓與雙曲線的面積。
因此,美國數(shù)學(xué)史家波耶(Boyer)說:
牛頓承認(rèn)他在分析和流數(shù)方面的第一次發(fā)現(xiàn),是受沃利斯的《無窮算術(shù)》的啟發(fā)。
說了一堆文字,我們來看點(diǎn)算術(shù)化涉及到的實(shí)實(shí)在在的式子。
沃利斯推廣了整數(shù)冪的運(yùn)算,將指數(shù)的定義從正整數(shù)擴(kuò)充至有理數(shù),即包括 、負(fù)數(shù)以及分?jǐn)?shù)。
-
,,,
-
為 的開方, 的開立方,
-
為 的開 次方。
-
為 的開 次方。
他首次引進(jìn)了沿用至今的無窮大記號(hào) 。
-
沃利斯首先發(fā)表了提出拋物線、橢圓和雙曲線的代數(shù)公式的工作,這是笛卡爾開創(chuàng)性工作的重大進(jìn)展。
-
沃利斯將圓錐曲線從圓錐中解放出來的目的之一是為了尋找一種計(jì)算曲線下面積的通用方法。
他在《無窮算術(shù)》中具體討論了這種方法。
他用代數(shù)方法計(jì)算了 的積分,即曲線 下的面積,證明這個(gè)面積是等高等底的平行四邊形(未規(guī)定使用直角坐標(biāo)系)的面積的 。
可以理解,他的一些結(jié)果跟別人已得出的結(jié)果是等價(jià)的。
例如,對(duì)正整數(shù) ,可以證明當(dāng) 時(shí),有
從而得出,
沃利斯認(rèn)為代數(shù)方法的簡明并不遜于幾何的直觀,因此他更喜歡使用代數(shù)方法,并且使代數(shù)擺脫對(duì)幾何的依賴。
然后更進(jìn)一步,他給出了處理分?jǐn)?shù)次冪的新途徑,他直接去求 ,而不再像費(fèi)馬做過的那樣去考慮曲線 。
他首先求出了 ,,,辦法是考慮跟 ,, 曲線下面積互補(bǔ)的面積,然后通過跟已得結(jié)果得出其它分?jǐn)?shù)次冪的結(jié)果。
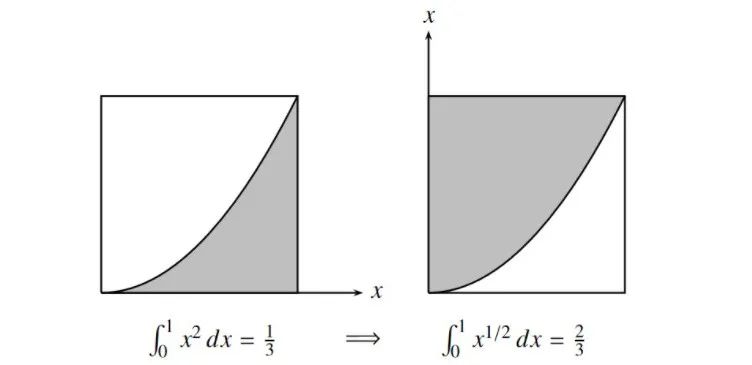
然而,有一點(diǎn)不得不說:沃利斯的推理按今天的標(biāo)準(zhǔn)來看,是極端不嚴(yán)謹(jǐn)?shù)摹?/strong>
例如,他會(huì)根據(jù)對(duì) 觀察到的一種模式,便根據(jù)歸納法宣布一個(gè)對(duì)所有正整數(shù) 均成立的公式,甚至根據(jù)插值法宣布對(duì) 為分?jǐn)?shù)時(shí)也成立。
他的大膽有個(gè)好處,就是可以導(dǎo)出一些了不起的公式,例如他著名的無限乘積公式。
沃利斯雖然引進(jìn)了分?jǐn)?shù)次冪,并且計(jì)算了一些某些冪次曲線的面積,但有一條大家熟悉的曲線的面積難住了他。
那就是圓的面積,其方程為 ,因?yàn)樗麩o法將其展開為 的冪級(jí)數(shù)。然而,他制定了插值原理。
沃利斯試圖將他的方法用來計(jì)算圓的面積,即四分之一圓對(duì)應(yīng)的曲線,
此時(shí)指數(shù)是分?jǐn)?shù),這其實(shí)要用到廣義二項(xiàng)式定理,但他似乎沒有考慮這個(gè)問題,因此在計(jì)算圓面積這個(gè)問題上碰到了麻煩。
然而,他發(fā)現(xiàn)圓 的縱坐標(biāo)是曲線 和 的縱坐標(biāo)的幾何平均值。
這時(shí),他想到了插值法,將 半圓的面積取為 和 的兩個(gè)積分值的幾何平均值,當(dāng)然這只是作為近似值。
即 和 的幾何平均值;這相當(dāng)于將 作為 的值。
當(dāng)然,沃利斯顯然不滿足于這樣的結(jié)果。
他繼續(xù)琢磨,終于想到一個(gè)法子。
牛頓極有很可能是受此方法的啟發(fā)而發(fā)現(xiàn)了廣義二項(xiàng)式定理,因此,我們有必要來看一看沃利斯的這個(gè)方法。
首先,沃利斯把問題統(tǒng)一成如下形式,
其中, 和 都是整數(shù)。
沃利斯發(fā)現(xiàn)上述積分總是某個(gè)整數(shù)的倒數(shù),即 ,
例如, 和 時(shí),有
沃利斯為了找出規(guī)律,便計(jì)算各種 的組合,并將它們的 值制成一個(gè)表。
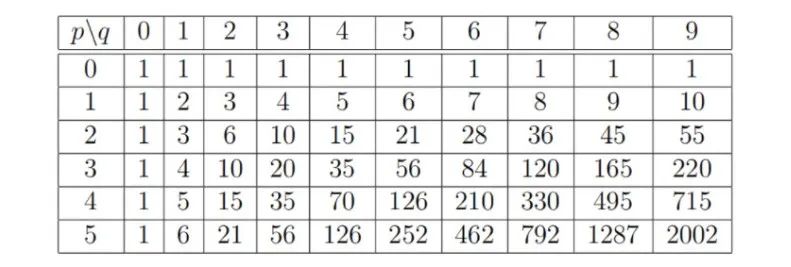
實(shí)際上,沃利斯計(jì)算了比上面更多的情況,因?yàn)樗Mㄟ^這張表發(fā)現(xiàn)一個(gè)用 和 表示的通用公式。
另外,他想著如果當(dāng) 和 不是整數(shù)時(shí),這個(gè)公式仍然成立的話,他可以代入 ,那豈不是可以計(jì)算想要的答案了,
理想是美好的,現(xiàn)實(shí)也還湊合。
他也確實(shí)發(fā)現(xiàn)了一些規(guī)律,那就是,
例如,在第 2 行中的值為,
以及第 3 行,
問題是沃利斯想要計(jì)算的是 ,代入前面已經(jīng)發(fā)現(xiàn)的公式,得
這什么東東,分?jǐn)?shù)的階乘!?沃利斯那年代還沒有這個(gè)玩意兒。
但作為數(shù)學(xué)家,豈能被這點(diǎn)事情難倒?
沃利斯自然是不畏縮的,他繼續(xù)想辦法制表。
什么辦法呢?其實(shí)就是根據(jù)已知去猜未知,這可是有學(xué)名的,叫插值法。
我們來看看這個(gè)表,
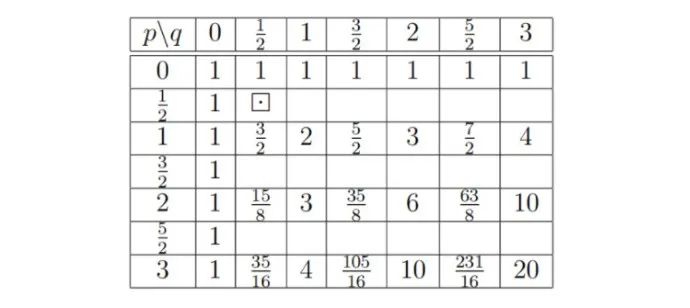
這個(gè)時(shí)候他不管三七二十一,假設(shè) 為整數(shù),將 設(shè)為分?jǐn)?shù)代入前面的式子,比如,
沃利斯在這里純粹是試探性的,他不確定當(dāng) 或 不是整數(shù)時(shí),上述公式是否仍然對(duì)應(yīng)相應(yīng)的積分值。
幸運(yùn)的是,他竟然猜對(duì)了,然后他得到了公式,即
簡單總結(jié)就是:能算的把它們算出來,找出規(guī)律得到公式,算不了的就強(qiáng)行代入這個(gè)公式去算,這就算插值!
上面是一個(gè)遞歸公式,但至少兩邊對(duì)于任何數(shù)字 都是有意義的。
同樣,沃利斯只知道這個(gè)公式在整數(shù)的情況下是成立的,然后他假設(shè)對(duì)于非整數(shù)也是正確的。
這樣子,他就可以大膽地在任意行中向右填充。例如,在 行中,他得到
像這樣繼續(xù)下去,他最終完成了 那一行的值,具體如下所示,

其中,,也就是,
還記得前文說過表中這些值是積分的倒數(shù)嗎?隨著 的增加,積分會(huì)變小,因此這些值會(huì)變大。
于是由上面表中的最后三項(xiàng)可得,
將 代入,得
兩邊夾逼之下,隨著 的增大,這個(gè)連乘積將收斂。
通過這種方式,沃利斯得到了如下令人超級(jí)吃驚的連乘公式,
好了,沃利斯的插值實(shí)驗(yàn)到此告一段落。
為什么要說這個(gè)事情呢?對(duì)微積分的誕生很重要嗎?
也不算是,但是,可能對(duì)牛頓的影響比較大:一方面是處理分?jǐn)?shù)次冪,另一方面可能也教會(huì)了牛頓去大膽地猜。
我們很快會(huì)看到,牛頓貌似也確實(shí)學(xué)到了這一招。
這么做不是簡單地猜,或者說歸納。背后有我的想法,那就是對(duì)連續(xù)性的信念。自然數(shù)不是孤立的,有分?jǐn)?shù)、負(fù)數(shù),甚至有復(fù)數(shù),我接受這些數(shù)的合法地位,因此我相信它們可以遵循同一個(gè)規(guī)律,所以我敢將它們代入同一個(gè)公式。
? 橢圓
最后,不知道大家有沒有想過,古人是如何定義橢圓的?
首先,遺憾的是,我國古代一直沒有認(rèn)識(shí)到橢圓曲線。而古希臘人我們已經(jīng)說過是通過截取圓錐得到的橢圓。但是橢圓軌跡的方程呢?是怎么來的呢?
我們來看一下沃利斯對(duì)橢圓的定義:

沃利斯首次采用代數(shù)語言將橢圓定義為具有性質(zhì) 的平面圖形,其中 為直徑, 為通徑(過焦點(diǎn)且垂直于長軸的弦長), 為橢圓上任意一點(diǎn)的坐標(biāo)。沃利斯的定義并沒有為后人直接采用,而他為橢圓標(biāo)準(zhǔn)方程的確立開了一個(gè)頭。
早在古希臘,橢圓的原始定義建立在立體圖形上,需要一定的空間想象。而橢圓的平面性質(zhì),如焦半徑性質(zhì)已經(jīng)為阿波羅尼斯所發(fā)現(xiàn),但直到 17 世紀(jì),人們才逐漸摒棄橢圓的原始定義,歷史同樣驚人地跨越了漫長的兩千年!
盡管古希臘人已經(jīng)將圓錐曲線看作軌跡,但在坐標(biāo)幾何誕生之前,將曲線看成軌跡并不是研究曲線性質(zhì)的前提,人們似乎并不需要采用新定義。只有在坐標(biāo)幾何誕生之后,需要將曲線看作動(dòng)點(diǎn)的軌跡以建立其方程,或根據(jù)方程研究曲線的性質(zhì),而不再依賴幾何語言和幾何方法。
最后再提一下,在當(dāng)時(shí)以及包括后來的牛頓萊布尼茲時(shí)代,對(duì)數(shù)學(xué)(特別是分析)的論證遠(yuǎn)沒有那么嚴(yán)謹(jǐn)。我們將很快見識(shí)到牛頓沿著沃利斯的步法叩開微積分大門。
休息一下,未完待續(xù)
