Python中堪稱神仙的6個(gè)內(nèi)置函數(shù)

人生苦短，快學(xué)Python！

大家好，我是小五。之前給大家分享過3個(gè)節(jié)省時(shí)間的Python技巧，當(dāng)時(shí)就提出了，大家可以多使用Python的內(nèi)置函數(shù)，既能提高自己的Python程序速度，同時(shí)還能保持代碼簡(jiǎn)潔易懂。

今天，它們就來了，我們會(huì)一次性分享6個(gè)堪稱神仙的內(nèi)置函數(shù)。在很多計(jì)算機(jī)書籍中，它們也通常作為高階函數(shù)來介紹。而我自己在日常工作中，經(jīng)常使用它們來使代碼更快，更易于理解。

Lambda 函數(shù)

Lambda函數(shù)用于創(chuàng)建匿名函數(shù)，即沒有名稱的函數(shù)。它只是一個(gè)表達(dá)式，函數(shù)體比def簡(jiǎn)單很多。當(dāng)我們需要?jiǎng)?chuàng)建一個(gè)函數(shù)來執(zhí)行單個(gè)操作并且可以在一行中編寫時(shí)，就可以用到匿名函數(shù)了。

lambda?[arg1?[,arg2,.....argn]]:expression

lambda的主體是一個(gè)表達(dá)式，而不是一個(gè)代碼塊。僅僅能在lambda表達(dá)式中封裝有限的邏輯進(jìn)去。例如：

lambda?x:?x+2

如果我們也想像def定義的函數(shù)隨時(shí)調(diào)用，可以將lambda函數(shù)分配給這樣的函數(shù)對(duì)象。

add2?=?lambda?x:?x+2
add2(10)

輸出結(jié)果：

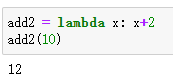
利用Lambda函數(shù)，可以將代碼簡(jiǎn)化很多，具體再舉個(gè)例子。

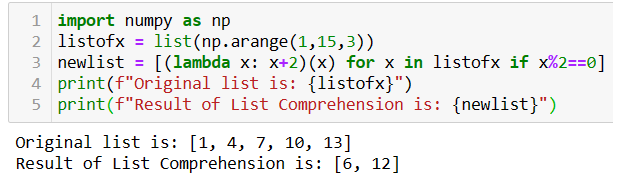
如上圖所示，結(jié)果列表newlist是使用lambda函數(shù)用一行代碼生成的。

Map 函數(shù)

map()函數(shù)會(huì)將一個(gè)函數(shù)映射到一個(gè)輸入列表的所有元素上。

map(function,iterable)

比如我們先創(chuàng)建了一個(gè)函數(shù)來返回一個(gè)大寫的輸入單詞，然后將此函數(shù)應(yīng)有到列表colors中的所有元素。

def?makeupper(word):
????return?word.upper()

colors=['red','yellow','green','black']
colors_uppercase=list(map(makeupper,colors))
colors_uppercase

輸出結(jié)果：

此外，我們還可以使用匿名函數(shù)lambda來配合map函數(shù)，這樣可以更加精簡(jiǎn)。

colors=['red','yellow','green','black']
colors_uppercase=list(map(lambda?x:?x.upper(),colors))
colors_uppercase

如果我們不用Map函數(shù)的話，就需要使用for循環(huán)。

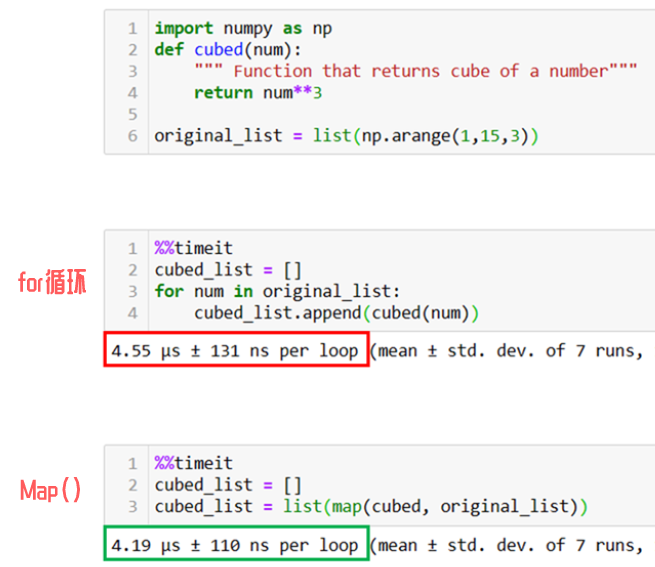
如上圖所示，在實(shí)際使用中Map函數(shù)會(huì)比f(wàn)or循環(huán)依次列表元素的方法快1.5倍。

Reduce函數(shù)

當(dāng)需要對(duì)一個(gè)列表進(jìn)行一些計(jì)算并返回結(jié)果時(shí)，reduce()是個(gè)非常有用的函數(shù)。舉個(gè)例子，當(dāng)需要計(jì)算一個(gè)整數(shù)列表所有元素的乘積時(shí)，即可使用reduce函數(shù)實(shí)現(xiàn)。^[1]

它與函數(shù)的最大的區(qū)別就是，reduce()里的映射函數(shù)（function）接收兩個(gè)參數(shù)，而map接收一個(gè)參數(shù)。

reduce(function,?iterable[,?initializer])?

接下來我們用實(shí)例來演示reduce()的代碼執(zhí)行過程。

from?functools?import?reduce
def?add(x,?y)?:???#?兩數(shù)相加
????return?x?+?y
numbers?=?[1,2,3,4,5]
sum1?=?reduce(add,?numbers)???#?計(jì)算列表和

得到結(jié)果sum1 = 15，其代碼執(zhí)行過程如下方動(dòng)圖所示。

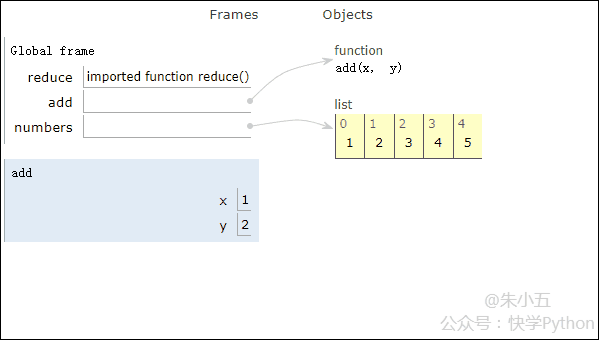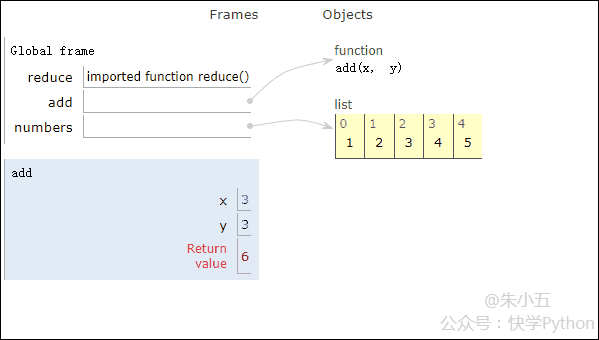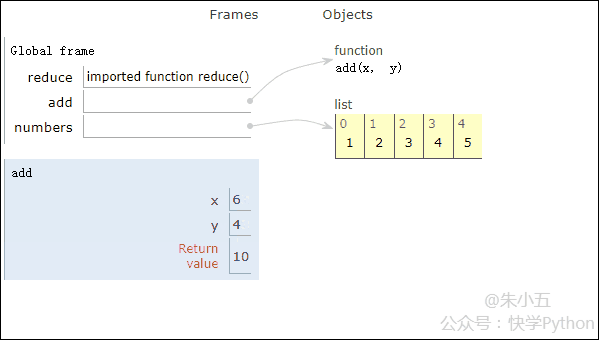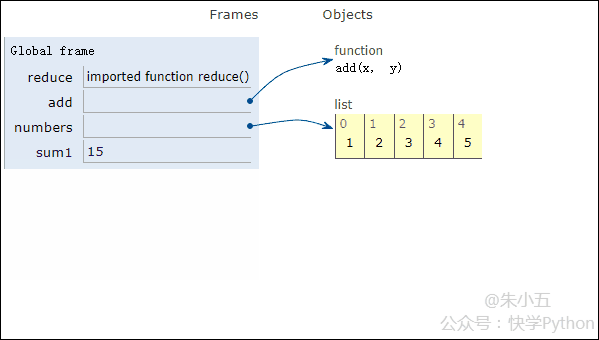
結(jié)合上圖我們會(huì)看到，reduce將一個(gè)相加函數(shù)add()作用在一個(gè)列表[1,2,3,4,5]上，映射函數(shù)接收了兩個(gè)參數(shù)，reduce()把結(jié)果繼續(xù)和列表的下一個(gè)元素做累加計(jì)算。

此外，我們同樣可以使用匿名函數(shù)lambda來配合reduce函數(shù)，這樣可以更加精簡(jiǎn)。

from?functools?import?reduce
numbers?=?[1,2,3,4,5]
sum2?=?reduce(lambda?x,?y:?x+y,?numbers)

得到輸出sum2= 15，與之前結(jié)果保持一致。

需要注意：Python3.x開始reduce()已經(jīng)被移到functools模塊里^[2]，如果我們要使用，需要用from functools import reduce導(dǎo)入.

enumerate 函數(shù)

enumerate()函數(shù)用于將一個(gè)可遍歷的數(shù)據(jù)對(duì)象(如列表、元組或字符串)組合為一個(gè)索引序列，同時(shí)列出數(shù)據(jù)和數(shù)據(jù)下標(biāo)，一般用在for循環(huán)當(dāng)中。它的語(yǔ)法如下所示：

enumerate(iterable,?start=0)

它的兩個(gè)參數(shù)，一個(gè)是序列、迭代器或其他支持迭代對(duì)象；另一個(gè)是下標(biāo)起始位置，默認(rèn)情況從0開始，也可以自定義計(jì)數(shù)器的起始編號(hào)。

colors?=?['red',?'yellow',?'green',?'black']
result?=?enumerate(colors)

如果我們有一個(gè)存放colors的顏色列表，運(yùn)行后就會(huì)得到一個(gè)enumerate(枚舉) 對(duì)象。它可以直接在for循環(huán)中使用，也可以轉(zhuǎn)換為列表，具體用法如下所示。

for?count,?element?in?result:
????print(f"迭代編號(hào):{count},對(duì)應(yīng)元素:{element}")

Zip 函數(shù)

zip()函數(shù)用于將可迭代的對(duì)象作為參數(shù)，將對(duì)象中對(duì)應(yīng)的元素打包成一個(gè)個(gè)元組，然后返回由這些元組組成的列表^[3]。

我們還是用兩個(gè)列表作為例子演示：

colors?=?['red',?'yellow',?'green',?'black']
fruits?=?['apple',?'pineapple',?'grapes',?'cherry']
for?item?in?zip(colors,fruits):
????print(item)

輸出結(jié)果：

當(dāng)我們使用zip()函數(shù)時(shí)，如果各個(gè)迭代器的元素個(gè)數(shù)不一致，則返回列表長(zhǎng)度與最短的對(duì)象相同。

prices?=[100,50,120]
for?item?in?zip(colors,fruits,prices):
????print(item)

Filter 函數(shù)

filter()函數(shù)用于過濾序列，過濾掉不符合條件的元素，返回由符合條件元素組成的新列表，其語(yǔ)法如下所示^[4]。

filter(function,?iterable)

比如舉個(gè)例子，我們可以先創(chuàng)建一個(gè)函數(shù)來檢查單詞是否為大寫，然后使用filter()函數(shù)過濾出列表中的所有奇數(shù)：

def?is_odd(n):
????return?n?%?2?==?1

old_list?=?[1,?2,?3,?4,?5,?6,?7,?8,?9,?10]

new_list?=?filter(is_odd,?old_list)
print(newlist)

輸出結(jié)果：

今天分享的這6個(gè)內(nèi)置函數(shù)，在使用 Python 進(jìn)行數(shù)據(jù)分析或者其他復(fù)雜的自動(dòng)化任務(wù)時(shí)非常方便。

如果喜歡本文，歡迎給右下角點(diǎn)贊??

參考資料