Go 數(shù)據(jù)結(jié)構(gòu)和算法篇（十五）：二叉樹(shù)的定義和存儲(chǔ)

一、樹(shù)的相關(guān)概念

樹(shù)這種數(shù)據(jù)結(jié)構(gòu)模擬了自然界中樹(shù)的概念，自然界中的樹(shù)有根、葉子、枝干，數(shù)據(jù)結(jié)構(gòu)中的樹(shù)也是如此，只不過(guò)是倒過(guò)來(lái)的：

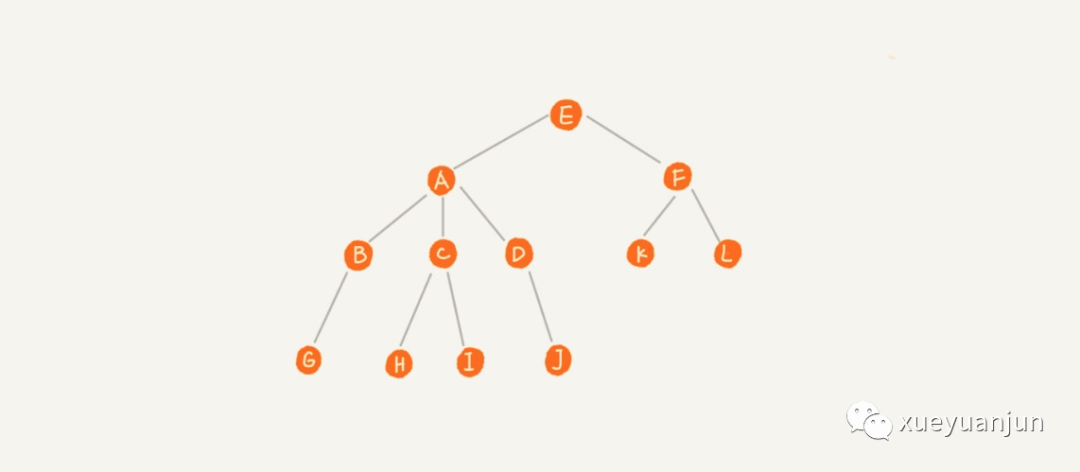
其中的每個(gè)元素叫做節(jié)點(diǎn)。樹(shù)的頂點(diǎn)（沒(méi)有父元素的節(jié)點(diǎn)）叫根節(jié)點(diǎn)，如 E；每個(gè)分支的末端節(jié)點(diǎn)（沒(méi)有子元素的節(jié)點(diǎn)）叫葉子節(jié)點(diǎn)，如 G、H、I、J、K、L；用來(lái)連接相鄰節(jié)點(diǎn)之間的關(guān)系叫父子關(guān)系，比如 E 是 A、F 的父節(jié)點(diǎn)，A、F 是 E 的子節(jié)點(diǎn)；具有同一個(gè)父節(jié)點(diǎn)的多個(gè)子節(jié)點(diǎn)叫做兄弟節(jié)點(diǎn)，比如 A、F 是兄弟節(jié)點(diǎn)。

節(jié)點(diǎn)擁有的子節(jié)點(diǎn)數(shù)目叫做節(jié)點(diǎn)的度，顯然，葉子節(jié)點(diǎn)的度為 0，樹(shù)的度是樹(shù)內(nèi)各節(jié)點(diǎn)度的最大值。

除此之外，樹(shù)還有高度、深度和層的概念：

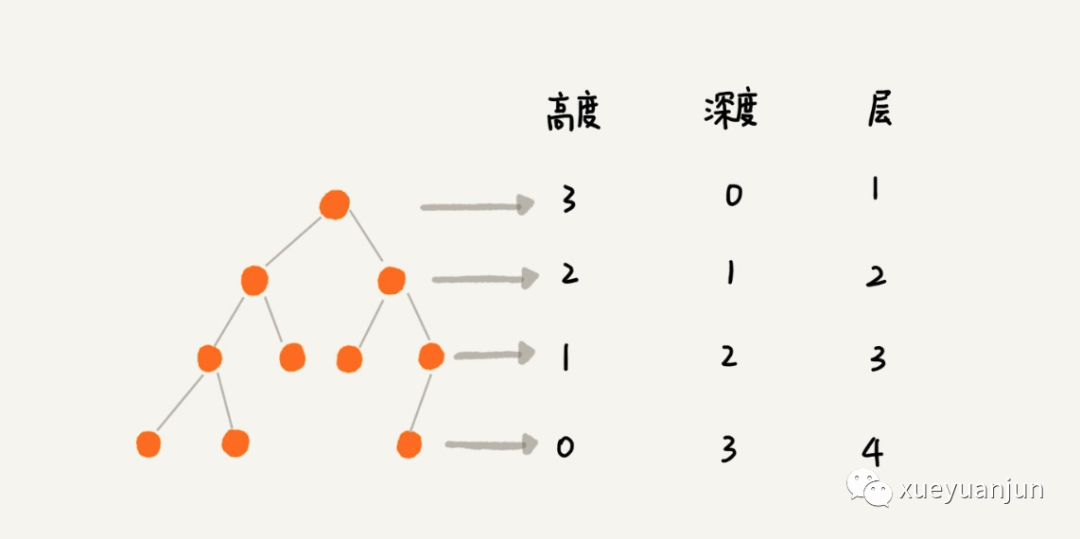
注：其實(shí)線性表也可以看作一種特殊的樹(shù)，只不過(guò)所有節(jié)點(diǎn)都在一個(gè)分支上，第一個(gè)元素是根節(jié)點(diǎn)，最后一個(gè)元素是子節(jié)點(diǎn)，沒(méi)有兄弟節(jié)點(diǎn)。層數(shù)就是線性表的長(zhǎng)度。

多個(gè)互不相交的樹(shù)可以構(gòu)成森林。

二、二叉樹(shù)的定義

二叉樹(shù)是我們平時(shí)遇到的最常見(jiàn)的樹(shù)結(jié)構(gòu)，它是一種特殊的樹(shù)，顧名思義，就是每個(gè)節(jié)點(diǎn)最多有兩個(gè)「分叉」，即兩個(gè)子節(jié)點(diǎn)，分別是左子節(jié)點(diǎn)和右子節(jié)點(diǎn)，不過(guò)，二叉樹(shù)并不要求每個(gè)節(jié)點(diǎn)都有兩個(gè)子節(jié)點(diǎn)，有的節(jié)點(diǎn)只有左子節(jié)點(diǎn)，有的節(jié)點(diǎn)只有右子節(jié)點(diǎn)。比如下面這些都是二叉樹(shù)：

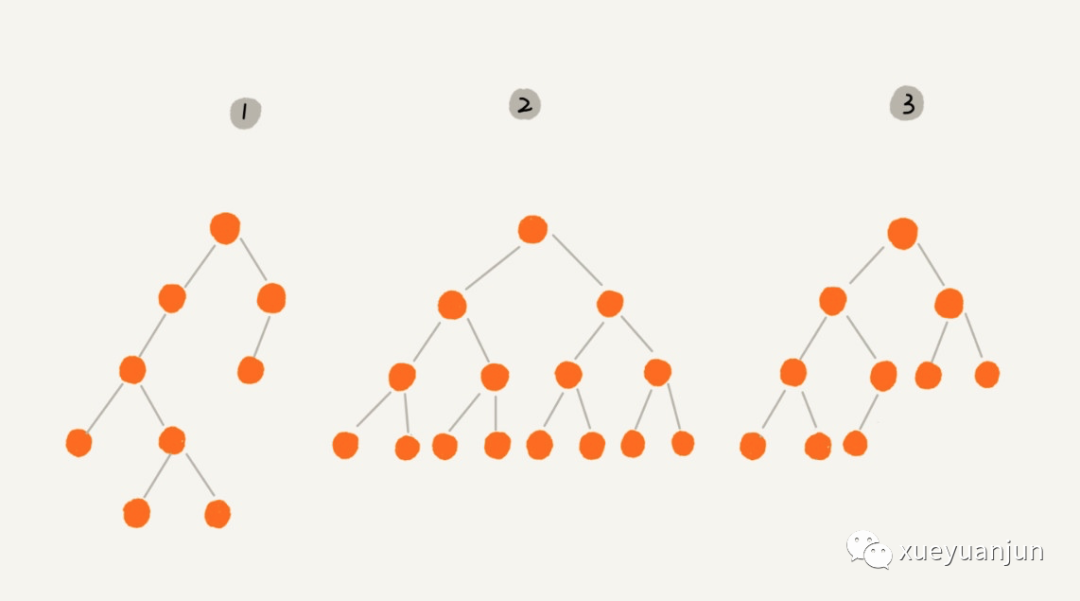
根據(jù)左右子節(jié)點(diǎn)的飽和度，我們又從二叉樹(shù)中提取出兩種特殊的二叉樹(shù) —— 滿二叉樹(shù)和完全二叉樹(shù)。滿二叉樹(shù)即所有分支節(jié)點(diǎn)都有左右子節(jié)點(diǎn)，并且所有葉子節(jié)點(diǎn)都在同一層上，如上面的圖2便是滿二叉樹(shù)。完全二叉樹(shù)要復(fù)雜一些，深度為 k 有 n 個(gè)節(jié)點(diǎn)的二叉樹(shù)，當(dāng)且僅當(dāng)其中的每一節(jié)點(diǎn)，都可以和同樣深度 k 的滿二叉樹(shù)，序號(hào)為 1 到 n 的節(jié)點(diǎn)一對(duì)一對(duì)應(yīng)時(shí)，稱為完全二叉樹(shù)，比如上面的圖3就是完全二叉樹(shù)。

三、二叉樹(shù)的特性

在討論二叉樹(shù)的創(chuàng)建和存儲(chǔ)之前，我們先來(lái)總結(jié)下二叉樹(shù)的一些特性，以便后續(xù)用到（這里二叉樹(shù)數(shù)的深度定義采用的最大層次數(shù)，如果從 0 開(kāi)始計(jì)算的話，可以自行推演一下）：

性質(zhì)1：

在第 i 層最多有 2^i-1 個(gè)節(jié)點(diǎn)。

性質(zhì)2：

深度為 k 的二叉樹(shù)最多有 2^k-1 個(gè)節(jié)點(diǎn)。

性質(zhì)3：

對(duì)于任何一個(gè)二叉樹(shù)，葉子節(jié)點(diǎn)數(shù)為 n₀，度為 2 的節(jié)點(diǎn)數(shù)為 n₂，則 n₀ = n₂+1。

性質(zhì)4：

性質(zhì)5：

樹(shù)這種結(jié)構(gòu)不能簡(jiǎn)單通過(guò)線性表的前后關(guān)系來(lái)存儲(chǔ)，在線性表中，一個(gè)節(jié)點(diǎn)只有至多一個(gè)前驅(qū)節(jié)點(diǎn)和至多一個(gè)后驅(qū)節(jié)點(diǎn)，樹(shù)則不然，一個(gè)節(jié)點(diǎn)可能有多個(gè)后驅(qū)節(jié)點(diǎn)，這個(gè)時(shí)候，我們需要通過(guò)更加復(fù)雜的結(jié)構(gòu)才能存儲(chǔ)樹(shù)。

二叉樹(shù)是一種特殊的樹(shù)，比多叉樹(shù)要簡(jiǎn)單，因?yàn)樘囟ü?jié)點(diǎn)至多只有兩個(gè)節(jié)點(diǎn)，這就極大簡(jiǎn)化了相應(yīng)的數(shù)據(jù)結(jié)構(gòu)，使得通過(guò)線性表就可以實(shí)現(xiàn)二叉樹(shù)的存儲(chǔ)。我們后面基本只討論二叉樹(shù)，下面我們通過(guò)數(shù)組和鏈表來(lái)演示如何存儲(chǔ)二叉樹(shù)。

四、通過(guò)數(shù)組存儲(chǔ)二叉樹(shù)

對(duì)于特定的二叉樹(shù)而言，比如滿二叉樹(shù)、完全二叉樹(shù)，它們的節(jié)點(diǎn)之間是有一定關(guān)聯(lián)關(guān)系的，以下面這棵完全二叉樹(shù)為例：

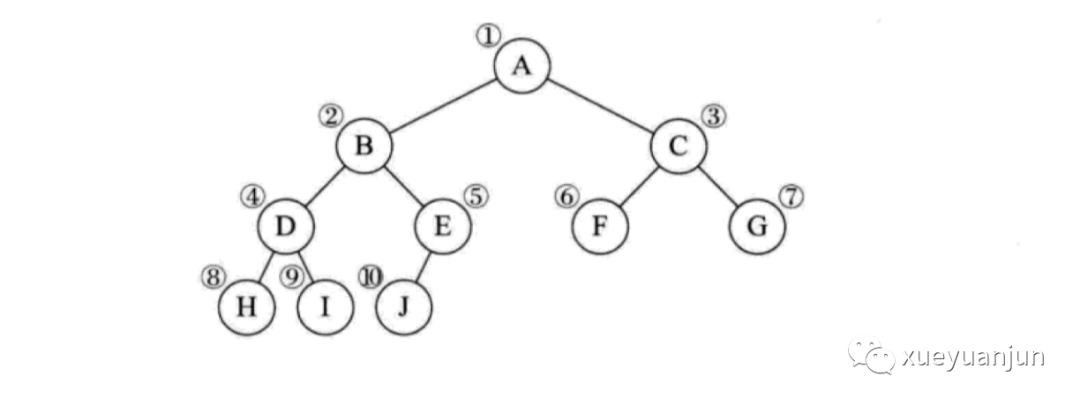
我們按照從上到下，從左到右對(duì)所有節(jié)點(diǎn)編號(hào)，可以看到，下一層的左右子節(jié)點(diǎn)和對(duì)應(yīng)父節(jié)點(diǎn)序號(hào)存在某種數(shù)學(xué)關(guān)系，如果父節(jié)點(diǎn)的序號(hào)是 i，其對(duì)應(yīng)左子節(jié)點(diǎn)位于 2i 的位置上，對(duì)應(yīng)右子節(jié)點(diǎn)位于 2i + 1 的位置上，我們可以參照這個(gè)規(guī)則將上述完全二叉樹(shù)存儲(chǔ)到數(shù)組中：

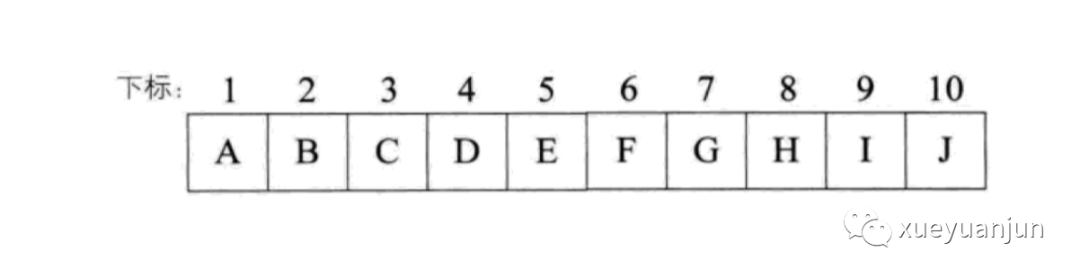
注意我們的下標(biāo)從 1 開(kāi)始（根節(jié)點(diǎn)），索引為 0 的下標(biāo)舍棄，浪費(fèi)這個(gè)空間，以方便計(jì)算。這樣，我們就可以從根節(jié)點(diǎn)開(kāi)始，依次將所有節(jié)點(diǎn)元素存放到數(shù)組中，并且可以根據(jù)節(jié)點(diǎn)間的數(shù)學(xué)關(guān)系很方便地遍歷整棵樹(shù)。此外，由于完全二叉樹(shù)的特殊性，除了第一個(gè)元素之外，該數(shù)組不存在任何空間的浪費(fèi)。由于滿二叉樹(shù)是完全二叉樹(shù)的子集，所以也可以通過(guò)這種方式來(lái)存儲(chǔ)。

那么其它二叉樹(shù)呢？當(dāng)然也可以按照這種思路來(lái)做，我們把不存在的節(jié)點(diǎn)補(bǔ)全，比如假設(shè)上述序號(hào)為 4、6、8、9 的元素不存在：

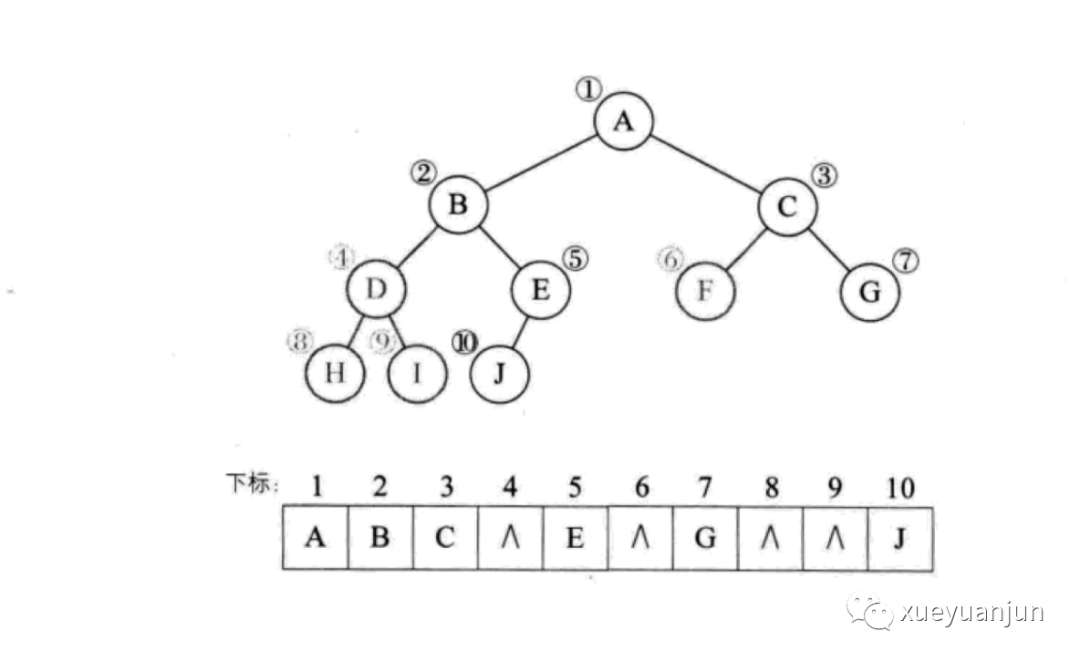
可以看到，我們將不存在的元素補(bǔ)上，只是對(duì)應(yīng)位置值為 null，缺失的節(jié)點(diǎn)越多，數(shù)組的「空洞」也就越多，如果是極端情況，比如二叉樹(shù)只包含 1、3、7 三個(gè)元素，那么數(shù)組中將會(huì)存在大量的「空洞」，浪費(fèi)大量的空間，而且也會(huì)影響性能。

綜上，數(shù)組適合滿二叉樹(shù)、完全二叉樹(shù)這些特殊二叉樹(shù)的存儲(chǔ)，一些比較稠密的二叉樹(shù)也可以用數(shù)組，如果二叉樹(shù)比較稀疏就不適合用數(shù)組了，我們可以通過(guò)鏈表來(lái)存儲(chǔ)它們。

五、通過(guò)鏈表存儲(chǔ)二叉樹(shù)

理論上來(lái)說(shuō)，鏈表適用于所有的二叉樹(shù)存儲(chǔ)，只不過(guò)這里我們需要對(duì)線性表中的鏈表進(jìn)行擴(kuò)展，因?yàn)槎鏄?shù)特定節(jié)點(diǎn)最多有兩個(gè)子節(jié)點(diǎn)，所有我們?cè)阪湵斫Y(jié)點(diǎn)上設(shè)置兩個(gè)指針域，分別指向左右子節(jié)點(diǎn)，所以這種鏈表結(jié)構(gòu)又被稱作二叉鏈表。我們可以通過(guò)一個(gè)結(jié)構(gòu)體表示二叉鏈表的節(jié)點(diǎn)：

// 節(jié)點(diǎn)類type Node struct {    Value string    Left *Node    Right *Node}
// 初始化根節(jié)點(diǎn)func NewNode(data string) *Node {    return &Node{data, nil, nil}}

如果要用二叉鏈表表示上面的完全二叉樹(shù)，對(duì)應(yīng)的圖示如下：

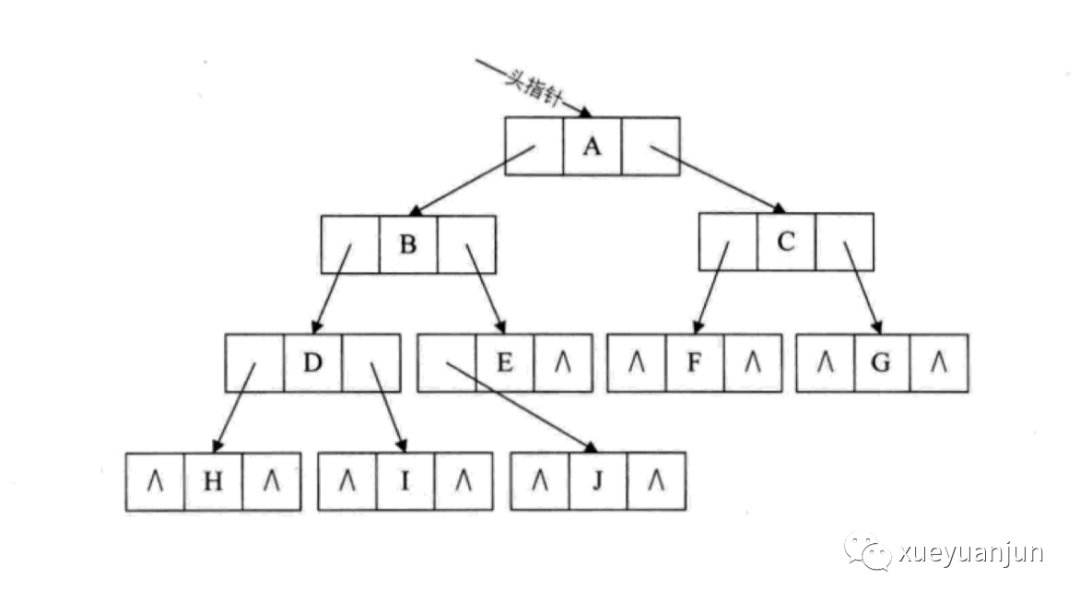
不管是什么樣結(jié)構(gòu)的二叉樹(shù)，用鏈表來(lái)存儲(chǔ)都不會(huì)存在空間的浪費(fèi)。關(guān)于二叉樹(shù)的創(chuàng)建、查找和刪除，需要等到介紹完二叉樹(shù)的遍歷才能開(kāi)始，下一篇我們就來(lái)探討如何遍歷二叉樹(shù)。

（本文完）

推薦閱讀

• Go 數(shù)據(jù)結(jié)構(gòu)和算法篇（十四）：哈希表、哈希函數(shù)、哈希沖突和哈希算法