KNN算法簡(jiǎn)單?我竟用3萬字沒寫清楚······

大家好,我是小伍哥,本文非常長(zhǎng),建議先收藏,有空再看,實(shí)在不行就關(guān)注下我,二維碼放到前面了,我知道大家讀不完,生成了45頁的PDF文檔,關(guān)注我的另一個(gè)號(hào)小伍哥聊風(fēng)控后臺(tái)回復(fù)【KNN】領(lǐng)取。
談起KNN,很多人都會(huì)覺得非常簡(jiǎn)單,甚至?xí)冻霾恍?鄙視,包括我自己,當(dāng)初也是如此,當(dāng)我進(jìn)行深入的研究,發(fā)現(xiàn)真是大意了。
大家都知道KNN可以用于分類,但是它能不能用于回歸?KNN的5個(gè)有監(jiān)督方法你是否都知道?K值怎么確定呢?距離可以加權(quán)么?為了取Top K,必須要對(duì)距離全部排序嗎?基于質(zhì)心的KNN你了解么?有沒有方法減少KNN的計(jì)算復(fù)雜度?KNN還可以做圖發(fā)現(xiàn)?KNN還可以限定鄰居半徑的有監(jiān)督?KNN怎么進(jìn)行異常檢測(cè)?KNN是否能夠找到我想要的鄰居?
在萬物皆顆Embedding的時(shí)代,我們就可以用近鄰?fù)仆扑]Nearest Neighbor(KNN并不低級(jí),Youtube也是用這個(gè),之前還有開源,對(duì)視頻庫中的所有視頻根據(jù)向量做最近鄰算法,得到top-N的視頻作為召回結(jié)果)可以做到:物物推薦,人人推薦,人物推薦。有了文本的Embedding,我們可以進(jìn)行文本聚類挖掘·····,可以說這個(gè)算法非常非常的豐富,加上代碼,30000字,都有很多寫的不是很到位,后面我們慢慢挖。
本文涉及兩個(gè)庫:scikit-learn 和 pyod,前者做有監(jiān)督和距離等計(jì)算,后者負(fù)責(zé)無監(jiān)督,本文的框架也是依據(jù)這兩個(gè)庫展開。
sklearn中KNN相關(guān)類庫:在scikit-learn 中,與近鄰法這一大類相關(guān)的庫都在sklearn.neighbors包之中。KNN分類樹的類是KNeighborsClassifier,KNN回歸樹的類是KNeighborsRegressor。除此之外,還有KNN的擴(kuò)展,即限定半徑最近鄰分類樹的類RadiusNeighborsClassifier和限定半徑最近鄰回歸樹的類RadiusNeighborsRegressor, 以及最近質(zhì)心分類算法NearestCentroid。
在這些算法中,KNN分類和回歸的類參數(shù)完全一樣。限定半徑最近鄰法分類和回歸的類的主要參數(shù)也和KNN基本一樣。
比較特別是的最近質(zhì)心分類算法,由于它是直接選擇最近質(zhì)心來分類,所以僅有兩個(gè)參數(shù),距離度量和特征選擇距離閾值,比較簡(jiǎn)單,因此后面就不再專門講述最近質(zhì)心分類算法的參數(shù)。
另外幾個(gè)在sklearn.neighbors包中但不是做分類回歸預(yù)測(cè)的類也值得關(guān)注,kneighbors_graph類返回用KNN時(shí)和每個(gè)樣本最近的K個(gè)訓(xùn)練集樣本的位置,radius_neighbors_graph返回用限定半徑最近鄰法時(shí)和每個(gè)樣本在限定半徑內(nèi)的訓(xùn)練集樣本的位置。NearestNeighbors是個(gè)大雜燴,它即可以返回用KNN時(shí)和每個(gè)樣本最近的K個(gè)訓(xùn)練集樣本的位置,也可以返回用限定半徑最近鄰法時(shí)和每個(gè)樣本最近的訓(xùn)練集樣本的位置,常常用在聚類模型中,
PyOD中KNN相關(guān)的類庫概述:里面就一個(gè)knn,用于對(duì)異常值的檢測(cè),繼承的是scikit-learn中的NearestNeighbors,所以我們把scikit-learn中的KNN系列理解了,那異常檢測(cè)也就是輕而易舉的拿下了。
一、圖解KNN有監(jiān)督算法當(dāng)KNN用于有監(jiān)督時(shí),可以做分類,也可以回歸,我們這里用分類舉例,也就是喂給該算法模型的數(shù)據(jù)需要帶有類別標(biāo)簽,為了方便算法的理解,我們虛構(gòu)了如下的數(shù)據(jù)集:
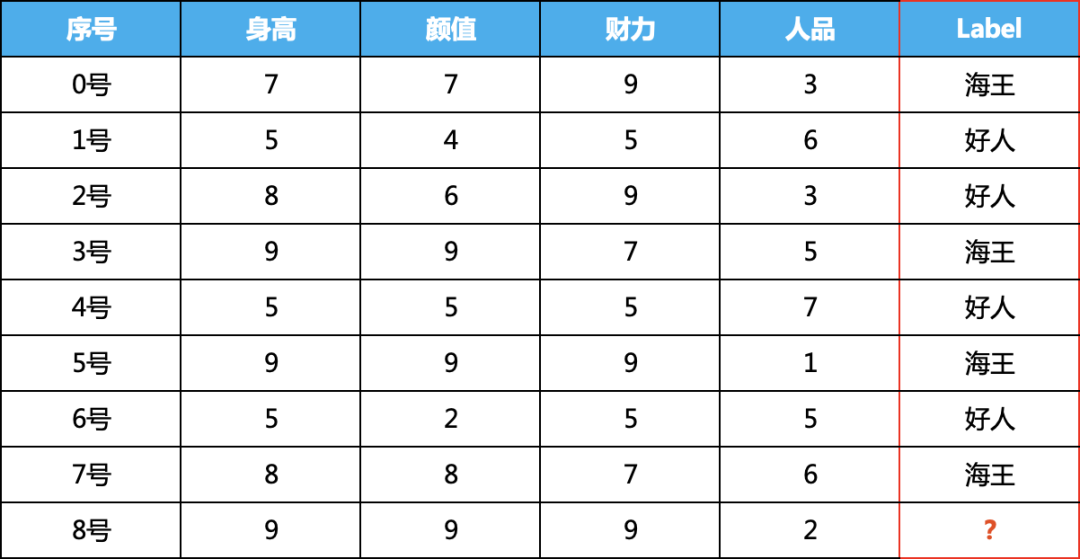
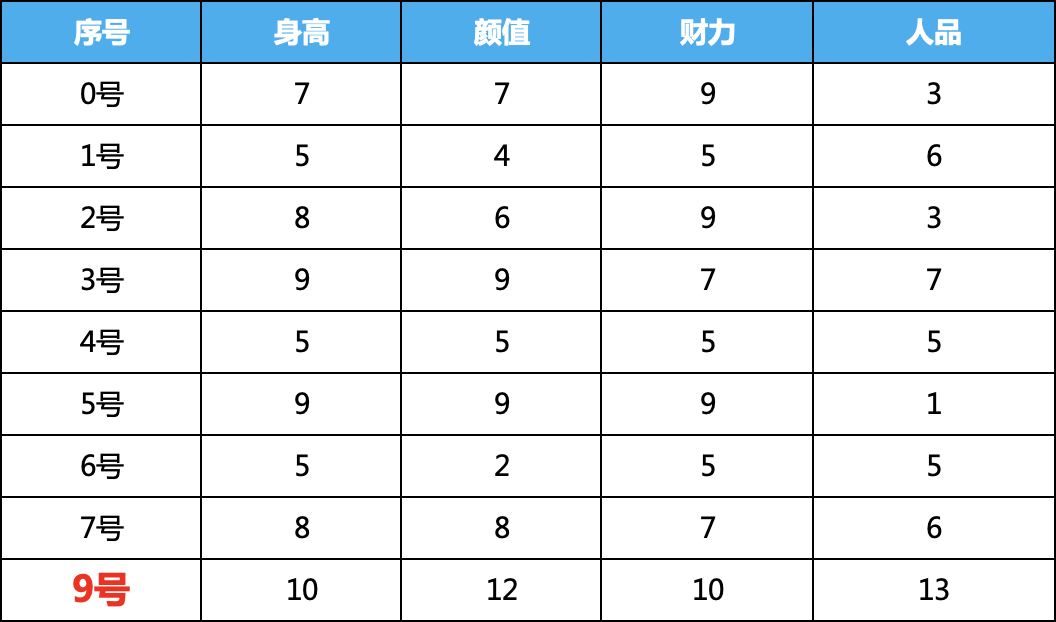
身高、顏值、財(cái)力、人品為數(shù)據(jù)集的特征,最后一列為label,我們需要根據(jù)0-7號(hào)男嘉賓的四個(gè)特征訓(xùn)練模型誰,判斷8號(hào)男嘉賓是好人還是海王。
1、KNN原理
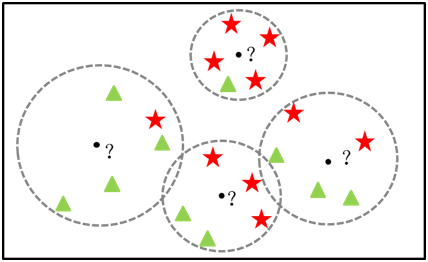
KKN原理:KNN算法非常簡(jiǎn)單粗暴,就是將預(yù)測(cè)點(diǎn)與所有訓(xùn)練集的點(diǎn)進(jìn)行距離計(jì)算,然后保存并排序,選出前面K個(gè)值看看哪個(gè)類別比較多,就將預(yù)測(cè)點(diǎn)歸于哪一類,如下圖,原點(diǎn)為預(yù)測(cè)點(diǎn),最近的三個(gè)樣本,兩個(gè)為紅色三角形,那圓點(diǎn)的類別預(yù)測(cè)紅色三角形類別。
KNN過程:對(duì)未知類別的數(shù)據(jù)集中的每個(gè)點(diǎn)依次執(zhí)行以下操作:
1) 計(jì)算當(dāng)前點(diǎn) 與 已知類別數(shù)據(jù)集中每個(gè)點(diǎn)的距離
2) 按照距離遞增次序排序
3) 選取與當(dāng)前點(diǎn)距離最小的k個(gè)點(diǎn)
4) 確定前k個(gè)點(diǎn)所在類別的出現(xiàn)頻率
5) 返回前k個(gè)點(diǎn)出現(xiàn)比例最高的類別作為當(dāng)前點(diǎn)的預(yù)測(cè)類別
2、KNN實(shí)例講解
這里會(huì)利用上訴的kNN數(shù)據(jù)集對(duì)KNN算法做逐步解釋:
1) 計(jì)算預(yù)測(cè)點(diǎn) 與 已知類別數(shù)據(jù)集中的點(diǎn)之間的距離:
要度量空間中兩個(gè)點(diǎn)的距離,有多種度量方式,常見的有曼哈頓距離、歐式距離等。KNN算法默認(rèn)使用的是歐式距離,計(jì)算方法如下: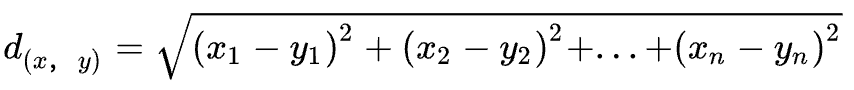 我們計(jì)算8號(hào)與每個(gè)樣本之間的距離,計(jì)算結(jié)果如下:
我們計(jì)算8號(hào)與每個(gè)樣本之間的距離,計(jì)算結(jié)果如下: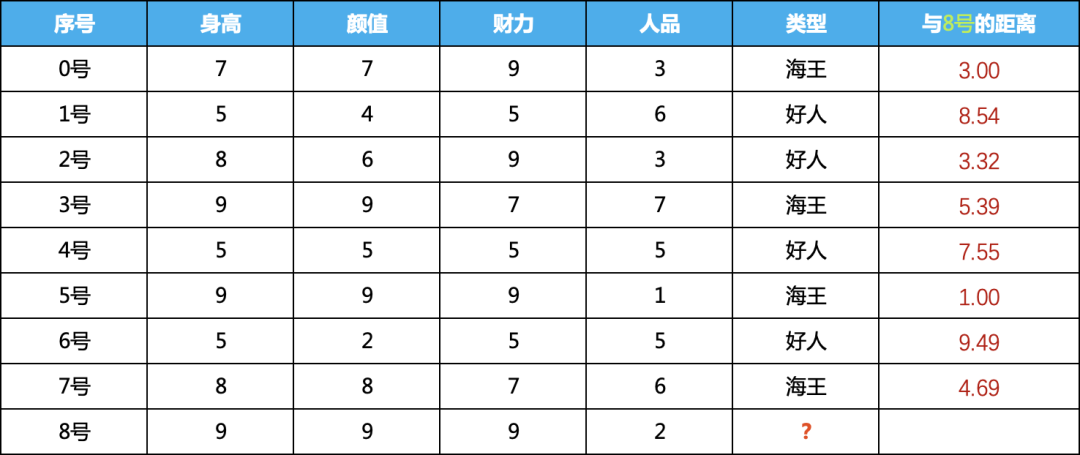
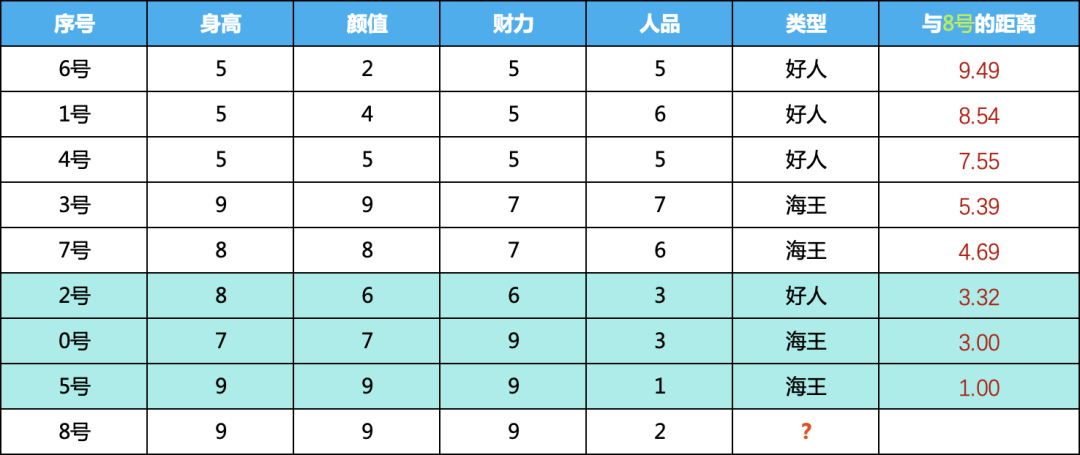
2) 按照計(jì)算的距離降序排列,看看誰與8號(hào)嘉賓的距離最近
按照與8號(hào)的距離排序,如下,可以看到,5號(hào),0號(hào),2號(hào)三個(gè)排的最近
3) 選取與預(yù)測(cè)點(diǎn)距離最小的k個(gè)點(diǎn)
我們知道K的取值比較重要,那么一般如何確定K的取值呢?答案是通過交叉驗(yàn)證,從選取一個(gè)較小的K值開始,不斷增加K的值,然后計(jì)算驗(yàn)證集合的準(zhǔn)確率,最終找到一個(gè)比較合適的K值。我們這里取3和5分別看看預(yù)測(cè)的結(jié)果,大家對(duì)取不同的K值有個(gè)直觀的感受。
K = 3

K = 5
4) 確定最近的k個(gè)鄰居所在類別的頻率
當(dāng) k = 3 的時(shí)候,包含2個(gè)海王和1個(gè)好人
好人的概率:1/3 = 0.3333
海王的概率:2/3 = 0.6666
當(dāng) k =5 的時(shí)候,包含4個(gè)海王和1個(gè)好人
好人的概率:1/5 = 0.2000
海王的概率:4/5 = 0.8000
由此可以看出來,k大小會(huì)影響我們對(duì)概率的判斷,在本例中,不影響判斷的類別,但是影響概率
5) 返回前k個(gè)點(diǎn)出現(xiàn)頻率最高的類別作為當(dāng)前點(diǎn)的預(yù)測(cè)分類
無論是k取3還是5,都是海王的概率大于好人的概率,因此我們對(duì)8號(hào)嘉賓的預(yù)測(cè)時(shí)海王,當(dāng)然,最后的概率也可以輸出是0.6666或者0.8.由此也可以看到,K值會(huì)比較大的影響預(yù)測(cè)結(jié)果
6)利用sklearn進(jìn)行檢驗(yàn)
我們手動(dòng)算了上面的數(shù)據(jù),現(xiàn)在用sklearn的算法檢驗(yàn)我們的計(jì)算結(jié)果,看看有沒有算對(duì) ? ? ?
# 構(gòu)建數(shù)據(jù)集,按上面的表格
X = np.array([[7, 7, 9, 3],
[5, 4, 5, 6],
[8, 6, 9, 3],
[9, 9, 7, 7],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 8, 7, 6]])
# 訓(xùn)練Label準(zhǔn)備,1-海王,0-好人
y = [1, 0, 0, 1,0,1,0,1]
# 加載分類模型 k = 3
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X, y)
# 預(yù)測(cè)8號(hào)嘉賓 [[9, 9, 9, 2]] 的類別和概率
print(neigh.predict([[9, 9, 9, 2]]))
[1]
print(neigh.predict_proba([[9, 9, 9, 2]]))
[[0.33333333 0.66666667]]
# 加載分類模型 k = 5
neigh = KNeighborsClassifier(n_neighbors=5)
neigh.fit(X, y)
# 預(yù)測(cè)8號(hào)嘉賓 [[9, 9, 9, 2]] 的類別和概率
print(neigh.predict([[9, 9, 9, 2]]))
[1]
print(neigh.predict_proba([[9, 9, 9, 2]]))
[[0.2 0.8]]
簡(jiǎn)直完美,和我們手動(dòng)計(jì)算的一模一樣,到此,我們就算理解了基礎(chǔ)的KNN算法,當(dāng)然,應(yīng)用的時(shí)候,涉及到更多的數(shù)據(jù)處理以及更多的參數(shù),我們?cè)谙旅尜N出來。我們上面用分類任務(wù)舉例,其實(shí)對(duì)于回歸任務(wù),我們只要找到最近的鄰居,然后按鄰居的取值取平均值或者中位數(shù)就可以了。
二、KNN有監(jiān)督算法應(yīng)用KNN用于有監(jiān)督算法主要有五個(gè),分類的類是KNeighborsClassifier,回歸的類是KNeighborsRegressor,除此之外,還有KNN的擴(kuò)展,即限定半徑最近鄰分類的類RadiusNeighborsClassifier和限定半徑最近鄰回歸樹的類RadiusNeighborsRegressor, 以及最近質(zhì)心分類算法NearestCentroid。我們下面看看這個(gè)五個(gè)算法的基本用法和案例。
1、KNeighborsClassifier
1)基本用法
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
2)參數(shù)詳解
n_neighbors: ?默認(rèn)為5, ?就是k-NN的k的值, ?選取最近的k個(gè)點(diǎn)
weights: ?默認(rèn)是uniform, ?參數(shù)可以是uniform、distance, ?也可以是用戶自己定義的函數(shù)
uniform: ?是均等的權(quán)重, ?就說所有的鄰近點(diǎn)的權(quán)重都是相等的
distance: ?是不均等的權(quán)重, ?距離近的點(diǎn)比距離遠(yuǎn)的點(diǎn)的影響大
用戶自定義的函數(shù), ?接收距離的數(shù)組, ?返回一組維數(shù)相同的權(quán)重
algorithm: ?快速k近鄰搜索算法, ?默認(rèn)參數(shù)為auto, ?可以理解為算法自己決定合適的搜索算法. ?除此之外, ?用戶也可以自己指定搜索算法: ?ball_tree、kd_tree、brute方法進(jìn)行搜索.
kd_tree: ?構(gòu)造kd樹存儲(chǔ)數(shù)據(jù)以便對(duì)其進(jìn)行快速檢索的樹形數(shù)據(jù)結(jié)構(gòu). ?kd樹也就是數(shù)據(jù)結(jié)構(gòu)中的二叉樹. 以中值切分構(gòu)造的樹, ?每個(gè)結(jié)點(diǎn)是一個(gè)超矩形, ?在維數(shù)小于20時(shí)效率高
ball_tree: ?是為了克服kd樹高緯失效而發(fā)明的,其構(gòu)造過程是以質(zhì)心 C 和半徑 r 分割樣本空間, ?每個(gè)節(jié)點(diǎn)是一個(gè)超球體
brute: ?是蠻力搜索, ?也就是線性掃描, ?當(dāng)訓(xùn)練集很大時(shí), ?計(jì)算非常耗時(shí)
leaf_size: 默認(rèn)是30, ?這個(gè)是構(gòu)造的kd樹和ball樹的大小. ?這個(gè)值的設(shè)置會(huì)影響樹構(gòu)建的速度和搜索速度, ?同樣也影響著存儲(chǔ)樹所需的內(nèi)存大小. ?需要根據(jù)問題的性質(zhì)選擇最優(yōu)的大小
p: ? minkowski距離度量里的參數(shù). p=2時(shí)是歐氏距離, p=1時(shí)是曼哈頓距離,對(duì)于任意p, 就是minkowski距離
metric: ?用于距離度量, ?默認(rèn)的度量是minkowski距離 (也就是L_p距離), ?當(dāng)p=2時(shí)就是歐氏距離
metric_params: ?距離公式的其他關(guān)鍵參數(shù). 默認(rèn)為None
n_jobs: ?并行處理的個(gè)數(shù). 默認(rèn)為1. ?如果為-1, 那么那么CPU的所有cores都用于并行工作
3)Attributes-屬性
effective_metric_:模型計(jì)算距離是用的距離類型
effective_metric_params_:模型計(jì)算距離是用的距離類型
n_features_in_:訓(xùn)練集用的特征數(shù)量
feature_names_in_:特征名稱
n_samples_fit_:訓(xùn)練集中的樣本數(shù)
4)Methods-方法
fit(X, y) | 使用X作為訓(xùn)練數(shù)據(jù),y作為目標(biāo)值(類似于標(biāo)簽)來擬合模型。 |
get_params([deep]) | 獲取估值器的參數(shù)。 |
kneighbors([X, n_neighbors, return_distance]) | 查找一個(gè)或幾個(gè)點(diǎn)的K個(gè)鄰居。 |
kneighbors_graph([X, n_neighbors, mode]) | 計(jì)算在X數(shù)組中每個(gè)點(diǎn)的k鄰居的(權(quán)重)圖。 |
predict(X) | 給提供的數(shù)據(jù)預(yù)測(cè)對(duì)應(yīng)的標(biāo)簽。 |
predict_proba(X) | 返回測(cè)試數(shù)據(jù)X的概率估值。 |
score(X, y[, sample_weight]) | 返回給定測(cè)試數(shù)據(jù)和標(biāo)簽的平均準(zhǔn)確值。 |
set_params(**params) | 設(shè)置估值器的參數(shù) |
2、KNeighborsRegressor
1)基本用法
sklearn.neighbors.KNeighborsRegressor(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
2)參數(shù)詳解
通上,KNeighborsClassifier,回歸的參數(shù)和分類的參數(shù)一模一樣,無須贅述,看上面的數(shù)據(jù)就行。
3)案例分析
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsRegressor
neigh = KNeighborsRegressor(n_neighbors=2)
neigh.fit(X, y)
KNeighborsRegressor(n_neighbors=2)
print(neigh.predict([[1.5]]))
[0.5]
3、RadiusNeighborsClassifier
除了上面KNeighborsClassifier 和 KNeighborsRegressor,與之對(duì)應(yīng)的還有RadiusNeighborsClassifier 和 RadiusNeighborsRegressor,那么他們之間有什么區(qū)別呢?一個(gè)是靠半徑來確定最近鄰居,確定半徑,有多少算多少,通過半徑內(nèi)的鄰居確定預(yù)測(cè)數(shù)據(jù)的類別或者回歸值,一個(gè)是靠K值來確定鄰居,K幾個(gè)就取幾個(gè),不管跨度有多大,就是要找到K個(gè)才罷休,然后根據(jù)找到的K個(gè)計(jì)算預(yù)測(cè)數(shù)據(jù)的類別或者回歸值,具體用法和參數(shù)我們看下面的介紹。
1)基本用法
sklearn.neighbors.RadiusNeighborsClassifier(radius=1.0, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', outlier_label=None, metric_params=None, n_jobs=None, **kwargs)
2)參數(shù)注釋
radius:尋找最鄰近數(shù)據(jù)點(diǎn)的半徑,半徑的選擇與樣本分布有關(guān),可以通過交叉驗(yàn)證來選擇一個(gè)較小的半徑,盡量保證每類訓(xùn)練樣本其他類別樣本的距離較遠(yuǎn),默認(rèn)值是1.0。如果數(shù)據(jù)是三維或者三維以下的,可以通過可視化觀察來調(diào)參。
weights: ?默認(rèn)是uniform, ?參數(shù)可以是uniform、distance, ?也可以是用戶自己定義的函數(shù)
uniform: ?是均等的權(quán)重, ?就說所有的鄰近點(diǎn)的權(quán)重都是相等的
distance: ?是不均等的權(quán)重, ?距離近的點(diǎn)比距離遠(yuǎn)的點(diǎn)的影響大
自定義:用戶自定義的函數(shù), ?接收距離的數(shù)組, ?返回一組維數(shù)相同的權(quán)重
選擇默認(rèn)的"uniform",意味著所有最近鄰樣本權(quán)重都一樣,在做預(yù)測(cè)時(shí)一視同仁。如果是"distance",則權(quán)重和距離成反比例,即距離預(yù)測(cè)目標(biāo)更近的近鄰具有更高的權(quán)重,這樣在預(yù)測(cè)類別或者做回歸時(shí),更近的近鄰所占的影響因子會(huì)更加大。當(dāng)然,我們也可以自定義權(quán)重,即自定義一個(gè)函數(shù),輸入是距離值,輸出是權(quán)重值。這樣我們可以自己控制不同的距離所對(duì)應(yīng)的權(quán)重。一般來說,如果樣本的分布是比較成簇的,即各類樣本都在相對(duì)分開的簇中時(shí),我們用默認(rèn)的"uniform"就可以了,如果樣本的分布比較亂,規(guī)律不好尋找,選擇"distance"是一個(gè)比較好的選擇。如果用"distance"發(fā)現(xiàn)預(yù)測(cè)的效果的還是不好,可以考慮自定義距離權(quán)重來調(diào)優(yōu)這個(gè)參數(shù)。
algorithm: ?快速k近鄰搜索算法, ?默認(rèn)參數(shù)為auto, ?可以理解為算法自己決定合適的搜索算法. ?除此之外, ?用戶也可以自己指定搜索算法: ?ball_tree、kd_tree、brute方法進(jìn)行搜索。
kd_tree: ?構(gòu)造kd樹存儲(chǔ)數(shù)據(jù)以便對(duì)其進(jìn)行快速檢索的樹形數(shù)據(jù)結(jié)構(gòu), ?kd樹也就是數(shù)據(jù)結(jié)構(gòu)中的二叉樹. 以中值切分構(gòu)造的樹, ?每個(gè)結(jié)點(diǎn)是一個(gè)超矩形, ?在維數(shù)小于20時(shí)效率高
ball_tree: ?是為了克服kd樹高緯失效而發(fā)明的,其構(gòu)造過程是以質(zhì)心 C 和半徑 r 分割樣本空間, ?每個(gè)節(jié)點(diǎn)是一個(gè)超球體
brute: ?是蠻力搜索, ?也就是線性掃描, ?當(dāng)訓(xùn)練集很大時(shí), ?計(jì)算非常耗時(shí)
leaf_size: 默認(rèn)是30, ?這個(gè)是構(gòu)造的kd樹和ball樹的大小. ?這個(gè)值的設(shè)置會(huì)影響樹構(gòu)建的速度和搜索速度, ?同樣也影響著存儲(chǔ)樹所需的內(nèi)存大小. ?需要根據(jù)問題的性質(zhì)選擇最優(yōu)的大小
outlier_label:主要用于預(yù)測(cè)時(shí),如果目標(biāo)點(diǎn)半徑內(nèi)沒有任何訓(xùn)練集的樣本點(diǎn)時(shí),應(yīng)該標(biāo)記的類別,不建議選擇默認(rèn)值 none,因?yàn)檫@樣遇到異常點(diǎn)會(huì)報(bào)錯(cuò)。一般設(shè)置為訓(xùn)練集里最多樣本的類別。
p: ? minkowski距離度量里的參數(shù). p=2時(shí)是歐氏距離, p=1時(shí)是曼哈頓距離,對(duì)于任意p, 就是minkowski距離
metric: ?用于距離度量, ?默認(rèn)的度量是minkowski距離 (也就是L_p距離), ?當(dāng)p=2時(shí)就是歐氏距離
metric_params: ?距離公式的其他關(guān)鍵參數(shù),默認(rèn)為None
n_jobs: ?并行處理的個(gè)數(shù). 默認(rèn)為1, ?如果為-1, 那么那么CPU的所有cores都用于并行工作
3)屬性詳解
classes_:類別數(shù)量
effective_metric_:使用的距離度量。它將與度量參數(shù)相同或與其相同,例如 如果metric參數(shù)設(shè)置為“ minkowski”,而p參數(shù)設(shè)置為2,則為“ euclidean”。
effective_metric_params_:度量功能的其他關(guān)鍵字參數(shù)。對(duì)于大多數(shù)指標(biāo)而言,它與metric_params參數(shù)相同,但是,如果將valid_metric_屬性設(shè)置為“ minkowski”,則也可能包含p參數(shù)值。
n_features_in_:多少個(gè)特征
feature_names_in_:特征的名稱
n_samples_fit_:訓(xùn)練集的樣本數(shù)
outlier_label_:不在半徑內(nèi)的數(shù)據(jù)怎么處理
outputs_2d_:如果在擬合期間y的形狀為(n_samples,)或(n_samples,1),則為True。
4)方法詳解
fit(X, y) | Fit the radius neighbors classifier from the training dataset. |
get_params([deep]) | Get parameters for this estimator. |
predict(X) | Predict the class labels for the provided data. |
predict_proba(X) | Return probability estimates for the test data X. |
radius_neighbors([X, radius, ...]) | Find the neighbors within a given radius of a point or points. |
radius_neighbors_graph([X, radius, mode, ...]) | Compute the (weighted) graph of Neighbors for points in X. |
score(X, y[, sample_weight]) | Return the mean accuracy on the given test data and labels. |
set_params(**params) | Set the parameters of this estimator. |
5)案例分析
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import RadiusNeighborsClassifier
neigh = RadiusNeighborsClassifier(radius=1.0)
neigh.fit(X, y)
print(neigh.predict([[1.5]]))
[0]
print(neigh.predict_proba([[1.0]]))
[[0.66666667 0.33333333]]
# 我把半徑調(diào)小,就可以看到,找不到鄰居會(huì)報(bào)錯(cuò)
neigh = RadiusNeighborsClassifier(radius=0.1)
neigh.fit(X, y)
print(neigh.predict([[1.5]]))
No neighbors found for test samples array([0], dtype=int64), you can try using larger radius, giving a label for outliers, or considering removing them from your dataset.
# 我們可以設(shè)置下outlier_label這個(gè)參數(shù),然后沒有鄰居的就默認(rèn)一個(gè)類型了
neigh = RadiusNeighborsClassifier(radius=0.1,
outlier_label = 'most_frequent')
neigh.fit(X, y)
print(neigh.predict([[1.5]]))
[0]
print(neigh.predict_proba([[1.0]]))
[[1. 0.]]
neigh.outlier_label_
[0]
# 其他方法
neigh = RadiusNeighborsClassifier(radius=1.0)
neigh.fit(X, y)
neigh.radius_neighbors([[1.3]])
(array([array([0.3, 0.7])], dtype=object),array([array([1, 2], dtype=int64)], dtype=object))
4、RadiusNeighborsRegressor
1)基本用法
sklearn.neighbors.RadiusNeighborsRegressor(radius=1.0, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
2)參數(shù)詳解
參考RadiusNeighborsClassifier,參數(shù)少了outlier_label,因?yàn)闊o需分類,其他一模一樣的參數(shù)、和方法
3)案例詳解
X = [[0], [1], [2], [3]]
y = [0, 0.5, 1.8, 2]
from sklearn.neighbors import RadiusNeighborsRegressor
neigh = RadiusNeighborsRegressor(radius=1.0)
neigh.fit(X, y)
print(neigh.predict([[1.3]]))
[1.15]
5、NearestCentroid
常規(guī)的KNN分類,如果有1億個(gè)訓(xùn)練樣本,那么就要求計(jì)算1億個(gè)距離,然后對(duì)這1億個(gè)跨度進(jìn)行排序,取最近的K個(gè)鄰居,顯然數(shù)量大了,算法運(yùn)行效率就低了,基于此,質(zhì)心分類提出了一種全新的思路,利用樣本質(zhì)心來判定類別,如果已知樣本有1億個(gè),共有3個(gè)類別,先計(jì)算出3個(gè)質(zhì)心,那么在進(jìn)行分類時(shí),只要把預(yù)測(cè)數(shù)據(jù)與3個(gè)類別的質(zhì)心求3次距離并求一個(gè)最小值,這極大地提高了運(yùn)行效率。示意圖如下:
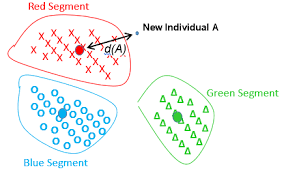
該 NearestCentroid 分類器是一個(gè)簡(jiǎn)單的算法, 它表示每個(gè)類都通過其成員的質(zhì)心組成, 實(shí)際上, 這使得它類似于 KMeans算法的標(biāo)簽更新階段,它也沒有參數(shù)選擇,使其成為良好的基準(zhǔn)分類器。
1)基本用法
sklearn.neighbors.NearestCentroid(metric='euclidean', *,
shrink_threshold=None)
星號(hào)(*):這是PEP-3102和Python3.0引入的一種新的函數(shù)參數(shù)規(guī)范語法,它指示KNeighborsClassifier類的構(gòu)造函數(shù)在n_neighbors之后不接受任何其他位置參數(shù),其余所有參數(shù)都是僅關(guān)鍵字的。僅關(guān)鍵字參數(shù)與名稱和值一起提供,而位置參數(shù)則不必提供。在這種情況下,您可以合法地使用以下語法(為n_neighbors提供值)
2)參數(shù)說明
shrink_threshold:最近縮小質(zhì)心, 它實(shí)現(xiàn)了 nearest shrunken centroid 分類器.,實(shí)際上, 每個(gè)質(zhì)心的每個(gè)特征的值除以該特征的類中的方差, 然后通過shrink_threshold 來減小特征值, 最值得注意的是,如果特定特征值與零相交, 則將其設(shè)置為零. 實(shí)際上, 這將從影響的分類上刪除該特征. 這是有用的, 例如, 去除噪聲特征。
3)Attributes
centroids_:每個(gè)類別的質(zhì)心
classes_:訓(xùn)練集類別的數(shù)量
n_features_in_:特征的數(shù)量
feature_names_in_:查看特征的名稱
4)案例分析
from sklearn.neighbors import NearestCentroid
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
y = np.array([1, 1, 1, 2, 2, 2])
clf = NearestCentroid()
clf.fit(X, y)
NearestCentroid()
print(clf.predict([[-0.8, -1]]))
[1]
# 查看質(zhì)心
clf.centroids_
array([[-2. , -1.33333333],
[ 2. , 1.33333333]])
6、K值的確定
我們用數(shù)據(jù)集load_digits進(jìn)行數(shù)據(jù)評(píng)估,使用常規(guī)的算法KNeighborsClassifier
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
digits = datasets.load_digits()
X_digits = digits.data
y_digits = digits.target
# 查看下數(shù)據(jù)集的大小
X_digits.shape
(1797, 64)
# 數(shù)據(jù)集進(jìn)行拆分,按3-7比例分為測(cè)試集+訓(xùn)練集
X_train, X_test, y_train, y_test = train_test_split(\
X_digits,
y_digits,
test_size=0.3,
random_state=250
)
# 尋找最優(yōu)k值
best_s = 0
best_k = -1
k_list = [] #存儲(chǔ)K值
s_list = [] #存儲(chǔ)準(zhǔn)確率值
for k in range(1,10):
clf = KNeighborsClassifier(k,weights='distance')
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
k_list.append(k)
s_list.append(score)
if score > best_s:
best_s = score
best_k = k
plt.plot(k_list, score_list, color='steelblue')
plt.show()
print('最好的參數(shù)k為{}'.format(best_k))
print('最好準(zhǔn)確率為{}'.format(best_s))
最好的參數(shù)k為1
最好準(zhǔn)確率為0.9907407407407407
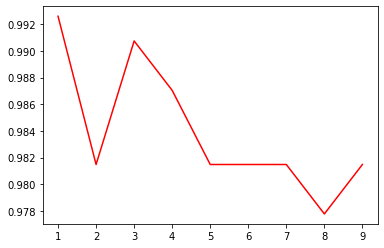
可以看出,k=1的時(shí)候,準(zhǔn)確率最高,并且隨著K的增加,準(zhǔn)確率在不斷的下降,這個(gè)數(shù)據(jù)比較特殊,一般都是K值取一個(gè)10左右比較高。對(duì)于自己的數(shù)據(jù)集,可以根據(jù)實(shí)際情況進(jìn)行調(diào)整。
7、KNN優(yōu)缺點(diǎn)
KNN算法真是個(gè)愛憎分明的算法,優(yōu)點(diǎn)缺點(diǎn)都特別明顯,哈哈,我找了一堆,大家可以慢慢體會(huì),發(fā)現(xiàn)還是缺點(diǎn)多很多。具體總結(jié)如下,很多缺點(diǎn)也慢慢的進(jìn)行了優(yōu)化和解決。
1)優(yōu)? 點(diǎn)
原理簡(jiǎn)單,易于理解和實(shí)現(xiàn)
無需參數(shù),也不用實(shí)際進(jìn)行訓(xùn)練
比較適用于多分類問題
kNN可以用來做無監(jiān)督異常檢驗(yàn);
自適應(yīng)kNN可以根據(jù)不同的區(qū)域,在局部選擇不同的k
kNN非常適合做時(shí)間序列
2)缺? 點(diǎn)
基于KNN模型尋找異常點(diǎn)是不適合于高維數(shù)據(jù)和大批量數(shù)據(jù)的,kNN算法必須保存全部的數(shù)據(jù)集,如果訓(xùn)練數(shù)據(jù)集很大,那么就需要耗費(fèi)大量的存儲(chǔ)空間。此外,由于必須對(duì)待分類數(shù)據(jù)計(jì)算與每一個(gè)訓(xùn)練數(shù)據(jù)的距離,非常耗時(shí)。
而且距離的計(jì)算采用的是歐式距離公式,只能針對(duì)球形簇的樣本數(shù)據(jù)尋找異常,對(duì)于非球形簇則無法很好的搜尋異常。
可解釋性較差,無法給出決策樹那樣的規(guī)則,對(duì)變量的縮放非常敏感、無法處理categorical變量、難以處理不同單位和不同數(shù)值范圍的變量
kNN還有個(gè)問題就是k的選擇。k總是在過擬合與欠擬合之間游走。你可以說通過cross validation來選k,可是呢,你選出的k是全局適用的,而每個(gè)局部都是這個(gè)k最佳。所以kNN總是無法避免地在一些區(qū)域過擬合,同時(shí)在另一些區(qū)域欠擬合。
如果用K近鄰模型做回歸的話,一個(gè)比較明顯的缺陷,就是K-NN無法做out of sample的回歸預(yù)測(cè)。因?yàn)橛肒-NN做回歸的時(shí)候,預(yù)測(cè)值是它附近幾個(gè)值的平均值。所以預(yù)測(cè)值不可能超過預(yù)測(cè)樣本的最大值,也不可能小于樣本的最小值。這個(gè)缺點(diǎn)其實(shí)是和回歸樹一樣的。
k太小,容易受到噪聲數(shù)據(jù)影響,k太大可能在近鄰中包含其它類別的點(diǎn),可通過對(duì)距離加權(quán)解決,已經(jīng)有這個(gè)參數(shù)了。
三、圖解KNN異常檢算法KNN怎么進(jìn)行無監(jiān)督檢測(cè)呢,其實(shí)也是很簡(jiǎn)單的,異常點(diǎn)是指遠(yuǎn)離大部分正常點(diǎn)的樣本點(diǎn),再直白點(diǎn)說,異常點(diǎn)一定是跟大部分的樣本點(diǎn)都隔得很遠(yuǎn)。基于這個(gè)思想,我們只需要依次計(jì)算每個(gè)樣本點(diǎn)與它最近的K個(gè)樣本的平均距離,再利用計(jì)算的距離與閾值進(jìn)行比較,如果大于閾值,則認(rèn)為是異常點(diǎn),同樣,為了幫助讀者理解如何利用KNN思想,實(shí)現(xiàn)異常值的識(shí)別,我畫了下面這張圖。對(duì)于第一個(gè),3個(gè)鄰居的平均距離為(2+2+3)/3=2.33,對(duì)于第二點(diǎn),3個(gè)鄰居的平均距離為(7+8+5)/3=6.667,明顯,第二個(gè)點(diǎn)的異常程度要高與第一個(gè)點(diǎn)。
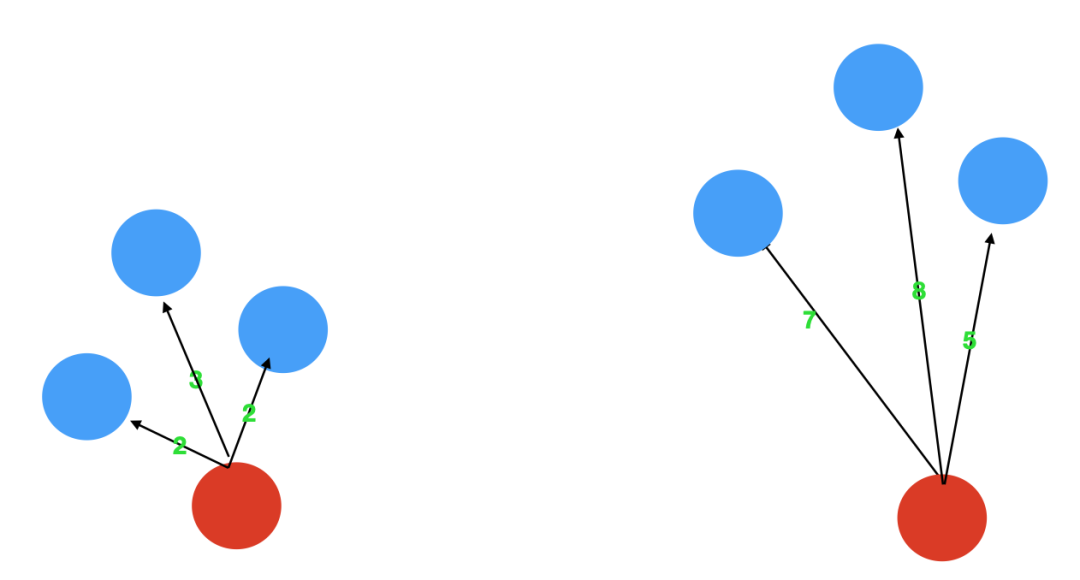
優(yōu)點(diǎn)是不需要假設(shè)數(shù)據(jù)的分布,缺點(diǎn)是不適合高維數(shù)據(jù)、只能找出異常點(diǎn),無法找出異常簇、你每一次計(jì)算近鄰距離都需要遍歷整個(gè)數(shù)據(jù)集,不適合大數(shù)據(jù)及在線應(yīng)用、有人用hyper-grid技術(shù)提速將KNN應(yīng)用到在線情況,但是還不是足夠快,僅可以找出全局異常點(diǎn),無法找到局部異常點(diǎn)。
KNN異常檢測(cè)過程:對(duì)未知類別的數(shù)據(jù)集中的每個(gè)點(diǎn)依次執(zhí)行以下操作:
1) 計(jì)算當(dāng)前點(diǎn) 與 數(shù)據(jù)集中每個(gè)點(diǎn)的距離
2) 按照距離遞增次序排序
3) 選取與當(dāng)前點(diǎn)距離最小的k個(gè)點(diǎn)
4) 計(jì)算當(dāng)前點(diǎn)與K個(gè)鄰居的距離,并取均值、或者中值、最大值三個(gè)中的一個(gè)作為異常值
1、異常實(shí)例計(jì)算
無監(jiān)督,我們就要標(biāo)簽去掉,為了演示過程,我們引進(jìn)了9號(hào)嘉賓,這個(gè)人非常自信,每一項(xiàng)都填的非常高,明顯異常,我們的目的就是要把這種類似的錯(cuò)誤找出來。
2、距離計(jì)算和排序
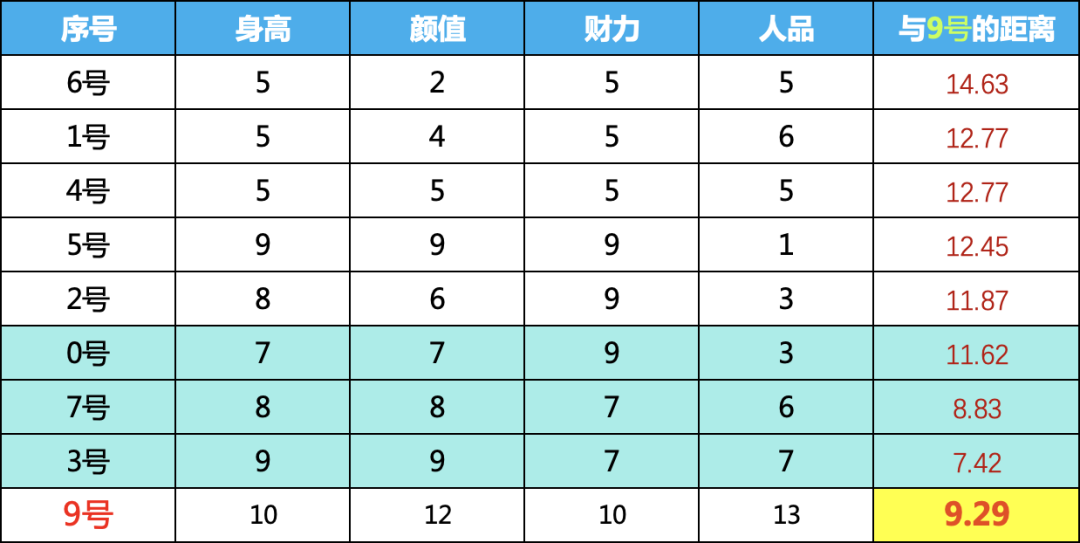
我們計(jì)算9號(hào)的異常程度,我們這里把計(jì)算和排序兩步統(tǒng)一到一起了
先計(jì)算9號(hào)與其他樣本的距離,然后排序,取最近的三個(gè),我們計(jì)算平均距離,可以看到,9號(hào)與最近的三個(gè)鄰居的平均距離是9.29
3、計(jì)算距離值
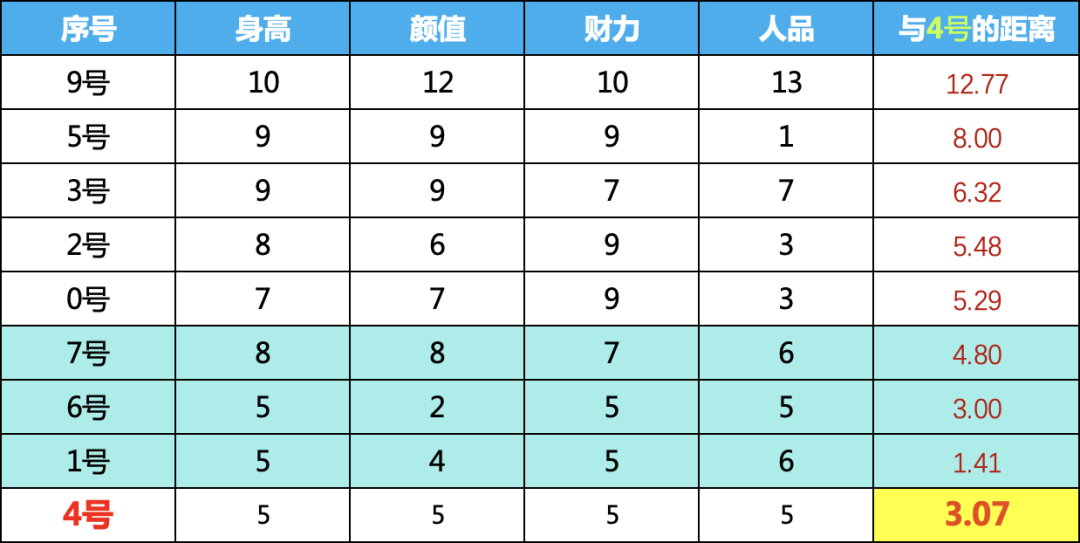
我們?cè)儆?jì)算4號(hào)嘉賓的距離,可以看到,最近的三個(gè)鄰居與4號(hào)的平均距離為3.07,只是9號(hào)的三分之一,相對(duì)來說就比較正常了。當(dāng)然距離計(jì)算可以用最大值,平均值,中位數(shù)三個(gè),算法中通過method這個(gè)參數(shù)進(jìn)行調(diào)節(jié)。
我們依次計(jì)算,就可以得到每個(gè)樣本3個(gè)鄰居的平均距離了,越高的越異常,我們也可以用Python的包來檢測(cè)下我們計(jì)算的對(duì)不對(duì)。
import numpy as np
X_train = np.array([
[7, 7, 9, 3],
[5, 4, 5, 6],
[8, 6, 9, 3],
[9, 9, 7, 7],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 8, 7, 6],
[10,10, 12, 13]])
# import kNN分類器
from pyod.models.knn import KNN
# 訓(xùn)練一個(gè)kNN檢測(cè)器
clf_name = 'kNN'
# 初始化檢測(cè)器clf
clf = KNN( method='mean', n_neighbors=3, )
clf.fit(X_train)
# 返回訓(xùn)練數(shù)據(jù)X_train上的異常標(biāo)簽和異常分值
# 返回訓(xùn)練數(shù)據(jù)上的分類標(biāo)簽 (0: 正常值, 1: 異常值)
y_train_pred = clf.labels_
y_train_pred
array([0, 0, 0, 0, 0, 0, 0, 0, 1])
# 返回訓(xùn)練數(shù)據(jù)上的異常值 (分值越大越異常)
y_train_scores = clf.decision_scores_
y_train_scores
array([2.91709951, 3.01181545, 3.09299219, 4.16692633, 3.07001503,
4.25784112, 3.98142397, 3.24271326, 9.42068891])
我們自己計(jì)算的平均距離為9.29,系統(tǒng)算的9.42,有一點(diǎn)點(diǎn)的差異,可能是哪里加了一個(gè)微調(diào)的系數(shù),大家可以探索下。
四、KNN異常檢測(cè)算法應(yīng)用上面大概知道了KNN怎么進(jìn)行異常檢測(cè)的,現(xiàn)在我們找個(gè)具體的案例,看看更加明細(xì)的參數(shù)以及實(shí)現(xiàn)的過程,有個(gè)更加立體的感覺,并且學(xué)完能夠應(yīng)用起來。
1、算法基本用法
地址:https://pyod.readthedocs.io/en/latest/pyod.models.html#module-pyod.models.knn
pyod.models.knn.KNN(contamination=0.1,
n_neighbors=5,
method='largest',
radius = 1.0,
algorithm='auto',
leaf_size=30,
metric='minkowski',
p=2,
metric_params=None,
n_jobs=1,
**kwargs)
2、參數(shù)詳解
contamination:污染度,contamination : float in (0., 0.5), optional (default=0.1)數(shù)據(jù)集的污染量,即數(shù)據(jù)集中異常值的比例。在擬合時(shí)用于定義決策函數(shù)的閾值。如果是“自動(dòng)”,則確定決策函數(shù)閾值,如原始論文中所示。在版本0.20中更改:默認(rèn)值contamination將從0.20更改為'auto'0.22。
n_neighbors:選取相鄰點(diǎn)數(shù)量
method:‘largest’、‘mean’、‘median’
largest:使用與第k個(gè)相鄰點(diǎn)的距離作為異常得分
mean:使用k個(gè)相鄰點(diǎn)距離的平均值作為異常得分
median:使用k個(gè)相鄰點(diǎn)距離的中值作為異常得分
radius : radius_neighbors使用的參數(shù)空間半徑
algorithm:找到最近的k個(gè)樣本
kd_tree:依次對(duì)K維坐標(biāo)軸,以中值切分,每一個(gè)節(jié)點(diǎn)是超矩形,適用于低維(<20時(shí)效率最高)
ball_tree:以質(zhì)心c和半徑r分割樣本空間,每一個(gè)節(jié)點(diǎn)是超球體,適用于高維(kd_tree高維效率低)
brute:暴力搜索
auto:通過 fit() 函數(shù)擬合,選擇最適合的算法;如果數(shù)據(jù)稀疏,擬合后會(huì)自動(dòng)選擇brute,參數(shù)失效
leaf_size:kd_tree和ball_tree中葉子大小,影響構(gòu)建、查詢、存儲(chǔ),根據(jù)實(shí)際數(shù)據(jù)而定。樹葉中可以有多于一個(gè)的數(shù)據(jù)點(diǎn),算法在達(dá)到葉子時(shí)在其中執(zhí)行暴力搜索即可。如果leaf size 趨向于 N(訓(xùn)練數(shù)據(jù)的樣本數(shù)量),算法其實(shí)就是 brute force了。如果leaf size 太小了,趨向于1,那查詢的時(shí)候 遍歷樹的時(shí)間就會(huì)大大增加。
metric:距離計(jì)算標(biāo)準(zhǔn),距離標(biāo)準(zhǔn)圖例
euclidean:歐氏距離(p = 2)
manhattan:曼哈頓距離(p = 1)
minkowski:閔可夫斯基距離
p : metric參數(shù),默認(rèn)為2
metric_params : metric參數(shù)
n_jobs : 并行作業(yè)數(shù),-1時(shí),n_jobs為CPU核心數(shù)。
3、屬性詳解
decision_scores_:數(shù)據(jù)X上的異常打分,分?jǐn)?shù)越高,則該數(shù)據(jù)點(diǎn)的異常程度越高
threshold_:異常樣本的個(gè)數(shù)閾值,基于contamination這個(gè)參數(shù)的設(shè)置,總量最多等于n_samples * contamination
labels_: 數(shù)據(jù)X上的異常標(biāo)簽,返回值為二分類標(biāo)簽(0為正常點(diǎn),1為異常點(diǎn))
4、方法詳解
fit(X): 用數(shù)據(jù)X來“訓(xùn)練/擬合”檢測(cè)器clf。即在初始化檢測(cè)器clf后,用X來“訓(xùn)練”它。
fit_predict_score(X, y): 用數(shù)據(jù)X來訓(xùn)練檢測(cè)器clf,并預(yù)測(cè)X的預(yù)測(cè)值,并在真實(shí)標(biāo)簽y上進(jìn)行評(píng)估。此處的y只是用于評(píng)估,而非訓(xùn)練
decision_function(X): 在檢測(cè)器clf被fit后,可以通過該函數(shù)來預(yù)測(cè)未知數(shù)據(jù)的異常程度,返回值為原始分?jǐn)?shù),并非0和1。返回分?jǐn)?shù)越高,則該數(shù)據(jù)點(diǎn)的異常程度越高
predict(X): 在檢測(cè)器clf被fit后,可以通過該函數(shù)來預(yù)測(cè)未知數(shù)據(jù)的異常標(biāo)簽,返回值為二分類標(biāo)簽(0為正常點(diǎn),1為異常點(diǎn))
predict_proba(X): 在檢測(cè)器clf被fit后,預(yù)測(cè)未知數(shù)據(jù)的異常概率,返回該點(diǎn)是異常點(diǎn)概率
當(dāng)檢測(cè)器clf被初始化且fit(X)函數(shù)被執(zhí)行后,clf就會(huì)生成兩個(gè)重要的屬性:
decision_scores: 數(shù)據(jù)X上的異常打分,分?jǐn)?shù)越高,則該數(shù)據(jù)點(diǎn)的異常程度越高
KNN算法專注于全局異常檢測(cè),所以無法檢測(cè)到局部異常。首先,對(duì)于數(shù)據(jù)集中的每條記錄,必須找到k個(gè)最近的鄰居。然后使用這K個(gè)鄰居計(jì)算異常分?jǐn)?shù)。
最 ? 大:使用到第k個(gè)鄰居的距離作為離群值得分
平均值:使用所有k個(gè)鄰居的平均值作為離群值得分
中位數(shù):使用到k個(gè)鄰居的距離的中值作為離群值得分
在實(shí)際方法中后兩種的應(yīng)用度較高。然而,分?jǐn)?shù)的絕對(duì)值在很大程度上取決于數(shù)據(jù)集本身、維度數(shù)和規(guī)范化。參數(shù)k的選擇當(dāng)然對(duì)結(jié)果很重要。如果選擇過低,記錄的密度估計(jì)可能不可靠。(即過擬合)另一方面,如果它太大,密度估計(jì)可能太粗略。K值的選擇通常在10-50這個(gè)范圍內(nèi)。所以在分類方法中,選擇一個(gè)合適的K值,可以用交叉驗(yàn)證法。
但是,事實(shí)上基于KNN的算法都是不適用于欺詐檢測(cè)的,因?yàn)樗麄儽旧砭蛯?duì)噪聲比較敏感。
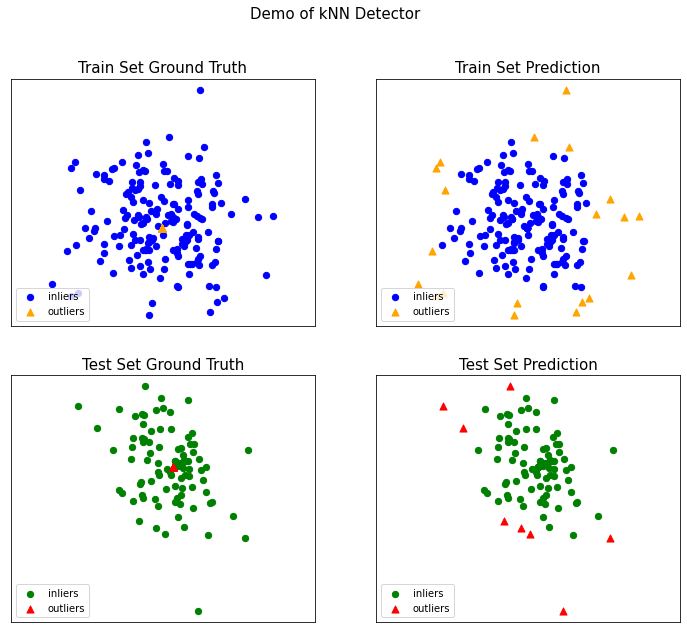
5、案例分析
#導(dǎo)入
from pyod.models.knn import KNN
from pyod.utils.data import generate_data
from pyod.utils.data import evaluate_print
from pyod.utils.example import visualize
#參數(shù)設(shè)置
contamination = 0.1 # percentage of outliers
n_train = 200 # number of training points
n_test = 100 # number of testing points
X_train, y_train, X_test, y_test = generate_data(
n_train=n_train, n_test=n_test, contamination=contamination)
# import kNN分類器
from pyod.models.knn import KNN
# 訓(xùn)練一個(gè)kNN檢測(cè)器
clf_name = 'kNN'
clf = KNN() # 初始化檢測(cè)器clf
clf.fit(X_train) # 使用X_train訓(xùn)練檢測(cè)器clf
# 返回訓(xùn)練數(shù)據(jù)X_train上的異常標(biāo)簽和異常分值
y_train_pred = clf.labels_ # 返回訓(xùn)練數(shù)據(jù)上的分類標(biāo)簽 (0: 正常值, 1: 異常值)
y_train_scores = clf.decision_scores_ # 返回訓(xùn)練數(shù)據(jù)上的異常值 (分值越大越異常)
# 用訓(xùn)練好的clf來預(yù)測(cè)未知數(shù)據(jù)中的異常值
y_test_pred = clf.predict(X_test) # 返回未知數(shù)據(jù)上的分類標(biāo)簽 (0: 正常值, 1: 異常值)
y_test_scores = clf.decision_function(X_test) # 返回未知數(shù)據(jù)上的異常值 (分值越大越異常)
對(duì)識(shí)別結(jié)果可視化
# 模型可視化
visualize(clf_name,
X_train,
y_train,
X_test,
y_test,
y_train_pred,
y_test_pred,
show_figure=True,
save_figure=False
)
KNN除了能夠進(jìn)行有監(jiān)督,另外幾個(gè)在sklearn.neighbors包中但不是做分類、回歸預(yù)測(cè)的類也值得關(guān)注,用于尋找最鄰近的數(shù)據(jù)點(diǎn),是其他最鄰近算法的基礎(chǔ)。kneighbors_graph類返回用KNN時(shí)和每個(gè)樣本最近的K個(gè)訓(xùn)練集樣本的位置。radius_neighbors_graph返回用限定半徑最近鄰法時(shí)和每個(gè)樣本在限定半徑內(nèi)的訓(xùn)練集樣本的位置。NearestNeighbors是個(gè)大雜燴,它即可以返回用KNN時(shí)和每個(gè)樣本最近的K個(gè)訓(xùn)練集樣本的位置,也可以返回用限定半徑最近鄰法時(shí)和每個(gè)樣本最近的訓(xùn)練集樣本的位置,常常用在聚類模型中。
許多學(xué)習(xí)方法都是依賴最近鄰作為核心。一個(gè)例子是 核密度估計(jì) 和LOF, 這兩個(gè)我們?cè)谄渌胤皆儆懻?/span>
1、NearestNeighbors
NearestNeighbors (最近鄰)尋找N個(gè)最近的鄰居以及計(jì)算之間的距離,實(shí)現(xiàn)了 unsupervised nearest neighbors learning(無監(jiān)督的最近鄰學(xué)習(xí))。它為三種不同的最近鄰算法提供統(tǒng)一的接口:BallTree, KDTree, 還有基于 sklearn.metrics.pairwise 的 brute-force 算法。選擇算法時(shí)可通過關(guān)鍵字 'algorithm' 來控制, 并指定為 ['auto', 'ball_tree', 'kd_tree', 'brute'] 其中的一個(gè)即可。當(dāng)默認(rèn)值設(shè)置為 'auto' 時(shí),算法會(huì)嘗試從訓(xùn)練數(shù)據(jù)中確定最佳方法。
1)基本用法
sklearn.neighbors.NearestNeighbors(*, n_neighbors=5, radius=1.0, algorithm='auto', leaf_size=30, metric='minkowski', p=2, metric_params=None, n_jobs=None)
2)參數(shù)含義
n_neighbors(n鄰域):所要選用的最近鄰的數(shù)目,相當(dāng)于knn算法(k近鄰算法)中的 k,(default = 5),在設(shè)置此參數(shù)時(shí)輸入的需為整形(int)。
radius(半徑):要使用的參數(shù)空間范圍,在設(shè)置此參數(shù)時(shí)輸入的需為浮點(diǎn)數(shù)(float)。
algorithm{‘a(chǎn)uto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}:即用于選取計(jì)算最近鄰的算法:這里主要包括
‘a(chǎn)uto’ ? ? ?:根據(jù)樣本數(shù)據(jù)自動(dòng)刷選合適的算法。
‘ball_tree’:構(gòu)建“球樹”算法模型。
‘kd_tree’ :‘’kd樹‘’算法。
‘brute’ ? ? :使用蠻力搜索,即或相當(dāng)于Knn算法,需遍歷所有樣本數(shù)據(jù)與目標(biāo)數(shù)據(jù)的距離,進(jìn)而按升序排序從而選取最近的K個(gè)值,采用投票得出結(jié)果。
leaf_size:葉的大小,針對(duì)算法為球樹或KD樹而言。這個(gè)設(shè)置會(huì)影響構(gòu)造和查詢的速度,以及存儲(chǔ)樹所需的內(nèi)存。最優(yōu)值取決于問題的性質(zhì)。
metric:用于樹的距離度量。默認(rèn)度量是Minkowski,p=2等價(jià)于標(biāo)準(zhǔn)的歐幾里德度量。有關(guān)可用度量的列表,可以查閱距離度量類的文檔。如果度量是“預(yù)先計(jì)算的”,則假定X是距離矩陣,在擬合期間必須是平方。
p:Minkowski度量參數(shù)的參數(shù)來自sklearn.emeics.pairwise.pairwise_距離。當(dāng)p=1時(shí),這等價(jià)于使用曼哈頓距離(L1),歐幾里得距離(L2)等價(jià)于p=2時(shí),對(duì)于任意的p,則使用Minkowski_距離(L_P)。
metric_params:度量函數(shù)的附加關(guān)鍵字參數(shù),設(shè)置應(yīng)為dict(字典)形式。
n_jobs:要為鄰居搜索的并行作業(yè)的數(shù)量。None指1,除非在 joblib.parallel_backend背景。-1意味著使用所有處理器,若要了解相關(guān)的知識(shí)應(yīng)該具體查找一下。
3)案例解析
from sklearn.neighbors import NearestNeighbors
import numpy as np
#定義一個(gè)數(shù)組
X = np.array([[-1,-1],
[-2,-1],
[-3,-2],
[1,1],
[2,1],
[3,2] ])
nbrs = NearestNeighbors(n_neighbors=3, algorithm= 'ball_tree').fit(X)
distances, indices = nbrs.kneighbors(X)
# 訓(xùn)練一個(gè)模型,并計(jì)算距離
samples = [[0, 0, 2], [1, 0, 0], [0, 0, 1]]
neigh = NearestNeighbors(n_neighbors=2,
radius=0.4,
algorithm='ball_tree')
neigh.fit(samples)
neigh.kneighbors([[0, 0, 1.3]], 2,
return_distance=True, )
distances, neighs = neigh.kneighbors([[0, 0, 1.3]], 2, return_distance=True, )
distances
array([[0.3, 0.7]])
neighs
array([[2, 0]], dtype=int64)
from sklearn.neighbors import NearestNeighbors
import numpy as np
X = np.array([
[7, 7, 9, 3],
[5, 4, 5, 6],
[3, 6, 6, 9],
[9, 9, 7, 5],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 8, 7, 6]])
nbrs = NearestNeighbors(n_neighbors=3, algorithm= 'ball_tree').fit(X)
distances, indices = nbrs.kneighbors([[9, 9, 9, 2]])
2、KDTree 和 BallTree 類
我們可以使用 KDTree 或 BallTree 其中一個(gè)類來找最近鄰。這是上文使用過的 NearestNeighbors 類所包含的功能。KDTree 和 BallTree 具有相同的接口;我們將在這里展示使用 KDTree 的例子
1)BallTree
sklearn.neighbors.BallTree(X, leaf_size=40, metric='minkowski', **kwargs)
21)KDTree
sklearn.neighbors.KDTree(X, leaf_size=40, metric='minkowski', **kwargs)?
3)案例應(yīng)用
from sklearn.neighbors import KDTree
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
kdt = KDTree(X, leaf_size=30, metric='euclidean')
kdt.query(X, k=2, return_distance=False)
array([[0, 1],
[1, 0],
[2, 1],
[3, 4],
[4, 3],
[5, 4]]...)
計(jì)算距離,方便其他算法進(jìn)行調(diào)用。
3、kneighbors_graph
k-近鄰圖(k-nearest neighbor graph),選定參數(shù)k,對(duì)于頂點(diǎn)vi,i=1,..,n,把離它最近的k個(gè)點(diǎn)與之相連,所得到的圖就是k-近鄰圖。需要注意的是,因?yàn)檫@樣的鄰近關(guān)系并不是對(duì)稱的(vj是vi的k近鄰 ≠vi是vj的k近鄰),故而得到的圖將會(huì)是“有向”的。為了得到無向的圖(圖的賦權(quán)鄰接矩陣W應(yīng)是對(duì)稱的)
1)基本用法
sklearn.neighbors.kneighbors_graph(X, n_neighbors, *, mode='connectivity', metric='minkowski', p=2, metric_params=None, include_self=False, n_jobs=None)
2)參數(shù)詳解
X:樣本數(shù)據(jù),以numpy數(shù)組或預(yù)先計(jì)算的BallTree的形式。
n_neighbors:每個(gè)樣本的鄰居數(shù)量。
mode:'connectivity'將返回具有1和0的連通性矩陣,而'distance'將根據(jù)給定的度量返回鄰居之間的距離。
metric:用于計(jì)算每個(gè)采樣點(diǎn)的k鄰居的距離度量。DistanceMetric類提供了可用指標(biāo)的列表。默認(rèn)距離為'euclidean'(“ minkowski”度量標(biāo)準(zhǔn),p參數(shù)等于2。)
p:Minkowski度量的功率參數(shù)。當(dāng)p=1時(shí),相當(dāng)于使用manhattan_distance (l1),p=2時(shí)使用歐氏距離(l2)。對(duì)于任意的p,使用minkowski_distance (l_p)。
metric_params:計(jì)量函數(shù)的附加關(guān)鍵字參數(shù)。
include_self:是否將每個(gè)樣本標(biāo)記為其自身的第一個(gè)最近鄰居。如果為'auto',則將True用于mode ='connectivity',將False用于mode ='distance'。
n_job:為鄰居搜索運(yùn)行的并行作業(yè)數(shù)。None 意味著 1 除非在joblib.parallel_backend上下文中。-1 表示使用所有處理器。
返回值:圖形,其中A[i,j]被賦予連接i和j的邊的權(quán)重,矩陣為CSR格式。
3)案例數(shù)據(jù)
可以看到,這里的聯(lián)通,包含了自己,當(dāng)鄰居等于1的時(shí)候,只有自己和自己聯(lián)通
X = [[0], [3], [1]]
from sklearn.neighbors import kneighbors_graph
A = kneighbors_graph(X, 2, mode='connectivity', include_self=True)
A.toarray()
array([[1., 0., 1.],
[0., 1., 1.],
[1., 0., 1.]])
X = [[0], [3], [1]]
from sklearn.neighbors import kneighbors_graph
A = kneighbors_graph(X,1, mode='connectivity', include_self=True)
A.toarray()
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
4)數(shù)據(jù)可視化
https://blog.csdn.net/pylittlebrat/article/details/121914230
import networkx as nx
import matplotlib.pyplot as plt
X = np.array([[7, 7, 9, 3],
[5, 4, 5, 6],
[8, 6, 9, 3],
[9, 9, 7, 7],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 2, 7, 6],
[1, 8, 7, 4],
[4, 3, 7, 8],
[8, 1, 7, 6]
])
from sklearn.neighbors import kneighbors_graph
A = kneighbors_graph(X, 4, mode='connectivity', include_self=False)
# 繪圖
G = nx.from_numpy_matrix(A.toarray())
plt.figure(figsize=(4,4),dpi=600)
nx.draw_networkx(G,
pos = nx.kamada_kawai_layout(G),
node_color = 'r',
node_size=500,
alpha=0.8
)
plt.axis('off')
plt.show()
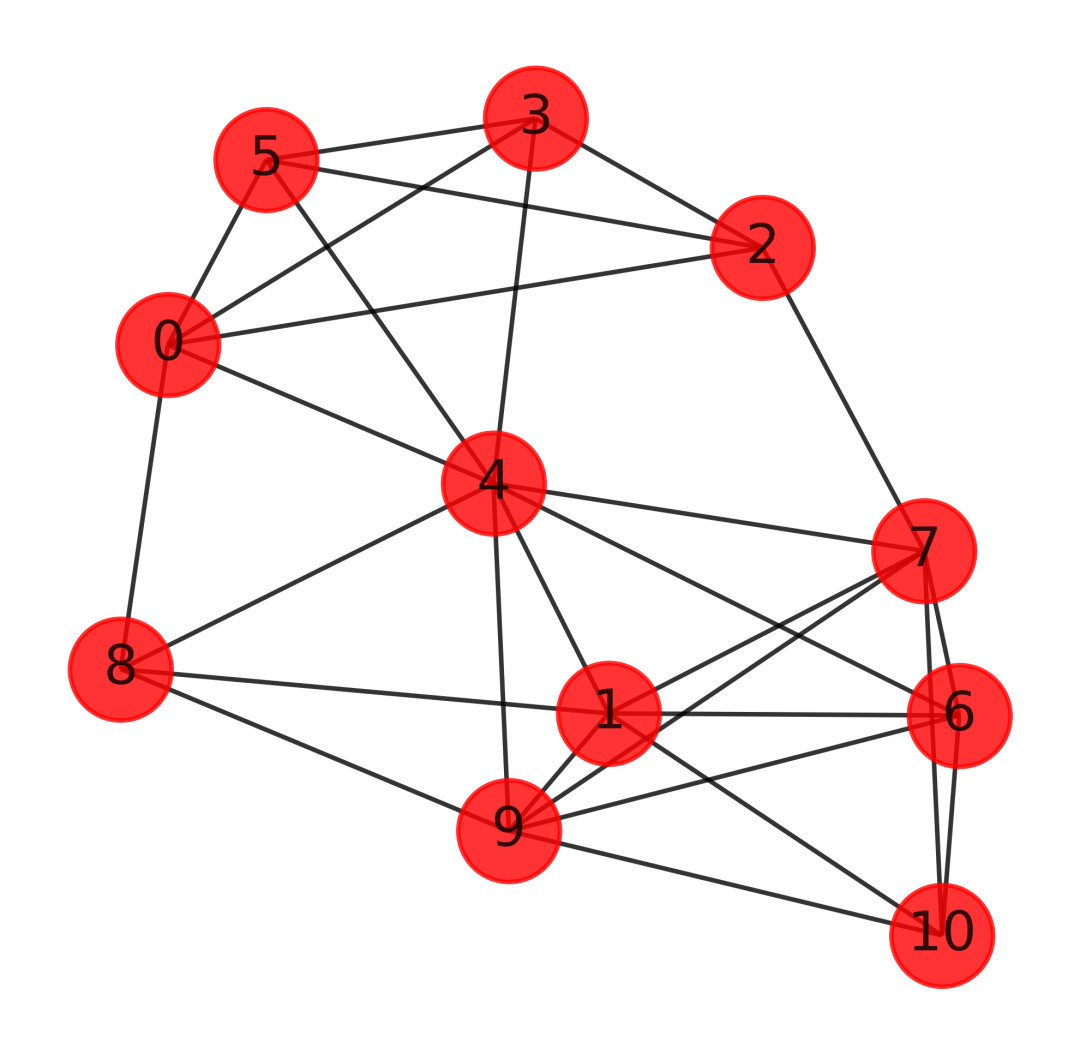
我們這里的圖比較簡(jiǎn)單,如果繼續(xù)增加復(fù)雜度,畫出的圖如下,大家可以找比較大的數(shù)據(jù)集進(jìn)行測(cè)試,文章寫的太多了,不能再寫下去了。KNN寫成圖算法了。

https://www.cylab.be/blog/47/distributed-k-nn-graphs-and-similarity-search
4、radius_neighbors_graph
1)基本用法
sklearn.neighbors.radius_neighbors_graph(X, radius, *, mode='connectivity', metric='minkowski', p=2, metric_params=None, include_self=False, n_jobs=None)
2)參數(shù)詳解
參考kneighbors_graph,除了半徑限制參數(shù)radius,其他的參數(shù)均一模一樣,這里不再贅述。
3)應(yīng)用案例
X = [[0], [3], [1]]
from sklearn.neighbors import radius_neighbors_graph
A = radius_neighbors_graph(X, 1.5, mode='connectivity',
include_self=True)
A.toarray()
array([[1., 0., 1.],
[0., 1., 0.],
[1., 0., 1.]])
4)可視化
import networkx as nx
import matplotlib.pyplot as plt
X = np.array([[7, 7, 9, 3],
[5, 4, 5, 6],
[8, 6, 9, 3],
[9, 9, 7, 7],
[5, 5, 5, 5],
[9, 9, 9, 1],
[5, 2, 5, 5],
[8, 2, 7, 6],
[1, 8, 7, 4],
[4, 3, 7, 8],
[8, 1, 7, 6]
])
from sklearn.neighbors import kneighbors_graph
A = radius_neighbors_graph(X, 4, mode='connectivity', include_self=False)
# 繪圖
G = nx.from_numpy_matrix(A.toarray())
plt.figure(figsize=(4,4),dpi=600)
nx.draw_networkx(G,
pos = nx.kamada_kawai_layout(G),
node_color = 'r',
node_size=500,
alpha=0.8
)
plt.axis('off')
plt.show()
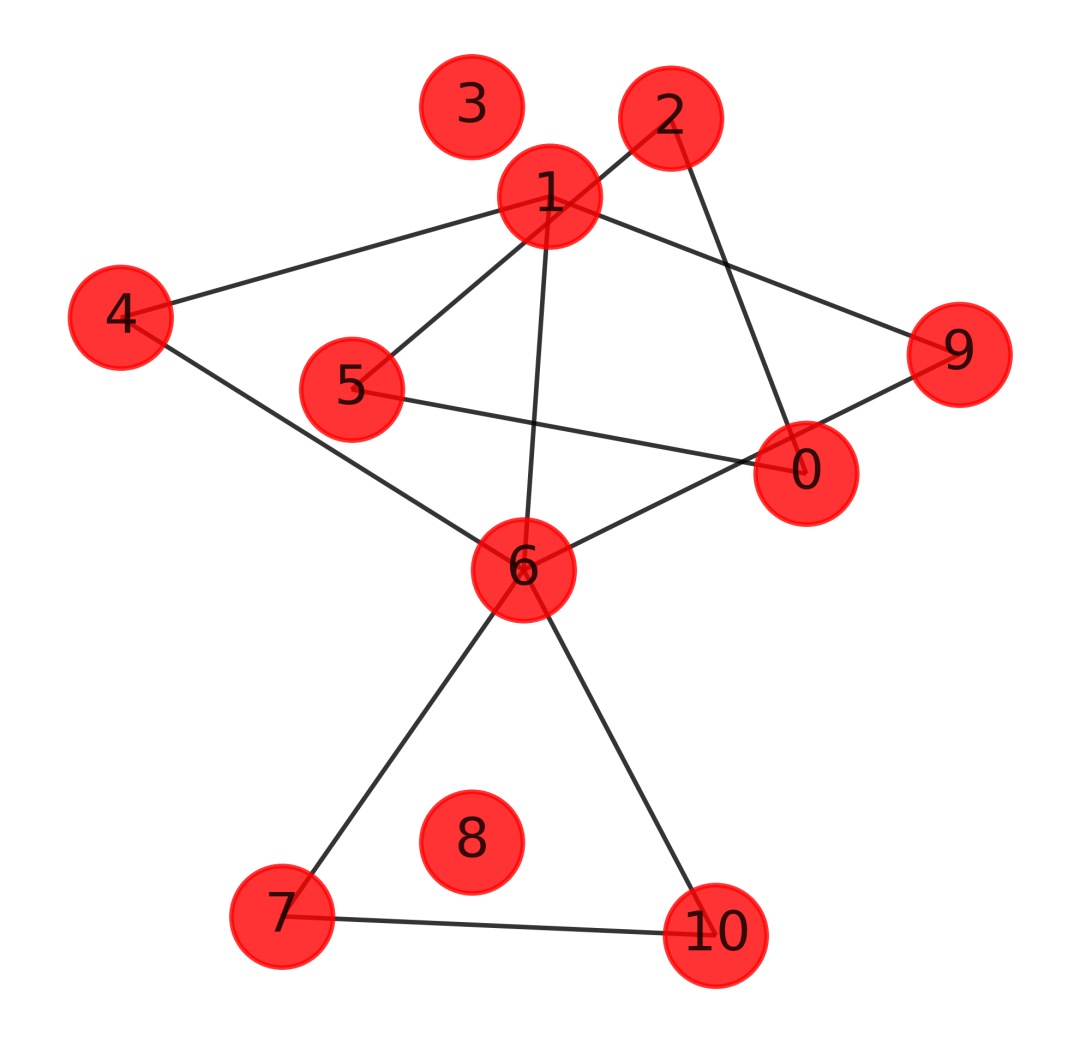
可以看到,我們的半徑設(shè)置為4,有的節(jié)點(diǎn)并沒有找到鄰居,我們自己的用戶或者文本數(shù)據(jù),也是可以通過構(gòu)建類似的矩陣,然后計(jì)算每個(gè)樣本的K相似或者半徑相識(shí),這樣就能夠一目了然的找出一堆樣本相互之間的關(guān)系了,并且還可以考慮其中的權(quán)重。
六、總 ?結(jié)通過本文,我們發(fā)現(xiàn)KNN系列是一個(gè)非常豐富且有意思的內(nèi)容,還有很多有待我們?nèi)ヌ剿鳌:芏嗨惴ǎ鋵?shí)學(xué)的是思想,如果認(rèn)真的徹底搞清楚幾個(gè)算法的原理,你會(huì)瞬間覺得,學(xué)其他算法也簡(jiǎn)單起來,如果你沒有深刻的學(xué)過幾個(gè)算法,總覺得學(xué)啥都是朦朦朧朧,似懂非懂的,好像什么都會(huì)了,好像又啥都不會(huì)。
思考題:KNN是不是也可以做個(gè)KNN森林,如果可以,怎么做,如果不行,為什么?看完本文來做這個(gè)思考題。
