黄色片国产精品,国产大鸡吧在线观看,日韩高清无码三级,国产一级a毛一级a毛片视频黑人 ,色色色欧美,97亚洲综合影院,久久澡狠l澡欧美老妇,做爱无码在线

?Datawhale干貨?

譯者：鄭沛，英國曼徹斯特大? 來源：數(shù)據(jù)派THU

支持向量機(jī)（SVM）是每位機(jī)器學(xué)習(xí)專家都應(yīng)該在自己的知識庫中儲備的一種簡單的算法。支持向量機(jī)（SVM）受到很多人的高度青睞，因?yàn)樗枰^少的計(jì)算量，但數(shù)據(jù)準(zhǔn)確度相當(dāng)不錯(cuò)，并且可以用于回歸和分類任務(wù)。

支持向量機(jī)（SVM）介紹
支持向量機(jī)（SVM）是怎么工作的
處理異常值
PEGASOS法
非線性回歸分類
支持向量機(jī)（SVM）的優(yōu)劣
可視化支持向量機(jī)（SVM）
支持向量機(jī)（SVM）的應(yīng)用

支持向量機(jī)（SVM）介紹支持向量機(jī)（SVM）是功能強(qiáng)大的分類器，可同時(shí)處理線性和非線性數(shù)據(jù)。如果是n維空間，則超平面的維數(shù)將為（n-1）。

（左圖：在R2超平面的一根線；右圖：在R3超平面的一個(gè)平面）

支持向量機(jī)（SVM）的目標(biāo)是找到一個(gè)最佳的超平面來劃分我們的數(shù)據(jù)，從而使一個(gè)空間最近點(diǎn)到它自己的距離最大。

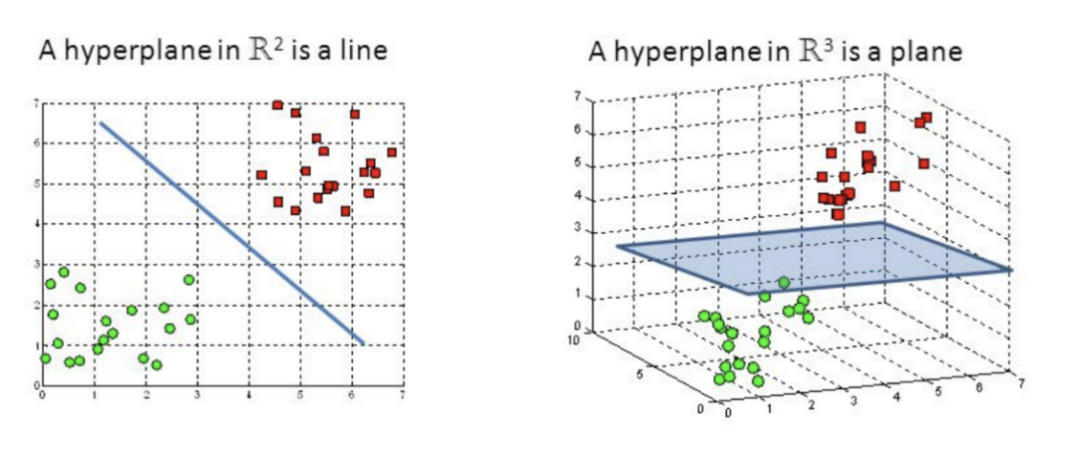
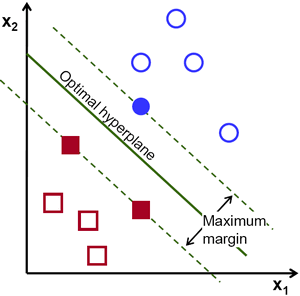
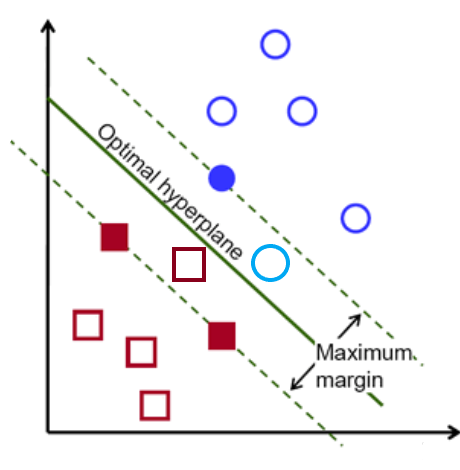
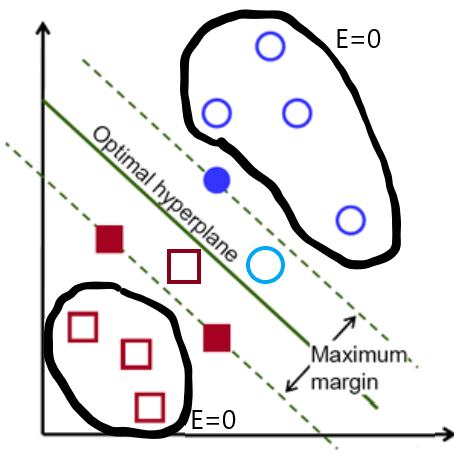
（上圖注釋：最優(yōu)超平面：Optimal hyperpline；最大間隔：Maximum margin）

簡單說，考慮一條道路，它將左右兩側(cè)的汽車、建筑物和行人分開，并盡可能使車道最寬。那么，那些真正靠近道路的那些汽車、建筑物就是支持向量。

這解釋了SVM是如何工作的。

支持向量機(jī)（SVM）是如何工作的？

目標(biāo)：找到最佳的超平面

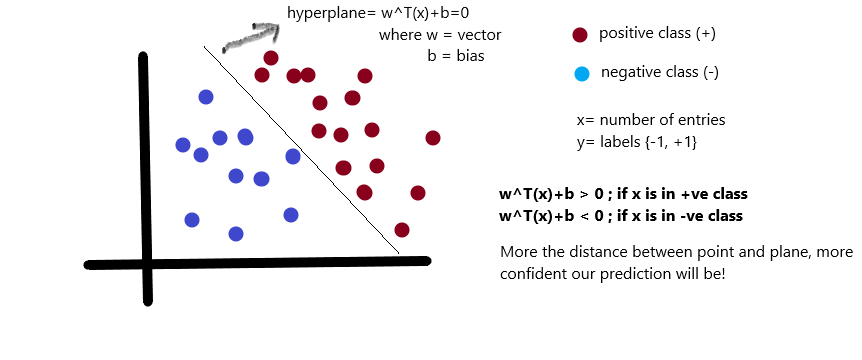
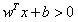（上圖注釋：我們把數(shù)據(jù)分為兩類（正類positive class和負(fù)類negative class），x為數(shù)據(jù)，y為數(shù)據(jù)的標(biāo)簽，和類別對應(yīng)；由圖中看很明顯啦，

是正的，反之是負(fù)的。由于我們需要找到所謂的“最近距離”的支持向量，那么肯定點(diǎn)越多越好了，因?yàn)檫@樣提供距離的點(diǎn)越多，就越準(zhǔn)確）

計(jì)算點(diǎn)與支持向量的距離

上圖注釋：距離怎么來的呢，高中立體幾何學(xué)過點(diǎn)到直線距離（的自然高維推廣），一種更常見的寫法是：

我們想要一個(gè)超平面，它可以很高效地對點(diǎn)進(jìn)行分類，也就是，很精確的賦予類別。

為了能夠精確地執(zhí)行這一操作，我們需要稍微變一下我們目標(biāo)。

更改目標(biāo)：

為了最大化與超平面的最小距離：

那我們先假設(shè)最小臨界距離為Y

因?yàn)楝F(xiàn)在所有的點(diǎn)都滿足下面的兩個(gè)條件：

為了能夠?qū)崿F(xiàn)最小距離，根據(jù)最小距離的公式，因?yàn)樽顑?yōu)超平面實(shí)際上已經(jīng)存在（可以當(dāng)成常數(shù)看），我們只需要最大化分母，即我們需要最大化“w”：

上述計(jì)算過程涉及到的數(shù)學(xué)有點(diǎn)繁瑣和麻煩，因此，為了減少數(shù)學(xué)上的復(fù)雜性，我們將方程式重構(gòu)（注意，y的取值范圍是

，

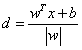
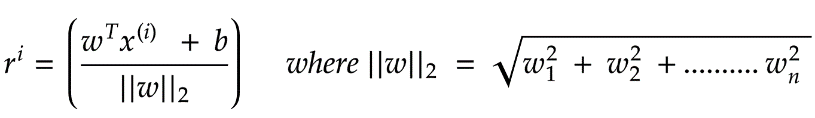
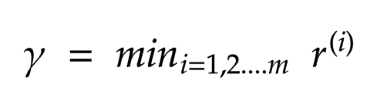
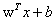為函數(shù)間隔，結(jié)合兩者同號我們可以寫成

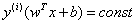形式，最大化距離則意味著

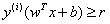，因?yàn)槲覀兊哪繕?biāo)也是最大化r）。因此，我們將以支持向量必須位于超平面上的方式對數(shù)據(jù)重新正則化。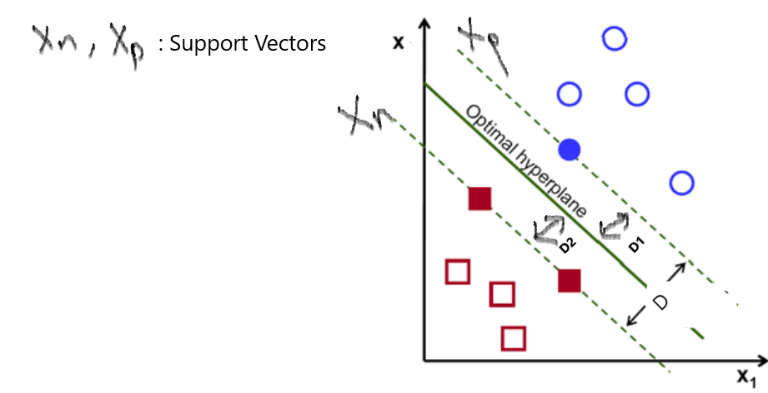

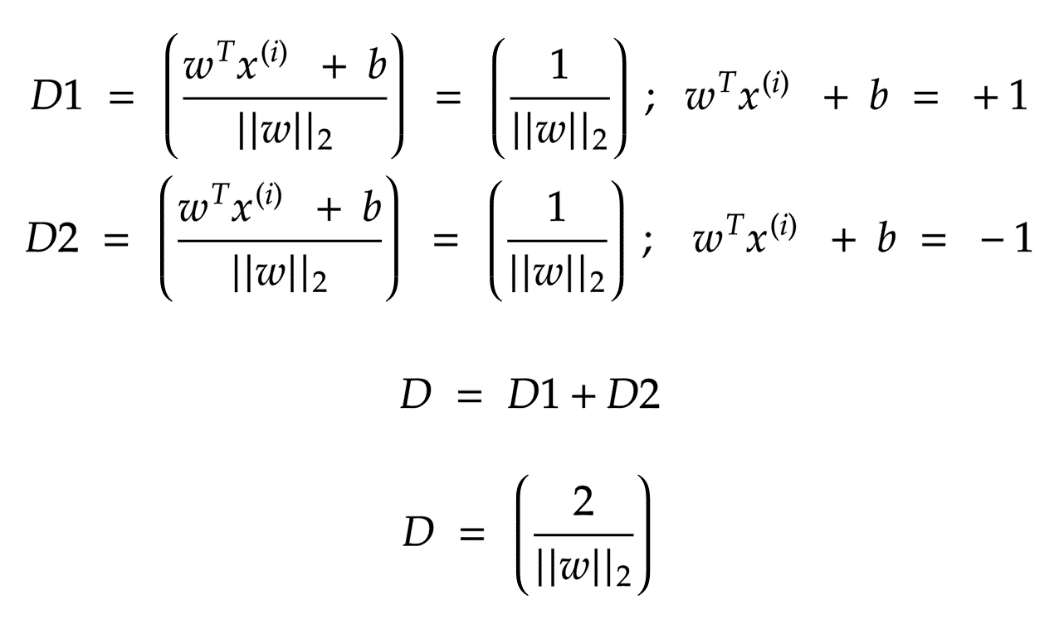
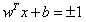因此, 為了能夠最大化“w”，我們需要最大化?“D”.

D = D1+D2；因此我們需要最大化D1和D2.（第一類為D1，第二類為D2，加到一起）

現(xiàn)在，為了增加“ D”，我們必須集中精力在最小距離必須為1（

）的情況下減少“ || w ||”。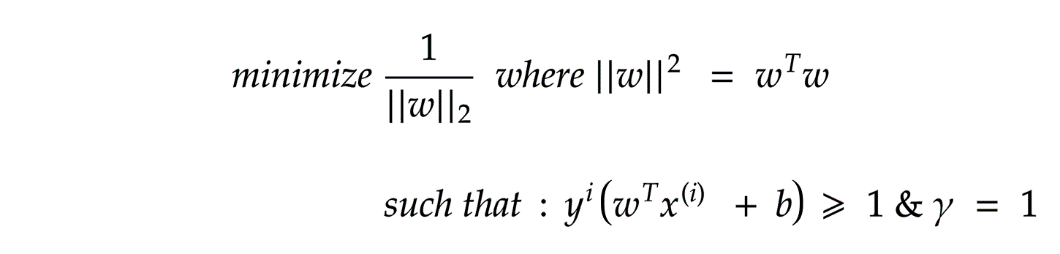

在我們的新目標(biāo)中，我們需要降低||w|| ，但是需要注意的是||w|| 不是隨意變化的，它取決于?γ。

因?yàn)椤皐“的大小取決于?γ，我們不能夠得到全局極小值。

因此我們可以得出SVM是約束凸優(yōu)化問題。

因?yàn)镾VM依賴約束，其無法使用梯度下降法，我們需要采取其他的方法。

這一問題可以采用如下措施進(jìn)行規(guī)避：

二次方程求解器
拉格朗日量密度
PEGASOS算法

處理異常值

有時(shí)對于某些示例(x(i), y(i))我們可能會遇到誤差E（i）。

誤差會破壞我們的目標(biāo)，因?yàn)樵黾诱`差會增加損失成本，但是要開發(fā)可靠的模型，我們需要允許一些誤差，否則將導(dǎo)致過擬合。為了使誤差保持在最低水平，我們將引入懲罰（penalty），一旦我們的模型錯(cuò)誤地對數(shù)據(jù)點(diǎn)進(jìn)行分類，它將面臨一定的懲罰（c），這將有助于我們提高準(zhǔn)確性。

如果 E=0 ; 那么將不會引入懲罰。于是得到下式：

如果c很大，那么差額就會越小，分類就會越準(zhǔn)確（更容易出現(xiàn)過擬合）。

如果c很小，那個(gè)差額就會越大，代價(jià)則是錯(cuò)誤的分類（更好的分類器）。

PEGASOS

為了克服約束凸優(yōu)化問題，我們采用PEGASOS方法。

我們重新制定方程式以實(shí)現(xiàn)約束獨(dú)立性

現(xiàn)在，我們進(jìn)行數(shù)學(xué)討論，因?yàn)槲覀儗⑵湎嗉右淮危窒鄿p一次，方程中的1對整體沒有影響。

為了簡化我們的方程式，我們將代入t(i)。

上式表示，如果點(diǎn)遠(yuǎn)離超平面，則誤差將為零，否則遇到的誤差將為(1-t(i))。

公式函數(shù)在t≥1時(shí)仍然沒有微分；因此我們將梯度分為子梯度1和子梯度2。

我們需要最小化的最終函數(shù)是：

現(xiàn)在，由于消除了約束，并且我們的函數(shù)與γ無關(guān)。我們可以采用梯度下降來最大程度地減少損失。

使用梯度下降將損失降至最低

計(jì)算損失

為SVM實(shí)施梯度下降

非線性分類

若使用支持向量機(jī)對非線性數(shù)據(jù)進(jìn)行分類，我們需要將數(shù)據(jù)投影到更高的維度，即通過增加2D數(shù)據(jù)特征的功能將其轉(zhuǎn)換為3D數(shù)據(jù)。

特征的增加將增加計(jì)算開銷。為了轉(zhuǎn)換數(shù)據(jù)的維度，我們將使用核（Kernel）。

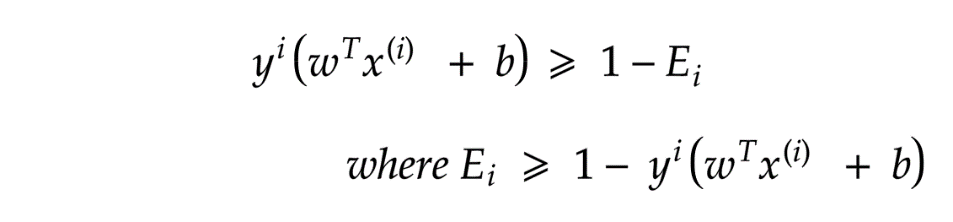
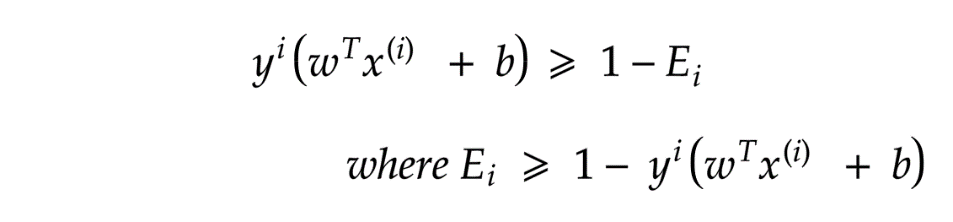
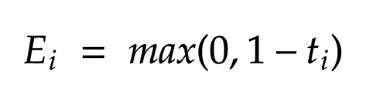
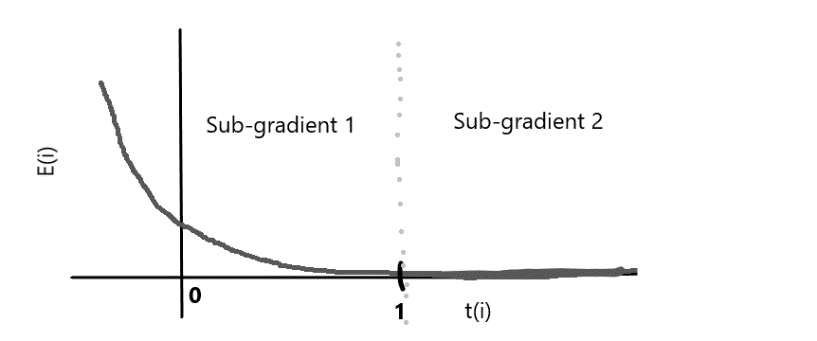
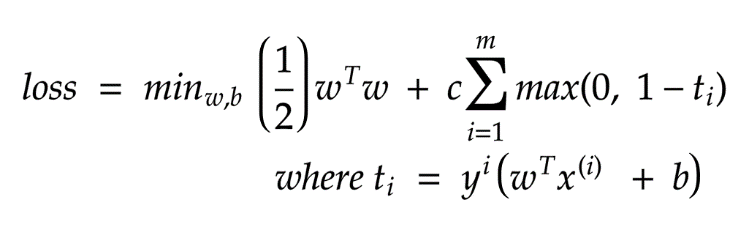
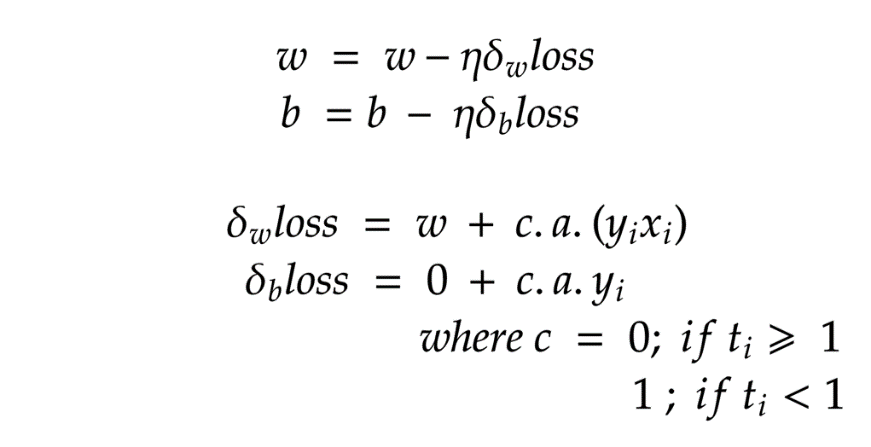
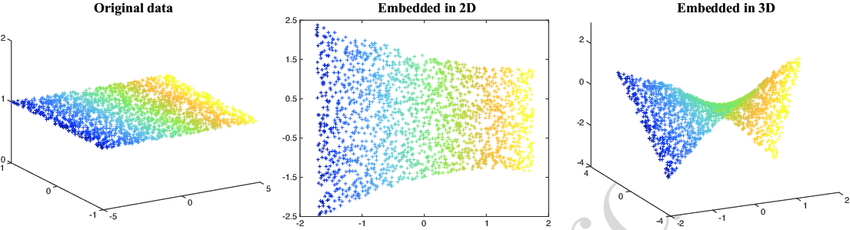
線性核
RBF（徑向基）核

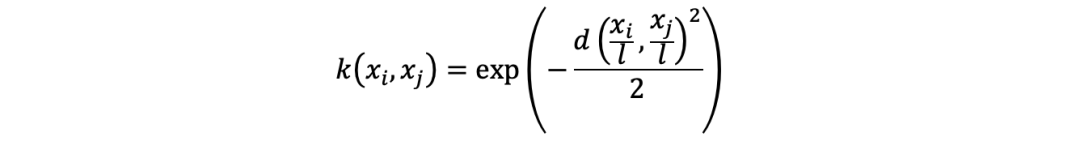
多項(xiàng)式核

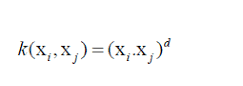
Sigmoid核

使用核技巧的障礙是為模型選擇合適的核，因?yàn)槲覀冇肋h(yuǎn)不知道哪個(gè)核最適合我們的模型，以及代價(jià)有多大。

因此為了自動調(diào)節(jié)模型中超參數(shù)，我們將采用網(wǎng)格搜索（GridSearch）法。

我們將指定參數(shù)，參數(shù)在腳本里即為由字典組成的列表（舉例如下），其中包含鍵（如內(nèi)核和懲罰），我們將針對每個(gè)核運(yùn)行模型來讓模型準(zhǔn)確率最高。

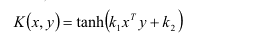
params= [{‘kernel’:[‘linear’, ‘rbf’, ‘poly’, ‘sigmoid’], ‘c’:[0.1, 0.2, 0.5, 1.0, 2.0, 5.0]}

現(xiàn)在，對于每種類型的核和5種懲罰類型，我們將存儲準(zhǔn)確率，稍后將選擇準(zhǔn)確率最高的內(nèi)核和懲罰（c）。

接受參數(shù):

cv: 交叉驗(yàn)證（cross-validation）
n_jobs: 可用的CPU數(shù)量

支持向量機(jī)的優(yōu)劣

優(yōu)勢

可以輕松處理大型特征空間
核技巧是支持向量機(jī)的真正優(yōu)勢，因?yàn)樗兄谡业缴踔粮鼜?fù)雜問題的解決方案
適用于線性和非線性數(shù)據(jù)
不容易出現(xiàn)過擬合的現(xiàn)象
甚至適用于非結(jié)構(gòu)化數(shù)據(jù)

劣勢

對噪音敏感
選擇最佳核比較困難
大型數(shù)據(jù)集的訓(xùn)練時(shí)間長

可視化支持向量機(jī)

支持向量機(jī)的應(yīng)用

“干貨學(xué)習(xí)，點(diǎn)贊三連↓

支持向量機(jī)背后的數(shù)學(xué)原理！