從一場(chǎng)相親說(shuō)起，決策樹(shù)

大家好，我是 Jack。

今天，聊聊決策樹(shù)，讓我們從一場(chǎng)相親開(kāi)始說(shuō)起。

決策樹(shù)的定義

決策樹(shù)是什么？決策樹(shù)(decision tree)是一種基本的分類(lèi)與回歸方法。

舉個(gè)通俗易懂的例子，如下圖所示的流程圖就是一個(gè)決策樹(shù)，長(zhǎng)方形代表判斷模塊(decision block)，橢圓形成代表終止模塊(terminating block)，表示已經(jīng)得出結(jié)論，可以終止運(yùn)行。

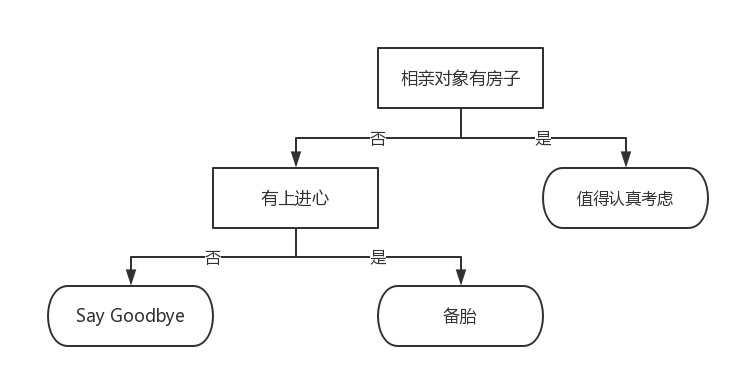
從判斷模塊引出的左右箭頭稱(chēng)作為分支(branch)，它可以達(dá)到另一個(gè)判斷模塊或者終止模塊。我們還可以這樣理解，分類(lèi)決策樹(shù)模型是一種描述對(duì)實(shí)例進(jìn)行分類(lèi)的樹(shù)形結(jié)構(gòu)。

決策樹(shù)由結(jié)點(diǎn)(node)和有向邊(directed edge)組成。結(jié)點(diǎn)有兩種類(lèi)型：內(nèi)部結(jié)點(diǎn)(internal node)和葉結(jié)點(diǎn)(leaf node)。

內(nèi)部結(jié)點(diǎn)表示一個(gè)特征或?qū)傩裕~結(jié)點(diǎn)表示一個(gè)類(lèi)。

蒙圈沒(méi)？？長(zhǎng)方形和橢圓形都是結(jié)點(diǎn)。長(zhǎng)方形的結(jié)點(diǎn)屬于內(nèi)部結(jié)點(diǎn)，橢圓形的結(jié)點(diǎn)屬于葉結(jié)點(diǎn)，從結(jié)點(diǎn)引出的左右箭頭就是有向邊。而最上面的結(jié)點(diǎn)就是決策樹(shù)的根結(jié)點(diǎn)(root node)。

這樣，結(jié)點(diǎn)說(shuō)法就與模塊說(shuō)法對(duì)應(yīng)上了，理解就好。

我們回到這個(gè)流程圖，對(duì)，你沒(méi)看錯(cuò)，這就是一個(gè)假想的相親對(duì)象分類(lèi)系統(tǒng)。

它首先檢測(cè)相親對(duì)方是否有房。如果有房，則對(duì)于這個(gè)相親對(duì)象可以考慮進(jìn)一步接觸。

如果沒(méi)有房，則觀(guān)察相親對(duì)象是否有上進(jìn)心，如果沒(méi)有，直接Say Goodbye，此時(shí)可以說(shuō)："你人很好，但是我們不合適。"

如果有，則可以把這個(gè)相親對(duì)象列入候選名單，好聽(tīng)點(diǎn)叫候選名單，有點(diǎn)瑕疵地講，那就是備胎。

不過(guò)這只是個(gè)簡(jiǎn)單的相親對(duì)象分類(lèi)系統(tǒng)，只是做了簡(jiǎn)單的分類(lèi)。真實(shí)情況可能要復(fù)雜得多，考慮因素也可以是五花八門(mén)。

脾氣好嗎？會(huì)做飯嗎？愿意做家務(wù)嗎？家里幾個(gè)孩子？父母是干什么的？

我們可以把決策樹(shù)看成一個(gè)if-then規(guī)則的集合，將決策樹(shù)轉(zhuǎn)換成if-then規(guī)則的過(guò)程是這樣的：由決策樹(shù)的根結(jié)點(diǎn)(root node)到葉結(jié)點(diǎn)(leaf node)的每一條路徑構(gòu)建一條規(guī)則；路徑上內(nèi)部結(jié)點(diǎn)的特征對(duì)應(yīng)著規(guī)則的條件，而葉結(jié)點(diǎn)的類(lèi)對(duì)應(yīng)著規(guī)則的結(jié)論。

決策樹(shù)的路徑或其對(duì)應(yīng)的if-then規(guī)則集合具有一個(gè)重要的性質(zhì)：互斥并且完備。這就是說(shuō)，每一個(gè)實(shí)例都被一條路徑或一條規(guī)則所覆蓋，而且只被一條路徑或一條規(guī)則所覆蓋。這里所覆蓋是指實(shí)例的特征與路徑上的特征一致或?qū)嵗凉M(mǎn)足規(guī)則的條件。

使用決策樹(shù)做預(yù)測(cè)需要以下過(guò)程：

• 收集數(shù)據(jù)：可以使用任何方法。比如想構(gòu)建一個(gè)相親系統(tǒng)，我們可以從媒婆那里，或者通過(guò)采訪(fǎng)相親對(duì)象獲取數(shù)據(jù)。根據(jù)他們考慮的因素和最終的選擇結(jié)果，就可以得到一些供我們利用的數(shù)據(jù)了。
• 準(zhǔn)備數(shù)據(jù)：收集完的數(shù)據(jù)，我們要進(jìn)行整理，將這些所有收集的信息按照一定規(guī)則整理出來(lái)，并排版，方便我們進(jìn)行后續(xù)處理。
• 分析數(shù)據(jù)：可以使用任何方法，決策樹(shù)構(gòu)造完成之后，我們可以檢查決策樹(shù)圖形是否符合預(yù)期。
• 訓(xùn)練算法：這個(gè)過(guò)程也就是構(gòu)造決策樹(shù)，同樣也可以說(shuō)是決策樹(shù)學(xué)習(xí)，就是構(gòu)造一個(gè)決策樹(shù)的數(shù)據(jù)結(jié)構(gòu)。
• 測(cè)試算法：使用經(jīng)驗(yàn)樹(shù)計(jì)算錯(cuò)誤率。當(dāng)錯(cuò)誤率達(dá)到了可接收范圍，這個(gè)決策樹(shù)就可以投放使用了。
• 使用算法：此步驟可以使用適用于任何監(jiān)督學(xué)習(xí)算法，而使用決策樹(shù)可以更好地理解數(shù)據(jù)的內(nèi)在含義。

構(gòu)建決策樹(shù)

使用決策樹(shù)做預(yù)測(cè)的每一步驟都很重要，數(shù)據(jù)收集不到位，將會(huì)導(dǎo)致沒(méi)有足夠的特征讓我們構(gòu)建錯(cuò)誤率低的決策樹(shù)。數(shù)據(jù)特征充足，但是不知道用哪些特征好，將會(huì)導(dǎo)致無(wú)法構(gòu)建出分類(lèi)效果好的決策樹(shù)模型。從算法方面看，決策樹(shù)的構(gòu)建是我們的核心內(nèi)容。

決策樹(shù)要如何構(gòu)建呢？通常，這一過(guò)程可以概括為3個(gè)步驟：特征選擇、決策樹(shù)的生成和決策樹(shù)的修剪。

1、特征選擇

特征選擇在于選取對(duì)訓(xùn)練數(shù)據(jù)具有分類(lèi)能力的特征。這樣可以提高決策樹(shù)學(xué)習(xí)的效率，如果利用一個(gè)特征進(jìn)行分類(lèi)的結(jié)果與隨機(jī)分類(lèi)的結(jié)果沒(méi)有很大差別，則稱(chēng)這個(gè)特征是沒(méi)有分類(lèi)能力的。經(jīng)驗(yàn)上扔掉這樣的特征對(duì)決策樹(shù)學(xué)習(xí)的精度影響不大。

通常特征選擇的標(biāo)準(zhǔn)是信息增益(information gain)或信息增益比，為了簡(jiǎn)單，本文使用信息增益作為選擇特征的標(biāo)準(zhǔn)。那么，什么是信息增益？在講解信息增益之前，讓我們看一組實(shí)例，貸款申請(qǐng)樣本數(shù)據(jù)表。

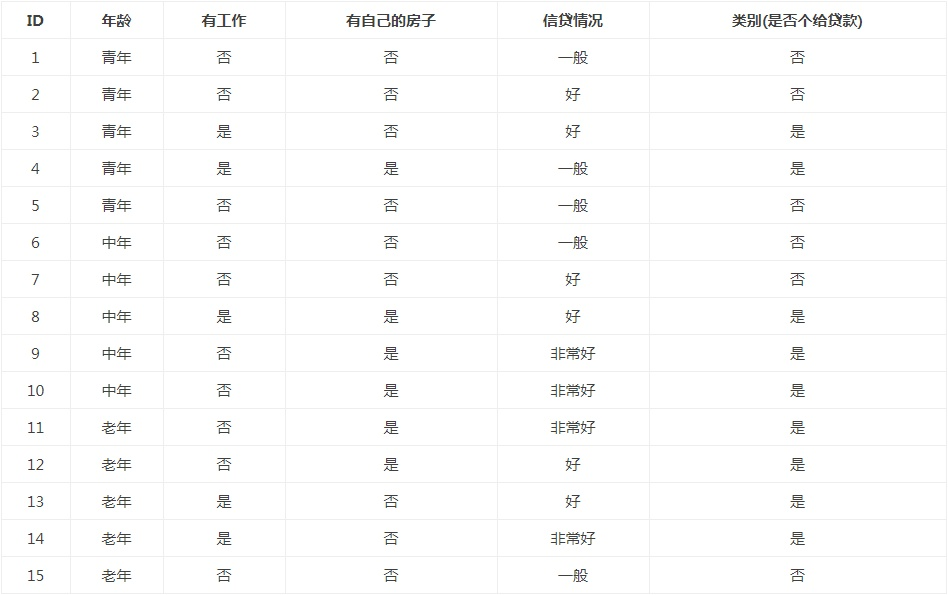
希望通過(guò)所給的訓(xùn)練數(shù)據(jù)學(xué)習(xí)一個(gè)貸款申請(qǐng)的決策樹(shù)，用于對(duì)未來(lái)的貸款申請(qǐng)進(jìn)行分類(lèi)，即當(dāng)新的客戶(hù)提出貸款申請(qǐng)時(shí)，根據(jù)申請(qǐng)人的特征利用決策樹(shù)決定是否批準(zhǔn)貸款申請(qǐng)。

特征選擇就是決定用哪個(gè)特征來(lái)劃分特征空間。比如，我們通過(guò)上述數(shù)據(jù)表得到兩個(gè)可能的決策樹(shù)，分別由兩個(gè)不同特征的根結(jié)點(diǎn)構(gòu)成。

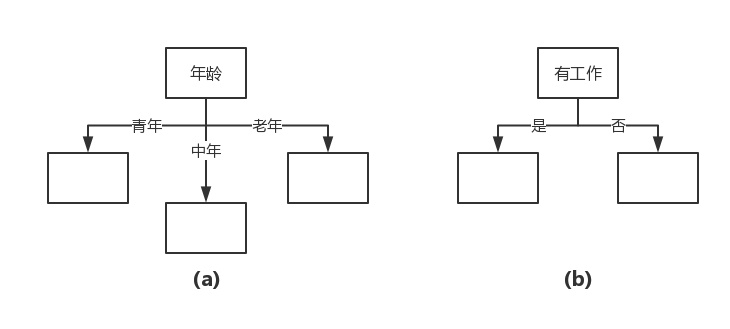
圖(a)所示的根結(jié)點(diǎn)的特征是年齡，有3個(gè)取值，對(duì)應(yīng)于不同的取值有不同的子結(jié)點(diǎn)。圖(b)所示的根節(jié)點(diǎn)的特征是工作，有2個(gè)取值，對(duì)應(yīng)于不同的取值有不同的子結(jié)點(diǎn)。兩個(gè)決策樹(shù)都可以從此延續(xù)下去。

問(wèn)題是：究竟選擇哪個(gè)特征更好些？這就要求確定選擇特征的準(zhǔn)則。直觀(guān)上，如果一個(gè)特征具有更好的分類(lèi)能力，或者說(shuō)，按照這一特征將訓(xùn)練數(shù)據(jù)集分割成子集，使得各個(gè)子集在當(dāng)前條件下有最好的分類(lèi)，那么就更應(yīng)該選擇這個(gè)特征。信息增益就能夠很好地表示這一直觀(guān)的準(zhǔn)則。

什么是信息增益呢？在劃分?jǐn)?shù)據(jù)集之后信息發(fā)生的變化稱(chēng)為信息增益，知道如何計(jì)算信息增益，我們就可以計(jì)算每個(gè)特征值劃分?jǐn)?shù)據(jù)集獲得的信息增益，獲得信息增益最高的特征就是最好的選擇。

（1）香農(nóng)熵

在可以評(píng)測(cè)哪個(gè)數(shù)據(jù)劃分方式是最好的數(shù)據(jù)劃分之前，我們必須學(xué)習(xí)如何計(jì)算信息增益。集合信息的度量方式稱(chēng)為香農(nóng)熵或者簡(jiǎn)稱(chēng)為熵(entropy)，這個(gè)名字來(lái)源于信息論之父克勞德·香農(nóng)。

如果看不明白什么是信息增益和熵，請(qǐng)不要著急，因?yàn)樗麄冏哉Q生的那一天起，就注定會(huì)令世人十分費(fèi)解。克勞德·香農(nóng)寫(xiě)完信息論之后，約翰·馮·諾依曼建議使用"熵"這個(gè)術(shù)語(yǔ)，因?yàn)榇蠹叶疾恢浪鞘裁匆馑肌?/p>

熵定義為信息的期望值。在信息論與概率統(tǒng)計(jì)中，熵是表示隨機(jī)變量不確定性的度量。如果待分類(lèi)的事物可能劃分在多個(gè)分類(lèi)之中，則符號(hào)xi的信息定義為 ：

其中p(xi)是選擇該分類(lèi)的概率。有人可能會(huì)問(wèn)，信息為啥這樣定義啊？答曰：前輩得出的結(jié)論。這就跟1+1等于2一樣，記住并且會(huì)用即可。上述式中的對(duì)數(shù)以2為底，也可以e為底(自然對(duì)數(shù))。

通過(guò)上式，我們可以得到所有類(lèi)別的信息。為了計(jì)算熵，我們需要計(jì)算所有類(lèi)別所有可能值包含的信息期望值(數(shù)學(xué)期望)，通過(guò)下面的公式得到：

其中n是分類(lèi)的數(shù)目。熵越大，隨機(jī)變量的不確定性就越大。

當(dāng)熵中的概率由數(shù)據(jù)估計(jì)(特別是最大似然估計(jì))得到時(shí)，所對(duì)應(yīng)的熵稱(chēng)為經(jīng)驗(yàn)熵(empirical entropy)。什么叫由數(shù)據(jù)估計(jì)？比如有10個(gè)數(shù)據(jù)，一共有兩個(gè)類(lèi)別，A類(lèi)和B類(lèi)。其中有7個(gè)數(shù)據(jù)屬于A類(lèi)，則該A類(lèi)的概率即為十分之七。其中有3個(gè)數(shù)據(jù)屬于B類(lèi)，則該B類(lèi)的概率即為十分之三。

淺顯的解釋就是，這概率是我們根據(jù)數(shù)據(jù)數(shù)出來(lái)的。我們定義貸款申請(qǐng)樣本數(shù)據(jù)表中的數(shù)據(jù)為訓(xùn)練數(shù)據(jù)集D，則訓(xùn)練數(shù)據(jù)集D的經(jīng)驗(yàn)熵為H(D)，|D|表示其樣本容量，及樣本個(gè)數(shù)。

設(shè)有K個(gè)類(lèi)Ck, = 1,2,3,...,K,|Ck|為屬于類(lèi)Ck的樣本個(gè)數(shù)，因此經(jīng)驗(yàn)熵公式就可以寫(xiě)為 ：

根據(jù)此公式計(jì)算經(jīng)驗(yàn)熵H(D)，分析貸款申請(qǐng)樣本數(shù)據(jù)表中的數(shù)據(jù)。最終分類(lèi)結(jié)果只有兩類(lèi)，即放貸和不放貸。根據(jù)表中的數(shù)據(jù)統(tǒng)計(jì)可知，在15個(gè)數(shù)據(jù)中，9個(gè)數(shù)據(jù)的結(jié)果為放貸，6個(gè)數(shù)據(jù)的結(jié)果為不放貸。所以數(shù)據(jù)集D的經(jīng)驗(yàn)熵H(D)為：

經(jīng)過(guò)計(jì)算可知，數(shù)據(jù)集D的經(jīng)驗(yàn)熵H(D)的值為0.971。

（2）編寫(xiě)代碼計(jì)算經(jīng)驗(yàn)熵

在編寫(xiě)代碼之前，我們先對(duì)數(shù)據(jù)集進(jìn)行屬性標(biāo)注。

• 年齡：0代表青年，1代表中年，2代表老年；
• 有工作：0代表否，1代表是；
• 有自己的房子：0代表否，1代表是；
• 信貸情況：0代表一般，1代表好，2代表非常好；
• 類(lèi)別(是否給貸款)：no代表否，yes代表是。

確定這些之后，我們就可以創(chuàng)建數(shù)據(jù)集，并計(jì)算經(jīng)驗(yàn)熵了，代碼編寫(xiě)如下：

# -*- coding: UTF-8 -*-
from math import log

"""
函數(shù)說(shuō)明:創(chuàng)建測(cè)試數(shù)據(jù)集

Parameters:
    無(wú)
Returns:
    dataSet - 數(shù)據(jù)集
    labels - 分類(lèi)屬性
Author:
    Jack Cui
"""
def createDataSet():
    dataSet = [[0, 0, 0, 0, 'no'],         #數(shù)據(jù)集
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    labels = ['不放貸', '放貸']             #分類(lèi)屬性
    return dataSet, labels                #返回?cái)?shù)據(jù)集和分類(lèi)屬性

"""
函數(shù)說(shuō)明:計(jì)算給定數(shù)據(jù)集的經(jīng)驗(yàn)熵(香農(nóng)熵)

Parameters:
    dataSet - 數(shù)據(jù)集
Returns:
    shannonEnt - 經(jīng)驗(yàn)熵(香農(nóng)熵)
Author:
    Jack Cui
Modify:
    2017-03-29
"""
def calcShannonEnt(dataSet):
    numEntires = len(dataSet)                        #返回?cái)?shù)據(jù)集的行數(shù)
    labelCounts = {}                                #保存每個(gè)標(biāo)簽(Label)出現(xiàn)次數(shù)的字典
    for featVec in dataSet:                            #對(duì)每組特征向量進(jìn)行統(tǒng)計(jì)
        currentLabel = featVec[-1]                    #提取標(biāo)簽(Label)信息
        if currentLabel not in labelCounts.keys():    #如果標(biāo)簽(Label)沒(méi)有放入統(tǒng)計(jì)次數(shù)的字典,添加進(jìn)去
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1                #Label計(jì)數(shù)
    shannonEnt = 0.0                                #經(jīng)驗(yàn)熵(香農(nóng)熵)
    for key in labelCounts:                            #計(jì)算香農(nóng)熵
        prob = float(labelCounts[key]) / numEntires    #選擇該標(biāo)簽(Label)的概率
        shannonEnt -= prob * log(prob, 2)            #利用公式計(jì)算
    return shannonEnt                                #返回經(jīng)驗(yàn)熵(香農(nóng)熵)

if __name__ == '__main__':
    dataSet, features = createDataSet()
    print(dataSet)
    print(calcShannonEnt(dataSet))

代碼運(yùn)行結(jié)果如下圖所示，代碼是先打印訓(xùn)練數(shù)據(jù)集，然后打印計(jì)算的經(jīng)驗(yàn)熵H(D)，程序計(jì)算的結(jié)果與我們統(tǒng)計(jì)計(jì)算的結(jié)果是一致的，程序沒(méi)有問(wèn)題。

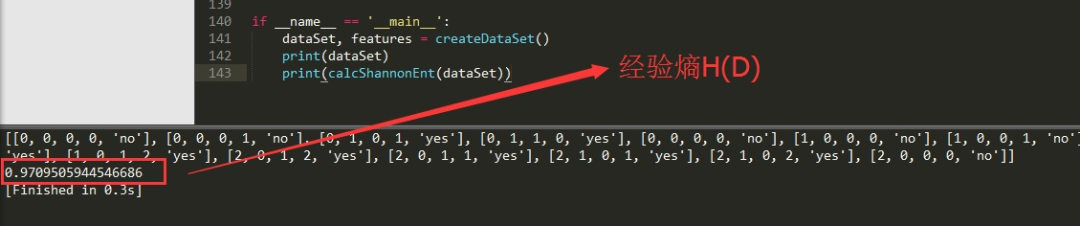
（3） 信息增益

在上面，我們已經(jīng)說(shuō)過(guò)，如何選擇特征，需要看信息增益。也就是說(shuō)，信息增益是相對(duì)于特征而言的，信息增益越大，特征對(duì)最終的分類(lèi)結(jié)果影響也就越大，我們就應(yīng)該選擇對(duì)最終分類(lèi)結(jié)果影響最大的那個(gè)特征作為我們的分類(lèi)特征。

在講解信息增益定義之前，我們還需要明確一個(gè)概念，條件熵。

熵我們知道是什么，條件熵又是個(gè)什么鬼？條件熵H(Y|X)表示在已知隨機(jī)變量X的條件下隨機(jī)變量Y的不確定性，隨機(jī)變量X給定的條件下隨機(jī)變量Y的條件熵(conditional entropy)H(Y|X)，定義為X給定條件下Y的條件概率分布的熵對(duì)X的數(shù)學(xué)期望：

這里，

同理，當(dāng)條件熵中的概率由數(shù)據(jù)估計(jì)(特別是極大似然估計(jì))得到時(shí)，所對(duì)應(yīng)的條件熵稱(chēng)為條件經(jīng)驗(yàn)熵(empirical conditional entropy)。

明確了條件熵和經(jīng)驗(yàn)條件熵的概念。接下來(lái)，讓我們說(shuō)說(shuō)信息增益。前面也提到了，信息增益是相對(duì)于特征而言的。所以，特征A對(duì)訓(xùn)練數(shù)據(jù)集D的信息增益g(D,A)，定義為集合D的經(jīng)驗(yàn)熵H(D)與特征A給定條件下D的經(jīng)驗(yàn)條件熵H(D|A)之差，即：

一般地，熵H(D)與條件熵H(D|A)之差稱(chēng)為互信息(mutual information)。決策樹(shù)學(xué)習(xí)中的信息增益等價(jià)于訓(xùn)練數(shù)據(jù)集中類(lèi)與特征的互信息。

設(shè)特征A有n個(gè)不同的取值{a1,a2,···,an}，根據(jù)特征A的取值將D劃分為n個(gè)子集{D1,D2，···,Dn}，|Di|為Di的樣本個(gè)數(shù)。記子集Di中屬于Ck的樣本的集合為Dik，即Dik = Di ∩ Ck，|Dik|為Dik的樣本個(gè)數(shù)。于是經(jīng)驗(yàn)條件熵的公式可以些為：

說(shuō)了這么多概念性的東西，沒(méi)有聽(tīng)懂也沒(méi)有關(guān)系，舉幾個(gè)例子，再回來(lái)看一下概念，就懂了。

以貸款申請(qǐng)樣本數(shù)據(jù)表為例進(jìn)行說(shuō)明。看下年齡這一列的數(shù)據(jù)，也就是特征A1，一共有三個(gè)類(lèi)別，分別是：青年、中年和老年。我們只看年齡是青年的數(shù)據(jù)，年齡是青年的數(shù)據(jù)一共有5個(gè)，所以年齡是青年的數(shù)據(jù)在訓(xùn)練數(shù)據(jù)集出現(xiàn)的概率是十五分之五，也就是三分之一。同理，年齡是中年和老年的數(shù)據(jù)在訓(xùn)練數(shù)據(jù)集出現(xiàn)的概率也都是三分之一。

現(xiàn)在我們只看年齡是青年的數(shù)據(jù)的最終得到貸款的概率為五分之二，因?yàn)樵谖鍌€(gè)數(shù)據(jù)中，只有兩個(gè)數(shù)據(jù)顯示拿到了最終的貸款，同理，年齡是中年和老年的數(shù)據(jù)最終得到貸款的概率分別為五分之三、五分之四。所以計(jì)算年齡的信息增益，過(guò)程如下：

同理，計(jì)算其余特征的信息增益g(D,A2)、g(D,A3)和g(D,A4)。分別為：

最后，比較特征的信息增益，由于特征A3(有自己的房子)的信息增益值最大，所以選擇A3作為最優(yōu)特征。

（4） 編寫(xiě)代碼計(jì)算信息增益

我們已經(jīng)學(xué)會(huì)了通過(guò)公式計(jì)算信息增益，接下來(lái)編寫(xiě)代碼，計(jì)算信息增益。

# -*- coding: UTF-8 -*-
from math import log

"""
函數(shù)說(shuō)明:計(jì)算給定數(shù)據(jù)集的經(jīng)驗(yàn)熵(香農(nóng)熵)

Parameters:
    dataSet - 數(shù)據(jù)集
Returns:
    shannonEnt - 經(jīng)驗(yàn)熵(香農(nóng)熵)
Author:
    Jack Cui
Modify:
    2017-03-29
"""
def calcShannonEnt(dataSet):
    numEntires = len(dataSet)                        #返回?cái)?shù)據(jù)集的行數(shù)
    labelCounts = {}                                #保存每個(gè)標(biāo)簽(Label)出現(xiàn)次數(shù)的字典
    for featVec in dataSet:                            #對(duì)每組特征向量進(jìn)行統(tǒng)計(jì)
        currentLabel = featVec[-1]                    #提取標(biāo)簽(Label)信息
        if currentLabel not in labelCounts.keys():    #如果標(biāo)簽(Label)沒(méi)有放入統(tǒng)計(jì)次數(shù)的字典,添加進(jìn)去
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1                #Label計(jì)數(shù)
    shannonEnt = 0.0                                #經(jīng)驗(yàn)熵(香農(nóng)熵)
    for key in labelCounts:                            #計(jì)算香農(nóng)熵
        prob = float(labelCounts[key]) / numEntires    #選擇該標(biāo)簽(Label)的概率
        shannonEnt -= prob * log(prob, 2)            #利用公式計(jì)算
    return shannonEnt                                #返回經(jīng)驗(yàn)熵(香農(nóng)熵)

"""
函數(shù)說(shuō)明:創(chuàng)建測(cè)試數(shù)據(jù)集

Parameters:
    無(wú)
Returns:
    dataSet - 數(shù)據(jù)集
    labels - 分類(lèi)屬性
Author:
    Jack Cui
"""
def createDataSet():
    dataSet = [[0, 0, 0, 0, 'no'],                        #數(shù)據(jù)集
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    labels = ['不放貸', '放貸']            #分類(lèi)屬性
    return dataSet, labels                             #返回?cái)?shù)據(jù)集和分類(lèi)屬性

"""
函數(shù)說(shuō)明:按照給定特征劃分?jǐn)?shù)據(jù)集

Parameters:
    dataSet - 待劃分的數(shù)據(jù)集
    axis - 劃分?jǐn)?shù)據(jù)集的特征
    value - 需要返回的特征的值
Returns:
    無(wú)
Author:
    Jack Cui
"""
def splitDataSet(dataSet, axis, value):       
    retDataSet = []                                        #創(chuàng)建返回的數(shù)據(jù)集列表
    for featVec in dataSet:                             #遍歷數(shù)據(jù)集
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]                #去掉axis特征
            reducedFeatVec.extend(featVec[axis+1:])     #將符合條件的添加到返回的數(shù)據(jù)集
            retDataSet.append(reducedFeatVec)
    return retDataSet                                      #返回劃分后的數(shù)據(jù)集

"""
函數(shù)說(shuō)明:選擇最優(yōu)特征

Parameters:
    dataSet - 數(shù)據(jù)集
Returns:
    bestFeature - 信息增益最大的(最優(yōu))特征的索引值
Author:
    Jack Cui
"""
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1                    #特征數(shù)量
    baseEntropy = calcShannonEnt(dataSet)                 #計(jì)算數(shù)據(jù)集的香農(nóng)熵
    bestInfoGain = 0.0                                  #信息增益
    bestFeature = -1                                    #最優(yōu)特征的索引值
    for i in range(numFeatures):                         #遍歷所有特征
        #獲取dataSet的第i個(gè)所有特征
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)                         #創(chuàng)建set集合{},元素不可重復(fù)
        newEntropy = 0.0                                  #經(jīng)驗(yàn)條件熵
        for value in uniqueVals:                         #計(jì)算信息增益
            subDataSet = splitDataSet(dataSet, i, value)         #subDataSet劃分后的子集
            prob = len(subDataSet) / float(len(dataSet))           #計(jì)算子集的概率
            newEntropy += prob * calcShannonEnt(subDataSet)     #根據(jù)公式計(jì)算經(jīng)驗(yàn)條件熵
        infoGain = baseEntropy - newEntropy                     #信息增益
        print("第%d個(gè)特征的增益為%.3f" % (i, infoGain))            #打印每個(gè)特征的信息增益
        if (infoGain > bestInfoGain):                             #計(jì)算信息增益
            bestInfoGain = infoGain                             #更新信息增益，找到最大的信息增益
            bestFeature = i                                     #記錄信息增益最大的特征的索引值
    return bestFeature                                             #返回信息增益最大的特征的索引值

if __name__ == '__main__':
    dataSet, features = createDataSet()
    print("最優(yōu)特征索引值:" + str(chooseBestFeatureToSplit(dataSet)))

splitDataSet函數(shù)是用來(lái)選擇各個(gè)特征的子集的，比如選擇年齡(第0個(gè)特征)的青年(用0代表)的自己，我們可以調(diào)用splitDataSet(dataSet,0,0)這樣返回的子集就是年齡為青年的5個(gè)數(shù)據(jù)集。

chooseBestFeatureToSplit是選擇選擇最優(yōu)特征的函數(shù)。運(yùn)行代碼結(jié)果如下：

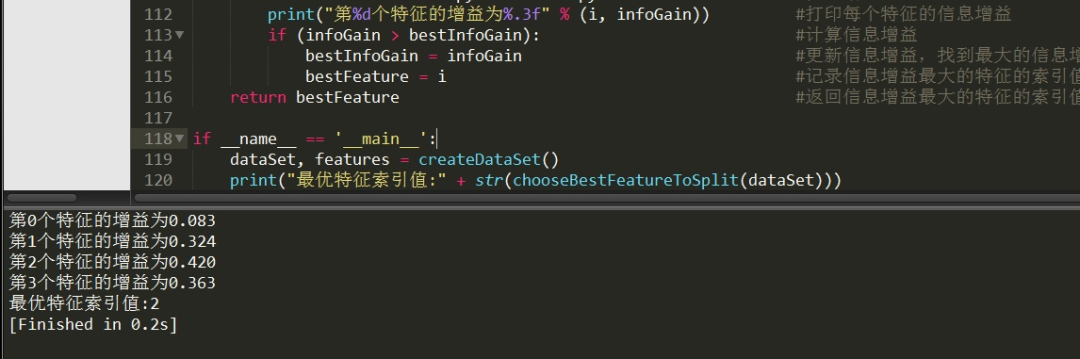
對(duì)比我們自己計(jì)算的結(jié)果，發(fā)現(xiàn)結(jié)果完全正確！最優(yōu)特征的索引值為2，也就是特征A3(有自己的房子)。

2、決策樹(shù)生成和修剪

我們已經(jīng)學(xué)習(xí)了從數(shù)據(jù)集構(gòu)造決策樹(shù)算法所需要的子功能模塊，包括經(jīng)驗(yàn)熵的計(jì)算和最優(yōu)特征的選擇，其工作原理如下：得到原始數(shù)據(jù)集，然后基于最好的屬性值劃分?jǐn)?shù)據(jù)集，由于特征值可能多于兩個(gè)，因此可能存在大于兩個(gè)分支的數(shù)據(jù)集劃分。第一次劃分之后，數(shù)據(jù)集被向下傳遞到樹(shù)的分支的下一個(gè)結(jié)點(diǎn)。在這個(gè)結(jié)點(diǎn)上，我們可以再次劃分?jǐn)?shù)據(jù)。因此我們可以采用遞歸的原則處理數(shù)據(jù)集。

構(gòu)建決策樹(shù)的算法有很多，比如C4.5、ID3和CART，這些算法在運(yùn)行時(shí)并不總是在每次劃分?jǐn)?shù)據(jù)分組時(shí)都會(huì)消耗特征。由于特征數(shù)目并不是每次劃分?jǐn)?shù)據(jù)分組時(shí)都減少，因此這些算法在實(shí)際使用時(shí)可能引起一定的問(wèn)題。

目前我們并不需要考慮這個(gè)問(wèn)題，只需要在算法開(kāi)始運(yùn)行前計(jì)算列的數(shù)目，查看算法是否使用了所有屬性即可。

決策樹(shù)生成算法遞歸地產(chǎn)生決策樹(shù)，直到不能繼續(xù)下去未為止。這樣產(chǎn)生的樹(shù)往往對(duì)訓(xùn)練數(shù)據(jù)的分類(lèi)很準(zhǔn)確，但對(duì)未知的測(cè)試數(shù)據(jù)的分類(lèi)卻沒(méi)有那么準(zhǔn)確，即出現(xiàn)過(guò)擬合現(xiàn)象。

過(guò)擬合的原因在于學(xué)習(xí)時(shí)過(guò)多地考慮如何提高對(duì)訓(xùn)練數(shù)據(jù)的正確分類(lèi)，從而構(gòu)建出過(guò)于復(fù)雜的決策樹(shù)。解決這個(gè)問(wèn)題的辦法是考慮決策樹(shù)的復(fù)雜度，對(duì)已生成的決策樹(shù)進(jìn)行簡(jiǎn)化。

總結(jié)

本篇文章講解了如何計(jì)算數(shù)據(jù)集的經(jīng)驗(yàn)熵和如何選擇最優(yōu)特征作為分類(lèi)特征。決策樹(shù)如何生成、修剪、可視化，以及整體實(shí)例練習(xí)，會(huì)在后續(xù)的文章中進(jìn)行講解。