楠哥帶你搞定MySQL索引,再也不怕面試官問了!

致力于最高效的Java學(xué)習(xí)

B 站搜索:楠哥教你學(xué)Java
獲取更多優(yōu)質(zhì)視頻教程
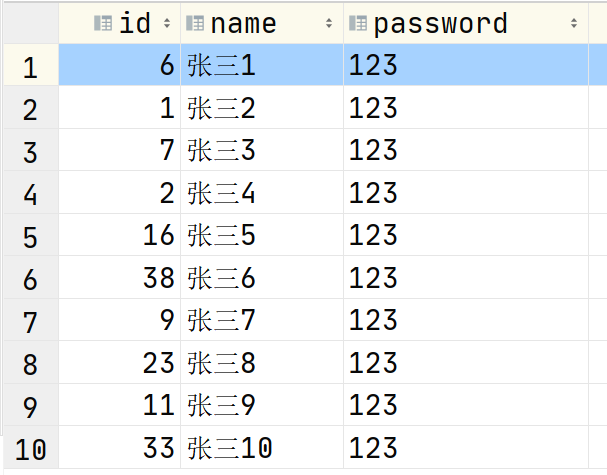
這個時候,需要逐行遍歷,直到找到 id = 11 的那行數(shù)據(jù),而 MySQL 的數(shù)據(jù)都是存儲在磁盤中的,而非緩存,所以效率就比較低,每查詢一行都要去磁盤上查找,由上圖我們可以得知,找到 id = 11 的數(shù)據(jù),需要查找 9 次,這是在沒有索引的情況下。
現(xiàn)在我們給 id 添加索引,所謂的添加索引,是指在存儲數(shù)據(jù)的同時去維護(hù)一個存儲了 id 值的數(shù)據(jù)結(jié)構(gòu),比如二叉樹,即把 id 的值存到二叉樹中,按表中的數(shù)據(jù)則會形成下列二叉樹。
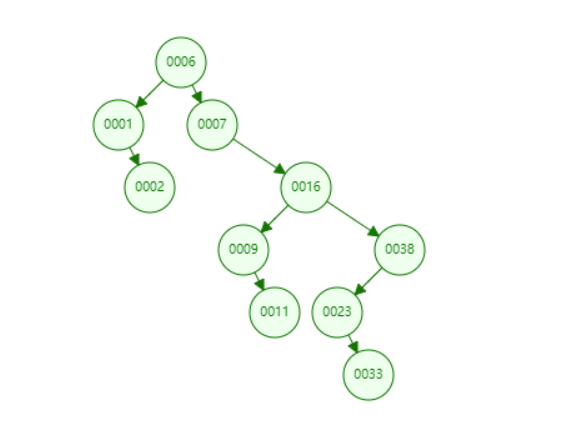
索引樹中存儲的是 key-value 結(jié)構(gòu)的數(shù)據(jù),key 就是索引的值,即 11,而 value 則是 id = 11 這一行數(shù)據(jù)在磁盤中的地址,所以查找的順序是先找到索引對應(yīng)的 key 值,從而獲取到 value 值,也就是數(shù)據(jù)行的地址,進(jìn)而就可以直接獲取到數(shù)據(jù)行了,只需要讀取一次磁盤即可,速度就快了很多倍,大大提升了效率。
但是楠哥要告訴大家,MySQL 索引底層其實用的并不是二叉樹,因為二叉樹還不夠優(yōu)化,面對海量數(shù)據(jù)的時候,它的效率還是遠(yuǎn)遠(yuǎn)不夠的,關(guān)于二叉樹的性能劣勢,通過下面這個例子你就清清楚楚了,比如,現(xiàn)在的數(shù)據(jù)如下所示。
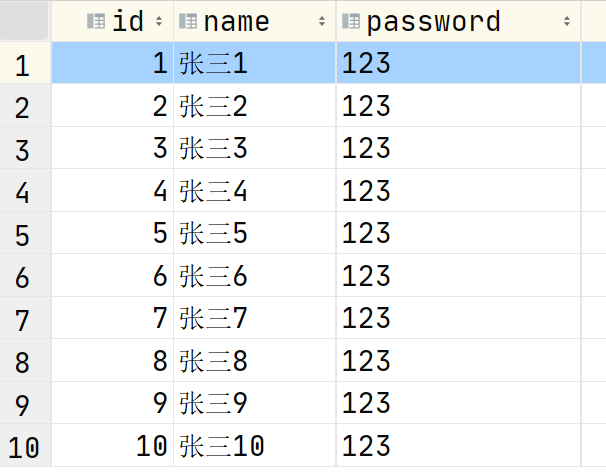
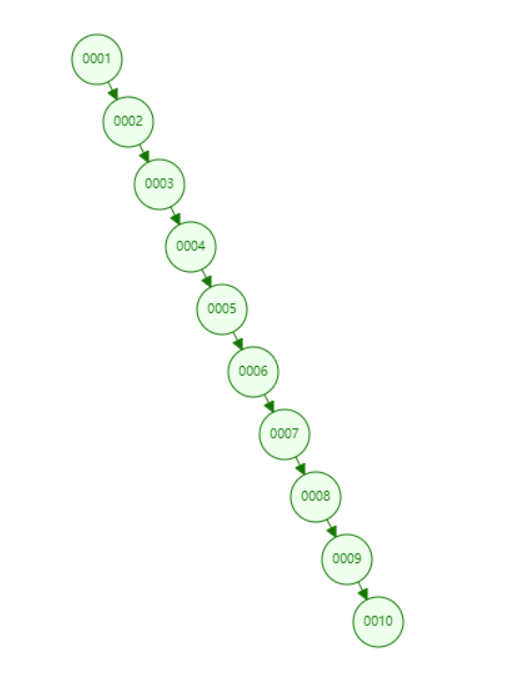
想必大家已經(jīng)發(fā)現(xiàn)問題了,這樣的二叉樹其實就是一個鏈表,則查找 id = 10 的數(shù)據(jù),依然要查找 10 次,效率非常低,和不建索引直接逐行查找沒有什么區(qū)別,所以單純使用二叉樹,肯定是不合適的。
那么應(yīng)該采用什么數(shù)據(jù)結(jié)構(gòu)呢?有的同學(xué)可能會說了紅黑樹,確實,紅黑樹本身就是一個平衡二叉樹,可以避免二叉樹退化成鏈表的情況,我們現(xiàn)在用紅黑樹來生成上述的索引,如下圖所示。
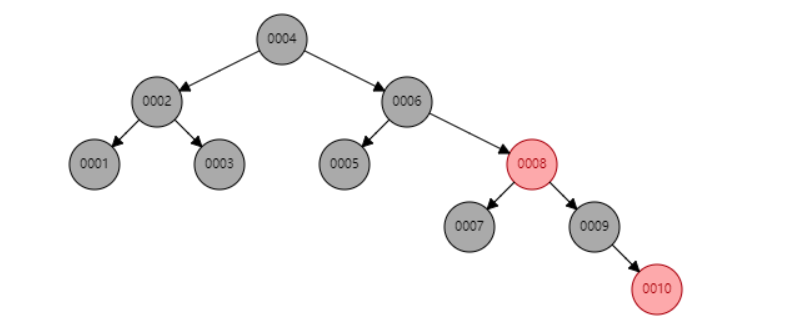
再次查找 id = 10 的數(shù)據(jù),只需要查找 5 次即可找到,效率確實得到了提升。但是請大家思考一下,紅黑樹就是最完美的解決方案嗎?它有沒有什么弊端呢?
很顯然,當(dāng)數(shù)據(jù)量很大的時候,比如千萬級別,此時的紅黑樹雖然可以保持平衡,但是樹的高度會非常大,查詢數(shù)據(jù)同樣需要遍歷很多層,在海量數(shù)據(jù)的情況下,速度依然難以到達(dá)我們的要求,所以,紅黑樹也被 pass 了,那么我們應(yīng)該使用什么數(shù)據(jù)結(jié)構(gòu)呢?這種比紅黑樹效率更高的數(shù)據(jù)結(jié)構(gòu)是什么呢?
我們先分析一下,現(xiàn)在紅黑樹的弊端是樹的高度太大了,那么我們?nèi)绻軐t黑樹進(jìn)行改造,限制樹的高度,不就可以解決問題了嗎?有了思路,接下來楠哥帶你來看如何實現(xiàn)。
我們現(xiàn)在需要存儲大量的數(shù)據(jù),同時還要限制樹的高度,那么解決方法只有一個,就是橫向擴(kuò)展,在同一層上存儲多個節(jié)點,如下圖所示。
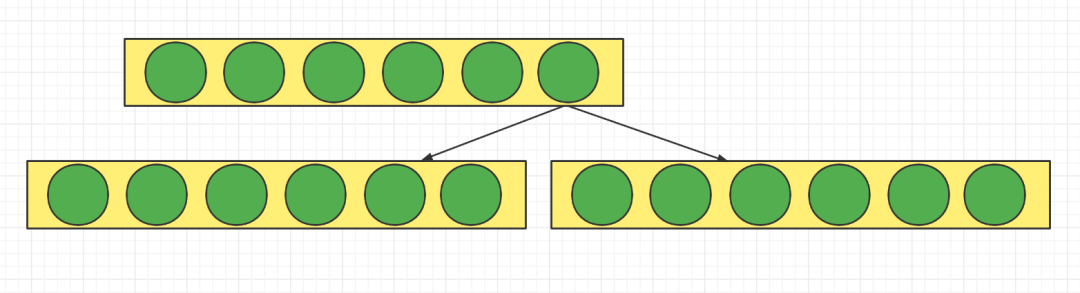
這樣就可以限制樹高度的同時,存儲大量數(shù)據(jù),這種結(jié)構(gòu)就是 B 樹,如下圖所示。
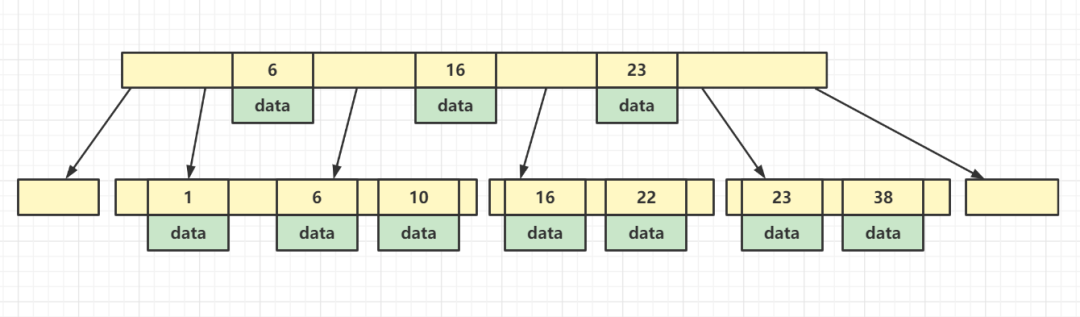
比如現(xiàn)在要查詢 id = 7 的數(shù)據(jù),先在樹的第一層查找,發(fā)現(xiàn)沒有 id = 7 的索引,但是發(fā)現(xiàn)它在 6-16 之間,則通過 6-16 之間存儲的地址找到第二層大于 6 的區(qū)域,然后從在這個區(qū)域中很快可以找到 id = 7 的數(shù)據(jù),這種方式類似于折半查找法。
到這還沒完,MySQL 索引所采用的數(shù)據(jù)結(jié)構(gòu)并不是 B 樹,而是對B 樹又進(jìn)行了一次優(yōu)化,把 data 值全部存儲到葉子節(jié)點,即非葉子節(jié)點不存儲 data,只存儲索引的值,如下所示。
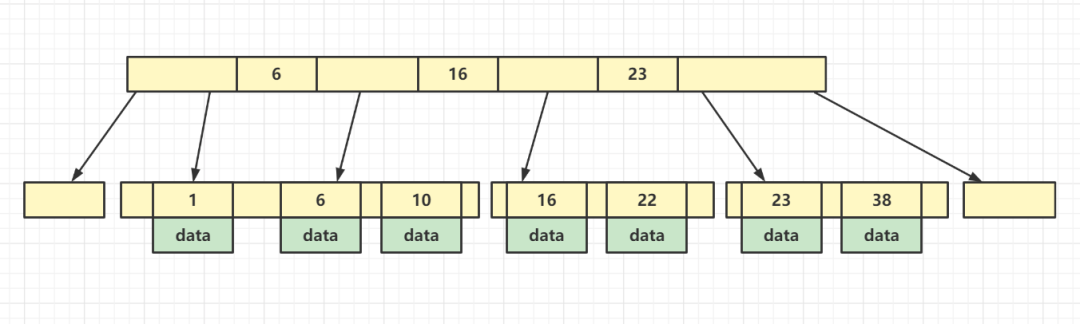
這樣修改的好處是什么呢?我們知道樹的每一層存儲空間都是有限的,大概是 16 KB,那么如果在這存儲 data,每一個元素所占用的空間就更大,所存儲的元素個數(shù)就越少。
如果把 data 去掉,就意味著每一層可以存儲更多的索引,從而降低樹的高度,從另外一個角度來說,非葉子節(jié)點存儲的都是冗余索引,即在它的下一層同樣會記錄這個索引值,也就是說非葉子節(jié)點存儲的索引都是一些中間值,是用來分割的,把所有的數(shù)據(jù)按大小分割成一段一段的形式,再進(jìn)行折半查找。
所以,真正的 B+ 樹就是非葉子節(jié)點只存儲索引值,葉子節(jié)點存儲完整的索引值 + data,而這個 data 就是 MySQL 數(shù)據(jù)庫中對應(yīng)數(shù)據(jù)行的地址,通過 B+ 樹的結(jié)構(gòu)快速找到索引,進(jìn)而獲取 data,再讀取到磁盤中的數(shù)據(jù),這就是 MySQL 索引的底層數(shù)據(jù)結(jié)構(gòu),以及查找數(shù)據(jù)的原理。
這樣的結(jié)構(gòu)真的可以支持海量數(shù)據(jù)的快速檢索嗎?我們來推算一下,MySQL 分配給每一級的空間大小是 16 KB,非葉子節(jié)點的單位大小是 14 byte,那么可以計算出一層非葉子節(jié)點可以存儲的索引個數(shù)大概是1170 個。葉子節(jié)點因為會存儲 data,所占空間會大一些,大概是 1 KB,則一層葉子節(jié)點可以存儲元素個數(shù)為 16。
那么如果是一棵樹高為 3 的 B+ 樹,兩層非葉子節(jié)點,一層葉子節(jié)點,一共可以存儲的索引個數(shù)為 1170*1170*16 = 2190W,你可以看到,僅需要一個 3 層高度的 B+ 樹,就可以存儲千萬級別的數(shù)據(jù)量,同時查找速度也是非常快的。
以上就是關(guān)于 MySQL 索引數(shù)據(jù)結(jié)構(gòu)的分享,你學(xué)會了嗎?
楠哥簡介
資深 Java 工程師,微信號 southwindss
《Java零基礎(chǔ)實戰(zhàn)》一書作者
騰訊課程官方 Java 面試官,今日頭條認(rèn)證大V
GitChat認(rèn)證作者,B站認(rèn)證UP主(楠哥教你學(xué)Java)
致力于幫助萬千 Java 學(xué)習(xí)者持續(xù)成長。

