迭代(iteration)和遞歸(recursion)
一、
Q.請(qǐng)寫(xiě)一段代碼來(lái)計(jì)算給定文本(AAA rating)內(nèi)字符“A”的個(gè)數(shù)。分別用迭代和遞歸兩種方式。
A.
迭代方式的代碼如下:
public class Iteration {
?
????public int countA(String input) {
????????if (input == null || input.length( ) == 0) {
????????????return 0;
????????}
?
????????int count = 0;
????????for (int i = 0; i < input.length( ); i++) {
????????????if(input.substring(i, i+1).equals("A")){
????????????????count++;
????????????}
????????}
????????return count;
????}
?
????public static void main(String[ ] args) {
??????????System.out.println(new Iteration( ).countA("AAA rating"));???? // Ans.3
????}
}
遞歸方式的代碼如下:
public class RecursiveCall {
?
????public int countA(String input) {
?
????????// exit condition – recursive calls must have an exit condition
????????if (input == null || input.length( ) == 0) {
????????????return 0;
????????}
?
????????int count = 0;
?
????????//check first character of the input
????????if (input.substring(0, 1).equals("A")) {
????????????count = 1;
????????}
?
????????//recursive call to evaluate rest of the input
????????//(i.e.? 2nd character onwards)
????????return count + countA(input.substring(1));
????}
?
????public static void main(String[ ] args) {
????????System.out.println(new RecursiveCall( ).countA("AAA rating"));? // Ans. 3
????}
}
Q.什么情況下應(yīng)該采用遞歸?
A. 上面的例子中其實(shí)不必采用遞歸,循環(huán)的方式可以達(dá)到目的,但是在某些情況下采用遞歸方式則代碼會(huì)更加簡(jiǎn)短易讀。遞歸方法在循環(huán)樹(shù)結(jié)構(gòu)以及避免丑陋的嵌套循環(huán)的情況下是非常好用的。
Q.尾遞歸的好處是什么?上面的代碼用尾遞歸方式如何重寫(xiě)?
A.
????常規(guī)遞歸方法(亦稱,頭遞歸)在上面演示了,這種方式會(huì)增加調(diào)用棧的大小。每次遞歸,其入口需要被記錄在棧中。方法返回之前需要給countA(input.substring(1)的結(jié)果加一個(gè)count。假定count大于1,那么返回結(jié)果就是count + countA(input.substring(1)),當(dāng)然事先要算出來(lái)countA(input.substring(1))才行。同時(shí),這也意味著直到countA(input.substring(1)計(jì)算出來(lái)才能得到最終的結(jié)果。因此,最后需要做的事其實(shí)是加法運(yùn)算,而非遞歸本身。
????在尾遞歸中,最后要做的是遞歸,加法運(yùn)算在之前就已經(jīng)完成了。一輪遞歸調(diào)用完畢后就沒(méi)有其他事情了(除了加法運(yùn)算),因此調(diào)用時(shí)生成的信息也就沒(méi)什么用了。這些無(wú)用信息可以丟棄,然后用一組新的參數(shù)來(lái)調(diào)用一次遞歸方法來(lái)產(chǎn)生一個(gè)新的結(jié)果。這也就是說(shuō),棧調(diào)用減少帶來(lái)了內(nèi)存消耗減少并且程序的性能更好。
尾遞歸代碼重寫(xiě)如下:
public class TailRecursiveCall {
?
?public int countA(String input) {
?
??// exit condition – recursive calls must have an exit condition
??if (input == null || input.length() == 0) {
???return 0;
??}
?
??return countA(input, 0) ;
?}
?
?public int countA(String input, int count) {
??if (input.length() == 0) {
???return count;
??}
?
??// check first character of the input
??if (input.substring(0, 1).equals("A")) {
???count = count + 1;
??}
?
??// recursive call is the last call as the count is cumulative
??return countA(input.substring(1), count);
?}
?
?public static void main(String[] args) {
??System.out.println(new TailRecursiveCall().countA("AAA rating"));
?}
}
二、幾個(gè)經(jīng)典遞歸案例
Q.斐波那契數(shù)列
A.斐波那契數(shù)列的排列是:0,1,1,2,3,5,8,13,21,34,55,89,144……依次類推下去,你會(huì)發(fā)現(xiàn),它后一個(gè)數(shù)等于前面兩個(gè)數(shù)的和。在這個(gè)數(shù)列中的數(shù)字,就被稱為斐波那契數(shù)。
遞歸思想:一個(gè)數(shù)等于前兩個(gè)數(shù)的和。
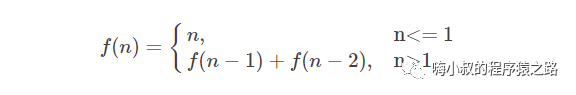
/**
* 斐波那契數(shù)列的遞歸寫(xiě)法 核心:一個(gè)小的解決終點(diǎn),然后大的問(wèn)題可以循環(huán)在小問(wèn)題上解決
*?
* @param n
* @return
*/
private static long F(int n) {
if (n <= 1)
return n;
return F(n - 1) + F(n - 2);
}
/**
* 斐波那契數(shù)列的遞推寫(xiě)法
*?
* @param n
* @return
*/
private static long F1(int n) {
if (n <= 1)
return n;
long fn = 0;
long fn_1 = 1;
long fn_2 = 0;
for (int i = 2; i <= n; i++) {
fn = fn_1 + fn_2;
fn_2 = fn_1;
fn_1 = fn;
}
return fn;
}
public static void main(String[ ] args) {
????System.out.println(F(10)); // Ans. 55
????????????System.out.println(F1(10));?// Ans. 55
}
????可以看到,遞歸寫(xiě)法簡(jiǎn)單優(yōu)美,省去考慮很多邊界條件的時(shí)間。當(dāng)然,遞歸算法會(huì)保存很多的臨時(shí)數(shù)據(jù),類似于堆棧的過(guò)程,如果棧深太深,就會(huì)造成內(nèi)存用盡,程序崩潰的現(xiàn)象。Java為每個(gè)線程分配了棧大小,如果棧大小溢出,就會(huì)報(bào)錯(cuò),這時(shí)候還是選擇遞推好一點(diǎn)。
Q. 階乘(例如5的階乘:5*4*3*2*1=120)
A.遞歸思想:n! = n * (n-1)!
代碼如下:
private static long factorial(int n){
? ? if (n <=1) return 1;
? ? return factorial(n-1)*n;
}
Q.倒序輸出一個(gè)正整數(shù)(例如n=12345,希望逆序輸出54321)
A.
遞歸思想:首先輸出這個(gè)數(shù)的個(gè)位數(shù),然后再輸出前面數(shù)字的個(gè)位數(shù),直到之前沒(méi)數(shù)字。
/**
* 倒序輸出正整數(shù)的各位數(shù)
* @param n
*/
private static void printDigit(int n){
? ? System.out.print(n%10);
? ? if (n > 10){
? ? ? ? printDigit(n/10);
? ? }
}
Q.漢諾塔
A.數(shù)學(xué)描述就是:
有三根桿子X(jué),Y,Z。X桿上有N個(gè)(N>1)穿孔圓盤(pán),盤(pán)的尺寸由下到上依次變小。要求按下列規(guī)則將所有圓盤(pán)移至Y桿:?
1. 每次只能移動(dòng)一個(gè)圓盤(pán);?
2. 大盤(pán)不能疊在小盤(pán)上面。
遞歸思想:?
1. 將X桿上的n-1個(gè)圓盤(pán)都移到空閑的Z桿上,并且滿足上面的所有條件?
2. 將X桿上的第n個(gè)圓盤(pán)移到Y(jié)上?
3. 剩下問(wèn)題就是將Z桿上的n-1個(gè)圓盤(pán)移動(dòng)到Y(jié)上了
公式描述有點(diǎn)麻煩,用語(yǔ)言描述下吧:?
1. 以Y桿為中介,將前n-1個(gè)圓盤(pán)從X桿挪到Z桿上(本身就是一個(gè)n-1的漢諾塔問(wèn)
題了!)?
2. 將第n個(gè)圓盤(pán)移動(dòng)到Y(jié)桿上?
3. 以X桿為中介,將Z桿上的n-1個(gè)圓盤(pán)移到Y(jié)桿上(本身就是一個(gè)n-1的漢諾塔問(wèn)題了!)
代碼如下:
