人人做人人爱免费的视频,无码高清免费视频,亚洲黄色精品视频,日本成人1024,神马午夜国产精品,福利视频一区,特级日本欧美日韩亚洲精品综合免费在线 ,久久精品在

↑↑↑關(guān)注后"星標(biāo)"Datawhale

Datawhale干貨

作者：DengBoCong，編輯：極市平臺

來源：https://zhuanlan.zhihu.com/p/343564175

論文標(biāo)題：An overview of gradient descent optimization algorithms
原文鏈接：https://arxiv.org/pdf/1609.04747.pdf
Github：NLP相關(guān)Paper筆記和代碼復(fù)現(xiàn)（https://github.com/DengBoCong/nlp-paper）
說明：閱讀論文時進(jìn)行相關(guān)思想、結(jié)構(gòu)、優(yōu)缺點(diǎn)，內(nèi)容進(jìn)行提煉和記錄，論文和相關(guān)引用會標(biāo)明出處，引用之處如有侵權(quán)，煩請告知刪除。

不管是使用PyTorch還是TensorFlow，用多了Optimizer優(yōu)化器封裝好的函數(shù)，對其內(nèi)部使用的優(yōu)化算法卻沒有仔細(xì)研究過，也很難對其優(yōu)點(diǎn)和缺點(diǎn)進(jìn)行實用的解釋。所以打算以這一篇論文為主線并結(jié)合多篇優(yōu)秀博文，回顧和總結(jié)目前主流的優(yōu)化算法，對于沒有深入了解過的算法，正好借這個機(jī)會學(xué)習(xí)一下。

寫在前面

當(dāng)前使用的許多優(yōu)化算法，是對梯度下降法的衍生和優(yōu)化。在微積分中，對多元函數(shù)的參數(shù)求偏導(dǎo)數(shù)，把求得的各個參數(shù)的導(dǎo)數(shù)以向量的形式寫出來就是梯度。梯度就是函數(shù)變化最快的地方。梯度下降是迭代法的一種，在求解機(jī)器學(xué)習(xí)算法的模型參數(shù) 時，即無約束問題時，梯度下降是最常采用的方法之一。

這里定義一個通用的思路框架，方便我們后面理解各算法之間的關(guān)系和改進(jìn)。首先定義待優(yōu)化參數(shù) ，目標(biāo)函數(shù) ，學(xué)習(xí)率為，然后我們進(jìn)行迭代優(yōu)化，假設(shè)當(dāng)前的epoch為，則有：

計算目標(biāo)函數(shù)關(guān)于當(dāng)前參數(shù)的梯度：
根據(jù)歷史梯度計算一階動量和二階動量：，
計算當(dāng)前時刻的下降梯度：
根據(jù)下降梯度進(jìn)行更新：

其中，為下一個時刻的參數(shù)，為當(dāng)前時刻參數(shù)，后面的描述我們都將結(jié)合這個框架來進(jìn)行。

這里提一下一些概念：

鞍點(diǎn)：一個光滑函數(shù)的鞍點(diǎn)鄰域的曲線，曲面，或超曲面，都位于這點(diǎn)的切線的不同邊。例如這個二維圖形，像個馬鞍：在x-軸方向往上曲，在y-軸方向往下曲，鞍點(diǎn)就是（0，0）。

指數(shù)加權(quán)平均、偏差修正：可參見這篇文章

什么是指數(shù)加權(quán)平均、偏差修正？- 郭耀華 - 博客園

https://www.cnblogs.com/guoyaohua/p/8544835.html

Gradient Descent（GD）

在GD中沒有動量的概念，也就是說在上述框架中：，則我們在當(dāng)前時刻需要下降的梯度就是，則使用梯度下降法更新參數(shù)為（假設(shè)當(dāng)前樣本為，每當(dāng)樣本輸入時，參數(shù)即進(jìn)行更新）：

梯度下降算法中，模型參數(shù)的更新調(diào)整，與代價函數(shù)關(guān)于模型參數(shù)的梯度有關(guān)，即沿著梯度的方向不斷減小模型參數(shù)，從而最小化代價函數(shù)。基本策略可以理解為”在有限視距內(nèi)尋找最快路徑下山“，因此每走一步，參考當(dāng)前位置最陡的方向(即梯度)進(jìn)而邁出下一步，更形象的如下圖：

標(biāo)準(zhǔn)的梯度下降主要有兩個缺點(diǎn)：

訓(xùn)練速度慢：在應(yīng)用于大型數(shù)據(jù)集中，每輸入一個樣本都要更新一次參數(shù)，且每次迭代都要遍歷所有的樣本，會使得訓(xùn)練過程及其緩慢，需要花費(fèi)很長時間才能得到收斂解。
容易陷入局部最優(yōu)解：由于是在有限視距內(nèi)尋找下山的反向，當(dāng)陷入平坦的洼地，會誤以為到達(dá)了山地的最低點(diǎn)，從而不會繼續(xù)往下走。所謂的局部最優(yōu)解就是鞍點(diǎn)，落入鞍點(diǎn)，梯度為0，使得模型參數(shù)不在繼續(xù)更新。

Batch Gradient Descent（BGD）

BGD相對于標(biāo)準(zhǔn)GD進(jìn)行了改進(jìn)，改進(jìn)的地方通過它的名字應(yīng)該也能看出來，也就是不再是想標(biāo)準(zhǔn)GD一樣，對每個樣本輸入都進(jìn)行參數(shù)更新，而是針對一個批量的數(shù)據(jù)輸入進(jìn)行參數(shù)更新。我們假設(shè)批量訓(xùn)練樣本總數(shù)為，樣本為，則在第對樣本上損失函數(shù)關(guān)于參數(shù)的梯度為 , 則使用BGD更新參數(shù)為：

從上面的公式我們可以看到，BGD其實是在一個批量的樣本數(shù)據(jù)中，求取該批量樣本梯度的均值來更新參數(shù)，即每次權(quán)值調(diào)整發(fā)生在批量樣本輸入之后，而不是每輸入一個樣本就更新一次模型參數(shù)，這樣就會大大加快訓(xùn)練速度，但是還是不夠，我們接著往下看。

Stochastic Gradient Descent（SGD）

隨機(jī)梯度下降法，不像BGD每一次參數(shù)更新，需要計算整個數(shù)據(jù)樣本集的梯度，而是每次參數(shù)更新時，僅僅選取一個樣本計算其梯度，參數(shù)更新公式為：

公式看起來和上面標(biāo)準(zhǔn)GD一樣，但是注意了，這里的樣本是從批量中隨機(jī)選取一個，而標(biāo)準(zhǔn)GD是所有的輸入樣本都進(jìn)行計算。可以看到BGD和SGD是兩個極端，SGD由于每次參數(shù)更新僅僅需要計算一個樣本的梯度，訓(xùn)練速度很快，即使在樣本量很大的情況下，可能只需要其中一部分樣本就能迭代到最優(yōu)解，由于每次迭代并不是都向著整體最優(yōu)化方向，導(dǎo)致梯度下降的波動非常大（如下圖），更容易從一個局部最優(yōu)跳到另一個局部最優(yōu)，準(zhǔn)確度下降。

論文中提到，當(dāng)緩慢降低學(xué)習(xí)率時，SGD會顯示與BGD相同的收斂行為，幾乎一定會收斂到局部（非凸優(yōu)化）或全局最小值（凸優(yōu)化）。

SGD的優(yōu)點(diǎn)：

雖然看起來SGD波動非常大，會走很多彎路，但是對梯度的要求很低（計算梯度快），而且對于引入噪聲，大量的理論和實踐工作證明，只要噪聲不是特別大，SGD都能很好地收斂。
應(yīng)用大型數(shù)據(jù)集時，訓(xùn)練速度很快。比如每次從百萬數(shù)據(jù)樣本中，取幾百個數(shù)據(jù)點(diǎn)，算一個SGD梯度，更新一下模型參數(shù)。相比于標(biāo)準(zhǔn)梯度下降法的遍歷全部樣本，每輸入一個樣本更新一次參數(shù)，要快得多。

SGD的缺點(diǎn)：

SGD在隨機(jī)選擇梯度的同時會引入噪聲，使得權(quán)值更新的方向不一定正確（次要）。
SGD也沒能單獨(dú)克服局部最優(yōu)解的問題（主要）。

Mini-batch Gradient Descent（MBGD，也叫作SGD）

小批量梯度下降法就是結(jié)合BGD和SGD的折中，對于含有個訓(xùn)練樣本的數(shù)據(jù)集，每次參數(shù)更新，選擇一個大小為 $m(m<n)$ 的mini-batch數(shù)據(jù)樣本計算其梯度，其參數(shù)更新公式如下：< p>

小批量梯度下降法即保證了訓(xùn)練的速度，又能保證最后收斂的準(zhǔn)確率，目前的SGD默認(rèn)是小批量梯度下降算法。常用的小批量尺寸范圍在50到256之間，但可能因不同的應(yīng)用而異。

MBGD的缺點(diǎn)：

Mini-batch gradient descent 不能保證很好的收斂性，learning rate 如果選擇的太小，收斂速度會很慢，如果太大，loss function 就會在極小值處不停地震蕩甚至偏離（有一種措施是先設(shè)定大一點(diǎn)的學(xué)習(xí)率，當(dāng)兩次迭代之間的變化低于某個閾值后，就減小 learning rate，不過這個閾值的設(shè)定需要提前寫好，這樣的話就不能夠適應(yīng)數(shù)據(jù)集的特點(diǎn)）。對于非凸函數(shù)，還要避免陷于局部極小值處，或者鞍點(diǎn)處，因為鞍點(diǎn)所有維度的梯度都接近于0，SGD 很容易被困在這里（會在鞍點(diǎn)或者局部最小點(diǎn)震蕩跳動，因為在此點(diǎn)處，如果是BGD的訓(xùn)練集全集帶入，則優(yōu)化會停止不動，如果是mini-batch或者SGD，每次找到的梯度都是不同的，就會發(fā)生震蕩，來回跳動）。
SGD對所有參數(shù)更新時應(yīng)用同樣的 learning rate，如果我們的數(shù)據(jù)是稀疏的，我們更希望對出現(xiàn)頻率低的特征進(jìn)行大一點(diǎn)的更新，且learning rate會隨著更新的次數(shù)逐漸變小。

Momentum

momentum算法思想：參數(shù)更新時在一定程度上保留之前更新的方向，同時又利用當(dāng)前batch的梯度微調(diào)最終的更新方向，簡言之就是通過積累之前的動量來加速當(dāng)前的梯度。從這里開始，我們引入一階動量的概念（在mini-batch SGD的基礎(chǔ)之上），也就是說，在最開始說的框架中，，而不變，參數(shù)更新公式如下：

一階動量是各個時刻梯度方向的指數(shù)移動平均值，約等于最近個時刻的梯度向量和的平均值（移動平均是啥看最上面的文章）。也就是說，時刻的下降方向，不僅由當(dāng)前點(diǎn)的梯度方向決定，而且由此前累積的下降方向決定。的經(jīng)驗值為0.9，這就意味著下降方向主要是此前累積的下降方向，并略微偏向當(dāng)前時刻的下降方向。在梯度方向改變時，momentum能夠降低參數(shù)更新速度，從而減少震蕩，在梯度方向相同時，momentum可以加速參數(shù)更新，從而加速收斂，如下圖：

動量主要解決SGD的兩個問題：

隨機(jī)梯度的方法（引入的噪聲）
Hessian矩陣病態(tài)問題（可以理解為SGD在收斂過程中和正確梯度相比來回擺動比較大的問題）。

Nesterov Accelerated Gradient

NAG(Nesterov accelerated gradient）算法，是Momentum動量算法的變種。momentum保留了上一時刻的梯度，對其沒有進(jìn)行任何改變，NAG是momentum的改進(jìn)，在梯度更新時做一個矯正，具體做法就是在當(dāng)前的梯度上添加上一時刻的動量，梯度改變?yōu)?nbsp; ，參數(shù)更新公式如下：

加上nesterov項后，梯度在大的跳躍后，進(jìn)行計算對當(dāng)前梯度進(jìn)行校正。下圖是momentum和nesterrov的對比表述圖如下：

Nesterov動量梯度的計算在模型參數(shù)施加當(dāng)前速度之后，因此可以理解為往標(biāo)準(zhǔn)動量中添加了一個校正因子。在凸批量梯度的情況下，Nesterov動量將額外誤差收斂率從 (k步后)改進(jìn)到，然而，在隨機(jī)梯度情況下，Nesterov動量對收斂率的作用卻不是很大。

Momentum和Nexterov都是為了使梯度更新更靈活。但是人工設(shè)計的學(xué)習(xí)率總是有些生硬，下面介紹幾種自適應(yīng)學(xué)習(xí)率的方法。

Adagrad

Adagrad其實是對學(xué)習(xí)率進(jìn)行了一個約束，對于經(jīng)常更新的參數(shù)，我們已經(jīng)積累了大量關(guān)于它的知識，不希望被單個樣本影響太大，希望學(xué)習(xí)速率慢一些；對于偶爾更新的參數(shù)，我們了解的信息太少，希望能從每個偶然出現(xiàn)的樣本身上多學(xué)一些，即學(xué)習(xí)速率大一些。而該方法中開始使用二階動量，才意味著“自適應(yīng)學(xué)習(xí)率”優(yōu)化算法時代的到來。

我們前面都沒有好好的討論二階動量，二階動量是個啥？它是用來度量歷史更新頻率的，二階動量是迄今為止所有梯度值的平方和，即，在最上面的框架中（在這里），也就是說，我們的學(xué)習(xí)率現(xiàn)在是（一般為了避免分母為0，會在分母上加一個小的平滑項），從這里我們就會發(fā)現(xiàn) 是恒大于0的，而且參數(shù)更新越頻繁，二階動量越大，學(xué)習(xí)率就越小，這一方法在稀疏數(shù)據(jù)場景下表現(xiàn)非常好，參數(shù)更新公式如下：

細(xì)心的小伙伴應(yīng)該會發(fā)現(xiàn)Adagrad還是存在一個很明顯的缺點(diǎn)：

仍需要手工設(shè)置一個全局學(xué)習(xí)率 , 如果設(shè)置過大的話，會使regularizer過于敏感，對梯度的調(diào)節(jié)太大
中后期，分母上梯度累加的平方和會越來越大，使得參數(shù)更新量趨近于0，使得訓(xùn)練提前結(jié)束，無法學(xué)習(xí)

Adadelta

由于AdaGrad調(diào)整學(xué)習(xí)率變化過于激進(jìn)，我們考慮一個改變二階動量計算方法的策略：不累積全部歷史梯度，而只關(guān)注過去一段時間窗口的下降梯度，即Adadelta只累加固定大小的項，并且也不直接存儲這些項，僅僅是近似計算對應(yīng)的平均值（指數(shù)移動平均值），這就避免了二階動量持續(xù)累積、導(dǎo)致訓(xùn)練過程提前結(jié)束的問題了，參數(shù)更新公式如下：

觀察上面的參數(shù)更新公式，我們發(fā)現(xiàn)還是依賴于全局學(xué)習(xí)率，但是原作者在此基礎(chǔ)之上做出了一定的處理，上式經(jīng)過牛頓迭代法之后，得到Adadelta最終迭代公式如下式，其中：

此時可以看出Adadelta已經(jīng)不依賴全局learning rate了，Adadelta有如下特點(diǎn)：

訓(xùn)練初中期，加速效果不錯，很快
訓(xùn)練后期，反復(fù)在局部最小值附近抖動

RMSprop

RMSProp算法修改了AdaGrad的梯度平方和累加為指數(shù)加權(quán)的移動平均，使得其在非凸設(shè)定下效果更好。設(shè)定參數(shù)：全局初始率 , 默認(rèn)設(shè)為0.001，decay rate ，默認(rèn)設(shè)置為0.9，一個極小的常量，通常為10e-6，參數(shù)更新公式如下，其中：

其實RMSprop依然依賴于全局學(xué)習(xí)率
RMSprop算是Adagrad的一種發(fā)展，和Adadelta的變體，效果趨于二者之間
適合處理非平穩(wěn)目標(biāo)(包括季節(jié)性和周期性)——對于RNN效果很好

Adaptive Moment Estimation（Adam）

其實有了前面的方法，Adam和Nadam的出現(xiàn)就很理所當(dāng)然的了，因為它們結(jié)合了前面方法的一階動量和二階動量。我們看到，SGD-M和NAG在SGD基礎(chǔ)上增加了一階動量，AdaGrad和AdaDelta在SGD基礎(chǔ)上增加了二階動量，參數(shù)更新公式如下（按照最開始總結(jié)的計算框架）：

通常情況下，默認(rèn)值為、和，Adam通常被認(rèn)為對超參數(shù)的選擇相當(dāng)魯棒，特點(diǎn)如下：

Adam梯度經(jīng)過偏置校正后，每一次迭代學(xué)習(xí)率都有一個固定范圍，使得參數(shù)比較平穩(wěn)。
結(jié)合了Adagrad善于處理稀疏梯度和RMSprop善于處理非平穩(wěn)目標(biāo)的優(yōu)點(diǎn)
為不同的參數(shù)計算不同的自適應(yīng)學(xué)習(xí)率
也適用于大多非凸優(yōu)化問題——適用于大數(shù)據(jù)集和高維空間。

AdaMax

Adamax是Adam的一種變體，此方法對學(xué)習(xí)率的上限提供了一個更簡單的范圍，即使用無窮范式，參數(shù)更新公式如下：

通常情況下，默認(rèn)值為、和

Nadam

其實如果說要集成所有方法的優(yōu)點(diǎn)于一身的話，Nadam應(yīng)該就是了，Adam遺漏了啥？沒錯，就是Nesterov項，我們在Adam的基礎(chǔ)上，加上Nesterov項就是Nadam了，參數(shù)更新公式如下：

可以看出，Nadam對學(xué)習(xí)率有更強(qiáng)的約束，同時對梯度的更新也有更直接的影響。一般而言，在使用帶動量的RMSprop或Adam的問題上，使用Nadam可以取得更好的結(jié)果。

來張直觀的動態(tài)圖展示上述優(yōu)化算法的效果：

下圖描述了在一個曲面上，6種優(yōu)化器的表現(xiàn)：

下圖在一個存在鞍點(diǎn)的曲面，比較6中優(yōu)化器的性能表現(xiàn)：

下圖圖比較了6種優(yōu)化器收斂到目標(biāo)點(diǎn)（五角星）的運(yùn)行過程

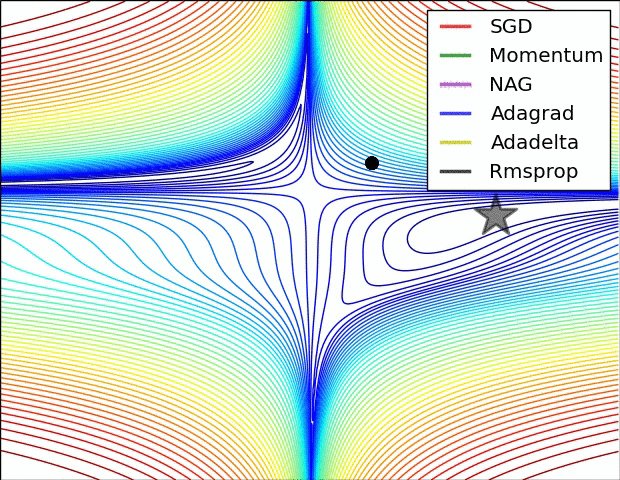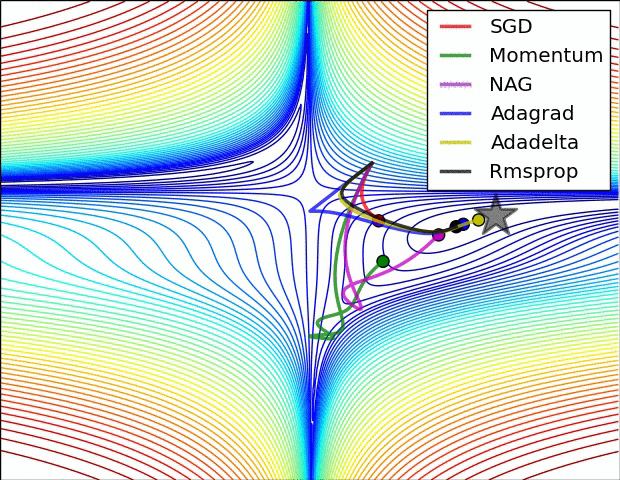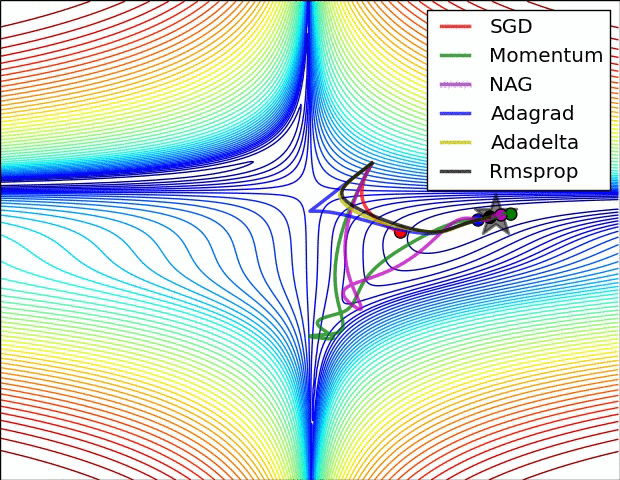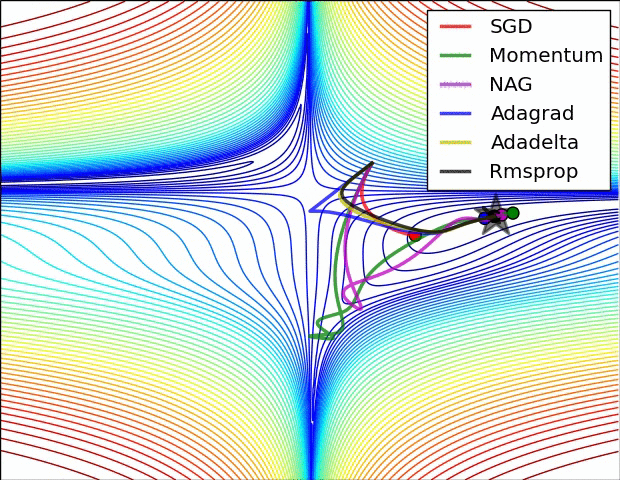
總結(jié)

那種優(yōu)化器最好？該選擇哪種優(yōu)化算法？目前還沒能夠達(dá)達(dá)成共識。Schaul et al (2014)展示了許多優(yōu)化算法在大量學(xué)習(xí)任務(wù)上極具價值的比較。雖然結(jié)果表明，具有自適應(yīng)學(xué)習(xí)率的優(yōu)化器表現(xiàn)的很魯棒，不分伯仲，但是沒有哪種算法能夠脫穎而出。

目前，最流行并且使用很高的優(yōu)化器（算法）包括SGD、具有動量的SGD、RMSprop、具有動量的RMSProp、AdaDelta和Adam。在實際應(yīng)用中，選擇哪種優(yōu)化器應(yīng)結(jié)合具體問題；同時，也優(yōu)化器的選擇也取決于使用者對優(yōu)化器的熟悉程度（比如參數(shù)的調(diào)節(jié)等等）。

對于稀疏數(shù)據(jù)，盡量使用學(xué)習(xí)率可自適應(yīng)的優(yōu)化方法，不用手動調(diào)節(jié)，而且最好采用默認(rèn)值
SGD通常訓(xùn)練時間更長，但是在好的初始化和學(xué)習(xí)率調(diào)度方案的情況下，結(jié)果更可靠
如果在意更快的收斂，并且需要訓(xùn)練較深較復(fù)雜的網(wǎng)絡(luò)時，推薦使用學(xué)習(xí)率自適應(yīng)的優(yōu)化方法。
Adadelta，RMSprop，Adam是比較相近的算法，在相似的情況下表現(xiàn)差不多。
在想使用帶動量的RMSprop，或者Adam的地方，大多可以使用Nadam取得更好的效果
如果驗證損失較長時間沒有得到改善，可以停止訓(xùn)練。
添加梯度噪聲（高斯分布）到參數(shù)更新，可使網(wǎng)絡(luò)對不良初始化更加健壯，并有助于訓(xùn)練特別深而復(fù)雜的網(wǎng)絡(luò)。

參考文獻(xiàn)：

An overview of gradient descent optimization algorithms（https://ruder.io/optimizing-gradient-descent/）
深度學(xué)習(xí)最全優(yōu)化方法總結(jié)比較（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）（https://zhuanlan.zhihu.com/p/22252270）
visualize_optimizers（https://github.com/snnclsr/visualize_optimizers）
lossfunctions（https://lossfunctions.tumblr.com/）
優(yōu)化算法Optimizer比較和總結(jié)（https://zhuanlan.zhihu.com/p/55150256）
一個框架看懂優(yōu)化算法之異同 SGD/AdaGrad/Adam（https://zhuanlan.zhihu.com/p/32230623）
深度學(xué)習(xí)——優(yōu)化器算法Optimizer詳解（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam）（https://www.cnblogs.com/guoyaohua/p/8542554.html）
機(jī)器學(xué)習(xí)：各種優(yōu)化器Optimizer的總結(jié)與比較（https://blog.csdn.net/weixin_40170902/article/details/80092628）
optimizer優(yōu)化算法總結(jié)（https://blog.csdn.net/muyu709287760/article/details/62531509#%E4%B8%89%E7%A7%8Dgradient-descent%E5%AF%B9%E6%AF%94）

“整理不易，點(diǎn)贊三連↓

各種 Optimizer 梯度下降優(yōu)化算法總結(jié)