?LeetCode刷題實(shí)戰(zhàn)77：組合
算法的重要性，我就不多說了吧，想去大廠，就必須要經(jīng)過基礎(chǔ)知識(shí)和業(yè)務(wù)邏輯面試+算法面試。所以，為了提高大家的算法能力，這個(gè)公眾號(hào)后續(xù)每天帶大家做一道算法題，題目就從LeetCode上面選 ！
今天和大家聊的問題叫做?組合，我們先來看題面：
https://leetcode-cn.com/problems/combinations/
Given two integers n and k, return all possible combinations of k numbers out of 1 ... n.
You may return the answer in any order.
題意
輸入: n = 4, k = 2
輸出:
[
??[2,4],
??[3,4],
??[2,3],
??[1,2],
??[1,3],
??[1,4],
]
解題
遞歸
class?Solution:
????def?combine(self, n: int, k: int)?-> List[List[int]]:
????????def?dfs(start, cur):
????????????# 如果當(dāng)前已經(jīng)拿到了K個(gè)數(shù)的組合，直接加入答案
????????????# 注意要做深拷貝，否則在之后的回溯過程當(dāng)中變動(dòng)也會(huì)影響結(jié)果
????????????if?len(cur) == k:
????????????????ret.append(cur[:])
????????????????return
????????????
????????????# 從start+1的位置開始遍歷
????????????for?i in?range(start+1, n):
????????????????cur.append(i+1)
????????????????dfs(i, cur)
????????????????# 回溯
????????????????cur.pop()
????????????????
????????ret = []
????????dfs(-1, [])
????????return?ret
迭代
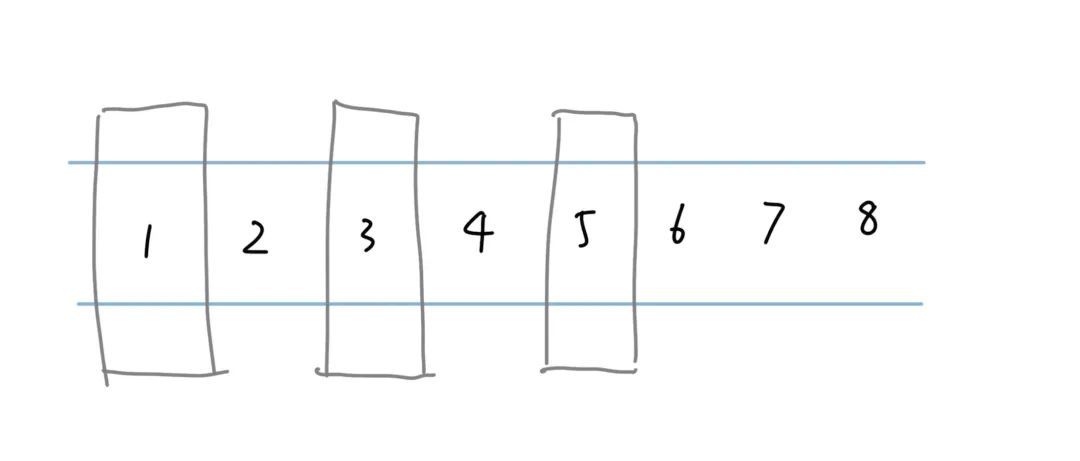
的組合都已經(jīng)獲取完了。如果n+1的位置還有滑動(dòng)框，并且它的右側(cè)還可以移動(dòng)，那么我們需要將它往右移動(dòng)一個(gè)，到n+2的位置。這個(gè)時(shí)候剩下的局面就是
，為了獲取這些組合，我們需要把這m個(gè)滑動(dòng)框全部再移動(dòng)到直尺的最左側(cè)，重新開始移動(dòng)。class Solution:
????def combine(self, n: int, k: int) -> List[List[int]]:
????????def comb(window, m, ret):
????????????ret.append(window[:-1])
????????????# 如果第m位的滑動(dòng)框不超過直尺的范圍并且m右側(cè)的滑動(dòng)框
????????????while?window[m] < min(n - k?+ m?+ 1, window[m+1] - 1):
????????????????# 向右滑動(dòng)一位
????????????????window[m] += 1
????????????????# 如果m左側(cè)還有滑動(dòng)框，遞歸
????????????????if?m?> 0:
????????????????????# 把左側(cè)的滑動(dòng)框全部移動(dòng)到最左側(cè)
????????????????????window[:m] = range(1, m+1)
????????????????????comb(window, m-1, ret)
????????????????else:
????????????????????# 否則記錄答案
????????????????????ret.append(window[:-1])
????????????????
????????ret?= []
????????window = list(range(1, k+1))
????????# 額外多放一個(gè)滑動(dòng)框作為標(biāo)兵
????????window.append(n+1)
????????comb(window, k-1, ret)
????????return?ret
class?Solution:
????def?combine(self, n:?int, k:?int)?-> List[List[int]]:
????????# 構(gòu)造滑動(dòng)框
????????window = list(range(1, k + 1)) + [n + 1]
????????
????????ret, j = [], 0
????????while?j < k:
????????????# 添加答案
????????????ret.append(window[:k])
????????????j = 0
????????????# 從最左側(cè)的滑動(dòng)框開始判斷
????????????# 如果滑動(dòng)框與它右側(cè)滑動(dòng)框挨著，那么就將它移動(dòng)到最左側(cè)
????????????# 因?yàn)樗覀?cè)的滑動(dòng)框一定會(huì)向右移動(dòng)
????????????while?j < k and?window[j + 1] == window[j] + 1:
????????????????window[j] = j + 1
????????????????j += 1
????????????# 連續(xù)挨著最右側(cè)的滑動(dòng)框向右移動(dòng)一格
????????????window[j] += 1
????????????
????????return?ret
總結(jié)
上期推文：
評(píng)論
圖片
表情