棧 使用案例總結(jié)

最近有幾位球友問我，不知道怎么使用單調(diào)棧解決實際問題，今天我通過一道leetcode題目，來詳細解讀如何使用單調(diào)棧。

1 單調(diào)棧

單調(diào)棧是指棧內(nèi)元素組織有序的棧，分為單調(diào)遞增棧和單調(diào)遞減棧。

如下為單調(diào)遞增棧：

1->3->5->7

如下為單調(diào)遞減棧：

7->5->3->1

下面分析單調(diào)棧的應(yīng)用，節(jié)選自LeetCode

2 最大圓柱面積

給定 n 個非負整數(shù)，用來表示柱狀圖中各個柱子的高度。每個柱子彼此相鄰，且寬度為 1 。

求在該柱狀圖中，能夠勾勒出來的矩形的最大面積。

以上是柱狀圖的示例，其中每個柱子的寬度為 1，給定的高度為 [2,1,5,6,2,3]。

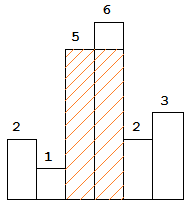
圖中陰影部分為所能勾勒出的最大矩形面積，其面積為 10 個單位。

示例:

輸入: [2,1,5,6,2,3]     輸出: 10

來源：力扣（LeetCode） 鏈接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram

3 為什么能用單調(diào)棧？

首先判斷能不能使用單調(diào)棧。若能，使用單調(diào)棧解決問題，需要找出棧內(nèi)存儲何值，何時入棧值，何時出棧值這三個問題。

因為勾勒出的圓柱中間不能出現(xiàn)任何空心，所以一旦出現(xiàn)如下駝峰結(jié)構(gòu)，便表明到以此局部極大值時，圓柱最大面積被找到，枚舉此局部區(qū)域所有可能的面積值，標記出最大值。

舉個例子說明上面的分析，如下結(jié)構(gòu)：

[2, 3, 5, 3]

此結(jié)構(gòu)在index=2時，達到局部極大值5，形成一個上面提到的駝峰結(jié)構(gòu)，且[2, 3, 5]是單調(diào)遞增的一側(cè)，index=2時達到頂峰，到index=2時，一定存在一個局部最大圓柱面積，可能的圓柱面積有：

height * width, 即：
5 * 1
3 * 2
2 * 3

即局部最大面積為 ：6

上面的分析恰好借助單調(diào)棧完美實現(xiàn)，為什么？第一，我們需要駝峰左側(cè)即單調(diào)遞增側(cè)，所以單調(diào)遞增棧能幫助我們做到。第二，單調(diào)遞增棧存儲元素的index，當前cur元素大于nums[stack[-1]]時入棧即可。

當前cur元素小于nums[stack[-1]]時，表明元素nums[stack[-1]]就是局部極大值，駝峰處index就是 stack[-1]，此時棧內(nèi)形成的就是駝峰左側(cè)單調(diào)遞增區(qū)域。

然后，我們逐次出棧stack，就是模擬上面的計算所有可能的圓柱面積，標記處局部極大面積即可。

所以單調(diào)遞增棧能夠完美實現(xiàn)我們的分析過程。

4 局部極大面積值

上面提到局部極大值，為什是局部極大面積值？因為我們從輸入列表heights中，可能找到多個駝峰。如下輸入：

[3, 4, 1, 5, 6, 3, 2, 5]

可能的駝峰結(jié)構(gòu)有：

[3, 4, 1]

[1, 5, 6, 3]

[3, 2, 5]

所以我們需要綜合考慮，上面每個駝峰結(jié)構(gòu)，并找出最大面積值。

5 偽代碼

    def largestRectangleArea(heights: List[int]) -> int:
        # 創(chuàng)建棧
        stack <- []
        # 遍歷heights
        for i in range(length):
            # 滿足while條件表明找到局部駝峰
            while stack is not empty and heights[i] smaller than stack top:
                # 逐次出棧
                p <- stack.pop(-1)
                # 找到一個可行解
                height, width <- heights[p], i-1-stack[-1] 
                s <- max(s, width*height)
            # 不滿足while條件，即要么stack為空，要么大于stack top
            stack.append(i)
            
        return s

6 用到哨兵

我們不能忽視對邊界情況的處理，對于如下單調(diào)遞增的輸入測試例子：

[3, 5, 7]

根據(jù)上面?zhèn)未a，元素會一直append到stack中，直到退出，返回圓柱面積s為0，這顯然是錯誤的。

如果在輸入列表heights尾部添加一個哨兵值0，問題會得到解決，因為輸入列表內(nèi)元素值都是正整數(shù)。添加0后，在index=2，元素7處必然達到駝峰，然后逐次出棧找到所有可能圓柱面積的最大值。

但是僅僅尾部添加一個哨兵值0就夠了嗎？注意觀察，若我們的輸入序列為如下，并且尾部添加一個哨兵值0：

[2, 1, 3, 5, 7, 0]

第一次進入while條件時，stack內(nèi)只有一個值（即index=0），執(zhí)行 p <- stack.pop(-1)出棧后，stack變?yōu)榭眨詓tack[-1]會拋出異常。為解決此問題，同樣在index=0處插入一個哨兵值0，作用為了防止拋出empty stack reference error

綜上所述，要在輸入列表heights兩頭各插入一個哨兵值0，便能完美解決上面兩個問題：

• 元素會一直append到stack中，直到退出，返回圓柱面積s為0，這顯然是錯誤的。
• empty stack reference error

7 完整代碼

如果理解上面的分析和兩個哨兵后，便不難看懂下面代碼：

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        length = len(heights)
        if length == 0:
            return 0
            
        stack, s = [], 0
        
        # 兩頭各插入1個哨兵
        heights.insert(0,0)
        heights.append(0) 
        length += 2

        for i in range(length):
           # 滿足while意味著找到一個駝峰     
            while len(stack)!=0 and heights[i]<heights[stack[-1]]:   
                p = stack.pop(-1)
                width = i - stack[-1] - 1
                height = heights[p]
                s = max(s, width * height)
            
            # 正在形成駝峰左側(cè)
            stack.append(i)
        
        return s