一篇文章帶你了解Python遞歸函數(shù)

回復(fù)“Go語(yǔ)言”即可獲贈(zèng)從入門到進(jìn)階共10本電子書

一、什么是遞歸函數(shù)？

在函數(shù)內(nèi)部，可以調(diào)用其他函數(shù)。如果一個(gè)函數(shù)在內(nèi)部調(diào)用自身本身，這個(gè)函數(shù)就是遞歸函數(shù)。

二、函數(shù)的遞歸調(diào)用原理

• 實(shí)際上遞歸函數(shù)是在棧內(nèi)存上遞歸執(zhí)行的，每次遞歸執(zhí)行一次就會(huì)耗費(fèi)一些棧內(nèi)存。

• 棧內(nèi)存的大小是限制遞歸深度的重要因素

三、案例分析

1. 求階乘

計(jì)算階乘n! = 1 x 2 x 3 x … x n，

可以用函數(shù)fact(n)表示。

fact(n) = n! = 1 x 2 x 3 x … x (n-1) x n = (n-1)! x n = fact(n-1) x n

fact(n)可以表示為n x fact(n-1)，只有n=1時(shí)需要特殊處理。

于是，fact(n)用遞歸的方式寫出來(lái)就是：

def fact(n):    if n == 1:        return 1    return n * fact(n - 1)

如果計(jì)算fact(6)，可以根據(jù)函數(shù)定義看到計(jì)算過(guò)程如下：

def fac(n):    if n==1:        return 1    else:        res=n*fac(n-1)        return  res
print(fac(6))

運(yùn)行結(jié)果：

2. 斐波拉契級(jí)數(shù)

有這樣一個(gè)數(shù)列：1，1，2，3，5，8，13，21，34…。其第一元素和第二個(gè)元素等于 1，其他元素等于其前面兩個(gè)元素的和。

例：

def fab(n):  # 定義斐波拉契級(jí)數(shù)    if n in [1, 2]:  # 如果n=1或者2      return 1    return fab(n - 1) + fab(n - 2)  # n>2

print(fab(1))  # 斐波拉契級(jí)數(shù)的第一個(gè)元素
print(fab(2))  # 斐波拉契級(jí)數(shù)的第二個(gè)元素
print(fab(8))  # 斐波拉契級(jí)數(shù)的第8個(gè)元素print(fab(13))  # 斐波拉契級(jí)數(shù)的第9個(gè)元素   

運(yùn)行結(jié)果：

3. 遞歸函數(shù)的優(yōu)點(diǎn)

定義簡(jiǎn)單，邏輯清晰。理論上，所有的遞歸函數(shù)都可以寫成循環(huán)的方式，但循環(huán)的邏輯不如遞歸清晰。

遞歸需要注意遞歸的深度。由于遞歸會(huì)產(chǎn)生多次函數(shù)調(diào)用，而函數(shù)調(diào)用會(huì)消耗代碼的棧空間，如果遞歸的深度太大，會(huì)導(dǎo)致棧溢出。以上面的階乘為例，如果計(jì)算 100000 的階乘，在一般機(jī)器上都會(huì)出現(xiàn)棧溢出的問(wèn)題。

print(fac(10000))

如下所示：

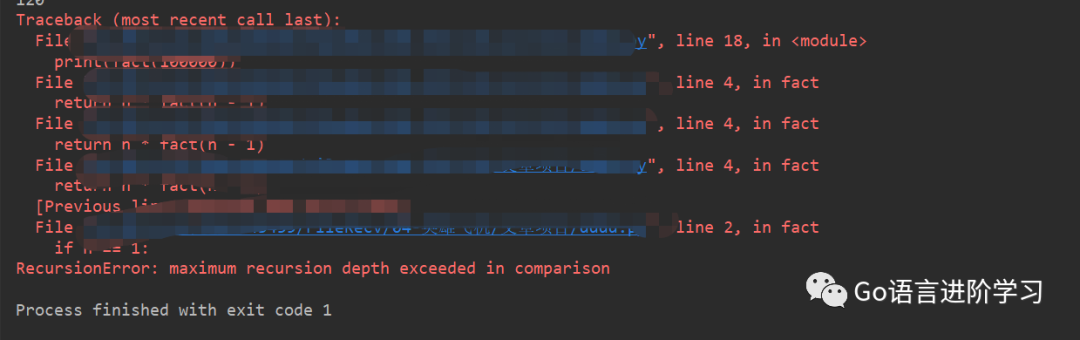
四、總結(jié)

本文基于Python基礎(chǔ)。Python標(biāo)準(zhǔn)的解釋器沒(méi)有針對(duì)尾遞歸做優(yōu)化，任何遞歸函數(shù)都存在棧溢出。介紹了在使用遞歸函數(shù)的優(yōu)缺點(diǎn)，優(yōu)點(diǎn)是邏輯簡(jiǎn)單清晰，缺點(diǎn)是過(guò)深的調(diào)用會(huì)導(dǎo)致棧溢出。

在實(shí)際案例中，針對(duì)尾遞歸優(yōu)化的語(yǔ)言可以通過(guò)尾遞歸防止棧溢出。尾遞歸事實(shí)上和循環(huán)是等價(jià)的，沒(méi)有循環(huán)語(yǔ)句的編程語(yǔ)言只能通過(guò)尾遞歸實(shí)現(xiàn)循環(huán)，進(jìn)行詳細(xì)的講解。

使用Python語(yǔ)言，希望能夠幫助你更好的學(xué)習(xí)。

------------------- End -------------------

往期精彩文章推薦：

• 從Go語(yǔ)言角度剖析關(guān)于計(jì)算機(jī)位的問(wèn)題

• 一篇文章帶你搞定Go語(yǔ)言基礎(chǔ)之文件操作

• 手把手教你用Go語(yǔ)言打造一款簡(jiǎn)易TCP端口掃描器

歡迎大家點(diǎn)贊，留言，轉(zhuǎn)發(fā)，轉(zhuǎn)載，感謝大家的相伴與支持

想加入Go學(xué)習(xí)群請(qǐng)?jiān)诤笈_(tái)回復(fù)【入群】

萬(wàn)水千山總是情，點(diǎn)個(gè)【在看】行不行