移動(dòng)矩陣的問題求解方法

題目介紹

最近練題的過程中，遇到這么一種情況：在一個(gè)二維矩陣中，有一個(gè)小的固定的圖形，需要移動(dòng)這個(gè)小的圖形到達(dá)某個(gè)指定的位置，求最短距離。

圖形化的題目看起來長下面這個(gè)樣子：

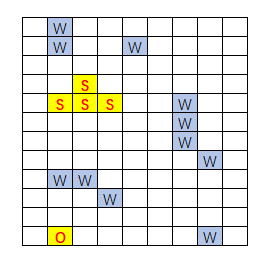
其中：

• ??S：表示起始位置

• ??O：表示目標(biāo)位置，S?接觸到?O?為終止條件

• ??W：表示水域，是不可通過的區(qū)域

這個(gè)圖還沒看明白題目的話，不要緊。看下面這張圖！！！

對滴！就是90坦克大戰(zhàn)的簡易版（暴露年齡，哈哈~），只不過我們題目的設(shè)定沒那么復(fù)雜，坦克也不能轉(zhuǎn)向。 下面就來看看代碼吧！

代碼實(shí)現(xiàn)

以下代碼僅表述核心算法邏輯，請忽略變量初始化等問題哈~

import?java.util.ArrayDeque;
import?java.util.ArrayList;
import?java.util.List;
import?java.util.Queue;

/**
?*?在一個(gè)二維矩陣中移動(dòng)固定圖案（一個(gè)小的矩陣，即多個(gè)元素的組合，其兩兩之間的相對位置不變）
?*?求其到位某個(gè)滿足條件位置的最小距離解法
?*/
public?class?MoveArray?{
????//?矩陣規(guī)模，R行C列
????static?int?R,?C;
????//?矩陣地圖
????static?char[][]?MAP;

????//?待移動(dòng)的圖形的點(diǎn)的集合
????static?List<int[]>?BODY;
????//?上下左右移動(dòng)的偏移量
????static?int[][]?MOVE?=?new?int[][]{{0,?1},?{0,?-1},?{1,?0},?{-1,?0}};

????static?Queue<List<int[]>>?QUEUE;
????static?List<int[]>?NEXT_ITEMS;
????static?boolean[][]?VISITED;

????static?int?ANS;

????/**
?????*?測試入口
?????*/
????public?static?void?main(String[]?args)?{
????????initData();
????????ANS?=?resolve();
????????System.out.println(ANS);
????}

????/**
?????*?初始化數(shù)據(jù)
?????*/
????private?static?void?initData()?{
????????MAP?=?new?char[R][C];
????????VISITED?=?new?boolean[R][C];
????????QUEUE?=?new?ArrayDeque<>();
????????NEXT_ITEMS?=?new?ArrayList<>();
????????ANS?=?0;

????????QUEUE.offer(BODY);
????????for?(int[]?cell?:?BODY)?{
????????????//?將指定的點(diǎn)的集合標(biāo)記為已訪問
????????????VISITED[cell[0]][cell[1]]?=?true;
????????}
????}

????/**
?????*?求解過程（標(biāo)準(zhǔn)BFS過程）
?????*?@return?最小距離（也可以直接用ANS，不用返回值）
?????*/
????private?static?int?resolve()?{
????????while?(!QUEUE.isEmpty())?{
????????????ANS++;
????????????while?(!QUEUE.isEmpty())?{
????????????????List<int[]>?body?=?QUEUE.poll();
????????????????for?(int[]?shift?:?MOVE)?{
????????????????????boolean[]?result?=?how(body,?shift);
????????????????????if?(!result[0])?{
????????????????????????//?當(dāng)前偏移不可達(dá)，繼續(xù)下一個(gè)偏移檢查
????????????????????????continue;
????????????????????}
????????????????????if?(result[1])?{
????????????????????????//?終止條件達(dá)成，返回當(dāng)前距離（最小距離）
????????????????????????return?ANS;
????????????????????}
????????????????????//?當(dāng)前偏移可通過，加入下一次偏移的集合
????????????????????List<int[]>?moved?=?new?ArrayList<>();
????????????????????for?(int[]?cell?:?body)?{
????????????????????????int?nx?=?cell[0]?+?shift[0];
????????????????????????int?ny?=?cell[1]?+?shift[1];

????????????????????????//?添加新的偏移后的點(diǎn)
????????????????????????moved.add(new?int[]{nx,?ny});
????????????????????????//?設(shè)置新的偏移點(diǎn)未已訪問
????????????????????????VISITED[nx][ny]?=?true;
????????????????????}
????????????????????NEXT_ITEMS.add(moved);
????????????????}
????????????}
????????????QUEUE.addAll(NEXT_ITEMS);
????????????NEXT_ITEMS.clear();
????????}
????????return?-1;
????}

????private?static?boolean[]?how(List<int[]>?body,?int[]?shift)?{
????????//?是否可達(dá)標(biāo)記
????????boolean?couldGo?=?false;
????????//?是否滿足終止條件標(biāo)記
????????boolean?touch?=?false;

????????for?(int[]?cell?:?body)?{
????????????int?nx?=?cell[0]?+?shift[0];
????????????int?ny?=?cell[1]?+?shift[1];
????????????if?(nx?>=?0?&&?nx?<?R?&&?ny?>=?0?&&?ny?<?C)?{
????????????????//?偏移的點(diǎn)在MAP范圍內(nèi)，進(jìn)一步判斷
????????????????if?('O'?==?MAP[nx][ny])?{
????????????????????//?滿足終止條件，變更標(biāo)記
????????????????????touch?=?true;
????????????????}
????????????????if?('W'?==?MAP[nx][ny])?{
????????????????????//?偏移后的點(diǎn)不可達(dá)，修改可達(dá)標(biāo)記，跳出
????????????????????//?因?yàn)橄乱粋€(gè)if的判斷，此處必須修改可達(dá)標(biāo)記！
????????????????????couldGo?=?false;
????????????????????break;
????????????????}
????????????????if?(!VISITED[nx][ny])?{
????????????????????//?任意一個(gè)偏移后的點(diǎn)未訪問，則認(rèn)為此次偏移后的整體未訪問過，修改可達(dá)標(biāo)記
????????????????????couldGo?=?true;
????????????????}
????????????}?else?{
????????????????//?偏移的點(diǎn)在MAP范圍外，該偏移不可達(dá)，跳出
????????????????couldGo?=?false;
????????????????break;
????????????}
????????}

????????return?new?boolean[]{couldGo,?touch};
????}
}

最后

以上算法就是對此類問題的個(gè)人理解，當(dāng)然這個(gè)算法思路在其他類似的模型中也能適用。如果您有更好的解法思路，請留言交流哈~

原文：https://www.jeremysong.cn/cn/move-array/

歡迎關(guān)注我的公眾號(hào)“須彌零一”，更多技術(shù)文章第一時(shí)間推送。