最短路問題與標號算法(label correcting algorithm)研究(4)

前文回顧
這是全文第三章label correcting algorithm的第二節(jié)。本章圍繞Label Correcting Algorithms展開。上一節(jié)已經介紹了最短路徑算法Generic Label Correcting Algorithm以及Modified Label Correcting Algorithm,本節(jié)將介紹在前兩個算法上改進得到的FIFO Label Correcting Algorithm以及Deque Label Correcting Algorithm。點擊下方鏈接回顧往期內容:
最短路問題與標號算法(label setting algorithm)研究(1) - 開篇介紹
最短路問題與標號算法(label correcting algorithm)研究(2) - 最短路徑問題簡介
最短路問題與標號算法(label correcting algorithm)研究(3)

3.4 FIFO Label Correcting Algorithm
3.4.1 算法介紹
同樣我們再次回顧一下Modified Label Correcting Algorithm的關鍵步驟:引入SE_LIST記錄距離標簽更新的節(jié)點編號,并在下一次迭代時檢查SE_LIST內某一節(jié)點發(fā)出的所有弧,即表3-5第7行與第13行。我們可以看出算法并沒有給出從SE_LIST中選擇節(jié)點以及向SE_LIST添加節(jié)點的具體規(guī)則,因此我們在相應代碼實現時以隨機的方式選取節(jié)點,并將新的節(jié)點添加到SE_LIST的尾部,即表3-6第48-50行與58-60行,表3-7第49-52行與63-65行。這種隨機方式是否會對算法效率產生影響呢?前邊我們已經知道,當最大網絡弧長非常大時Modified Label Correcting Algorithm的迭代次數為。現在假設我們其將應用到一個病態(tài)的數據集上(這類數據集往往含有非常大的值),且每次迭代時從SE_LIST中選取節(jié)點或向SE_LIST中添加節(jié)點的順序不合適時,算法總的迭代次數會隨著網絡節(jié)點數成指數式增長。顯然,為了保證算法效率的可靠性我們必須設計出較為合理的規(guī)則對SE_LIST中節(jié)點進行操作。這里介紹一種基于FIFO(FirstInFirstOut,先進先出)的節(jié)點處理規(guī)則,我們稱其為FIFO Label Correcting Algorithm。
這里我們嘗試對中的弧進行排序以解決Generic Label Correcting Algorithm中弧掃描規(guī)則不明確問題(或者說SE_LIST中節(jié)點操作順序問題):將弧集合中的所有弧以某種特定的方式排序,然后在每次迭代中逐個檢查中的弧,如果某條弧滿足條件:,則更新相應的距離標簽:,及節(jié)點的前向節(jié)點。當某步迭代后,中所有弧都滿足最優(yōu)性條件時,結束算法。接下來我們回顧一下3.3.1小節(jié)的內容,在引入SE_LIST時我們提到只有當節(jié)點的距離標簽更新時才需要在后續(xù)迭代時檢查從節(jié)點發(fā)出的所有弧是否滿足最優(yōu)性條件。所以上述嘗試還需進一步改進。我們將弧集合中的弧按照它們的尾節(jié)點升排序,以便所有具有相同尾節(jié)點的弧都連續(xù)出現在集合中。這樣在掃描弧時,我們可以一次考慮一個節(jié)點發(fā)出的所有弧,比如節(jié)點,掃描中的弧,并判斷其是否滿足最優(yōu)性條件。假設在某次迭代遍歷過程中,算法沒有更新節(jié)點的距離標簽,那么在下一步迭代中,始終存在,因此沒有必要再次檢查中的弧。根據以上分析,我們同樣引入可掃描列表SE_LIST,記錄在一次迭代過程中距離標簽發(fā)生更新的所有節(jié)點,并在下一次迭代中只考慮該列表中節(jié)點發(fā)出的所有弧。具體細節(jié)為:從SE_LIST一端(這里以左端為例)取出一個節(jié)點,檢查中的所有弧是否滿足最優(yōu)性條件;從SE_LIST另一端(右端)添加新的節(jié)點以便后續(xù)迭代檢查判斷。我們稱為FIFO規(guī)則,即先進先出。采用這類規(guī)則的算法稱為FIFO Label Correcting Algorithm,其算法步驟如下:
3.4.2 算法實現
首先給出Python版本的FIFO Label Correcting Algorithm實現(求解附錄2中源節(jié)點1到其他節(jié)點的最短路徑)。"""導入相關基礎包,定義全局變量"""表3-9 Python實現FIFO Label Correcting Algorithm(頁面可滑動)接下來給出MATLAB版本的FIFO Label Correcting Algorithm實現(求解附錄2中源節(jié)點1到其他節(jié)點的最短路徑)。
import?pandas?as?pd
import?numpy?as?np
import?copy
g_node_list=[]?#網絡節(jié)點集合
g_node_zone={}?#網絡節(jié)點類別集合
g_link_list=[]?#網絡弧集合
g_adjacent_arc_list={}#節(jié)點鄰接弧集合(從節(jié)點i發(fā)出的弧集合)
g_shortest_path=[]#最短路徑集合
g_node_status=[]#網絡節(jié)點狀態(tài)
g_number_of_nodes=0#網絡節(jié)點個數
g_origin=None???#網絡源節(jié)點
node_predecessor=[]#前向節(jié)點集合
node_label_cost=[]#距離標簽集合
SE_LIST=[]#可掃描節(jié)點集合
Max_label_cost=99999#初始距離標簽
"""導入網絡數據文件,構建基礎網絡并初始化相關變量"""
#讀取網絡節(jié)點數據
df_node=pd.read_csv('./input_file/node.csv')
df_node=df_node.iloc[:,:].values
for?i?in?range(len(df_node)):
????g_node_list.append(df_node[i,0])
????g_node_zone[df_node[i,?0]]?=?df_node[i,?-1]
????g_number_of_nodes+=1
????g_adjacent_arc_list[df_node[i,0]]=[]
????if?df_node[i,?3]?==?1:
????????g_origin?=?df_node[i,?0]
g_node_status=[0?for?i?in?range(g_number_of_nodes)]?#初始化網絡節(jié)點狀態(tài)
Distance=np.ones((g_number_of_nodes,g_number_of_nodes))\
*Max_label_cost?#距離矩陣
node_predecessor=[-1]*g_number_of_nodes
node_label_cost=[Max_label_cost]*g_number_of_nodes
node_predecessor[g_origin-1]=0
node_label_cost[g_origin-1]?=?0
#讀取網絡弧數據
df_link=pd.read_csv('./input_file/road_link.csv')
df_link=df_link.iloc[:,:].values
for?i?in?range(len(df_link)):
????g_link_list.append((df_link[i,1],df_link[i,2]))
????Distance[df_link[i,1]-1,df_link[i,2]-1]=df_link[i,3]
????g_adjacent_arc_list[df_link[i,1]].append(df_link[i,2])
SE_LIST=[g_origin]
g_node_status[g_origin-1]=1
"""最短路徑求解:掃描網絡弧,依據檢查最優(yōu)性條件更新距離標簽"""
while?len(SE_LIST):
????head=SE_LIST[0]#從可掃描列表中取出第一個元素
????SE_LIST.pop(0)#從可掃描列表中刪除第一個元素
????g_node_status[head-1]=0
????adjacent_arc_list=g_adjacent_arc_list[head]#獲取當前節(jié)點的鄰接弧集合
????for?tail?in?adjacent_arc_list:
????????if?node_label_cost[tail-1]>\
node_label_cost[head-1]+Distance[head-1,tail-1]:
????????????node_label_cost[tail-1]=\
node_label_cost[head-1]+Distance[head-1,tail-1]
????????????node_predecessor[tail-1]=head
????????????if?g_node_status[tail-1]==0:
????????????????SE_LIST.append(tail)#將新節(jié)點添加到可掃描列表尾部,append方法實現從列表尾部添加元素
????????????????g_node_status[tail-1]=1
"""依據前向節(jié)點生成最短路徑"""
agent_id=1
o_zone_id=g_node_zone[g_origin]
for?destination?in?g_node_list:
????if?g_origin!=destination:
????????d_zone_id=g_node_zone[destination]
????????if?node_label_cost[destination-1]==Max_label_cost:
????????????path="?"
????????????g_shortest_path.append([agent_id,?o_zone_id,d_zone_id,path,?node_label_cost[destination?-?1]])
????????else:
????????????to_node=copy.copy(destination)
????????????path=?"%s"?%?to_node
????????????while?node_predecessor[to_node-1]!=g_origin:
????????????????path="%s;"%?node_predecessor[to_node?-?1]?+?path
????????????????g=node_predecessor[to_node-1]
????????????????to_node=g
????????????path="%s;"%g_origin+path
????????????g_shortest_path.append([agent_id,?o_zone_id,d_zone_id,path,?node_label_cost[destination?-?1]])
????????agent_id+=1
"""將求解結果導出到csv文件"""
#將數據轉換為DataFrame格式方便導出csv文件
g_shortest_path=np.array(g_shortest_path)
col=['agent_id','o_zone_id','d_zone_id','node_sequence','distance']
file_data?=?pd.DataFrame(g_shortest_path,?index=range(len(g_shortest_path)),columns=col)
file_data.to_csv('./3_fifo_label_correcting/agent.csv',index=False)
%%?clear表3-10 MATLAB實現FIFO Label Correcting Algorithm(頁面可滑動)
clc
clear
%%?設置變量
g_node_list?=?[];?%網絡節(jié)點集合
g_link_list?=?[];?%網絡弧集合
g_origin?=?[];???%網絡源節(jié)點
g_number_of_nodes?=?0;%網絡節(jié)點個數
node_predecessor?=?[];%前向節(jié)點集合
node_label_cost?=?[];%距離標簽集合
Max_label_cost?=?inf;?%初始距離標簽
g_adjacent_arc_list={};?%節(jié)點鄰接弧集合(從節(jié)點i發(fā)出的弧集合)
g_node_status=[];?%網絡節(jié)點狀態(tài)
SE_LIST=[];?%可掃描節(jié)點集合
%%?導入網絡數據文件,構建基礎網絡并初始化相關變量
%讀取網絡節(jié)點數據
df_node?=?csvread('node.csv',1,0);
g_number_of_nodes?=?size(df_node,1);
g_node_list?=?df_node(:,1);
g_node_status?=?zeros(1,g_number_of_nodes);
for?i?=?1?:?g_number_of_nodes
????if?df_node(i,4)==1
????????g_origin=df_node(i,1);
????????o_zone_id?=?df_node(i,5);
????end
end
Distance?=?ones(g_number_of_nodes,g_number_of_nodes)*Max_label_cost;?
%距離矩陣
node_predecessor?=?-1*ones(1,g_number_of_nodes);
node_label_cost?=?Max_label_cost*ones(1,g_number_of_nodes);
node_predecessor(1,g_origin)?=?0;
node_label_cost(1,g_origin)?=?0;
g_adjacent_arc_list?=?cell(1,?g_number_of_nodes);
%讀取網絡弧數據
df_link?=?csvread('road_link.csv',1,0);
g_link_list?=?df_link(:,2:3);
for?i?=?1?:?size(df_link,?1)?
????Distance(df_link(i,2),df_link(i,3))?=?df_link(i,4);
????g_adjacent_arc_list{df_link(i,2)}?=?[g_adjacent_arc_list{df_link(i,2)},?df_link(i,3)];
end
%%?最短路徑求解:掃描網絡弧,依據檢查最優(yōu)性條件更新距離標簽
SE_LIST=[g_origin];
g_node_status(g_origin)=1;
while?~isempty(SE_LIST)
????head=SE_LIST(1);?%從可掃描列表中取出第一個元素
????SE_LIST(1)=[];?%從可掃描列表中刪除第一個元素
????g_node_status(head)=0;
adjacent_arc_list?=?g_adjacent_arc_list(head);?
%獲取當前節(jié)點的鄰接弧
????adjacent_arc_list?=?cell2mat(adjacent_arc_list);
????for?i?=?1?:?length(adjacent_arc_list)
????????tail?=?adjacent_arc_list(i);
????????if?node_label_cost(tail)>…
node_label_cost(head)+Distance(head,tail)
????????????node_label_cost(tail)=…
node_label_cost(head)+Distance(head,tail);
????????????node_predecessor(tail)=head;
????????????if?g_node_status(tail)==0
????????????????SE_LIST?=?[SE_LIST,tail];
????????????????g_node_status(tail)?=?1;
????????????end
????????end
????end???
end
%%?依據前向節(jié)點生成最短路徑
distance_column?=?[];
path_column?=?{};
o_zone_id_column?=?o_zone_id?*?ones(g_number_of_nodes-1,?1);
d_zone_id_column?=?[];
agent_id_column?=?[1:(g_number_of_nodes-1)]';
for?i?=?1:?size(g_node_list,?1)
????destination?=?g_node_list(i);
????if?g_origin?~=?destination
????????d_zone_id_column?=?[d_zone_id_column;?df_node(i,5)];
????????if?node_label_cost(destination)==Max_label_cost
????????????path="";
????????????distance?=?99999;
????????????distance_column?=?[distance_column;?99999];
????????else
????????????to_node=destination;
????????????path=num2str(to_node);
????????????while?node_predecessor(to_node)~=g_origin
????????????????path=strcat(';',path);
????????????????path=strcat(num2str(node_predecessor(to_node)),path);
????????????????g=node_predecessor(to_node);
????????????????to_node=g;
????????????end
????????????path=strcat(';',path);
????????????path=strcat(num2str(g_origin),path);
????????????distance_column?=?[distance_column;?node_label_cost(i)];
????????end
????????path_column=[path_column;path];
????end
end
title?=?{'agent_id','o_zone_id','d_zone_id','node_sequence','distance'};
result_table=table(agent_id_column,o_zone_id_column,…
d_zone_id_column,path_column,distance_column,'VariableNames',title);
writetable(result_table,?'agent.csv',…
'Delimiter',',','QuoteStrings',true)

3.5 Deque Label Correcting Algorithm
3.5.1算法介紹
同樣,我們先回顧一下已學的三個Label Correcting Algorithms的特點:Generic Label Correcting Algorithm提出了一種新的算法框架,即Label Correcting,它允許我們以更有效、靈活的方式求解最短路問題,但它的靈活性也正是它缺點,由于規(guī)則的缺失導致算法效率不能保證;因此Modified Label Correcting Algorithm引入了可掃描列表SE_LIST來明確應該掃描哪些弧,算法雖有改進但卻帶來了新的問題,以何種規(guī)則處理SE_LIST中節(jié)點?最后FIFO Label Correcting Algorithm提出了FIFO規(guī)則來明確SE_LIST中節(jié)點的操作規(guī)則,即表3-8第7行和第13行,在相應代碼實現中體現在表3-9第46-48行和第56-59行,表3-10第49-51行和第62-64行。這里請思考下除了FIFO是最好的么?還有其他規(guī)則可以選擇么?接下來我們介紹另一種規(guī)則:將SE_LIST作為Deque處理。如圖3-4(a)所示,Deuqe以Left-front標記隊列的左端頭部,Left-rear標記隊列的左端尾部,Right-front標記隊列的右端頭部,Right-rear標記隊列的右端尾部,當需要進行刪除或者插入操作時可以選擇在兩端進行。
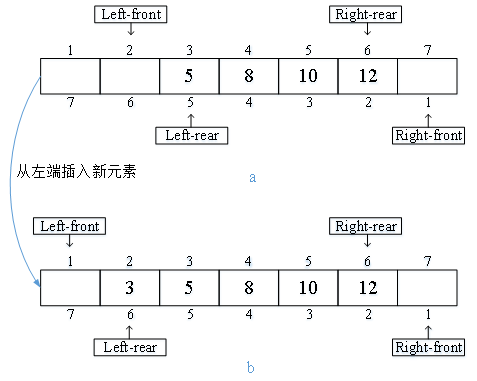

復雜度分析大量研究表明,Deque方法檢查的節(jié)點數量比大多數其他標簽校正算法要少。雖然該算法時間復雜度不是多項式,但在實際應用中卻很有效。而且,該算法被證明是解決稀疏和交通網絡最短路問題最快的算法之一。
3.5.2 算法實現
"""導入相關基礎包,定義全局變量"""表3-12 Python實現Deque Label Correcting Algorithm(頁面可滑動)接下來給出MATLAB版本的Deque Label Correcting Algorithm實現(求解附錄2中源節(jié)點1到其他節(jié)點的最短路徑)。
import?pandas?as?pd
import?numpy?as?np
import?copy
g_node_list=[]?#網絡節(jié)點集合
g_node_zone={}?#網絡節(jié)點類別集合
g_link_list=[]?#網絡弧集合
g_adjacent_arc_list={}#節(jié)點鄰接弧集合(從節(jié)點i發(fā)出的弧集合)
g_shortest_path=[]#最短路徑集合
g_node_status=[]#網絡節(jié)點狀態(tài)
g_number_of_nodes=0#網絡節(jié)點個數
g_origin=None???#網絡源節(jié)點
node_predecessor=[]#前向節(jié)點集合
node_label_cost=[]#距離標簽集合
SE_LIST=[]#可掃描節(jié)點集合
Max_label_cost=99999#初始距離標簽
"""導入網絡數據文件,構建基礎網絡并初始化相關變量"""
#讀取網絡節(jié)點數據
df_node=pd.read_csv('./input_file/node.csv')
df_node=df_node.iloc[:,:].values
for?i?in?range(len(df_node)):
????g_node_list.append(df_node[i,0])
????g_node_zone[df_node[i,?0]]?=?df_node[i,?-1]
????g_number_of_nodes+=1
????g_adjacent_arc_list[df_node[i,0]]=[]
????if?df_node[i,?3]?==?1:
????????g_origin?=?df_node[i,?0]
g_node_status=[0?for?i?in?range(g_number_of_nodes)]?#初始化網絡節(jié)點狀態(tài)
Distance=np.ones((g_number_of_nodes,g_number_of_nodes))\
*Max_label_cost?#距離矩陣
node_predecessor=[-1]*g_number_of_nodes
node_label_cost=[Max_label_cost]*g_number_of_nodes
node_predecessor[g_origin-1]=0
node_label_cost[g_origin-1]?=?0
#讀取網絡弧數據
df_link=pd.read_csv('./input_file/road_link.csv')
df_link=df_link.iloc[:,:].values
for?i?in?range(len(df_link)):
????g_link_list.append((df_link[i,1],df_link[i,2]))
????Distance[df_link[i,1]-1,df_link[i,2]-1]=df_link[i,3]
????g_adjacent_arc_list[df_link[i,1]].append(df_link[i,2])
SE_LIST=[g_origin]
g_node_status[g_origin-1]=1
"""最短路徑求解:掃描網絡弧,依據檢查最優(yōu)性條件更新距離標簽"""
while?len(SE_LIST):
????head=SE_LIST[0]#從可掃描列表中取出第一個元素
????SE_LIST.pop(0)#從可掃描列表中刪除第一個元素
????g_node_status[head-1]=0
????adjacent_arc_list=g_adjacent_arc_list[head]#獲取當前節(jié)點的鄰接弧集合
????for?tail?in?adjacent_arc_list:
????????if?node_label_cost[tail-1]>\
node_label_cost[head-1]+Distance[head-1,tail-1]:
????????????node_label_cost[tail-1]=\
node_label_cost[head-1]+Distance[head-1,tail-1]
????????????node_predecessor[tail-1]=head
????????????if?g_node_status[tail-1]==0:
????????????????SE_LIST.append(tail)#將新節(jié)點添加到可掃描列表尾部,append方法實現從列表尾部添加元素
????????????????g_node_status[tail-1]=1
"""依據前向節(jié)點生成最短路徑"""
agent_id=1
o_zone_id=g_node_zone[g_origin]
for?destination?in?g_node_list:
????if?g_origin!=destination:
????????d_zone_id=g_node_zone[destination]
????????if?node_label_cost[destination-1]==Max_label_cost:
????????????path="?"
????????????g_shortest_path.append([agent_id,?o_zone_id,d_zone_id,path,?node_label_cost[destination?-?1]])
????????else:
????????????to_node=copy.copy(destination)
????????????path=?"%s"?%?to_node
????????????while?node_predecessor[to_node-1]!=g_origin:
????????????????path="%s;"%?node_predecessor[to_node?-?1]?+?path
????????????????g=node_predecessor[to_node-1]
????????????????to_node=g
????????????path="%s;"%g_origin+path
????????????g_shortest_path.append([agent_id,?o_zone_id,d_zone_id,path,?node_label_cost[destination?-?1]])
????????agent_id+=1
"""將求解結果導出到csv文件"""
#將數據轉換為DataFrame格式方便導出csv文件
g_shortest_path=np.array(g_shortest_path)
col=['agent_id','o_zone_id','d_zone_id','node_sequence','distance']
file_data?=?pd.DataFrame(g_shortest_path,?index=range(len(g_shortest_path)),columns=col)
file_data.to_csv('./3_fifo_label_correcting/agent.csv',index=False)
%%?clear表3-13 MATLAB實現Deque Label Correcting Algorithm(頁面可滑動)
clc
clear
%%?設置變量
g_node_list?=?[];?%網絡節(jié)點集合
g_link_list?=?[];?%網絡弧集合
g_origin?=?[];???%網絡源節(jié)點
g_number_of_nodes?=?0;%網絡節(jié)點個數
node_predecessor?=?[];%前向節(jié)點集合
node_label_cost?=?[];%距離標簽集合
Max_label_cost?=?inf;?%初始距離標簽
g_adjacent_arc_list={};?%節(jié)點鄰接弧集合(從節(jié)點i發(fā)出的弧集合)
g_node_status=[];?%網絡節(jié)點狀態(tài)
SE_LIST=[];?%可掃描節(jié)點集合
%%?導入網絡數據文件,構建基礎網絡并初始化相關變量
%讀取網絡節(jié)點數據
df_node?=?csvread('node.csv',1,0);
g_number_of_nodes?=?size(df_node,1);
g_node_list?=?df_node(:,1);
g_node_status?=?zeros(1,g_number_of_nodes);
for?i?=?1?:?g_number_of_nodes
????if?df_node(i,4)==1
????????g_origin=df_node(i,1);
????????o_zone_id?=?df_node(i,5);
????end
end
Distance?=?ones(g_number_of_nodes,g_number_of_nodes)*Max_label_cost;?
%距離矩陣
node_predecessor?=?-1*ones(1,g_number_of_nodes);
node_label_cost?=?Max_label_cost*ones(1,g_number_of_nodes);
node_predecessor(1,g_origin)?=?0;
node_label_cost(1,g_origin)?=?0;
g_adjacent_arc_list?=?cell(1,?g_number_of_nodes);
%讀取網絡弧數據
df_link?=?csvread('road_link.csv',1,0);
g_link_list?=?df_link(:,2:3);
for?i?=?1?:?size(df_link,?1)?
????Distance(df_link(i,2),df_link(i,3))?=?df_link(i,4);
????g_adjacent_arc_list{df_link(i,2)}?=?[g_adjacent_arc_list{df_link(i,2)},?df_link(i,3)];
end
%%?最短路徑求解:掃描網絡弧,依據檢查最優(yōu)性條件更新距離標簽
SE_LIST=[g_origin];
g_node_status(g_origin)=1;
while?~isempty(SE_LIST)
????head=SE_LIST(1);?%從可掃描列表中取出第一個元素
????SE_LIST(1)=[];?%從可掃描列表中刪除第一個元素
????g_node_status(head)?=?2;
adjacent_arc_list?=?g_adjacent_arc_list(head);?
%獲取當前節(jié)點的鄰接弧
????adjacent_arc_list?=?cell2mat(adjacent_arc_list);
????for?i?=?1?:?length(adjacent_arc_list)
????????tail?=?adjacent_arc_list(i);
????????if?node_label_cost(tail)>…
node_label_cost(head)+Distance(head,tail)
????????????node_label_cost(tail)=…
node_label_cost(head)+Distance(head,tail);
????????????node_predecessor(tail)=head;
????????????if?g_node_status(tail)==0
????????????????SE_LIST?=?[SE_LIST,?tail];
????????????????g_node_status(tail)?=?1;
????????????elseif?g_node_status(tail)?==?2
????????????????SE_LIST?=?[tail,?SE_LIST];
????????????????g_node_status(tail)?=?1;
????????????end
????????end
????end???
end
%%?依據前向節(jié)點生成最短路徑
destination_column?=?[];
distance_column?=?[];
path_column?=?{};
o_zone_id_column?=?o_zone_id?*?ones(g_number_of_nodes-1,?1);
d_zone_id_column?=?[];
agent_id_column?=?[1:(g_number_of_nodes-1)]';
for?i?=?1:?size(g_node_list,?1)
????destination?=?g_node_list(i);
????if?g_origin?~=?destination
????????destination_column?=?[destination_column;?destination];
????????d_zone_id_column?=?[d_zone_id_column;?df_node(i,5)];
????????if?node_label_cost(destination)==Max_label_cost
????????????path="";
????????????distance?=?99999;
????????????distance_column?=?[distance_column;?99999];
????????else
????????????to_node=destination;
????????????path=num2str(to_node);
????????????while?node_predecessor(to_node)~=g_origin
????????????????path=strcat(';',path);
????????????????path=strcat(num2str(node_predecessor(to_node)),path);
????????????????g=node_predecessor(to_node);
????????????????to_node=g;
????????????end
????????????path=strcat(';',path);
????????????path=strcat(num2str(g_origin),path);
????????????distance_column?=?[distance_column;?node_label_cost(i)];
????????end
????????path_column=[path_column;path];
????end
end
title?=?{'agent_id','o_zone_id','d_zone_id','node_sequence','distance'};
result_table=table(agent_id_column,o_zone_id_column,…
d_zone_id_column,path_column,distance_column,'VariableNames',title);
writetable(result_table,?'agent.csv',…
'Delimiter',',','QuoteStrings',true)
欲下載本文代碼資料,請移步留言區(qū)
周學松教授?是亞利桑那州立大學(ASU)可持續(xù)工程與建筑環(huán)境學院教授,目前是Transportation Research Part C的副主編,城市軌道交通urbanrail transit 執(zhí)行主編,Transportation Research Part B的編委。主要研究大規(guī)模多模式交通系統優(yōu)化和仿真算法。
文案&編輯:崔贊揚、李崇楠(北京交通大學)審稿人:鄧發(fā)珩、周航、向柯瑋(華中科技大學管理學院)指導老師:周學松(Arizona State University)如對文中內容有疑問,歡迎交流。(PS:部分資料來自網絡)
如有需求,可以聯系:崔贊揚(北京交通大學博士:[email protected])李崇楠(北京交通大學本科:[email protected])周學松(Arizona State University Professor:? [email protected])鄧發(fā)珩(華中科技大學本科三年級:? [email protected]、個人公眾號:程序猿聲)周航(華中科技大學本科一年級:[email protected])向柯瑋(華中科技大學本科一年級:[email protected])排版:程欣悅([email protected])
推薦閱讀:
干貨 | 學習算法,你需要掌握這些編程基礎(包含JAVA和C++)
記得點個在看支持下哦~

評論
圖片
表情
