70 張圖帶你徹底掌握紅黑樹(shù)!

前言

紅黑樹(shù)是工程中一種非常重要的數(shù)據(jù)結(jié)構(gòu)，大家熟悉的 HashMap 在 Java 8 就引入了紅黑樹(shù)的數(shù)據(jù)結(jié)構(gòu)，不過(guò)實(shí)話實(shí)說(shuō)，紅黑樹(shù)確實(shí)不容易掌握，左旋，右旋等概念讓人頭發(fā)發(fā)麻，本文用圖文并茂的形式以期讓讀者徹底掌握紅黑樹(shù)，希望大家看了有收獲，這篇文章肝了十多天，非常不易，希望大家不要白嫖，三連走起，多謝支持!

開(kāi)篇我們先來(lái)聊一聊和樹(shù)相關(guān)的一些概念，來(lái)一步一步引入為什么要使用紅黑樹(shù)。這樣能夠讓大家知其然而知其所以然，最后你會(huì)發(fā)現(xiàn)，紅黑樹(shù)的處理情況也就那幾種，甚至可以說(shuō)就固定那幾種情況，多看看我的分析就能拿下了。話不多話，我們先從樹(shù)的概念開(kāi)始。

友情提示：本文篇幅比較長(zhǎng)，但是總體而言簡(jiǎn)單易懂，還請(qǐng)各位坐穩(wěn)。

1、樹(shù)

樹(shù)的定義如下

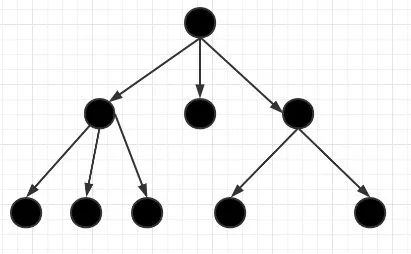
樹(shù)是一種非線性的數(shù)據(jù)結(jié)構(gòu)，它是由n（n>=0）個(gè)有限節(jié)點(diǎn)組成一個(gè)具有層次關(guān)系的集合。把它叫做樹(shù)是因?yàn)樗雌饋?lái)像一棵倒掛的樹(shù)，也就是說(shuō)它是根朝上，而葉朝下的。它具有以下的特點(diǎn)：

1.每個(gè)節(jié)點(diǎn)有零個(gè)或多個(gè)子節(jié)點(diǎn)；

2.沒(méi)有父節(jié)點(diǎn)的節(jié)點(diǎn)稱(chēng)為根節(jié)點(diǎn)；

3.每一個(gè)非根節(jié)點(diǎn)有且只有一個(gè)父節(jié)點(diǎn)；

4.除了根節(jié)點(diǎn)外，每個(gè)子節(jié)點(diǎn)可以分為多個(gè)不相交的子樹(shù)

樹(shù)的一些重要的名詞解釋

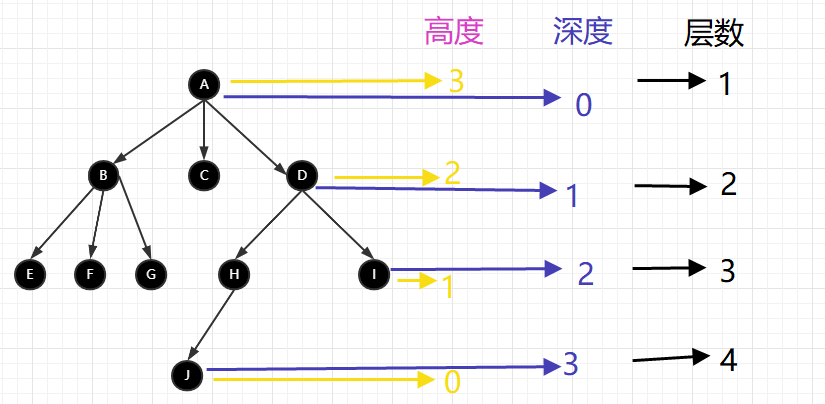
1.?高度：當(dāng)前節(jié)點(diǎn)到葉子節(jié)點(diǎn)的最長(zhǎng)路徑?
2.?深度：根節(jié)點(diǎn)到當(dāng)前節(jié)點(diǎn)經(jīng)過(guò)的邊數(shù)?
3.?層數(shù)：節(jié)點(diǎn)的深度+1 樹(shù)的高度：即根節(jié)點(diǎn)的高度（就是根節(jié)點(diǎn)到葉子節(jié)點(diǎn)的最長(zhǎng)路徑）?
4.?父節(jié)點(diǎn)：若一個(gè)節(jié)點(diǎn)含有子節(jié)點(diǎn)，則這個(gè)節(jié)點(diǎn)稱(chēng)為其子節(jié)點(diǎn)的父節(jié)點(diǎn)?
5.?子節(jié)點(diǎn)：一個(gè)節(jié)點(diǎn)包含的子樹(shù)節(jié)點(diǎn)?
6.?兄弟節(jié)點(diǎn)：具有相同父節(jié)點(diǎn)的節(jié)點(diǎn)稱(chēng)為兄弟節(jié)點(diǎn)?
7.?葉節(jié)點(diǎn)：沒(méi)有子節(jié)點(diǎn)的節(jié)點(diǎn)（也叫頁(yè)子節(jié)點(diǎn)）?以上是關(guān)于樹(shù)的一些常見(jiàn)的概念

（其他的一些概念不是很重要就不一一列出來(lái)了。）

來(lái)結(jié)合一張圖來(lái)更直觀的理解下上面的各個(gè)名詞的好含義

2、二叉樹(shù)

二叉樹(shù)的定義:樹(shù)的每個(gè)節(jié)點(diǎn)最多有兩個(gè)子節(jié)點(diǎn)

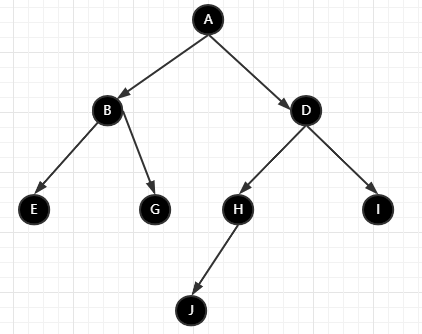
雖然 H 節(jié)點(diǎn)只有一個(gè)子節(jié)點(diǎn)，但是它也是一個(gè)二叉樹(shù)，因?yàn)闈M足最多只有個(gè)兩個(gè)子節(jié)點(diǎn)

3、二叉搜索樹(shù)

二叉搜索樹(shù)其實(shí)就是二叉樹(shù)，只不過(guò)又有一些額外的條件限制。其額外條件如下：

① 若它的左子樹(shù)不為空，那么左子樹(shù)上面的所有節(jié)點(diǎn)的值均小于它的根節(jié)點(diǎn)的值

② 若它的右子樹(shù)不為空，那么右子樹(shù)上面的所有的節(jié)點(diǎn)的值均大于它的根節(jié)點(diǎn)的值

③ 它的左右的樹(shù)葉分別為二叉排序樹(shù)

其中重點(diǎn)強(qiáng)調(diào)下二叉搜索樹(shù)的中序遍歷（因?yàn)檫@是最常見(jiàn)的）。中序遍歷的規(guī)則是：先遍歷左子樹(shù)，再遍歷根節(jié)點(diǎn)，然后遍歷右子樹(shù)

例如下面這個(gè)二叉搜索樹(shù)的遍歷的結(jié)果：D-H-B-E-A-F-C-G

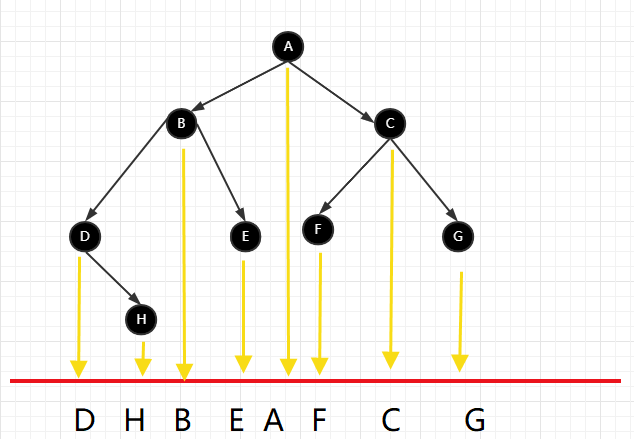
如果從A的上面使用一個(gè)光源往下照，那么整個(gè)樹(shù)的節(jié)點(diǎn)在地面上的投影其實(shí)就是中序遍歷的結(jié)果。二叉搜索樹(shù)的時(shí)間復(fù)雜度是 O（logn）

下面我們?cè)賮?lái)一起看下二叉搜索樹(shù)的查找某個(gè)節(jié)點(diǎn)的算法（詳細(xì)步驟全部使用注釋寫(xiě)清楚了，因?yàn)榧t黑樹(shù)就是基于二分查找樹(shù)的，所以這里就多提一筆）

public?class?BinaryTreeDemo?{
????public?static?void?main(String[]?args)?{
????????//前提這必須是一個(gè)有序的數(shù)組，否則是無(wú)法使用二分查找的
????????Integer[]?searchArr?=?{1,?2,?3,?5,?6,?7,?9,?11,?23,?45,?67,?89};
????????//假設(shè)要查找?3?這個(gè)數(shù)據(jù)
????????Integer?index?=?binarySearchTree(searchArr,?3);
????????System.out.println("index?=?"?+?index);
????}

????private?static?Integer?binarySearchTree(Integer[]?searchArr,?int?searchData)?{
????????//定義數(shù)組的低位的索引
????????int?lowBit?=?0;
????????//定義數(shù)組的高位的索引
????????int?heightBit?=?searchArr.length?-?1;
????????//(heightBit?-?lowBit)?/?2?得到的是兩個(gè)位置的中間位置，再加上?low?就是實(shí)際的?heightBit?和?lowBit?的中間位置
????????//不懂的不用太糾結(jié)，重點(diǎn)是紅黑樹(shù)
????????while?(lowBit?<=?heightBit)?{
????????????//這里為什么這么定義中間位置
????????????//因?yàn)?（heightBit?-?lowBit）/2?結(jié)果是兩者的相對(duì)中間點(diǎn)，再加上lowBit?其實(shí)就是高位和低位的中間位置
????????????//這里如果實(shí)在想不明白就去畫(huà)畫(huà)圖，記住，不能寫(xiě)成（heightBit?+?lowBit）/2
????????????int?midBit?=?lowBit?+?(heightBit?-?lowBit)?/?2;
????????????//開(kāi)始二分查找
????????????//如果被查找的數(shù)據(jù)組的中間位置的值?小于?要搜索的值
????????????//說(shuō)明?searchData?在中間位置的右邊
????????????if?(searchArr[midBit]?????????????????//這里為什么要?+ 1 ？
????????????????//?因?yàn)閙idBit?位置已經(jīng)確定比?searchData?小了，所以需要從midBit的下一個(gè)索引位置開(kāi)始繼續(xù)找
????????????????//?也就是說(shuō)?將?midBit?及?midBit?的左邊的部分砍掉
????????????????lowBit?=?midBit?+?1;
????????????}?else?if?(searchArr[midBit]?==?searchData)?{
????????????????return?midBit;
????????????}?else?{
????????????????//這里的作用和?第一個(gè)?if中的類(lèi)似
????????????????//因?yàn)橐檎业?searchData?
????????????????//也就是說(shuō)?直接將?midBit?及?midBit?右邊的部分砍掉
????????????????heightBit?=?midBit?-?1;
????????????}
????????}
????????return?null;
????}
}

二分查找樹(shù)的最大的缺點(diǎn)是依賴(lài)有序數(shù)組，而數(shù)組的缺點(diǎn)就是不能擴(kuò)容，還有就是在添加和刪除元素的時(shí)候需要移動(dòng)數(shù)組，性能不理想。上面我們還說(shuō)過(guò)一個(gè)問(wèn)題，就是二叉樹(shù)的特點(diǎn)就是每個(gè)節(jié)點(diǎn)的最多只有兩個(gè)子節(jié)點(diǎn)，結(jié)合二叉搜索樹(shù)的特點(diǎn)就是 左子節(jié)點(diǎn) < 根節(jié)點(diǎn) < 右子節(jié)點(diǎn)，那么在極端情況下，可能會(huì)出現(xiàn)下面這樣的情況

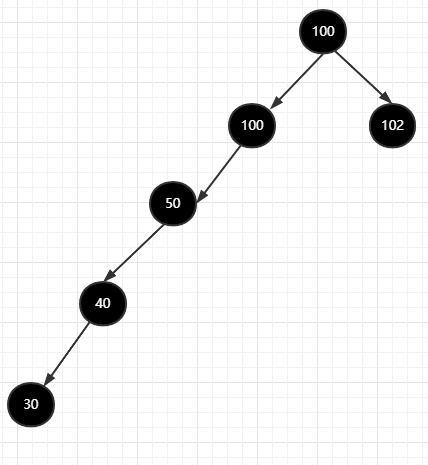
在這種極端的情況下，可能會(huì)出現(xiàn)這種線性樹(shù)結(jié)構(gòu)，基本退化成鏈表了，那時(shí)間復(fù)雜度就變成了 O(n)。這個(gè)時(shí)間復(fù)雜度也太不穩(wěn)定了，這種不穩(wěn)定的東西在系統(tǒng)中就是定時(shí)炸彈。所以二叉搜索樹(shù)被進(jìn)一步的優(yōu)化成 AVL 樹(shù)

4、AVL 樹(shù)

#?AVL?樹(shù)的定義（AVL?是兩個(gè)人的名字的簡(jiǎn)稱(chēng)，是這兩個(gè)人發(fā)明的）
具有二叉搜索樹(shù)的全部特點(diǎn)，并且沒(méi)有節(jié)點(diǎn)的左右節(jié)點(diǎn)的高度相差至多等于1（高度相差不能大于1這個(gè)就嚴(yán)格限制死了?AVL?樹(shù)，導(dǎo)致其實(shí)際應(yīng)用場(chǎng)景并不是很多）

AVL 樹(shù)也叫平衡二叉樹(shù)，他的時(shí)間復(fù)雜度是 O(logn)

AVL 的左右樹(shù)的高度差也叫平衡因子（平衡因子就是從某個(gè)節(jié)點(diǎn)開(kāi)始，他的左右子樹(shù)的節(jié)點(diǎn)數(shù)差），即平衡因子不大于 1。

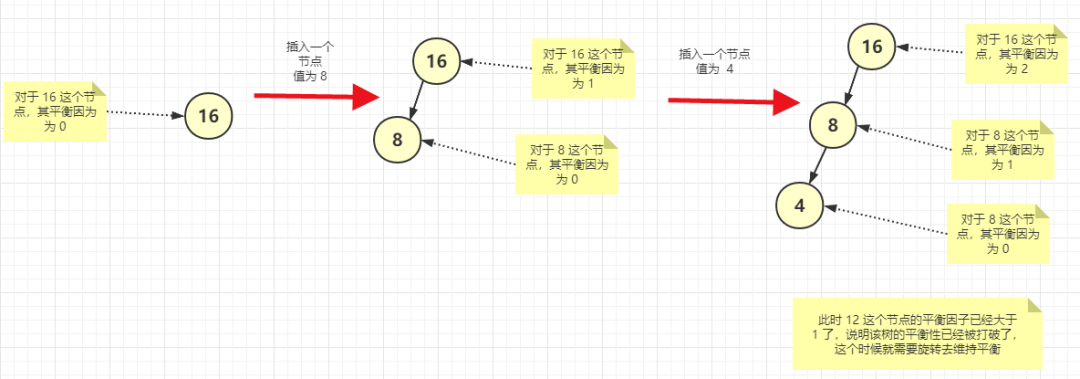
但實(shí)際情況是根本不可能插入的數(shù)據(jù)這么巧的剛好一大一小的在左右樹(shù)插入，所以 AVL 樹(shù)在插入數(shù)據(jù)的時(shí)候會(huì)不斷地調(diào)整，因?yàn)楦叨认嗖畈淮笥?1 真的太嚴(yán)格了。那這樣在頻繁插入的時(shí)候必然需要一直調(diào)整樹(shù)的結(jié)構(gòu)，讓其保持平衡。如下圖（假設(shè)現(xiàn)在插入的不平衡的節(jié)點(diǎn)在左側(cè)）

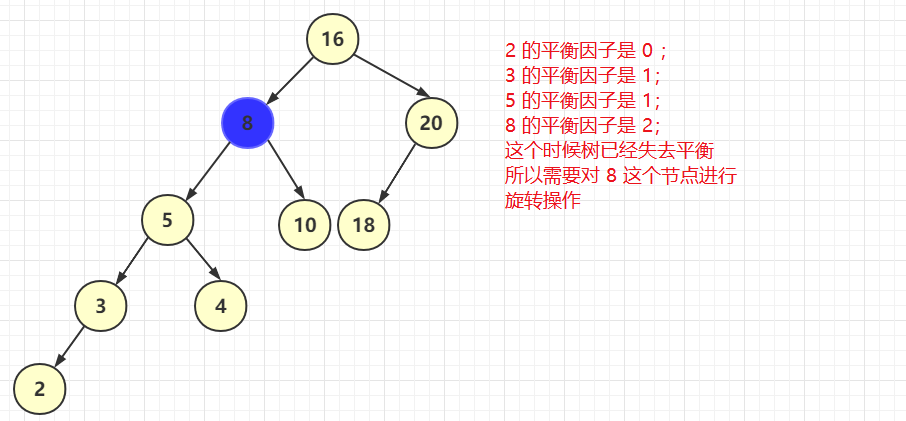
此時(shí)這種情況稱(chēng)之為左失衡，所以很顯然需要進(jìn)行右旋轉(zhuǎn)（具體旋轉(zhuǎn)會(huì)在紅黑樹(shù)中在介紹），右失衡的情況和此類(lèi)似。可想而知不斷地調(diào)整會(huì)導(dǎo)致性能低下。

說(shuō)到這里，是不是機(jī)智的你也發(fā)現(xiàn)了樹(shù)為啥會(huì)一步一步的進(jìn)化演變，主要還是因?yàn)橐延械墓δ軣o(wú)法滿足新的需求，才會(huì)開(kāi)始尋找新的解決辦法。這就像架構(gòu)一樣，一開(kāi)始是單體應(yīng)用，隨著業(yè)務(wù)量的提升，逐漸演變?yōu)榱宋⒎?wù)架構(gòu)。結(jié)合當(dāng)前業(yè)務(wù)不斷優(yōu)化現(xiàn)有技術(shù)棧，才是架構(gòu)的本質(zhì)

5、2-3樹(shù)

有的小伙伴可能已經(jīng)不耐煩了，怎么說(shuō)好的紅黑樹(shù)，說(shuō)半天還沒(méi)到紅黑樹(shù)，難不成你是在摸魚(yú)？

事實(shí)上如果上來(lái)就是紅黑樹(shù)我估計(jì)我自己看的都發(fā)懵，之所以一個(gè)又一個(gè)的鋪墊，主要目的還是想讓小伙伴們能有一次性拿下紅黑樹(shù)（手動(dòng)滑稽）。好了，我們來(lái)繼續(xù)說(shuō) 2-3 樹(shù)，2-3 樹(shù)的特點(diǎn)是什么？它能夠維持絕對(duì)的平衡，下面我們來(lái)演示下 2-3 樹(shù)添加節(jié)點(diǎn)的過(guò)程

#?2-3?樹(shù)的特點(diǎn)
1.?2-3樹(shù)?是平衡樹(shù)?
2.?2?叉節(jié)點(diǎn)，有兩個(gè)分樹(shù)，節(jié)點(diǎn)中有一個(gè)元素，左樹(shù)元素更小，右樹(shù)元素節(jié)點(diǎn)更大?
3.?3?叉節(jié)點(diǎn)，有三個(gè)子樹(shù)，節(jié)點(diǎn)中有兩個(gè)元素，左樹(shù)元素更小，右樹(shù)元素更大，中間樹(shù)介于兩個(gè)父元素之間

① 假設(shè)現(xiàn)在有一個(gè)節(jié)點(diǎn) 40，那啥也別說(shuō)了，第一個(gè)節(jié)點(diǎn)啥都不做，老實(shí)呆著就行；

② 下一個(gè)節(jié)點(diǎn) 35 ，先從根節(jié)點(diǎn)開(kāi)始，發(fā)現(xiàn) 40 > 35 ，此時(shí)理論上 35 應(yīng)該添加到 40 的左子樹(shù)上，但是對(duì)于 2-3 樹(shù)，并不是你想的那樣子，記住核心的一句話對(duì)于 2-3 樹(shù)的添加，永遠(yuǎn)不會(huì)添加到一個(gè)空的節(jié)點(diǎn)去，只會(huì)跟最后找到的葉子節(jié)點(diǎn)做融合（不明白也沒(méi)事，先把這個(gè)過(guò)程看完），那添加到哪里？實(shí)際上他們會(huì)這樣存儲(chǔ)：

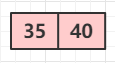
現(xiàn)在這個(gè)變成了一個(gè) 3 節(jié)點(diǎn)。此時(shí)這顆樹(shù)依舊是平衡的。

#?怎么理解這個(gè)?3?節(jié)點(diǎn)
因?yàn)榻酉聛?lái)的數(shù)據(jù)可能是小于 35 ，可能是在 35 到 40?之間，也可能是大于 40?的，所以這個(gè)節(jié)點(diǎn)能放三個(gè)節(jié)點(diǎn)，這就是 3 節(jié)點(diǎn)的含義

③ 下一個(gè)節(jié)點(diǎn)是 12 ，按照我們上面解釋的 3 節(jié)點(diǎn)的含義，那既然 12 < 35 那是不是就是這樣子的呢？

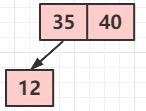
很顯然不是，不要忘記了上面的那句核心的話（對(duì)于 2-3 樹(shù)的添加，永遠(yuǎn)不會(huì)添加到一個(gè)空的節(jié)點(diǎn)去，只會(huì)跟最后找到的葉子節(jié)點(diǎn)做融合），因?yàn)榇藭r(shí) 35 的左子節(jié)點(diǎn)是空，所以 12 是不可能添加進(jìn)去的，實(shí)際上他是這么添加的

那這個(gè)時(shí)候按照 3 節(jié)點(diǎn)的定義，那這個(gè)豈不是 4 節(jié)點(diǎn)了？其實(shí)這個(gè)時(shí)候答案已經(jīng)很明顯了，就是此時(shí)該樹(shù)會(huì)分裂成一個(gè)正常的二叉樹(shù)，也就是這樣子的，這棵樹(shù)依舊是覺(jué)得平衡

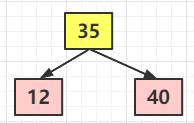
④ 繼續(xù)添加節(jié)點(diǎn) 18 ，自己能腦補(bǔ)下該怎么添加嗎？這時(shí)候就很簡(jiǎn)單了，18 < 35 ，就添加到左子節(jié)點(diǎn)，此時(shí)左子節(jié)點(diǎn)不為空，那么就可以繼續(xù)添加，而 18 > 12，理論上應(yīng)該是添加到 12 的右子節(jié)點(diǎn)，但是由于對(duì)于 2-3 樹(shù)的添加，永遠(yuǎn)不會(huì)添加到一個(gè)空的節(jié)點(diǎn)去，只會(huì)跟最后找到的葉子節(jié)點(diǎn)做融合。這個(gè)的理論指導(dǎo)，又因?yàn)榇藭r(shí) 12 是一個(gè) 2 節(jié)點(diǎn)，所以即可進(jìn)行融合，實(shí)際上它是這樣子的

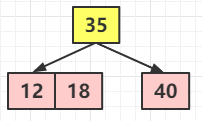
⑤ 繼續(xù)添加 10 ，10 < 35， 到左子樹(shù)查找，10 < 12 但是12 的左子樹(shù)為空，所以 10 先臨時(shí)和 12 做一個(gè)融合

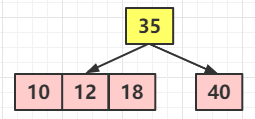
但是這個(gè)時(shí)候 12 節(jié)點(diǎn)已經(jīng)變成了 4 節(jié)點(diǎn)，所以需要拆解，理論上是這樣拆解的

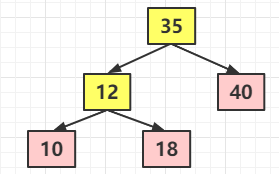
但是這樣的話 2-3 樹(shù)就不是一顆絕對(duì)平衡的樹(shù)了，顯然不能這樣拆解，或者是需要做其他操作來(lái)保持其絕對(duì)平衡。此時(shí)我們看上面的圖，12 節(jié)點(diǎn)實(shí)際上是 10 和 18 的根節(jié)點(diǎn)了，接著往上查找，12 的父節(jié)點(diǎn)是 35 而其是一個(gè) 2 節(jié)點(diǎn)，所以 12 就順理成章的和 35 融合起來(lái)，也就是下面這樣子的

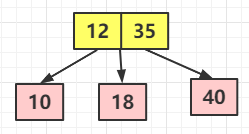
此時(shí)它又是一顆絕對(duì)平衡的 2-3 樹(shù)了

⑥ 繼續(xù)添加 11 ，那就很簡(jiǎn)單了，就不再一步一步解釋了，添加后應(yīng)該是這樣子的

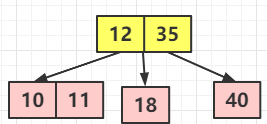
⑦ 別急，還沒(méi)完，再來(lái)一個(gè)節(jié)點(diǎn) 8，那肯定就先是這樣子的（一步一步畫(huà)其轉(zhuǎn)變的過(guò)程）

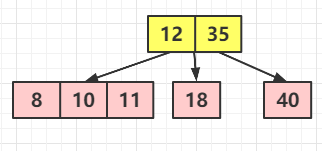
然后分裂，成這樣子

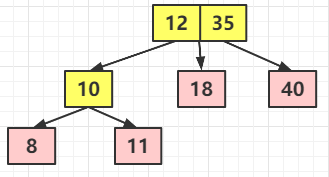
但是很顯然，此時(shí)的樹(shù)已經(jīng)失去平衡了，那就繼續(xù)轉(zhuǎn)換， 10 ?節(jié)點(diǎn)向上和根節(jié)點(diǎn)融合，但是此時(shí) 10 的父節(jié)點(diǎn)已經(jīng)是一個(gè) 3 節(jié)點(diǎn)的樹(shù)了，先融合進(jìn)去再說(shuō)

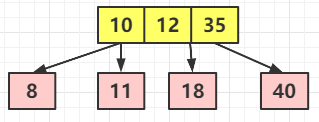
此時(shí)是 4 節(jié)點(diǎn)，已經(jīng)不是 2-3 樹(shù)了，所以下一步是這樣演變的，直接將中間的（為什么是中間的？因?yàn)檫@個(gè)依舊符合二叉搜索樹(shù)的特性，也就是左小右大）12 節(jié)點(diǎn)向上分裂，也就是最終是這樣子的

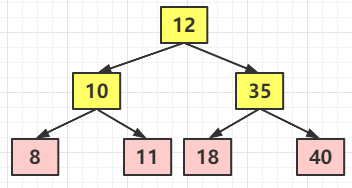
到此，我忍不住喊了一聲

2-3 樹(shù)的時(shí)間復(fù)雜度是Ologn，實(shí)際上紅黑樹(shù)就是由 2-3 樹(shù)推導(dǎo)出來(lái)的，2-3 樹(shù)和紅黑樹(shù)的關(guān)系是：2-3 樹(shù)的插入和刪除過(guò)程也可以對(duì)應(yīng)到紅黑樹(shù)的旋轉(zhuǎn)與顏色變換過(guò)程（至于紅黑樹(shù)的旋轉(zhuǎn)和變色在紅黑樹(shù)中會(huì)重點(diǎn)討論）。

那既然 2-3 樹(shù)這么厲害，干嘛還要費(fèi)那么大勁研究紅黑樹(shù)呢？那是因?yàn)閷?duì)于 2-3 樹(shù)我們需要維護(hù)兩種不同類(lèi)型的節(jié)點(diǎn)，查找和插入操作的實(shí)現(xiàn)需要大量的代碼，而且它們所產(chǎn)生的額外開(kāi)銷(xiāo)可能會(huì)使算法比標(biāo)準(zhǔn)的二叉查找樹(shù)更慢。所以這才有個(gè)紅黑樹(shù)。

6、紅黑樹(shù)

上面為什么不常見(jiàn)的 2-3 樹(shù)說(shuō)了那么多？因?yàn)?2-3樹(shù)的插入和刪除過(guò)程也可以對(duì)應(yīng)到紅黑樹(shù)的旋轉(zhuǎn)與顏色變換過(guò)程。下面我們先來(lái)了解下什么叫紅黑樹(shù)

#?紅黑樹(shù)的定義（特性）
1.?根節(jié)點(diǎn)是【黑色】
2.?每個(gè)節(jié)點(diǎn)要么是【黑色】要么是【紅色】
3.?每個(gè)【紅色】節(jié)點(diǎn)的兩個(gè)子節(jié)點(diǎn)一定都是【黑色】
4.?每個(gè)葉子節(jié)點(diǎn)（NIL）都是【黑色】
5.?任意一個(gè)節(jié)點(diǎn)的路徑到葉子節(jié)點(diǎn)所包含的【黑色】節(jié)點(diǎn)的數(shù)量是相同的---這個(gè)也稱(chēng)之為【黑色完美平衡】
6.?新插入的節(jié)點(diǎn)必須是【紅色】->為什么？如果新插入的節(jié)點(diǎn)是【黑色】，那不管是在插入到那里，一定會(huì)破壞黑色完美平衡的，因?yàn)槿我庖粋€(gè)節(jié)點(diǎn)的路徑到葉子節(jié)點(diǎn)的黑色節(jié)點(diǎn)的數(shù)量肯定不一樣了（第 6 點(diǎn)我自己加的，實(shí)際特性的定義是前 5 個(gè)）

紅黑樹(shù)的最大高度是 2logn，這看起來(lái)查找的效率并不是 AVL 樹(shù)要好，紅黑樹(shù)的的添加和刪除元素的時(shí)間復(fù)雜度是O(logn)，因?yàn)樗粫?huì)退化成想二叉搜索樹(shù)的鏈表的結(jié)構(gòu)

相信看完定義你一定一臉懵逼，別急，一步一步來(lái)，首先來(lái)畫(huà)個(gè)圖幫助大家理解

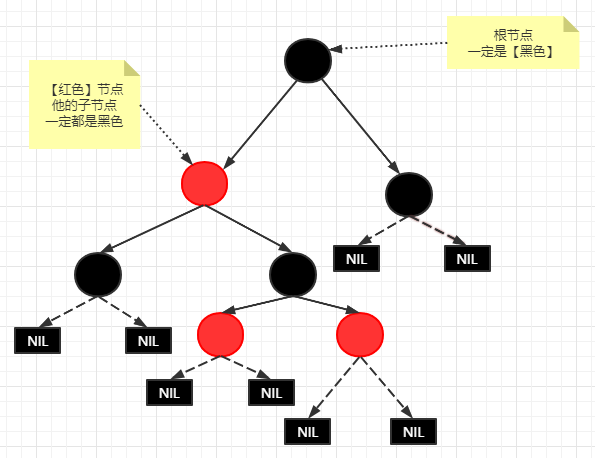
好，看到這里，小伙伴們一定是一頭霧水，光說(shuō)定義（網(wǎng)上到處都是）其實(shí)根本就無(wú)法解釋清楚叫紅黑樹(shù)。

也就是說(shuō)紅黑樹(shù)是一種平衡的檢索樹(shù)，上面的 AVL 樹(shù)我們剛剛說(shuō)了因?yàn)樾枰l繁的進(jìn)行自平衡，所以在添加和刪除節(jié)點(diǎn)的情況下性能是嚴(yán)重下降的，我們先來(lái)看下紅黑樹(shù)和 AVL 樹(shù)的比較

#?紅黑樹(shù)與AVL樹(shù)的比較
1.?AVL樹(shù)的時(shí)間復(fù)雜度優(yōu)于紅黑樹(shù)，但是對(duì)于現(xiàn)在的計(jì)算機(jī)，這種差別可以忽略
2.?紅黑樹(shù)的插入刪除比AVL樹(shù)更便于控制操作。
3.?紅黑樹(shù)整體性能略優(yōu)于AVL樹(shù)。（紅黑樹(shù)旋轉(zhuǎn)情況少于AVL樹(shù)）。這點(diǎn)是非常重要的
4.?如果是在查詢很多增刪少的情況下?AVL?樹(shù)還是優(yōu)于紅黑樹(shù)的，如果增刪比較頻繁，那紅黑樹(shù)絕對(duì)是完美的一種選擇

那紅黑樹(shù)在添加和刪除節(jié)點(diǎn)的時(shí)候是靠什么來(lái)維持平衡的呢？那就是左旋、右旋加變色

下面分別先來(lái)看下左旋、右旋加變色的定義

左旋:以某個(gè)節(jié)點(diǎn)作為固定支撐點(diǎn)（圍繞該節(jié)點(diǎn)旋轉(zhuǎn)）,其右子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的父節(jié)點(diǎn)，右子節(jié)點(diǎn)的左子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的右子節(jié)點(diǎn)，左子節(jié)點(diǎn)保持不變

右旋:?以某個(gè)節(jié)點(diǎn)作為固定支撐點(diǎn)（圍繞該節(jié)點(diǎn)旋轉(zhuǎn)），其左子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的父節(jié)點(diǎn)，左子節(jié)點(diǎn)的右子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的左子節(jié)點(diǎn)，右子節(jié)點(diǎn)保持不變
?
變色:節(jié)點(diǎn)的顏色由紅色變成黑色，或者是由黑色變成紅色

下圖分別通過(guò)畫(huà)圖來(lái)拆解各個(gè)步驟（在演示旋轉(zhuǎn)的時(shí)候我們先屏蔽掉顏色的干擾，單純來(lái)看旋轉(zhuǎn)的特性）

6.1、左旋

R 表示旋轉(zhuǎn)節(jié)點(diǎn)，沒(méi)有別的特殊的含義，以下的節(jié)點(diǎn)都是沒(méi)有任何實(shí)際意義的

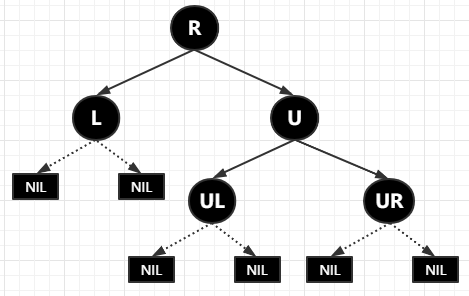
假設(shè)這是一個(gè)帶旋轉(zhuǎn)的樹(shù)，假設(shè)以 R 點(diǎn)為旋轉(zhuǎn)節(jié)點(diǎn)，根據(jù)左旋特性第一點(diǎn)：旋轉(zhuǎn)節(jié)點(diǎn)的右子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的父節(jié)點(diǎn)

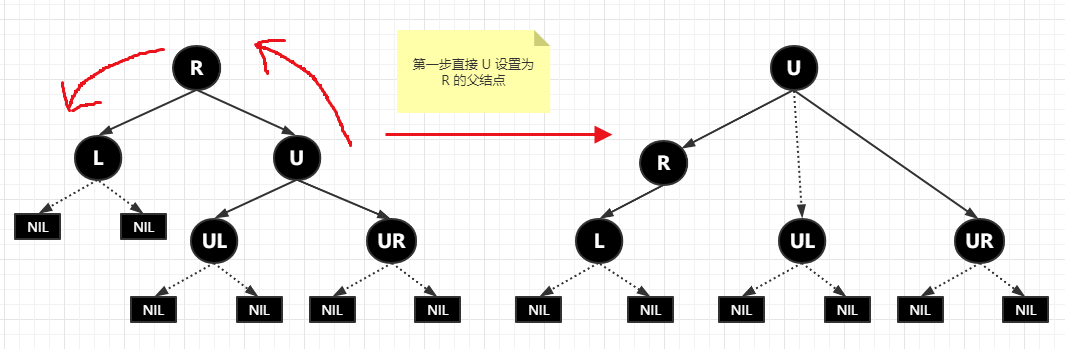
以上的圖應(yīng)該不難想象，先啥也不管，不是要左旋嗎？那就直接找到旋轉(zhuǎn)節(jié)點(diǎn)，然后將旋轉(zhuǎn)節(jié)點(diǎn)的右子節(jié)點(diǎn)設(shè)置成旋轉(zhuǎn)節(jié)點(diǎn)的父節(jié)點(diǎn)。下一步，將旋轉(zhuǎn)節(jié)點(diǎn)的右子節(jié)點(diǎn)的左子節(jié)點(diǎn)設(shè)置為旋轉(zhuǎn)節(jié)點(diǎn)的右子節(jié)點(diǎn)，再看下圖

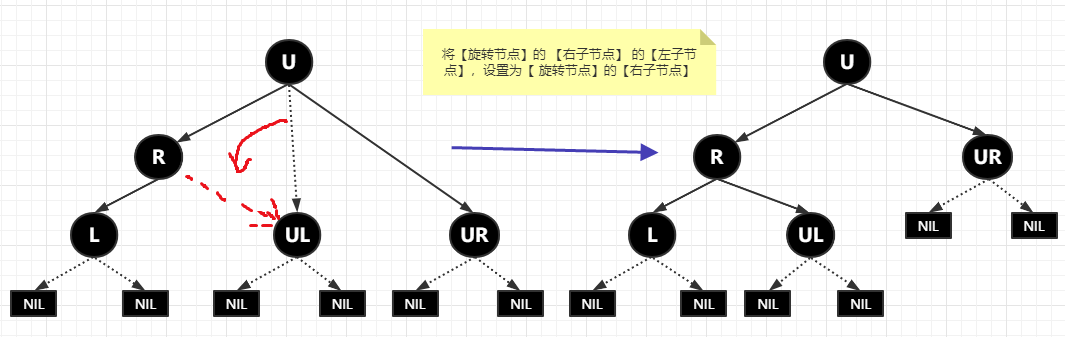
這就完事了，左旋的概念我們?cè)谝黄鸺由钕拢ㄒ驗(yàn)檫@個(gè)對(duì)于紅黑樹(shù)的平衡起到核心作用）。左旋：以某個(gè)節(jié)點(diǎn)作為固定支撐點(diǎn)（圍繞該節(jié)點(diǎn)旋轉(zhuǎn)）,其右子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的父節(jié)點(diǎn)，右子節(jié)點(diǎn)的左子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的右子節(jié)點(diǎn)，左子節(jié)點(diǎn)保持不變

6.2、右旋

右旋：以某個(gè)節(jié)點(diǎn)作為固定支撐點(diǎn)（圍繞該節(jié)點(diǎn)旋轉(zhuǎn)），其左子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的父節(jié)點(diǎn)，左子節(jié)點(diǎn)的右子節(jié)點(diǎn)變?yōu)樾D(zhuǎn)節(jié)點(diǎn)的左子節(jié)點(diǎn)，右子節(jié)點(diǎn)保持不變。還是來(lái)看圖

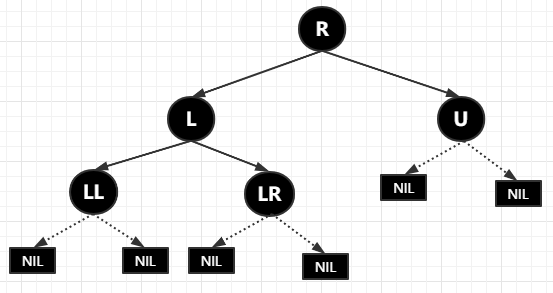
還是假設(shè)以 R 為旋轉(zhuǎn)節(jié)點(diǎn)進(jìn)行右旋，首先將 R 節(jié)點(diǎn)的左子節(jié)點(diǎn) L 設(shè)置成 R 的父節(jié)點(diǎn)，完事后是下面這樣子的

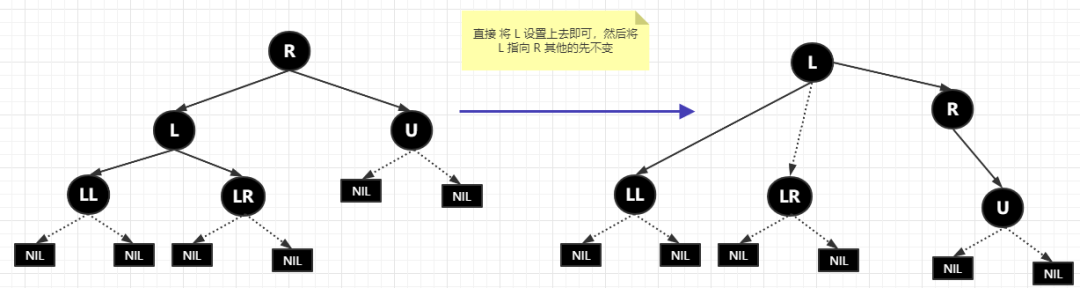
接著是第二小點(diǎn)，將 R 的左節(jié)點(diǎn)（L）的右子節(jié)點(diǎn)（LR）設(shè)置成 R 的左子節(jié)點(diǎn)，那根據(jù)上圖應(yīng)該直接就能想象出來(lái)了，那就是下面這樣子的

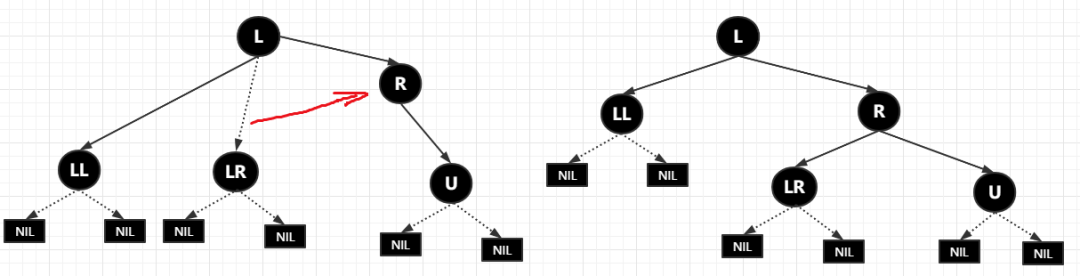
就這？還頭皮發(fā)麻不。

到此，這僅僅算是熱身吧，這是萬(wàn)里長(zhǎng)征的第一步，因?yàn)橐韵碌乃械闹v解都是在左旋右旋和變色的基礎(chǔ)上討論的（變色你不是還沒(méi)介紹嗎？黑色變紅色，紅色變黑色，介紹完了）

6.3、節(jié)點(diǎn)的查找

牢記一個(gè)原則，紅黑樹(shù)是基于二叉搜索樹(shù)的，所以查找的特性和其是類(lèi)似的，這個(gè)也不是重點(diǎn)，重點(diǎn)是紅黑樹(shù)的節(jié)點(diǎn)的添加，但是這里為啥非得提一嘴捏，因?yàn)椴迦牍?jié)點(diǎn)的時(shí)候肯定要先查找定位嘛。

6.4、節(jié)點(diǎn)的添加

先回顧下紅黑樹(shù)的性質(zhì)，為了不讓各位來(lái)回翻頁(yè)，小弟直接將其復(fù)制過(guò)來(lái)

#?紅黑樹(shù)的定義（特性）
1.?根節(jié)點(diǎn)是【黑色】
2.?每個(gè)節(jié)點(diǎn)要么是【黑色】要么是【紅色】
3.?每個(gè)【紅色】節(jié)點(diǎn)的兩個(gè)子節(jié)點(diǎn)一定都是【黑色】
4.?每個(gè)葉子節(jié)點(diǎn)（NIL）都是【黑色】
5.?任意一個(gè)節(jié)點(diǎn)的路徑到葉子節(jié)點(diǎn)所包含的【黑色】節(jié)點(diǎn)的數(shù)量是相同的---這個(gè)也稱(chēng)之為【黑色完美平衡】
6.?新插入的節(jié)點(diǎn)必須是【紅色】->為什么？如果新插入的節(jié)點(diǎn)是【黑色】，那不管是在插入到那里，一定會(huì)破壞黑色完美平衡的，因?yàn)槿我庖粋€(gè)節(jié)點(diǎn)的路徑到葉子節(jié)點(diǎn)的黑色節(jié)點(diǎn)的數(shù)量肯定不一樣了（第 6 點(diǎn)我自己加的，實(shí)際特性的定義是前 5 個(gè)）

添加實(shí)際上順帶了查找，所以在添加節(jié)點(diǎn)之前，必然要進(jìn)行查找節(jié)點(diǎn)的位置，然后再插入節(jié)點(diǎn)，最后再自平衡。其中注意上面我自己添加的第 6 點(diǎn)，那就是新插入的節(jié)點(diǎn)一定是紅色的（上面的第 6 點(diǎn)已經(jīng)說(shuō)的很清楚了，主要是為了防止一插入節(jié)點(diǎn)就破壞黑色完美平衡），不管后面怎么處理，新插入的節(jié)點(diǎn)只能是紅色節(jié)點(diǎn)。

另外，我們還需要做如下的約定，假設(shè)新添加的節(jié)點(diǎn)為 I，I 的父節(jié)點(diǎn)為 P ，P 的兄弟節(jié)點(diǎn)為 U，P 父親節(jié)點(diǎn)為（也就是 I 節(jié)點(diǎn)的爺爺節(jié)點(diǎn)） G，那這個(gè)結(jié)構(gòu)是這樣子的 （下圖不要管字母的順序，僅僅是表示一個(gè)節(jié)點(diǎn)的關(guān)系）

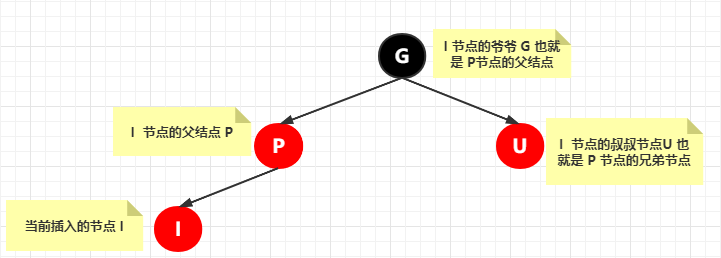
接下來(lái)是最難堅(jiān)持的各種自平衡常見(jiàn)的分析了

下面開(kāi)始進(jìn)行各種情況的分析

• 第 1 種情況：紅黑樹(shù)為空樹(shù)

那這還不好辦嘛，插入的節(jié)點(diǎn) I 就是根節(jié)點(diǎn)如下圖：

咦？插入節(jié)點(diǎn)是紅色節(jié)點(diǎn)沒(méi)毛病，但是這個(gè)也是根節(jié)點(diǎn)啊？那就變色唄，所以當(dāng)紅黑樹(shù)為空的時(shí)候新插入的節(jié)點(diǎn)直接變色即可。so easy~

• 第 2 種情況：插入的節(jié)點(diǎn)已經(jīng)存在

還是畫(huà)圖來(lái)說(shuō)，這樣更直觀

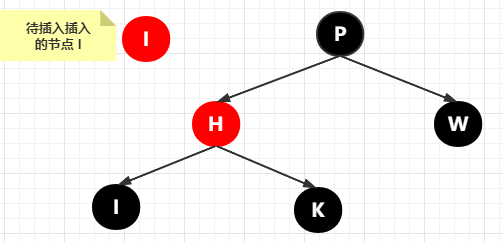
然后替換已有的 I 節(jié)點(diǎn)，如下圖

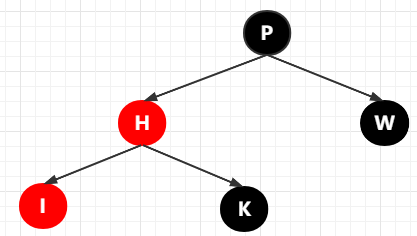
此時(shí)很顯然已經(jīng)破壞了黑色完美平衡了，這個(gè)也好說(shuō)，直接將 I 變色即可。第二種情況也不過(guò)如此嘛。

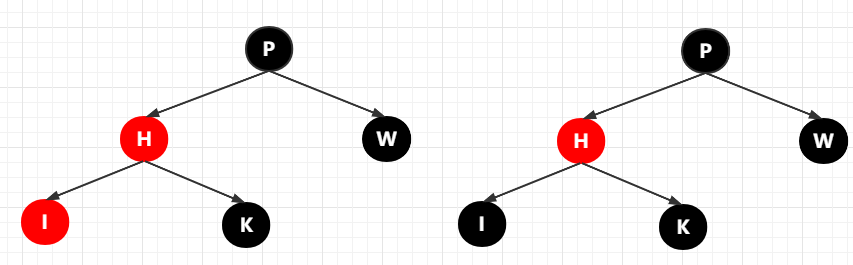
• 第 3 種情況：插入節(jié)點(diǎn)的父節(jié)點(diǎn)為黑色

假設(shè)待插入的節(jié)點(diǎn)為 Q ，那實(shí)際上應(yīng)該是這樣子的

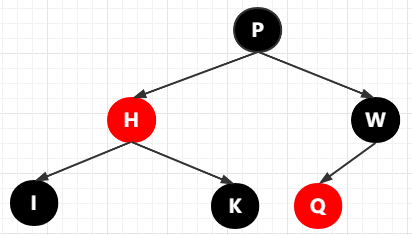
完事了，為啥？因?yàn)檫@個(gè)樹(shù)本來(lái)就是黑色完美平衡了，再新插入一個(gè)新的節(jié)點(diǎn)紅色節(jié)點(diǎn)，并不會(huì)破壞樹(shù)的平衡以及紅黑樹(shù)的特性（不要去研究為什么。科學(xué)家研究了好幾年的東西，咱就不要再去深挖了）

• 第 4 種情況：插入節(jié)點(diǎn)的父節(jié)點(diǎn)為紅色

萬(wàn)變不離其宗，繼續(xù)回顧紅黑樹(shù)性質(zhì)，插入的節(jié)點(diǎn)為紅色，根節(jié)點(diǎn)為黑色，那既然插入的節(jié)點(diǎn)的父節(jié)點(diǎn)為紅色節(jié)點(diǎn)，而紅色節(jié)點(diǎn)一定不可能為根節(jié)點(diǎn)，所以可以推斷出新插入節(jié)點(diǎn)的父節(jié)點(diǎn)一定還有父節(jié)點(diǎn)，也就是新插入的節(jié)點(diǎn)一定有爺爺節(jié)點(diǎn)。這里為什么這么強(qiáng)調(diào)，因?yàn)橐院蟮钠胶饪赡軙?huì)涉及到類(lèi)似的遞歸的自旋，直到平衡。類(lèi)似這樣子（不要關(guān)心字母的順序，僅僅表示一個(gè)關(guān)系）

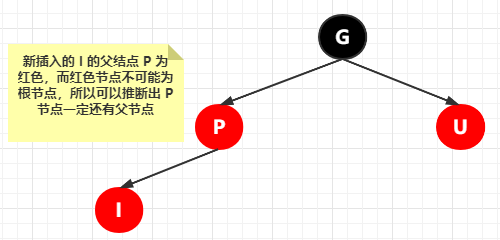
那現(xiàn)在很顯然違反了上面的特性 3 ?每個(gè)【紅色】節(jié)點(diǎn)的兩個(gè)子節(jié)點(diǎn)一定都是【黑色】,而現(xiàn)在是兩個(gè)紅色節(jié)點(diǎn)相連了，這個(gè)該怎么處理？此時(shí)又繼續(xù)拆分不同的情況了

• 第 4-1 種情況：插入節(jié)點(diǎn)的叔叔節(jié)點(diǎn)存在，且為紅色

此時(shí)又可以推斷出來(lái)叔叔節(jié)點(diǎn)的父節(jié)點(diǎn)一定是黑色，因?yàn)椴荒苡袃蓚€(gè)紅色節(jié)點(diǎn)相連（該特性和每個(gè)【紅色】節(jié)點(diǎn)的兩個(gè)子節(jié)點(diǎn)一定都是【黑色】是一個(gè)意思 ），所以這個(gè)時(shí)候你看的樹(shù)大致是這樣子的結(jié)構(gòu)

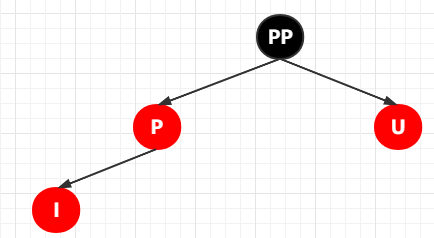
以下的處理方式是固定的。只要是這種場(chǎng)景（我們以插入節(jié)點(diǎn)和插入節(jié)點(diǎn)的父節(jié)點(diǎn)以及插入節(jié)點(diǎn)的爺爺節(jié)點(diǎn)作為一個(gè)自旋整體），那么就按照這么處理：

① 將 P 和 U 變成黑色；② 將 PP 變成 紅色。如下圖：

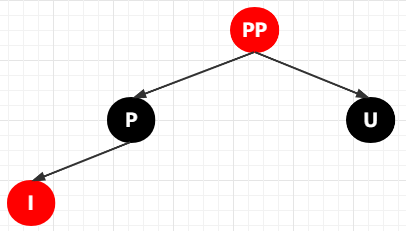
那既然 PP 是根節(jié)點(diǎn)，那肯定不可能為紅色了，接下來(lái)就是將 PP 當(dāng)作是當(dāng)前節(jié)點(diǎn)，然后繼續(xù)判斷處理。

先記住這個(gè)步驟，下面還會(huì)再說(shuō)到，因?yàn)檫@個(gè)就是紅色樹(shù)的特性，既然性質(zhì)都限制死了，那其實(shí)處理的方式也就那么幾種。我們繼續(xù)往下看

• 第 4-2 種情況：叔叔節(jié)點(diǎn)不存在或者為黑色，且插入節(jié)點(diǎn)的【父節(jié)點(diǎn)】是插入節(jié)點(diǎn)爺爺節(jié)點(diǎn)的【左子節(jié)點(diǎn)】

說(shuō)了再多不如一張圖搞定（不要忘記第四種情況的大前提，插入節(jié)點(diǎn)的父節(jié)點(diǎn)為紅色）

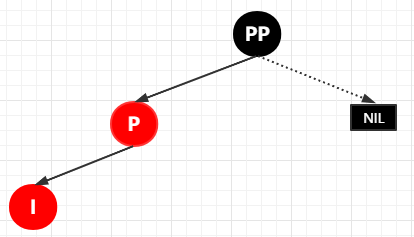
實(shí)際上上圖是稍微有點(diǎn)不合理的，因?yàn)檫@樣子的話就破壞了黑色完美平衡了，也就是說(shuō)叔叔節(jié)點(diǎn)如果不是紅色，那肯定也不可能是黑色的，那剩下的只能是 NULL，下面這張圖才是比較合適的表達(dá) 4-2 的情況。

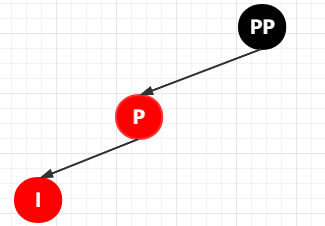
等等，為啥說(shuō)是比較合適的？因?yàn)椴迦氲墓?jié)點(diǎn)可能為其父節(jié)點(diǎn)的左子節(jié)點(diǎn)，也可能是其父節(jié)點(diǎn)的右子節(jié)點(diǎn)。下面這樣圖才是完美的

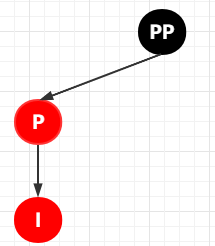
那既然不確定是左子節(jié)點(diǎn)還是右子節(jié)點(diǎn)，那肯定是要繼續(xù)分情況了唄，沒(méi)錯(cuò)

• 第 4-2-1 種情況：插入節(jié)點(diǎn)為其父節(jié)點(diǎn)的左子節(jié)點(diǎn)，也即 LL 雙紅色的情況（第一個(gè) L 表示插入節(jié)點(diǎn)的父節(jié)點(diǎn)，第二個(gè) L 表示插入節(jié)點(diǎn)）

那這種情況肯定就是這樣子的了

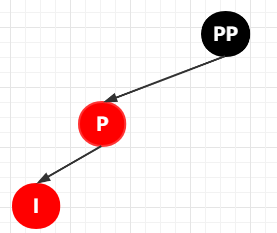
這個(gè)怎么搞了？我說(shuō)接下來(lái)更簡(jiǎn)單你可能會(huì)不信，其實(shí)就像我剛剛上面說(shuō)的，步驟都是固定的，接下來(lái)為了平衡，步驟為：

① 將 P 節(jié)點(diǎn)變成黑色，將 PP 節(jié)點(diǎn)變成 紅色

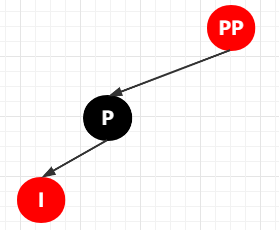
② 對(duì) PP 節(jié)點(diǎn)進(jìn)行右旋（以 PP 節(jié)點(diǎn)為旋轉(zhuǎn)節(jié)點(diǎn)，進(jìn)行右旋）

右旋的特點(diǎn)還記得不？右旋：旋轉(zhuǎn)節(jié)點(diǎn)的左子節(jié)點(diǎn)變成其父節(jié)點(diǎn)，旋轉(zhuǎn)節(jié)點(diǎn)的左子節(jié)點(diǎn)的右子節(jié)點(diǎn)變成旋轉(zhuǎn)節(jié)點(diǎn)的左子節(jié)點(diǎn)，那這個(gè)旋轉(zhuǎn)節(jié)點(diǎn)的左子節(jié)點(diǎn)的右子節(jié)點(diǎn)不是為 NULL 嘛？那就不管唄，所以，以 PP 為旋轉(zhuǎn)節(jié)點(diǎn)的旋轉(zhuǎn)后的結(jié)果是：

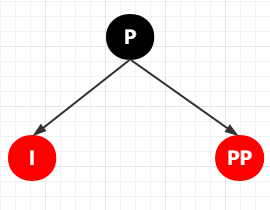
其完整的變換流程如下：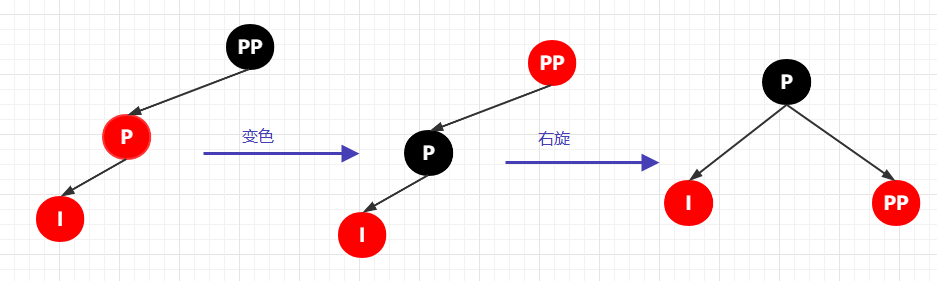

• 第 4-2-2 種情況：插入節(jié)點(diǎn)為其父節(jié)點(diǎn)的右子節(jié)點(diǎn)，也即 LR 雙紅色的情況

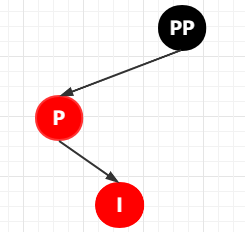
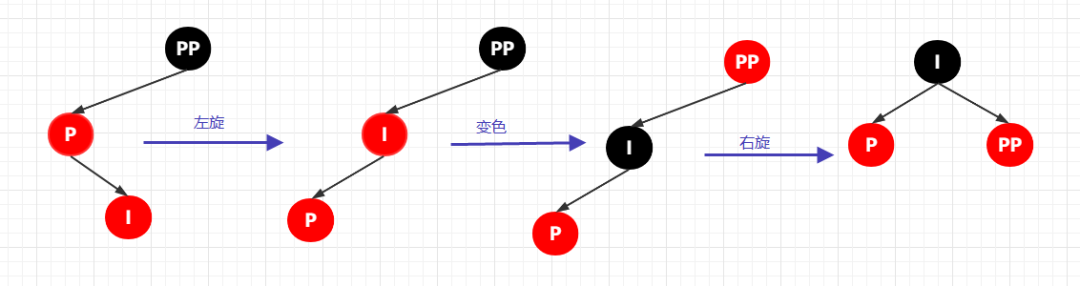
這個(gè)時(shí)候處理方式依舊是固定的，就是將其變成 LL 雙紅的情況，然后按照 LL 雙紅的情況去處理。那么問(wèn)題來(lái)了，該如何才能變成 LL 雙紅的情況呢？依舊是固定的套路，直接按照以下的步驟操作：

① 將 P 節(jié)點(diǎn)作為旋轉(zhuǎn)節(jié)點(diǎn)，進(jìn)行左旋，其結(jié)果是這樣子的

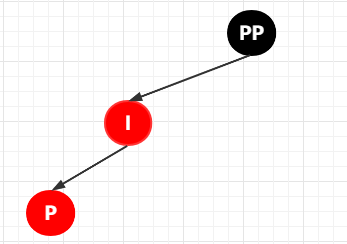
② 這個(gè)時(shí)候就變成了了熟悉的味道了，接下來(lái)就按照 LL 雙紅的情況來(lái)處理：① 將 I 變成黑色，將 PP 變成紅色，② 然后以 PP 為旋轉(zhuǎn)節(jié)點(diǎn)，進(jìn)行右旋

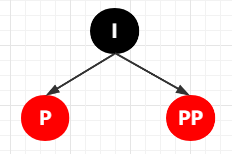
其完成的變換流程如下：

• 第 4-3 種情況：叔叔節(jié)點(diǎn)不存在或者為黑色，且插入節(jié)點(diǎn)的【父節(jié)點(diǎn)】是插入節(jié)點(diǎn)爺爺節(jié)點(diǎn)的【右子節(jié)點(diǎn)】

4-3 這種情況和 4-2 剛好反過(guò)來(lái)，但是我還是會(huì)一步一步來(lái)介紹的

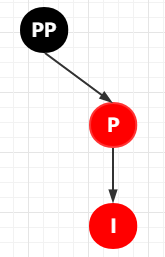
這種情況依舊是繼續(xù)區(qū)分插入節(jié)點(diǎn)是其父節(jié)點(diǎn)的左子節(jié)點(diǎn)還是右子節(jié)點(diǎn)

• 第 4-3-1 種情況：插入節(jié)點(diǎn)為其父節(jié)點(diǎn)的右子節(jié)點(diǎn)，也即 RR 雙紅色的情況（第一個(gè) R 是插入節(jié)點(diǎn)的父節(jié)點(diǎn)，第二個(gè) R 是插入節(jié)點(diǎn)）

也就是下面這樣子的

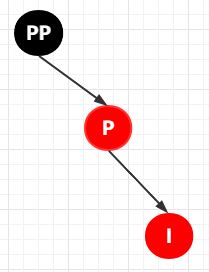
處理步驟如下：

① 將 P 設(shè)置為 黑色，將 PP 設(shè)置為紅色

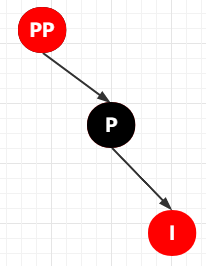
② 以 PP 節(jié)點(diǎn)為旋轉(zhuǎn)節(jié)點(diǎn)，進(jìn)行左旋

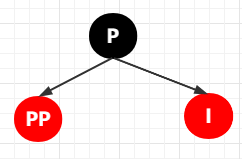
其整個(gè)轉(zhuǎn)換流程是這樣的

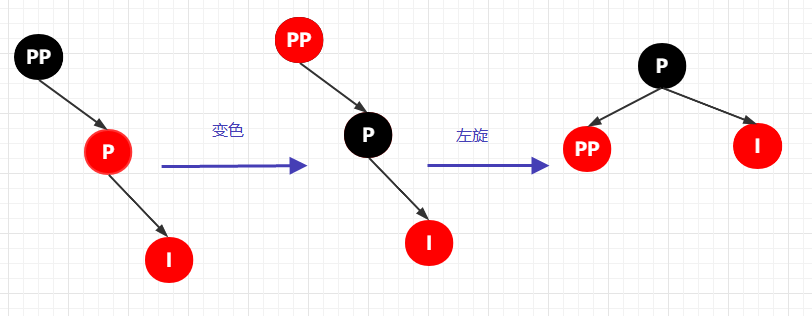
• 第 4-3-2 種情況：插入節(jié)點(diǎn)為其父節(jié)點(diǎn)的左子節(jié)點(diǎn)，也即 RL 雙紅色的情況

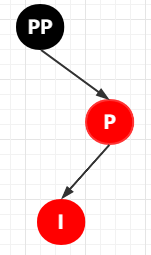
你是不是覺(jué)得對(duì)于這種情況那不就是應(yīng)該先將 RL 轉(zhuǎn)換成 RR 這種情況嗎？沒(méi)錯(cuò)，就是這樣，我發(fā)現(xiàn)你都開(kāi)始學(xué)會(huì)搶答了。

這個(gè)時(shí)候處理的步驟是這樣子的：首先以 P 節(jié)點(diǎn)為旋轉(zhuǎn)節(jié)點(diǎn)，進(jìn)行右旋，結(jié)果是這樣子的

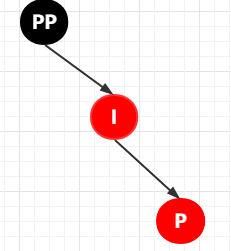
然后將 I 設(shè)置為 黑色，將 PP 設(shè)置為紅色

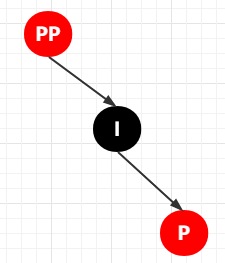
然后以 PP 為旋轉(zhuǎn)節(jié)點(diǎn)，進(jìn)行左旋

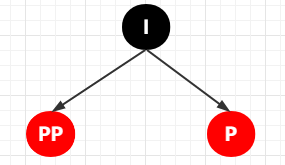
其完整的轉(zhuǎn)換流程是這樣子的：

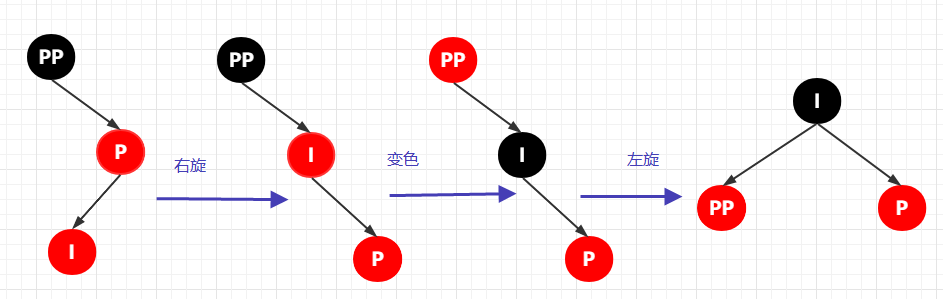
好了，我們趕緊做個(gè)總結(jié)，相信很多小伙伴看了上面的各種情況基本已經(jīng)凌亂了，甚至都沒(méi)看到這里就撤了。。下面我們將各個(gè)情況總結(jié)如下

6.5、結(jié)束語(yǔ)

最后我們?cè)賮?lái)對(duì)紅黑樹(shù)自平衡的各個(gè)情況做個(gè)總結(jié)：

紅黑樹(shù)性質(zhì)：
????根節(jié)點(diǎn)為黑色
????節(jié)點(diǎn)不是紅色就是黑色
????每個(gè)葉子節(jié)點(diǎn)NIL為黑色
????紅色節(jié)點(diǎn)的兩個(gè)子節(jié)點(diǎn)一定都是黑色
????任意一個(gè)節(jié)點(diǎn)到葉子節(jié)點(diǎn)的路徑都包含相同數(shù)量的黑色節(jié)點(diǎn)，俗稱(chēng)：黑高
????（如果一個(gè)節(jié)點(diǎn)的存在黑子節(jié)點(diǎn)，那么該節(jié)點(diǎn)肯定有兩個(gè)子節(jié)點(diǎn)）

當(dāng)前節(jié)點(diǎn)為I，父節(jié)點(diǎn)為P，P節(jié)點(diǎn)的兄弟節(jié)點(diǎn)為U，P的父節(jié)點(diǎn)為PP（祖父節(jié)點(diǎn)）
1、當(dāng)前節(jié)點(diǎn)為空，直接插入即可
2、插入的節(jié)點(diǎn)已經(jīng)存在，直接替換即可
3、插入節(jié)點(diǎn)的父節(jié)點(diǎn)為【黑色節(jié)點(diǎn)】，找到父節(jié)點(diǎn)，直接插入即可。不會(huì)影響完美黑平衡
4、插入節(jié)點(diǎn)的父節(jié)點(diǎn)為【紅色節(jié)點(diǎn)】
??? 4.1、叔叔節(jié)點(diǎn)存在，且為【紅色節(jié)點(diǎn)】
????由紅黑樹(shù)的性質(zhì)可知：紅色節(jié)點(diǎn)不能相連，=》祖父節(jié)點(diǎn)肯定為黑色節(jié)點(diǎn)
????此時(shí)紅黑層數(shù)情況是【黑紅紅】，最簡(jiǎn)單的處理方式就是改成【紅黑紅】
????處理方式：
????????將P和U改為黑色
????????PP改為紅色
????????將PP節(jié)點(diǎn)設(shè)置為當(dāng)前節(jié)點(diǎn)，進(jìn)行后續(xù)處理
????4.2、叔叔節(jié)點(diǎn)不存在或者叔叔節(jié)點(diǎn)是【黑色節(jié)點(diǎn)】且插入節(jié)點(diǎn)的父節(jié)點(diǎn)是祖父節(jié)點(diǎn)的左子節(jié)點(diǎn)
??????? 4.2.1、插入節(jié)點(diǎn)為其父節(jié)點(diǎn)的左子節(jié)點(diǎn)（這個(gè)時(shí)候是LL雙紅的情況：當(dāng)前節(jié)點(diǎn)為紅色，當(dāng)前節(jié)點(diǎn)的父節(jié)點(diǎn)為紅色，當(dāng)前節(jié)點(diǎn)為其父節(jié)點(diǎn)的左子節(jié)點(diǎn)）
????????處理方式：
????????????????變顏色：將P節(jié)點(diǎn)設(shè)置為黑色，將PP節(jié)點(diǎn)設(shè)置為紅色
????????????????對(duì)PP節(jié)點(diǎn)進(jìn)行右旋
??????? 4.2.2、插入節(jié)點(diǎn)為其父節(jié)點(diǎn)的右子節(jié)點(diǎn)（這個(gè)時(shí)候是LR雙紅的情況：當(dāng)前節(jié)點(diǎn)為紅色，當(dāng)前節(jié)點(diǎn)的父節(jié)點(diǎn)為紅色，當(dāng)前節(jié)點(diǎn)為其父節(jié)點(diǎn)的右子節(jié)點(diǎn)）
????????處理方式：
????????????對(duì)P節(jié)點(diǎn)進(jìn)行左旋，這個(gè)時(shí)候就會(huì)變成LL雙紅
????????????此時(shí)按照4.2.1的處理方式處理
????4.3、叔叔節(jié)點(diǎn)不存在或者叔叔節(jié)點(diǎn)是【黑色節(jié)點(diǎn)】且插入節(jié)點(diǎn)的父節(jié)點(diǎn)為祖父節(jié)點(diǎn)的右子節(jié)點(diǎn)
??????? 4.3.1、插入節(jié)點(diǎn)為其父節(jié)點(diǎn)的右子節(jié)點(diǎn)（這個(gè)時(shí)候是RR雙紅的情況：當(dāng)前節(jié)點(diǎn)為紅色，當(dāng)前節(jié)點(diǎn)的父節(jié)點(diǎn)為紅色，當(dāng)前節(jié)點(diǎn)為其父節(jié)點(diǎn)的右子節(jié)點(diǎn)）
????????處理方式：
????????????變顏色：將P節(jié)點(diǎn)設(shè)置為黑色，將PP節(jié)點(diǎn)設(shè)置為紅色
????????????對(duì)PP節(jié)點(diǎn)進(jìn)行左旋
??????? 4.3.2、插入節(jié)點(diǎn)為其父節(jié)點(diǎn)的左子節(jié)點(diǎn)（這個(gè)時(shí)候是RL雙紅的情況：當(dāng)前節(jié)點(diǎn)為紅色，當(dāng)前節(jié)點(diǎn)的父節(jié)點(diǎn)為紅色，當(dāng)前節(jié)點(diǎn)為其父節(jié)點(diǎn)的左子節(jié)點(diǎn)）
????????處理方式：
????????????對(duì)P節(jié)點(diǎn)進(jìn)行右旋，這個(gè)時(shí)候變成RR雙紅
????????????此時(shí)按照4.3.1的方式進(jìn)行處理