无码成人一区二区三区四区五区,一区在线观看视频,色福利视频,影音先锋资源你懂的,中文字幕www,五月天欧美性爱,夏晴子在线观看,蜜桃亚洲AV啪啪无码片

動態(tài)規(guī)劃是一個從其他行業(yè)借鑒過來的詞語。

它的大概意思先將一件事情分成「若干階段」，然后通過階段之間的「轉(zhuǎn)移」達到目標。由于轉(zhuǎn)移的方向通常是多個，因此這個時候就需要「決策」選擇具體哪一個轉(zhuǎn)移方向。

動態(tài)規(guī)劃所要解決的事情通常是完成一個具體的目標，而這個目標往往是最優(yōu)解。并且：

階段之間可以進行轉(zhuǎn)移，這叫做動態(tài)。
達到一個「可行解(目標階段)」 需要不斷地轉(zhuǎn)移，那如何轉(zhuǎn)移才能達到「最優(yōu)解」？這叫規(guī)劃。

每個階段抽象為狀態(tài)（用圓圈來表示），狀態(tài)之間可能會發(fā)生轉(zhuǎn)化（用箭頭表示）。可以畫出類似如下的圖：

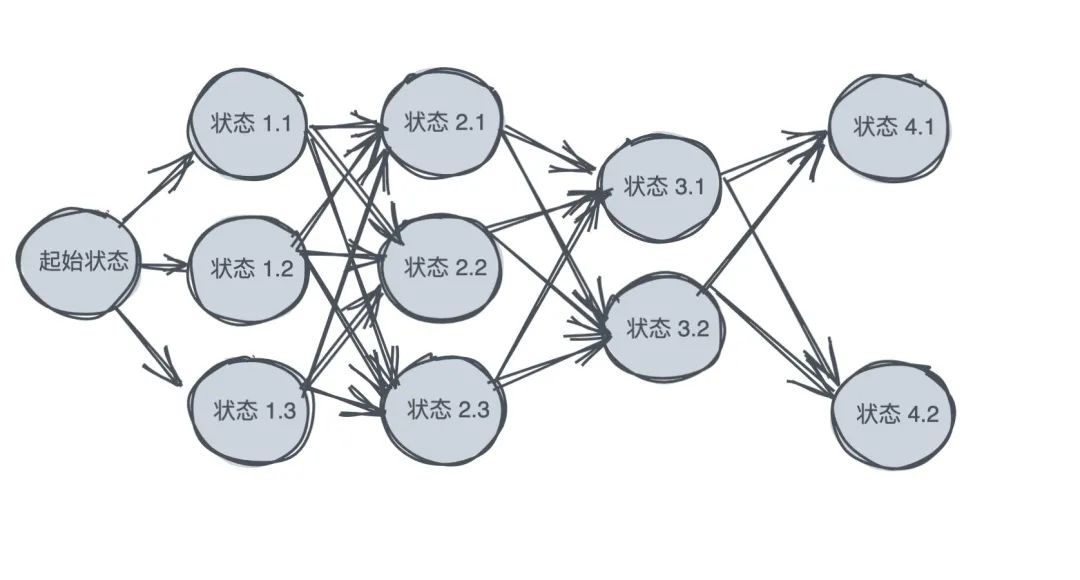
那我們應該做出如何的「決策序列」才能使得結(jié)果最優(yōu)？換句話說就是每一個狀態(tài)應該如何選擇到下一個具體狀態(tài)，并最終到達目標狀態(tài)。這就是動態(tài)規(guī)劃研究的問題。

每次決策實際上「不會考慮之后的決策，而只會考慮之前的狀態(tài)。」 形象點來說，其實是走一步看一步這種短視思維。為什么這種短視可以來求解最優(yōu)解呢？那是因為：

我們將「所有可能的轉(zhuǎn)移全部模擬了一遍」，最后挑了一個最優(yōu)解。
無后向性（這個我們后面再說，先賣個關子）

?
而如果你沒有模擬所有可能，而直接走了一條最優(yōu)解，那就是貪心算法了。
?

沒錯，動態(tài)規(guī)劃剛開始就是來求最優(yōu)解的。只不過有的時候順便可以求總的方案數(shù)等其他東西，這其實是「動態(tài)規(guī)劃的副產(chǎn)物」。

好了，我們把動態(tài)規(guī)劃拆成兩部分分別進行解釋，或許你大概知道了動態(tài)規(guī)劃是一個什么樣的東西。但是這對你做題并沒有幫助。那算法上的動態(tài)規(guī)劃究竟是個啥呢？

在算法上，動態(tài)規(guī)劃和「查表的遞歸（也稱記憶化遞歸）」 有很多相似的地方。我建議大家先從記憶化遞歸開始學習。本文也先從記憶化遞歸開始，逐步講解到動態(tài)規(guī)劃。

記憶化遞歸

那么什么是遞歸？什么是查表（記憶化）？讓我們慢慢來看。

什么是遞歸？

遞歸是指在函數(shù)中「調(diào)用函數(shù)自身」的方法。

有意義的遞歸通常會把問題分解成「規(guī)模縮小的同類子問題」，當子問題縮寫到尋常的時候，我們可以直接知道它的解。然后通過建立遞歸函數(shù)之間的聯(lián)系（轉(zhuǎn)移）即可解決原問題。

?
是不是和分治有點像? 分治指的是將問題一分為多，然后將多個解合并為一。而這里并不是這個意思。
?

一個問題要使用遞歸來解決必須有遞歸終止條件（算法的有窮性），也就是說遞歸會逐步縮小規(guī)模到尋常。

雖然以下代碼也是遞歸，但由于其無法結(jié)束，因此不是一個有效的算法：

def?f(x):
??return?x?+?f(x?-?1)

上面的代碼除非外界干預，否則會永遠執(zhí)行下去，不會停止。

因此更多的情況應該是：

def?f(n):
??if?n?==?1:?return?1
??return?n?+?f(n?-?1)

使用遞歸通常可以使代碼短小，有時候也更可讀。算法中使用遞歸可以「很簡單地」完成一些用循環(huán)不太容易實現(xiàn)的功能，比如二叉樹的左中右序遍歷。

遞歸在算法中有非常廣泛的使用，包括現(xiàn)在日趨流行的函數(shù)式編程。

?
遞歸在函數(shù)式編程中地位很高。純粹的函數(shù)式編程中沒有循環(huán)，只有遞歸。
?

實際上，除了在編碼上通過函數(shù)調(diào)用自身實現(xiàn)遞歸。我們也可以定義遞歸的數(shù)據(jù)結(jié)構。比如大家所熟知的樹，鏈表等都是遞歸的數(shù)據(jù)結(jié)構。

Node?{
?value:?any;?//?當前節(jié)點的值
?children:?Array;?//?指向其兒子
}

如上代碼就是一個多叉樹的定義形式，可以看出 children 就是 Node 的集合類，這就是一種「遞歸的數(shù)據(jù)結(jié)構」。

不僅僅是普通的遞歸函數(shù)

本文中所提到的記憶化遞歸中的遞歸函數(shù)實際上「指的是特殊的遞歸函數(shù)」，即在普通的遞歸函數(shù)上滿足以下幾個條件：

遞歸函數(shù)不依賴外部變量
遞歸函數(shù)不改變外部變量

?
滿足這兩個條件有什么用呢？這是因為我們需要函數(shù)給定參數(shù)，其返回值也是確定的。這樣我們才能記憶化。關于記憶化，我們后面再講。
?

如果大家了解函數(shù)式編程，實際上這里的遞歸其實嚴格來說是「函數(shù)式編程中的函數(shù)」。如果不了解也沒關系，這里的遞歸函數(shù)其實就是「數(shù)學中的函數(shù)」。

我們來回顧一下數(shù)學中的函數(shù)：

在一個變化過程中，假設有兩個變量 x、y，如果對于任意一個 x 都有唯一確定的一個 y 和它對應，那么就稱 x 是自變量，y 是 x 的函數(shù)。x 的取值范圍叫做這個函數(shù)的定義域，相應 y 的取值范圍叫做函數(shù)的值域?。

而「本文所講的所有遞歸都是指的這種數(shù)學中的函數(shù)。」

比如上面的遞歸函數(shù)：

def?f(x):
??if?x?==?1:?return?1
??return?x?+?f(x?-?1)

x 就是自變量，x 的所有可能的返回值構成的集合就是定義域。
f(x) 就是函數(shù)。
f(x) 的所有可能的返回值構成的集合就是值域。

自變量也可以有多個，對應遞歸函數(shù)的參數(shù)可以有多個，比如 f(x1, x2, x3)。

「通過函數(shù)來描述問題，并通過函數(shù)的調(diào)用關系來描述問題間的關系就是記憶化遞歸的核心內(nèi)容。」

每一個動態(tài)規(guī)劃問題，實際上都可以抽象為一個數(shù)學上的函數(shù)。這個函數(shù)的自變量集合就是題目的所有取值，值域就是題目要求的答案的所有可能。我們的目標其實就是填充這個函數(shù)的內(nèi)容，使得給定自變量 x，能夠唯一映射到一個值 y。（當然自變量可能有多個，對應遞歸函數(shù)參數(shù)可能有多個）

解決動態(tài)規(guī)劃問題可以看成是填充函數(shù)這個黑盒，使得定義域中的數(shù)并正確地映射到值域。

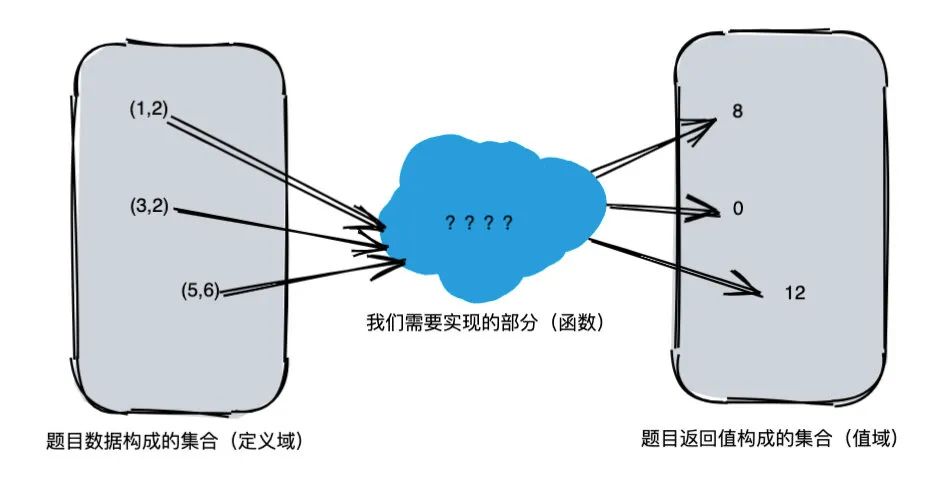
遞歸并不是算法，它是和迭代對應的一種編程方法。只不過，我們通常借助遞歸去分解問題而已。比如我們定義一個遞歸函數(shù) f(n)，用 f(n) 來描述問題。就和使用普通動態(tài)規(guī)劃 f[n] 描述問題是一樣的，這里的 f 是 dp 數(shù)組。

什么是記憶化？

為了大家能夠更好地對本節(jié)內(nèi)容進行理解，我們通過一個例子來切入：

一個人爬樓梯，每次只能爬 1 個或 2 個臺階，假設有 n 個臺階，那么這個人有多少種不同的爬樓梯方法？

思路：

由于「第 n 級臺階一定是從 n - 1 級臺階或者 n - 2 級臺階來的」，因此到第 n 級臺階的數(shù)目就是 到第 n - 1 級臺階的數(shù)目加上到第 n - 1 級臺階的數(shù)目。

遞歸代碼：

function?climbStairs(n)?{
??if?(n?===?1)?return?1;
??if?(n?===?2)?return?2;
??return?climbStairs(n?-?1)?+?climbStairs(n?-?2);
}

我們用一個遞歸樹來直觀感受以下（每一個圓圈表示一個子問題）：

紅色表示重復的計算。即 Fib(N-2) 和 Fib(N-3) 都被計算了兩次，實際上計算一次就夠了。比如第一次計算出了 Fib(N-2) 的值，那么下次再次需要計算 Fib(N-2)的時候，可以直接將上次計算的結(jié)果返回。之所以可以這么做的原因正是前文提到的「我們的遞歸函數(shù)是數(shù)學中的函數(shù)，也就是說參數(shù)一定，那么返回值也一定不會變」，因此下次如果碰到相同的參數(shù)，我們就可以「將上次計算過的值直接返回，而不必重新計算」。這樣節(jié)省的時間就等價于重疊子問題的個數(shù)。

「以這道題來說，本來需要計算次，而如果使用了記憶化，只需要計算 n 次，就是這么神奇。」

代碼上，我們可以使用一個 hashtable 去緩存中間計算結(jié)果，從而省去不必要的計算。

我們使用記憶化來改造上面的代碼：

memo?=?{}
def?climbStairs(n):
??if?n?==?1:return?1
??if?n?==?2:?return?2
??if?n?in?memo:?return?memo[n]
??ans?=?func(n?-?1)?+?func(n-2)
??memo[n]?=?ans
??return?ans
climbStairs(10)

這里我使用了一個名為 「memo 的哈希表來存儲遞歸函數(shù)的返回值，其中 key 為參數(shù)，value 為遞歸函數(shù)的返回值。」

?
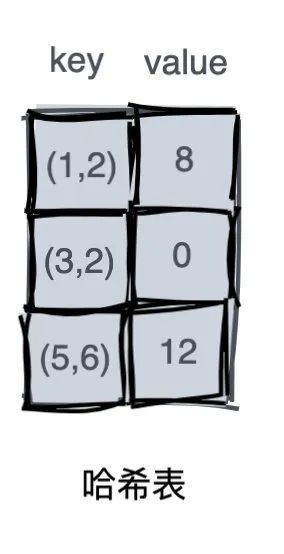
key 的形式為 (x, y)，表示的是一個元祖。通常動態(tài)規(guī)劃的參數(shù)有多個，我們就可以使用元祖的方式來記憶化。或者也可采取多維數(shù)組的形式。對于上圖來說，就可使用二維數(shù)組來表示。
?

大家可以通過刪除和添加代碼中的 memo 來感受一下「記憶化」的作用。

小結(jié)

使用遞歸函數(shù)的優(yōu)點是邏輯簡單清晰，缺點是過深的調(diào)用會導致棧溢出。這里我列舉了幾道算法題目，這幾道算法題目都可以用遞歸輕松寫出來：

遞歸實現(xiàn) sum
二叉樹的遍歷
走樓梯問題
漢諾塔問題
楊輝三角

遞歸中「如果」存在重復計算（我們稱重疊子問題，下文會講到），那就是使用記憶化遞歸（或動態(tài)規(guī)劃）解題的強有力信號之一。可以看出動態(tài)規(guī)劃的核心就是使用記憶化的手段消除重復子問題的計算，如果這種重復子問題的規(guī)模是指數(shù)或者更高規(guī)模，那么記憶化遞歸（或動態(tài)規(guī)劃）帶來的收益會非常大。

為了消除這種重復計算，我們可使用查表的方式。即一邊遞歸一邊使用“記錄表”（比如哈希表或者數(shù)組）記錄我們已經(jīng)計算過的情況，當下次再次碰到的時候，如果之前已經(jīng)計算了，那么直接返回即可，這樣就避免了重復計算。下文要講的「動態(tài)規(guī)劃中 DP 數(shù)組其實和這里“記錄表”的作用是一樣的」。

如果你剛開始接觸遞歸，建議大家先去練習一下遞歸再往后看。一個簡單練習遞歸的方式是將你寫的迭代全部改成遞歸形式。比如你寫了一個程序，功能是“將一個字符串逆序輸出”，那么使用迭代將其寫出來會非常容易，那么你是否可以使用遞歸寫出來呢？通過這樣的練習，可以讓你逐步適應使用遞歸來寫程序。

當你已經(jīng)適應了遞歸的時候，那就讓我們繼續(xù)學習動態(tài)規(guī)劃吧！

動態(tài)規(guī)劃

講了這么多遞歸和記憶化，終于到了我們的主角登場了。

動態(tài)規(guī)劃的基本概念

我們先來學習動態(tài)規(guī)劃最重要的兩個概念：最優(yōu)子結(jié)構和無后效性。

其中：

無后效性決定了是否可使用動態(tài)規(guī)劃來解決。
最優(yōu)子結(jié)構決定了具體如何解決。

最優(yōu)子結(jié)構

動態(tài)規(guī)劃常常適用于有重疊子問題和最優(yōu)子結(jié)構性質(zhì)的問題。前面講了重疊子問題，那么最優(yōu)子結(jié)構是什么？這是我從維基百科找的定義：

如果問題的最優(yōu)解所包含的子問題的解也是最優(yōu)的，我們就稱該問題具有最優(yōu)子結(jié)構性質(zhì)（即滿足最優(yōu)化原理）。最優(yōu)子結(jié)構性質(zhì)為動態(tài)規(guī)劃算法解決問題提供了重要線索。

舉個例子：如果考試中的分數(shù)定義為 f，那么這個問題就可以被分解為語文，數(shù)學，英語等子問題。顯然子問題最優(yōu)的時候，總分這個大的問題的解也是最優(yōu)的。

再比如 01 背包問題：定義 f(weights, values, capicity)。如果我們想要求 f([1,2,3], [2,2,4], 10) 的最優(yōu)解。我們可以將其劃分為如下子問題：

將第三件物品裝進背包，也就是 f([1,2], [2,2], 10)
和不將第三件物品裝進背包，也就是 f([1,2,3], [2,2,4], 9)

?
顯然這兩個問題還是復雜，我們需要進一步拆解。不過，這里不是講如何拆解的。
?

原問題 f([1,2,3], [2,2,4], 10) 等于以上兩個子問題的最大值。只有兩個子問題都是「最優(yōu)的」時候整體才是最優(yōu)的，這是因為子問題之間不會相互影響。

無后效性

即子問題的解一旦確定，就不再改變，不受在這之后、包含它的更大的問題的求解決策影響。

繼續(xù)以上面兩個例子來說。

數(shù)學考得高不能影響英語（現(xiàn)實其實可能影響，比如時間一定，投入英語多，其他科目就少了）。
背包問題中 f([1,2,3], [2,2,4], 10) 選擇是否拿第三件物品，不應該影響是否拿前面的物品。比如題目規(guī)定了拿了第三件物品之后，第二件物品的價值就會變低或變高）。這種情況就不滿足無后向性。

動態(tài)規(guī)劃三要素

狀態(tài)定義

動態(tài)規(guī)劃的中心點是什么？如果讓我說的話，那就是「定義狀態(tài)」。

動態(tài)規(guī)劃解題的第一步就是定義狀態(tài)。定義好了狀態(tài)，就可以畫出遞歸樹，聚焦最優(yōu)子結(jié)構寫轉(zhuǎn)移方程就好了，因此我才說狀態(tài)定義是動態(tài)規(guī)劃的核心，動態(tài)規(guī)劃問題的狀態(tài)確實不容易看出。

但是一旦你能把狀態(tài)定義好了，那就可以順藤摸瓜畫出遞歸樹，畫出遞歸樹之后就聚焦最優(yōu)子結(jié)構就行了。但是能夠畫出遞歸樹的前提是：對問題進行劃分，專業(yè)點來說就是定義狀態(tài)。那怎么才能定義出狀態(tài)呢？

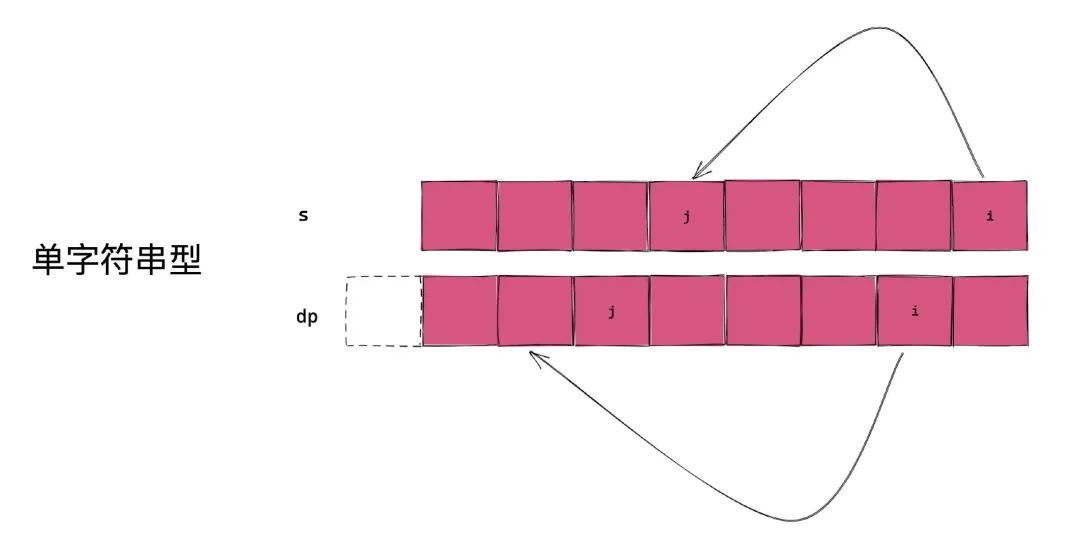
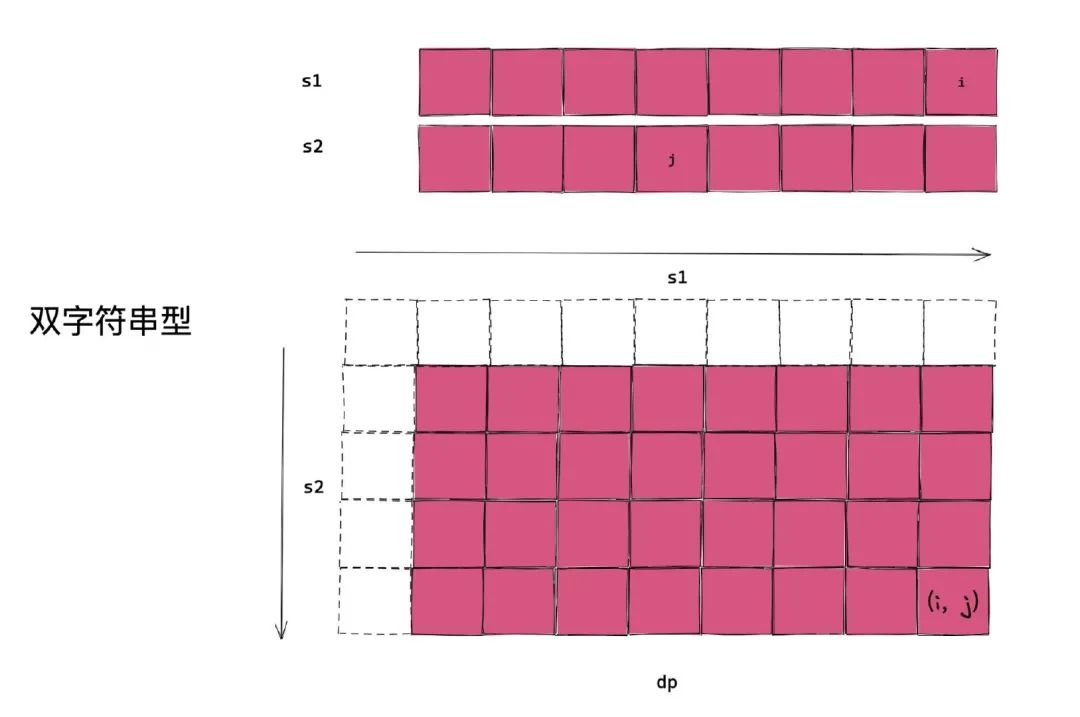
好在狀態(tài)的定義都有特點的套路。比如一個字符串的狀態(tài)，通常是 dp[i] 表示字符串 s 以 i 結(jié)尾的 ....。比如兩個字符串的狀態(tài)，通常是 dp[i][j] 表示字符串 s1 以 i 結(jié)尾，s2 以 j 結(jié)尾的 ....。

也就是說狀態(tài)的定義通常有不同的套路，大家可以在做題的過程中進行學習和總結(jié)。但是這種套路非常多，那怎么搞定呢？

說實話，只能多練習，在練習的過程中總結(jié)套路。具體的套路參考后面的「動態(tài)規(guī)劃的題型」 部分內(nèi)容。之后大家就可以針對不同的題型，去思考大概的狀態(tài)定義方向。

「兩個例子」

關于狀態(tài)定義，真的非常重要，以至于我將其列為動態(tài)規(guī)劃的核心。因此我覺得有必要舉幾個例子來進行說明。我直接從力扣的動態(tài)規(guī)劃專題^[1]中抽取前兩道給大家講講。

第一道題：《5. 最長回文子串》難度中等

給你一個字符串 s，找到 s 中最長的回文子串。

?

示例 1：

輸入：s =?"babad"
輸出："bab"
解釋："aba"?同樣是符合題意的答案。
示例 2：

輸入：s =?"cbbd"
輸出："bb"
示例 3：

輸入：s =?"a"
輸出："a"
示例 4：

輸入：s =?"ac"
輸出："a"
?

提示：

1?<=?s.length?<=?1000
s?僅由數(shù)字和英文字母（大寫和/或小寫）組成

「這道題入?yún)⑹且粋€字符串，那我們要將其轉(zhuǎn)化為規(guī)模更小的子問題，那無疑就是字符串變得更短的問題，臨界條件也應該是空字符串或者一個字符這樣。」

因此：

一種定義狀態(tài)的方式就是 f(s1)，含義是字符串 s1 的最長回文子串，其中 s1 就是題目中的字符串 s 的子串，那么答案就是 f(s)。
由于規(guī)模更小指的是字符串變得更短，而描述字符串我們也可以用兩個變量來描述，這樣實際上還省去了開辟字符串的開銷。兩個變量可以是「起點索引 + 子串長度」，也可以是「終點索引 + 子串長度」，也可以是「起點坐標 + 終點坐標」。隨你喜歡，這里我就用「起點坐標 + 終點坐標」。那么狀態(tài)定義就是 f(start, end)，含義是子串 s[start:end+1]的最長回文子串，那么答案就是 f(0, len(s) - 1)

?
s[start:end+1] 指的是包含 s[start]，而不包含 s[end+1] 的連續(xù)子串。
?

這無疑是一種定義狀態(tài)的方式，但是一旦我們這樣去定義就會發(fā)現(xiàn)：狀態(tài)轉(zhuǎn)移方程會變得難以確定（實際上很多動態(tài)規(guī)劃都有這個問題，比如最長上升子序列問題）。那究竟如何定義狀態(tài)呢？我會在稍后的狀態(tài)轉(zhuǎn)移方程繼續(xù)完成這道題。我們先來看下一道題。

第二道題：《10. 正則表達式匹配》難度困難

給你一個字符串?s?和一個字符規(guī)律?p，請你來實現(xiàn)一個支持?'.'?和?'*'?的正則表達式匹配。

'.'?匹配任意單個字符
'*'?匹配零個或多個前面的那一個元素
所謂匹配，是要涵蓋?整個?字符串 s的，而不是部分字符串。

?
示例 1：

輸入：s =?"aa"?p?=?"a"
輸出：false
解釋："a"?無法匹配?"aa"?整個字符串。
示例?2:

輸入：s =?"aa"?p?=?"a*"
輸出：true
解釋：因為?'*'?代表可以匹配零個或多個前面的那一個元素,?在這里前面的元素就是?'a'。因此，字符串?"aa"?可被視為?'a'?重復了一次。
示例 3：

輸入：s =?"ab"?p?=?".*"
輸出：true
解釋：".*"?表示可匹配零個或多個（'*'）任意字符（'.'）。
示例 4：

輸入：s =?"aab"?p?=?"c*a*b"
輸出：true
解釋：因為?'*'?表示零個或多個，這里?'c'?為?0?個,?'a'?被重復一次。因此可以匹配字符串?"aab"。
示例 5：

輸入：s =?"mississippi"?p?=?"mis*is*p*."
輸出：false
?

提示：

0?<=?s.length?<=?20
0?<=?p.length?<=?30
s 可能為空，且只包含從 a-z 的小寫字母。
p 可能為空，且只包含從 a-z 的小寫字母，以及字符 . 和?*。
保證每次出現(xiàn)字符?*?時，前面都匹配到有效的字符

這道題入?yún)⒂袃蓚€，一個是 s，一個是 p。沿用上面的思路，我們有兩種定義狀態(tài)的方式。

一種定義狀態(tài)的方式就是 f(s1, p1)，含義是 p1 是否可匹配字符串 s1，其中 s1 就是題目中的字符串 s 的子串，p1 就是題目中的字符串 p 的子串,那么答案就是 f(s, p)。
另一種是 f(s_start, s_end, p_start, p_end)，含義是子串 p1[p_start:p_end+1] 是否可以匹配字符串 s[s_start:s_end+1]，那么答案就是 f(0, len(s) - 1, 0, len(p) - 1)

而這道題實際上我們也可采用更簡單的狀態(tài)定義方式，不過基本思路都是差不多的。我仍舊賣個關子，后面講轉(zhuǎn)移方程再揭曉。

搞定了狀態(tài)定義，你會發(fā)現(xiàn)時間空間復雜度都變得很明顯了。這也是為啥我反復強調(diào)狀態(tài)定義是動態(tài)規(guī)劃的核心。

時間空間復雜度怎么個明顯法了呢？

首先空間復雜度，我剛才說了動態(tài)規(guī)劃其實就是查表的暴力法，因此動態(tài)規(guī)劃的空間復雜度打底就是表的大小。再直白一點就是上面的哈希表 memo 的大小。而 「memo」的大小基本就是狀態(tài)的個數(shù)。狀態(tài)個數(shù)是多少呢? 這不就取決你狀態(tài)怎么定義了么？比如上面的 f(s1, p1) 。狀態(tài)的多少是多少呢？很明顯就是每個參數(shù)的取值范圍大小的笛卡爾積。s1 的所有可能取值有 len(s) 種，p1 的所有可能有 len(p)種，那么總的狀態(tài)大小就是 len(s) * len(p)。那空間復雜度是，其中 m 和 n 分別為 s 和 p 的大小。

?
我說空間復雜度打底是狀態(tài)個數(shù)，這里暫時先不考慮狀態(tài)壓縮的情況。
?

其次是時間復雜度。時間復雜度就比較難說了。但是由于我們「無論如何都要枚舉所有狀態(tài)」，因此「時間復雜度打底就是狀態(tài)總數(shù)」。以上面的狀態(tài)定義方式，時間復雜度打底就是。

如果你枚舉每一個狀態(tài)都需要和 s 的每一個字符計算一下，那時間復雜度就是。

以上面的爬樓梯的例子來說，我們定義狀態(tài) f(n) 表示到達第 n 級臺階的方法數(shù)，那么狀態(tài)總數(shù)就是 n，空間復雜度和時間復雜度打底就是了。（仍然不考慮滾動數(shù)組優(yōu)化）

再舉個例子：62. 不同路徑

一個機器人位于一個 m x n 網(wǎng)格的左上角?（起始點在下圖中標記為“Start”?）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網(wǎng)格的右下角（在下圖中標記為“Finish”）。

問總共有多少條不同的路徑？

這道題是和上面的爬樓梯很像，只不過從一維變成了二維，我把它叫做「二維爬樓梯」，類似的換皮題還很多，大家慢慢體會。

這道題我定義狀態(tài)為 f(i, j) 表示機器人到達點 (i,j) 的總的路徑數(shù)。那么狀態(tài)總數(shù)就是 i 和 j 的取值的笛卡爾積，也就是 m * n 。

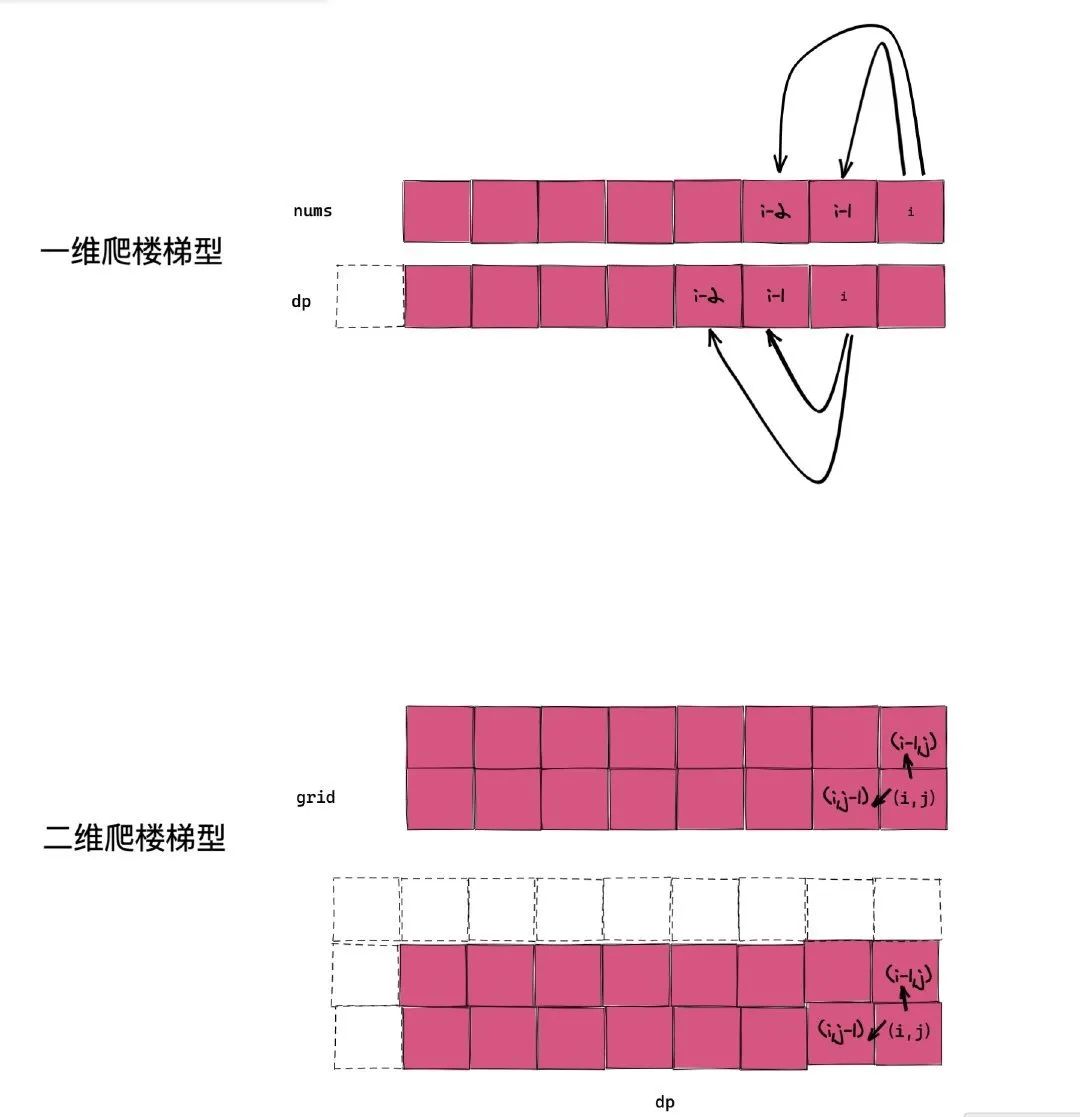
總的來說，動態(tài)規(guī)劃的空間和時間復雜度「打底就是狀態(tài)的個數(shù)」，而狀態(tài)的個數(shù)通常是參數(shù)的笛卡爾積，這是由動態(tài)規(guī)劃的無后向性決定的。

「臨界條件是比較最容易的」

當你定義好了狀態(tài)，剩下就三件事了：

臨界條件
狀態(tài)轉(zhuǎn)移方程
枚舉狀態(tài)

在上面講解的爬樓梯問題中，如果我們用 f(n) 表示爬 n 級臺階有多少種方法的話，那么：

f(1)?與?f(2)?就是【邊界】
f(n)?=?f(n-1)?+?f(n-2)?就是【狀態(tài)轉(zhuǎn)移公式】

我用動態(tài)規(guī)劃的形式表示一下：

dp[0]?與?dp[1]?就是【邊界】
dp[n]?=?dp[n?-?1]?+?dp[n?-?2]?就是【狀態(tài)轉(zhuǎn)移方程】

可以看出記憶化遞歸和動態(tài)規(guī)劃是多么的相似。

實際上臨界條件相對簡單，大家只有多刷幾道題，里面就有感覺。困難的是找到狀態(tài)轉(zhuǎn)移方程和枚舉狀態(tài)。這兩個核心點的都建立在「已經(jīng)抽象好了狀態(tài)」的基礎上。比如爬樓梯的問題，如果我們用 f(n) 表示爬 n 級臺階有多少種方法的話，那么 f(1), f(2), ... 就是各個「獨立的狀態(tài)」。

搞定了狀態(tài)的定義，那么我們來看下狀態(tài)轉(zhuǎn)移方程。

狀態(tài)轉(zhuǎn)移方程

動態(tài)規(guī)劃中當前階段的狀態(tài)往往是上一階段狀態(tài)和上一階段決策的結(jié)果。這里有兩個關鍵字，分別是：

上一階段狀態(tài)
上一階段決策

也就是說，如果給定了第 k 階段的狀態(tài) s[k] 以及決策 choice(s[k])，則第 k+1 階段的狀態(tài) s[k+1] 也就完全確定，用公式表示就是：s[k] + choice(s[k]) -> s[k+1]，這就是狀態(tài)轉(zhuǎn)移方程。需要注意的是 choice 可能有多個，因此每個階段的狀態(tài) s[k+1]也會有多個。

繼續(xù)以上面的爬樓梯問題來說，爬樓梯問題由于上第 n 級臺階一定是從 n - 1 或者 n - 2 來的，因此上第 n 級臺階的數(shù)目就是 上 n - 1 級臺階的數(shù)目加上 n - 1 級臺階的數(shù)目。

上面的這個理解是核心，它就是我們的狀態(tài)轉(zhuǎn)移方程，用代碼表示就是 f(n) = f(n - 1) + f(n - 2)。

實際操作的過程，有可能題目和爬樓梯一樣直觀，我們不難想到。也可能隱藏很深或者維度過高。如果你實在想不到，可以嘗試畫圖打開思路，這也是我剛學習動態(tài)規(guī)劃時候的方法。當你做題量上去了，你的題感就會來，那個時候就可以不用畫圖了。

比如我們定義了狀態(tài)方程，據(jù)此我們定義初始狀態(tài)和目標狀態(tài)。然后聚焦最優(yōu)子結(jié)構，「思考每一個狀態(tài)究竟如何進行擴展使得離目標狀態(tài)越來越近」。

如下圖所示：

理論差不多先這樣，接下來來幾個實戰(zhàn)消化一下。

ok，接下來是解密環(huán)節(jié)。上面兩道題我們都沒有講轉(zhuǎn)移方程，我們在這里補上。

第一道題：《5. 最長回文子串》難度中等。上面我們的兩種狀態(tài)定義都不好，而我可以在上面的基礎上「稍微變動一點」就可以使得轉(zhuǎn)移方程變得非常好寫。這個技巧在很多動態(tài)題目都有體現(xiàn)，比如最長上升子序列等，「需要大家掌握」。

以上面提到的 f(start, end) 來說，含義是子串 s[start:end+1]的最長回文子串。表示方式我們不變，只是將含義變成子串 s[start:end+1]的最長回文子串，「且必須包含 start 和 end」。經(jīng)過這樣的定義，實際上我們也沒有必要定義 f(start, end)的返回值是長度了，而僅僅是布爾值就行了。如果返回 true，則最長回文子串就是 end - start + 1，否則就是 0。

這樣轉(zhuǎn)移方程就可以寫為：

f(i,j)=f(i+1,j?1)?and?s[i]?==?s[j]

第二道題：《10. 正則表達式匹配》難度困難。

以我們分析的 f(s_start, s_end, p_start, p_end) 來說，含義是子串 p1[p_start:p_end+1] 是否可以匹配字符串 s[s_start:s_end+1]。

實際上，我們可以定義更簡單的方式，那就是 f(s_end, p_end)，含義是子串 p1[:p_end+1] 是否可以匹配字符串 s[:s_end+1]。也就是說固定起點為索引 0，這同樣也是一個「很常見的技巧，請務必掌握。」

這樣轉(zhuǎn)移方程就可以寫為：

if p[j] 是小寫字母，是否匹配取決于 s[i] 是否等于 p[j]:

if p[j] == '.'，一定可匹配:

f(i,j)=f(i-1,j?1)

if p[j] == '*'，表示 p 可以匹配 s 第 j?1 個字符匹配任意次：

相信你能分析到這里，寫出代碼就不是難事了。具體代碼可參考我的力扣題解倉庫^[2]，咱就不在這里講了。

注意到了么？所有的狀態(tài)轉(zhuǎn)移方程我都使用了上述的數(shù)學公式來描述。沒錯，所有的轉(zhuǎn)移方程都可以這樣描述。我建議大家「做每一道動態(tài)規(guī)劃題目都寫出這樣的公式」，起初你可能覺得很煩麻煩。不過相信我，你堅持下去，會發(fā)現(xiàn)自己慢慢變強大。就好像我強烈建議你每一道題都分析好復雜度一樣。動態(tài)規(guī)劃不僅要搞懂轉(zhuǎn)移方程，還要自己像我那樣完整地用數(shù)學公式寫出來。

是不是覺得狀態(tài)轉(zhuǎn)移方程寫起來麻煩？這里我給大家介紹一個小技巧，那就是使用 latex，latex 語法可以方便地寫出這樣的公式。另外西法還貼心地寫了「一鍵生成動態(tài)規(guī)劃轉(zhuǎn)移方程公式」的功能，幫助大家以最快速度生成公訴處。插件地址：https://leetcode-pp.github.io/leetcode-cheat/?tab=solution-template

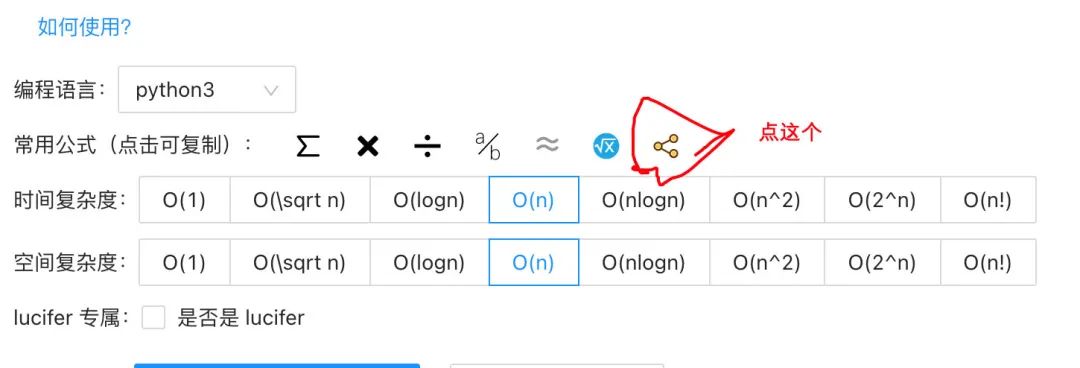
狀態(tài)轉(zhuǎn)移方程實在是沒有什么靈丹妙藥，不同的題目有不同的解法。狀態(tài)轉(zhuǎn)移方程同時也是解決動態(tài)規(guī)劃問題中最最困難和關鍵的點，大家一定要多多練習，提高題感。接下來，我們來看下不那么困難，但是新手疑問比較多的問題 - 「如何枚舉狀態(tài)」。

當然狀態(tài)轉(zhuǎn)移方程可能不止一個，不同的轉(zhuǎn)移方程對應的效率也可能大相徑庭，這個就是比較玄學的話題了，需要大家在做題的過程中領悟。

如何枚舉狀態(tài)

前面說了如何枚舉狀態(tài)，才能不重不漏是枚舉狀態(tài)的關鍵所在。

如果是一維狀態(tài)，那么我們使用一層循環(huán)可以搞定。

for?i?in?range(1,?n?+?1):
??pass

如果是兩維狀態(tài)，那么我們使用兩層循環(huán)可以搞定。

for?i?in?range(1,?m?+?1):
??for?j?in?range(1,?n?+?1):
????pass

。。。

但是實際操作的過程有很多細節(jié)比如:

一維狀態(tài)我是先枚舉左邊的還是右邊的？（從左到右遍歷還是從右到左遍歷）
二維狀態(tài)我是先枚舉左上邊的還是右上的，還是左下的還是右下的？
里層循環(huán)和外層循環(huán)的位置關系（可以互換么）
。。。

其實這個東西和很多因素有關，很難總結(jié)出一個規(guī)律，而且我認為也完全沒有必要去總結(jié)規(guī)律。

不過這里我還是總結(jié)了一個關鍵點，那就是：

「如果你沒有使用滾動數(shù)組的技巧」，那么遍歷順序取決于狀態(tài)轉(zhuǎn)移方程。比如:

for?i?in?range(1,?n?+?1):
??dp[i]?=?dp[i?-?1]?+?1

那么我們就需要從左到右遍歷，原因很簡單，因為 dp[i] 依賴于 dp[i - 1]，因此計算 dp[i] 的時候， dp[i - 1] 需要已經(jīng)計算好了。

?
二維的也是一樣的，大家可以試試。
?

「如果你使用了滾動數(shù)組的技巧」，則怎么遍歷都可以，但是不同的遍歷意義通常不不同的。比如我將二維的壓縮到了一維：

for?i?in?range(1,?n?+?1):
??for?j?in?range(1,?n?+?1):
????dp[j]?=?dp[j?-?1]?+?1;

這樣是可以的。dp[j - 1] 實際上指的是壓縮前的 dp[i][j - 1]

而：

for?i?in?range(1,?n?+?1):
??#??倒著遍歷
??for?j?in?range(n,?0,?-1):
????dp[j]?=?dp[j?-?1]?+?1;

這樣也是可以的。但是 dp[j - 1] 實際上指的是壓縮前的 dp[i - 1][j - 1]。因此實際中采用怎么樣的遍歷手段取決于題目。我特意寫了一個【完全背包問題】套路題（1449. 數(shù)位成本和為目標值的最大數(shù)字文章，通過一個具體的例子告訴大家不同的遍歷有什么實際不同，強烈建議大家看看，并順手給個三連。

關于里外循環(huán)的問題，其實和上面原理類似。

這個比較微妙，大家可以參考這篇文章理解一下 0518.coin-change-2。

小結(jié)

關于如何確定臨界條件通常是比較簡單的，多做幾個題就可以快速掌握。

關于如何確定狀態(tài)轉(zhuǎn)移方程，這個其實比較困難。不過所幸的是，這些套路性比較強，比如一個字符串的狀態(tài)，通常是 dp[i] 表示字符串 s 以 i 結(jié)尾的 ....。比如兩個字符串的狀態(tài)，通常是 dp[i][j] 表示字符串 s1 以 i 結(jié)尾，s2 以 j 結(jié)尾的 ....。這樣遇到新的題目可以往上套，實在套不出那就先老實畫圖，不斷觀察，提高題感。

關于如何枚舉狀態(tài)，如果沒有滾動數(shù)組，那么根據(jù)轉(zhuǎn)移方程決定如何枚舉即可。如果用了滾動數(shù)組，那么要注意壓縮后和壓縮前的 dp 對應關系即可。

動態(tài)規(guī)劃 VS 記憶化遞歸

上面我們用記憶化遞歸的問題巧妙地解決了爬樓梯問題。那么動態(tài)規(guī)劃是怎么解決這個問題呢？

答案也是“查表”，我們平常寫的 dp table 就是表，其實這個 dp table 和上面的 memo 沒啥差別。

而一般我們寫的 dp table，「數(shù)組的索引通常對應記憶化遞歸的函數(shù)參數(shù)，值對應遞歸函數(shù)的返回值。」

看起來兩者似乎「沒任何思想上的差異，區(qū)別的僅僅是寫法」？？沒錯。不過這種寫法上的差異還會帶來一些別的相關差異，這點我們之后再講。

如果上面的爬樓梯問題，使用動態(tài)規(guī)劃，代碼是怎么樣的呢？我們來看下：

function?climbStairs(n)?{
??if?(n?==?1)?return?1;
??const?dp?=?new?Array(n);
??dp[0]?=?1;
??dp[1]?=?2;

??for?(let?i?=?2;?i?????dp[i]?=?dp[i?-?1]?+?dp[i?-?2];
??}
??return?dp[dp.length?-?1];
}

大家現(xiàn)在不會也沒關系，我們將「前文的遞歸的代碼稍微改造一下」。其實就是將函數(shù)的名字改一下：

function?dp(n)?{
??if?(n?===?1)?return?1;
??if?(n?===?2)?return?2;
??return?dp(n?-?1)?+?dp(n?-?2);
}

經(jīng)過這樣的變化。我們將 dp[n] 和 dp(n) 對比看，這樣是不是有點理解了呢? 其實他們的區(qū)別只不過是「遞歸用調(diào)用棧枚舉狀態(tài)，而動態(tài)規(guī)劃使用迭代枚舉狀態(tài)。」

?
如果需要多個維度枚舉，那么記憶化遞歸內(nèi)部也可以使用迭代進行枚舉，比如最長上升子序列問題。
?

動態(tài)規(guī)劃的查表過程如果畫成圖，就是這樣的：

?
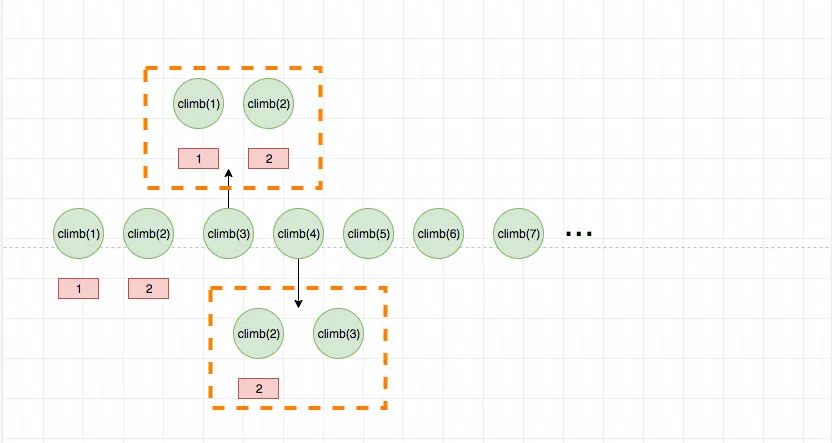
虛線代表的是查表過程
?

滾動數(shù)組優(yōu)化

爬樓梯我們并沒有必要使用一維數(shù)組，而是借助兩個變量來實現(xiàn)的，空間復雜度是 O(1)。代碼：

function?climbStairs(n)?{
??if?(n?===?1)?return?1;
??if?(n?===?2)?return?2;

??let?a?=?1;
??let?b?=?2;
??let?temp;

??for?(let?i?=?3;?i?<=?n;?i++)?{
????temp?=?a?+?b;
????a?=?b;
????b?=?temp;
??}

??return?temp;
}

之所以能這么做，是因為爬樓梯問題的狀態(tài)轉(zhuǎn)移方程中「當前狀態(tài)只和前兩個狀態(tài)有關」，因此只需要存儲這兩個即可。動態(tài)規(guī)劃問題有很多這種討巧的方式，這個技巧叫做滾動數(shù)組。

這道題目是動態(tài)規(guī)劃中最簡單的問題了，因為僅涉及到單個因素的變化，如果涉及到多個因素，就比較復雜了，比如著名的背包問題，挖金礦問題等。

對于單個因素的，我們最多只需要一個一維數(shù)組即可，對于如背包問題我們需要二維數(shù)組等更高緯度。

回答上面的問題：記憶化遞歸和動態(tài)規(guī)劃除了一個用遞歸一個用迭代，其他沒差別。那兩者有啥區(qū)別呢？我覺得最大的區(qū)別就是記憶化遞歸無法使用滾動數(shù)組優(yōu)化（不信你用上面的爬樓梯試一下），記憶化調(diào)用棧的開銷比較大（復雜度不變，你可以認為空間復雜度常數(shù)項更大），不過幾乎不至于 TLE 或者 MLE。「因此我的建議就是沒空間優(yōu)化需求直接就記憶化，否則用迭代 dp」。

再次強調(diào)一下：

如果說遞歸是從問題的結(jié)果倒推，直到問題的規(guī)模縮小到尋常。那么動態(tài)規(guī)劃就是從尋常入手，逐步擴大規(guī)模到最優(yōu)子結(jié)構。
記憶化遞歸和動態(tài)規(guī)劃沒有本質(zhì)不同。都是枚舉狀態(tài)，并根據(jù)狀態(tài)直接的聯(lián)系逐步推導求解。
動態(tài)規(guī)劃性能通常更好。一方面是遞歸的棧開銷，一方面是滾動數(shù)組的技巧。

動態(tài)規(guī)劃的基本類型

背包 DP（這個我們專門開了一個專題講）
區(qū)間 DP

區(qū)間類動態(tài)規(guī)劃是線性動態(tài)規(guī)劃的擴展，它在分階段地劃分問題時，與階段中元素出現(xiàn)的順序和由前一階段的哪些元素合并而來有很大的關系。令狀態(tài) 表示將下標位置到的所有元素合并能獲得的價值的最大值，那么，為將這兩組元素合并起來的代價。

區(qū)間 DP 的特點：

「合并」：即將兩個或多個部分進行整合，當然也可以反過來；

「特征」：能將問題分解為能兩兩合并的形式；

「求解」：對整個問題設最優(yōu)值，枚舉合并點，將問題分解為左右兩個部分，最后合并兩個部分的最優(yōu)值得到原問題的最優(yōu)值。

推薦兩道題：

877. 石子游戲
312. 戳氣球
狀壓 DP

關于狀壓 DP 可以參考下我之前寫過的一篇文章：狀壓 DP 是什么？這篇題解帶你入門

數(shù)位 DP

數(shù)位 DP 通常是這：給定一個閉區(qū)間，讓你求這個區(qū)間中滿足「某種條件」的數(shù)的總數(shù)。

推薦一道題 Increasing-Digits

計數(shù) DP 和概率 DP

這兩個我就不多說。因為沒啥規(guī)律。

之所以列舉計數(shù) DP 是因為兩個原因：

讓大家知道確實有這個題型。
計數(shù)是動態(tài)規(guī)劃的副產(chǎn)物。

概率 DP 比較特殊，概率 DP 的狀態(tài)轉(zhuǎn)移公式一般是說一個狀態(tài)有多大的概率從某一個狀態(tài)轉(zhuǎn)移過來，更像是期望的計算，因此也叫期望 DP。

91. 解碼方法
837. 新 21 點

更多題目類型以及推薦題目見刷題插件的學習路線。插件獲取方式：公眾號力扣加加回復插件。

什么時候用記憶化遞歸？

從數(shù)組兩端同時進行遍歷的時候使用記憶化遞歸方便，其實也就是區(qū)間 DP（range dp）。比如石子游戲，再比如這道題 https://binarysearch.com/problems/Make-a-Palindrome-by-Inserting-Characters

如果區(qū)間 dp 你的遍歷方式大概需要這樣：

class?Solution:
????def?solve(self,?s):
????????n?=?len(s)
????????dp?=?[[0]?*?n?for?_?in?range(n)]
????????#?右邊界倒序遍歷
????????for?i?in?range(n?-?1,?-1,?-1):
????????????#?左邊界正序遍歷
????????????for?j?in?range(i?+?1,?n):
????????????????#?do?something
????????return??dp[0][m-1]?#?一般都是使用這個區(qū)間作為答案

如果使用記憶化遞歸則不需考慮遍歷方式的問題。

代碼：

class?Solution:
????def?solve(self,?s):
????????@lru_cache(None)
????????def?helper(l,?r):
????????????if?l?>=?r:
????????????????return?0

????????????if?s[l]?==?s[r]:
????????????????return?helper(l?+?1,?r?-?1)

????????????return?1?+?min(helper(l?+?1,?r),?helper(l,?r?-?1))

????????return?helper(0,?len(s)?-?1)

「選擇」 比較離散的時候，使用記憶化遞歸更好。比如馬走棋盤。

那什么時候不用記憶化遞歸呢？答案是其他情況都不用。因為普通的 dp table 有一個重要的功能，這個功能記憶化遞歸是無法代替的，那就是「滾動數(shù)組優(yōu)化」。如果你需要對空間進行優(yōu)化，那一定要用 dp table。

熱身開始

理論知識已經(jīng)差不多了，我們拿一道題來試試手。

我們以一個非常經(jīng)典的背包問題來練一下手。

題目：322. 零錢兌換^[3]

給定不同面額的硬幣 coins 和一個總金額 amount。編寫一個函數(shù)來計算可以湊成總金額所需的最少的硬幣個數(shù)。如果沒有任何一種硬幣組合能組成總金額，返回?-1。

你可以認為每種硬幣的數(shù)量是無限的。

?

示例 1：

輸入：coins =?[1, 2, 5], amount = 11
輸出：3
解釋：11 = 5 + 5 + 1

這道題的參數(shù)有兩個，一個是 coins，一個是 amount。

我們可以定義狀態(tài)為 f(i, j) 表示用 coins 的前 i 項找 j 元需要的最少硬幣數(shù)。那么答案就是 f(len(coins) - 1, amount)。

由組合原理，coins 的所有選擇狀態(tài)是。狀態(tài)總數(shù)就是 i 和 j 的取值的笛卡爾積，也就是 2^len(coins) * (amount + 1)。

?
減 1 是因為存在 0 元的情況。
?

明確了這些，我們需要考慮的就是狀態(tài)如何轉(zhuǎn)移，也就是如何從尋常轉(zhuǎn)移到 f(len(coins) - 1, amount)。

如何確定狀態(tài)轉(zhuǎn)移方程？我們需要:

聚焦最優(yōu)子結(jié)構
做選擇，在選擇中取最優(yōu)解（如果是計數(shù) dp 則進行計數(shù)）

對于這道題來說，我們的選擇有兩種：

選擇 coins[i]
不選擇 coins[i]

這無疑是完備的。只不過僅僅是對 coins 中的每一項進行「選擇與不選擇」，這樣的狀態(tài)數(shù)就已經(jīng)是了，其中 n 為 coins 長度。

如果僅僅是這樣枚舉肯定會超時，因為狀態(tài)數(shù)已經(jīng)是指數(shù)級別了。

而這道題的核心在于 coins[i] 選擇與否其實沒有那么重要，「重要的其實是選擇的 coins 一共有多少錢」。

因此我們可以定義 f(i, j) 表示選擇了 coins 的前 i 項（怎么選的不關心），且組成 j 元需要的最少硬幣數(shù)。

舉個例子來說，比如 coins = [1,2,3] 。那么選擇 [1,2] 和選擇 [3] 雖然是不一樣的狀態(tài)，但是我們壓根不關心。因為這兩者沒有區(qū)別，我們還是誰對結(jié)果貢獻大就 pick 誰。

以 coins = [1,2,3], amount = 6 來說，我們可以畫出如下的遞歸樹。

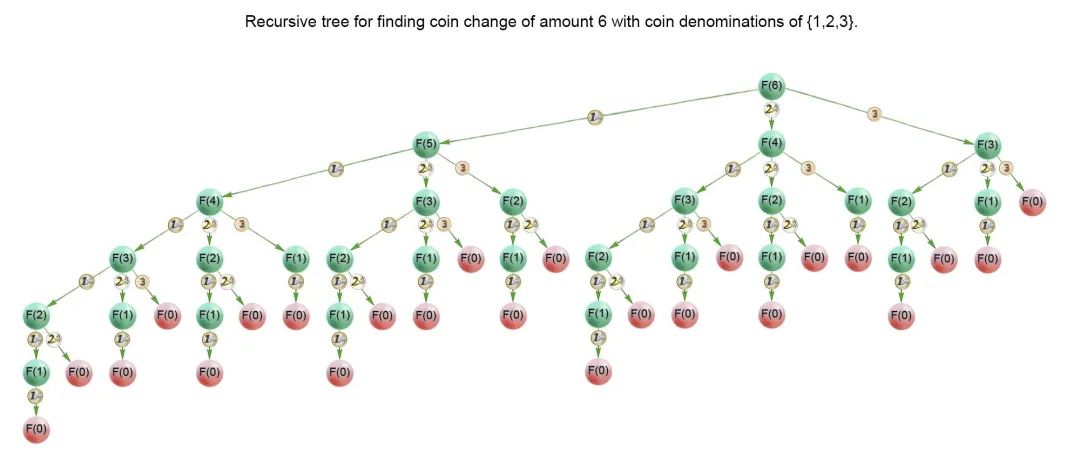
（圖片來自https://leetcode.com/problems/coin-change/solution/）

因此轉(zhuǎn)移方程就是 min(dp[i][j], dp[i-1][j - coins[j]] + 1)，含義就是：min(不選擇 coins[j], 選擇 coins[j]) 所需最少的硬幣數(shù)。

用公式表示就是：

?
amount 表示無解。因為硬幣的面額都是正整數(shù)，不可能存在一種需要 amount + 1 枚硬幣的方案。
?

「代碼」

記憶化遞歸：

class?Solution:
????def?coinChange(self,?coins:?List[int],?amount:?int)?->?int:
????????@lru_cache(None)
????????def?dfs(amount):
????????????if?amount?0:?return?float('inf')
????????????if?amount?==?0:?return?0
????????????ans?=?float('inf')
????????????for?coin?in?coins:
????????????????ans?=?min(ans,?1?+?dfs(amount?-?coin))
????????????return?ans
????????ans?=?dfs(amount)
????????return?-1?if?ans?==?float('inf')?else?ans

二維 dp:



class?Solution:
????def?coinChange(self,?coins:?List[int],?amount:?int)?->?int:
????????if?amount?0:
????????????return?-?1
????????dp?=?[[amount?+?1?for?_?in?range(len(coins)?+?1)]
??????????????for?_?in?range(amount?+?1)]
????????#?初始化第一行為0，其他為最大值（也就是amount?+?1）

????????for?j?in?range(len(coins)?+?1):
????????????dp[0][j]?=?0

????????for?i?in?range(1,?amount?+?1):
????????????for?j?in?range(1,?len(coins)?+?1):
????????????????if?i?-?coins[j?-?1]?>=?0:
????????????????????dp[i][j]?=?min(
????????????????????????dp[i][j?-?1],?dp[i?-?coins[j?-?1]][j]?+?1)
????????????????else:
????????????????????dp[i][j]?=?dp[i][j?-?1]

????????return?-1?if?dp[-1][-1]?==?amount?+?1?else?dp[-1][-1]

dp[i][j] 依賴于dp[i][j - 1]和 dp[i - coins[j - 1]][j] + 1) 這是一個優(yōu)化的信號，我們可以將其優(yōu)化到一維。

一維 dp（滾動數(shù)組優(yōu)化）：

class?Solution:
????def?coinChange(self,?coins:?List[int],?amount:?int)?->?int:
????????dp?=?[amount?+?1]?*?(amount?+?1)
????????dp[0]?=?0

????????for?j?in?range(len(coins)):
????????????for?i?in?range(1,?amount?+?1):
????????????????if?i?>=?coins[j]:
????????????????????dp[i]?=?min(dp[i],?dp[i?-?coins[j]]?+?1)

????????return?-1?if?dp[-1]?==?amount?+?1?else?dp[-1]

總結(jié)

本篇文章總結(jié)了算法中比較常用的兩個方法 - 遞歸和動態(tài)規(guī)劃。遞歸的話可以拿樹的題目練手，動態(tài)規(guī)劃的話則將我上面推薦的刷完，再考慮去刷力扣的動態(tài)規(guī)劃標簽即可。

大家前期學習動態(tài)規(guī)劃的時候，可以先嘗試使用記憶化遞歸解決。然后將其改造為動態(tài)規(guī)劃，這樣多練習幾次就會有感覺。之后大家可以練習一下滾動數(shù)組，這個技巧很有用，并且相對來說比較簡單。

動態(tài)規(guī)劃的核心在于定義狀態(tài)，定義好了狀態(tài)其他都是水到渠成。

動態(tài)規(guī)劃的難點在于「枚舉所有狀態(tài)（不重不漏）」 和 「尋找狀態(tài)轉(zhuǎn)移方程」。

參考

oi-wiki - dp 這個資料推薦大家學習，非常全面。只不過更適合有一定基礎的人，大家可以配合本講義食用哦。

另外，大家可以去 LeetCode 探索中的遞歸 I 中進行互動式學習。

Reference

[1]

動態(tài)規(guī)劃專題: https://leetcode-cn.com/tag/dynamic-programming/problemset/

[2]

力扣題解倉庫: https://github.com/azl397985856/leetcode

[3]

322. 零錢兌換: https://leetcode-cn.com/problems/coin-change/

大廠面試常被問到的動態(tài)規(guī)劃

記憶化遞歸

什么是遞歸？

不僅僅是普通的遞歸函數(shù)

什么是記憶化？

小結(jié)

動態(tài)規(guī)劃

動態(tài)規(guī)劃的基本概念

最優(yōu)子結(jié)構

無后效性

動態(tài)規(guī)劃三要素

狀態(tài)定義

狀態(tài)轉(zhuǎn)移方程

如何枚舉狀態(tài)

小結(jié)

動態(tài)規(guī)劃 VS 記憶化遞歸

滾動數(shù)組優(yōu)化

動態(tài)規(guī)劃的基本類型

什么時候用記憶化遞歸？

熱身開始

推薦練習題目

總結(jié)

參考

Reference