基于branch and bound插入的large neighborhood search

代碼黑科技的分享區(qū)
 ?
?一、前言
今年開年那會還在做一個課題的實驗,那時候想用large neighborhood search來做一個問題,但是后來發(fā)現(xiàn)常規(guī)的一些repair、destroy算子效果并不是很好。后來才知道,large neighborhood search以及它的衍生算法,這類框架給人一種非常通用的感覺,就是無論啥問題都能往里面套。
往往的結(jié)果是套進(jìn)去效果也是一般。這也是很多剛?cè)胄械男』锇榻?jīng)常喜歡干的事吧,各種算法框架套一個問題,發(fā)現(xiàn)結(jié)果不好了就感覺換下一個。最后復(fù)現(xiàn)了N多個算法發(fā)現(xiàn)依然no process,這時候就會懷疑人生了。其實要想取得好的performance,肯定還是要推導(dǎo)一些問題特性,設(shè)計相應(yīng)的算子也好,鄰域結(jié)構(gòu)也好。
好了,回到正題。當(dāng)時我試了好幾個large neighborhood search算子,發(fā)現(xiàn)沒啥效果的時候,心里難受得很。那幾天晚上基本上是轉(zhuǎn)輾反側(cè),難以入眠,當(dāng)然了是在思考問題。然后一個idea突然浮現(xiàn)在我的腦瓜子里,常規(guī)的repair算子難以在問題中取得好的performance,是因為約束太多了,插入的時候很容易違背約束。

在不違背約束的條件下又難以提升解的質(zhì)量,我就想能不能插入的啥時候采取branch and bound。遍歷所有的可能插入方式,然后記錄過程中的一個upper bound用來刪掉一些分支。
感覺是有搞頭的,后來想想,這個branch的方法以及bound的方法似乎是有點難設(shè)計。然后又?jǐn)R置了幾天,最后沒進(jìn)展的時候突然找了一篇論文,是好多年前的一篇文章了。里面詳細(xì)講解了large neighborhood search中如何利用branch and bound進(jìn)行插入,后來實現(xiàn)了以下感覺還可以。感覺這個方法還是有一定的參考價值的,因此今天就來寫寫(其實當(dāng)時就想寫了,只不過一直拖到了現(xiàn)在。。。)
二、large neighborhood search關(guān)于這個算法,我在此前的推文中已經(jīng)有過相應(yīng)的介紹,詳情小伙伴們可以戳這篇的鏈接進(jìn)行查看:
自適應(yīng)大鄰域搜索(Adaptive Large Neighborhood Search)入門到精通超詳細(xì)解析-概念篇
我把其中的一段話摘出來:
大多數(shù)鄰域搜索算法都明確定義它們的鄰域。在LNS中,鄰域是由和方法隱式定義的。方法會破壞當(dāng)前解的一部分,而后方法會對被破壞的解進(jìn)行重建。方法通常包含隨機(jī)性的元素,以便在每次調(diào)用方法時破壞解的不同部分。
那么,解的鄰域就可以定義為:首先通過利用方法破壞解,然后利用方法重建解,從而得到的一系列解的集合。LNS算法框架如下:

有關(guān)該算法更詳細(xì)的介紹可以參考Handbook Of Metaheuristics這本書2019版本中的Chapter 4 Large Neighborhood Search(David Pisinger and Stefan Ropke),文末我會放出下載的鏈接。
關(guān)于destroy算子呢,有很多種,比如隨機(jī)移除幾個點,貪心移除一些比較差的點,或者基于后悔值排序移除一些點等,這里我給出文獻(xiàn)中的一種移除方式,Shaw (1998)提出的基于進(jìn)行移除:

假設(shè)需要從解中所有的移除個,它首先隨機(jī)選擇一個放進(jìn)(已經(jīng)移除的列表)(第1行),然后迭代地(3–6行)移除剩下的個。每次這樣的迭代都會先從中隨機(jī)選擇一個,并根據(jù)相關(guān)標(biāo)準(zhǔn)對其余未移除的進(jìn)行排序(第3-4行)。在第5行中計算要插入的新的下標(biāo),然后插入到中(第6行),直到迭代結(jié)束。關(guān)聯(lián)度的定義如Shaw(1998)所述:
其中,customer 和 在不同的路徑中時,否則為0。
三、branch and bound上面講了Large Neighborhood Search以及介紹了一個方法,下面就是重頭戲,如何利用branch and bound進(jìn)行插入了。
3.1 branch
其實插入的分支方式還是挺好設(shè)計的,這玩意兒呢我將也比較難講清楚,我就畫圖好了,還是基于VRP問題示例,其他問題類似,假如我們現(xiàn)在有這樣一個解:
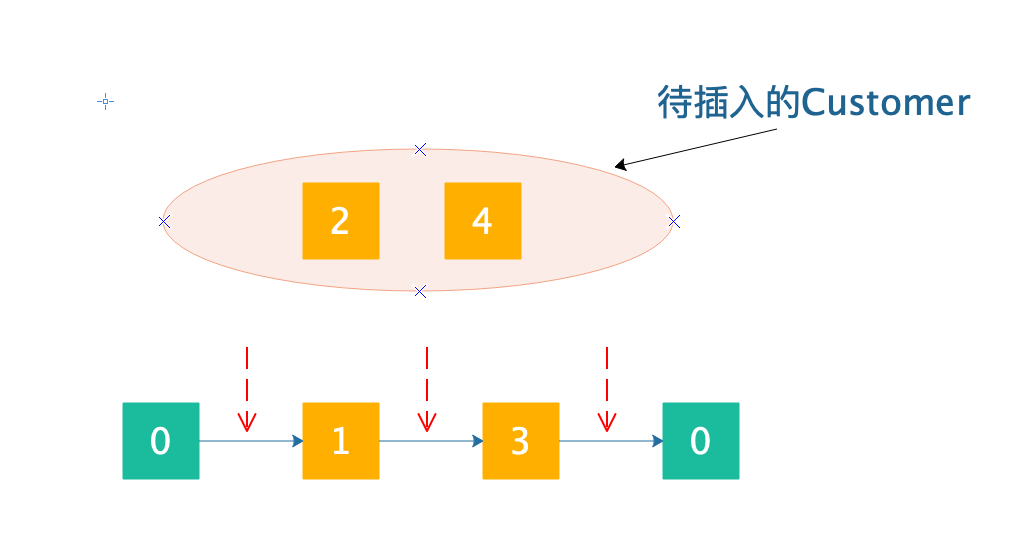
為了演示我就不畫太多點太多路徑了,免得大家看得心累。
紅色箭頭就是能夠插入的位置。現(xiàn)在,假如我們插入(由于branch and bound是需要遍歷所有可能的插入組合,因此先插入哪個后插入哪個都是可以的,但是分支定界的速度可能會受到很大的影響,這個咱們暫時不討論):
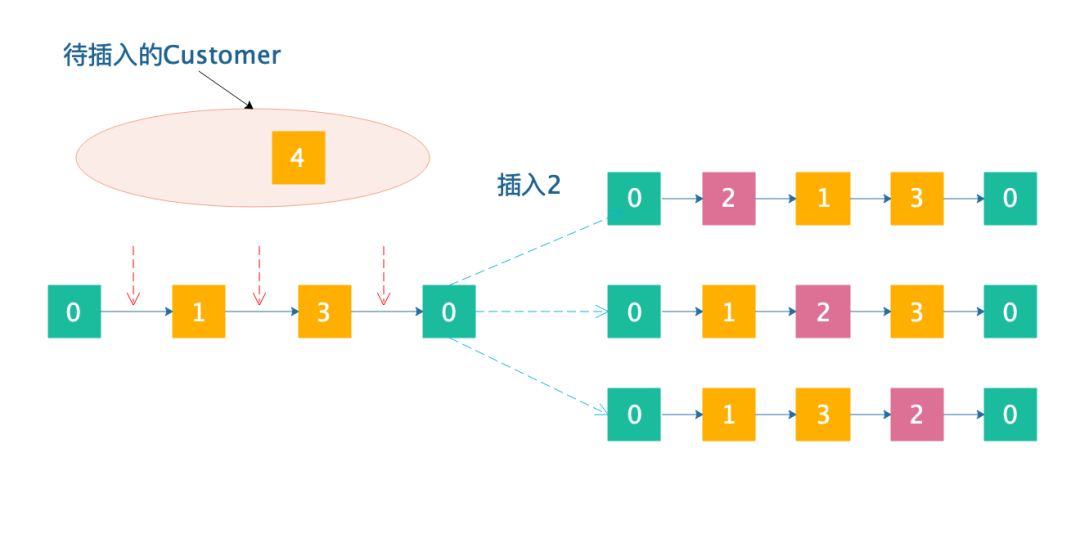
為了讓大家看得更加清楚,我把的位置用粉紅色給標(biāo)記出來了,一共有3條分支,有個候選的位置就有多少條分支。
現(xiàn)在,還剩下,插入的時候,我們需要繼續(xù)進(jìn)行分支:
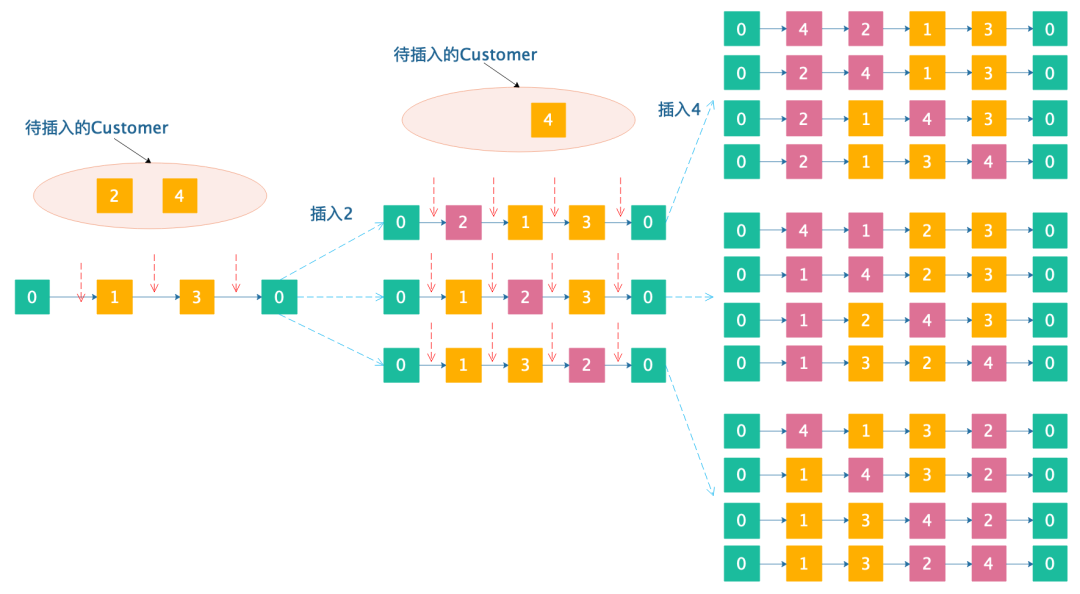
55~畫分支樹真是畫死我啦(大家一定要給個贊,點個在看呀~),可以看到,最后每條路徑就是一個完成的解。在兩個點的插入兩個點最后分支完成的居然有12個!!!大家可以自行腦補(bǔ)下,在90個點的中插入10個點最終形成的分支會有多少。毫無疑問會很多很多,多到你無法想象。下面是DFS搜索分支樹的過程:

如果要插入的客戶組為空,則可以認(rèn)為所有客戶已經(jīng)插入到solution中,形成了一個,因此判斷找到的一個upper bound是否比最優(yōu)的upper bound還要好,是的話就對upper bound進(jìn)行更新。否則,它會選擇插入效果最好的客戶,這會使目標(biāo)函數(shù)下降得最大(Shaw 1998中也使用了這種啟發(fā)式方法)。然后,對所有插入客戶后形成的分支按照lower bound進(jìn)行排序,從lower bound低的分支開始繼續(xù)往下分支(可以算是一種加速的策略)。同樣,請注意,該算法僅探索其lower bound比upper bound更好的分支。
3.2 bound
開始之前大家想想bound的難點在哪里呢?首先想想bound中最重要的兩個界:upper bound和lower bound:
- lower bound是指搜索過程中一個partial solution(比如上圖插入后形成的3個)的目標(biāo)值,因為并不能算完整的一個解,繼續(xù)往下的時候只可能增加(最小化問題)或者減少(最大化問題),因此它的意思是說當(dāng)前支路的最終形成解的目標(biāo)值下界(最終目標(biāo)值不可能比這個lower bound更好)。
- upper bound是指搜索過程中找到的一個feasible solution(比如上圖插入后形成的12個中滿足所有約束的就是)的目標(biāo)值,如果存在某支路的lower bound比upper bound還要差,那么該支路顯然是沒有繼續(xù)往下的必要了,可以剪去。
顯然可以使用LNS在destroy之前的解的目標(biāo)值作為upper bound,因為我們總是期望找到比當(dāng)前解更好的解,才會去進(jìn)行destroy和repair。現(xiàn)在的問題是如何對一個的lower bound應(yīng)該怎樣計算。下面講講幾種思路:
(1) 文獻(xiàn)中給出的思路,利用最小生成樹:


這個方案我試了,但是找到的lower bound實在是太低了,這個lower bound只考慮了距離因素,但問題中往往還存在時間窗等約束。因此這個方法在我當(dāng)時做的問題中只能說聊勝于無。
(2) 按照greedy的方法將所有未插入的Customer插入到他們最好的位置上,形成一個,然后該的目標(biāo)值作為lower bound。
但是這個lower bound是有缺陷的,因為很難保證不會錯過某些比較有潛力的分支。
(3) 直接利用當(dāng)前的的目標(biāo)值作為lower bound,也比較合理。但是該值往往太低了,這可能會導(dǎo)致要遍歷更多的分支,消耗更多時間。
以上就是一些思路,至于有沒有更好的bound方法,我后面也沒有往下深究了。當(dāng)時實現(xiàn)出來以后效果是有的,就是時間太長了,然后也放棄了。
當(dāng)然這篇paper后面也給了一個利用LDS進(jìn)行搜索以加快算法的速度,這里就不展開了,有空再說。感興趣的小伙伴可以去看看原paper,我會放到留言區(qū)的。
四、代碼環(huán)節(jié)代碼實現(xiàn)放兩個,一個是我當(dāng)時寫的一個DFSEXPLORER,采用的是思路2作為bound的,(代碼僅僅提供思路)如下:
private?void?DFSEXPLORER5(LNSSolution?node,?LNSSolution?upperBound,?int?dep)?{
??Queue?queue?=?new?LinkedList();
??LNSSolution?s_c_?=?node;
????????queue.add(s_c_);
????????int?es?=?1;
????????while?(!queue.isEmpty())?{
?????????s_c_?=?queue.remove();
????????????//v是一個完整的解
?????????if(s_c_.removalCustomers.isEmpty())?{
???????if(s_c_.cost?0.001)?{
????????//System.out.println("new?found?>?"+s_c_.cost+"?feasible?=?"+s_c_.feasible());
????????upperBound.cost?=?s_c_.cost;
????????upperBound.routes?=?s_c_.routes;
???????}
??????}else?{
???????
???????//System.out.println("l?>?"+s_c_.removalCustomers.size()?+?"?cost?=?"+s_c_.cost);
???????
???????double?minIDelta?=?Double.POSITIVE_INFINITY;
???????int?minIndex?=?-1;
???????Customer?c=null;
???????for(int?i?=?0;?i?????????Customer?cu?=?s_c_.removalCustomers.get(i);
????????double?d1?=?s_c_.minInsertionDeltas[cu.getCustomerNo()];
????????if(minIDelta?>?d1)?{
?????????minIDelta?=?d1;
?????????c?=?cu;
?????????minIndex?=?i;
????????}
???????}
???????ArrayList?neighborI_c?=?new?ArrayList();
???????for(?int?i?=?0;?i?????????Route?route?=?s_c_.routes[i];
???????????if(!MyUtil.checkCompatibility(c,?route.getAssignedVehicle()))?{
????????????continue;
???????????}
??????????????for?(int?j?=?0;?j?<=?route.getCustomersLength();?j++)?{
???????????????LNSSolution?s_i?=?s_c_.solClones();
???????????????s_i.insertCustomer(s_i.routes[i],?s_i.removalCustomers.get(minIndex),?j,?minIndex);
???????????????//updateIDAfterOneInserted(s_i,?s_i.routes[i]);
???????????????//s_i.calcLowerBound();
???????????????
???????????????double?o_c?=?s_i.lb;
???????????????updateInsertionDelta(s_i);
?????????double?n_c?=?s_i.lb;
?????????//if(o_c?!=?n_c)System.out.println("o?=?"+o_c+"?n?=?"+n_c);
???????????????
???????????????neighborI_c.add(s_i);
??????????????}
??????????}
???????Collections.sort(neighborI_c);
???????
???????for(LNSSolution?s:neighborI_c)?{
????????//System.out.println("lBound?"+s.lb+"?upperBound?=?"+upperBound.cost);
????????//updateInsertionDelta(s);
?????//s.calcLowerBound();
????????if(s.lb?/*&&?dep?>?0*/)?{
?????????//System.out.println("lBound?"+s.lb+"?upperBound?=?"+upperBound.cost);
?????????
?????????//System.out.println(s.removalCustomers.size());
?????????queue.add(s);
?????????es++;
?????????dep--;
????????}
???????}?
??????}
????????}
????????//System.out.println(es);
????}
第二個是GitHub上找到的一個人復(fù)現(xiàn)的,我已經(jīng)fork到我的倉庫中了:
https://github.com/dengfaheng/vrp
這個思路bound的思路呢沒有按照paper中的,應(yīng)該還是用的貪心進(jìn)行bound。看起來在R和RC系列的算例中效果其實也一般般,因為用了LDS吧可能。下面是運行的c1_2_1的截圖:
導(dǎo)入idea或者eclipse后等他安裝完依賴,運行下面的文件即可,更改算例的位置如圖所示:
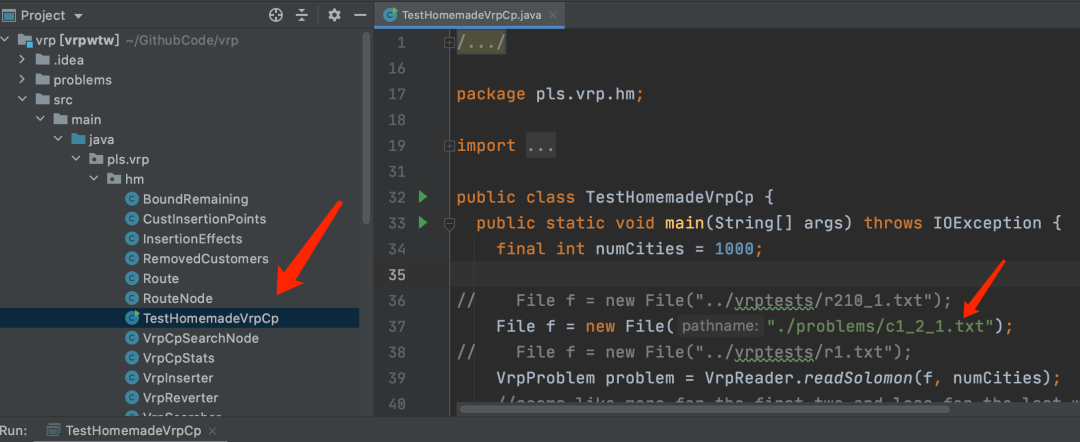
這個思路是直到借鑒的,大家在用LNS的時候也可以想想有什么更好的bound方法。
好了,這就是今天的分享了。可能有很多地方?jīng)]寫的很明白,因為涉及的點太多了我也只能講個大概提供一個思路而已。大家來了就幫我點個在看再走吧~
推薦閱讀:
干貨 | 想學(xué)習(xí)優(yōu)化算法,不知從何學(xué)起?
干貨 | 運籌學(xué)從何學(xué)起?如何快速入門運籌學(xué)算法?
干貨 | 學(xué)習(xí)算法,你需要掌握這些編程基礎(chǔ)(包含JAVA和C++)
干貨 | 算法學(xué)習(xí)必備訣竅:算法可視化解密
干貨 | 模擬退火、禁忌搜索、迭代局部搜索求解TSP問題Python代碼分享記得點個在看支持下哦~

