背景

關(guān)于濾波

首先援引來(lái)自知乎大神的解釋。

“一位專(zhuān)業(yè)課的教授給我們上課的時(shí)候，曾談到：filtering is weighting（濾波即加權(quán)）。濾波的作用就是給不同的信號(hào)分量不同的權(quán)重。最簡(jiǎn)單的loss pass filter， 就是直接把低頻的信號(hào)給1權(quán)重，而給高頻部分0權(quán)重。對(duì)于更復(fù)雜的濾波，比如維納濾波, 則要根據(jù)信號(hào)的統(tǒng)計(jì)知識(shí)來(lái)設(shè)計(jì)權(quán)重。

從統(tǒng)計(jì)信號(hào)處理的角度，降噪可以看成濾波的一種。降噪的目的在于突出信號(hào)本身而抑制噪聲影響。從這個(gè)角度，降噪就是給信號(hào)一個(gè)高的權(quán)重而給噪聲一個(gè)低的權(quán)重。維納濾波就是一個(gè)典型的降噪濾波器。”

關(guān)于卡爾曼濾波

Kalman Filter 算法，是一種遞推預(yù)測(cè)濾波算法，算法中涉及到濾波，也涉及到對(duì)下一時(shí)刻數(shù)據(jù)的預(yù)測(cè)。Kalman Filter 由一系列遞歸數(shù)學(xué)公式描述。它提供了一種高效可計(jì)算的方法來(lái)估計(jì)過(guò)程的狀態(tài)，并使估計(jì)均方誤差最小。卡爾曼濾波器應(yīng)用廣泛且功能強(qiáng)大：它可以估計(jì)信號(hào)的過(guò)去和當(dāng)前狀態(tài)，甚至能估計(jì)將來(lái)的狀態(tài)，即使并不知道模型的確切性質(zhì)。

Kalman Filter 也可以被認(rèn)為是一種數(shù)據(jù)融合算法（Data fusion algorithm），已有50多年的歷史，是當(dāng)今使用最重要和最常見(jiàn)的數(shù)據(jù)融合算法之一。Kalman Filter 的巨大成功歸功于其小的計(jì)算需求，優(yōu)雅的遞歸屬性以及作為具有高斯誤差統(tǒng)計(jì)的一維線性系統(tǒng)的最優(yōu)估計(jì)器的狀態(tài)。

Kalman Filter 只能減小均值為0的測(cè)量噪聲帶來(lái)的影響。只要噪聲期望為0，那么不管方差多大，只要迭代次數(shù)足夠多，那效果都很好。反之，噪聲期望不為0，那么估計(jì)值就還是與實(shí)際值有偏差[3]。

問(wèn)題描述

上面的描述可能把大家繞暈了，下面來(lái)點(diǎn)輕松的。

我們會(huì)有一個(gè)疑問(wèn)：卡爾曼濾波到底是如何解決實(shí)際問(wèn)題的呢？

我們以機(jī)器人為例介紹卡爾曼濾波的原理，我們的任務(wù)是要預(yù)測(cè)機(jī)器人的狀態(tài)，包括位置與速度，即可表示為：

某個(gè)時(shí)刻，我們不知道真實(shí)的位置與速度到底是多少，二者存在一個(gè)所有可能性的組合，大致如下圖所示。

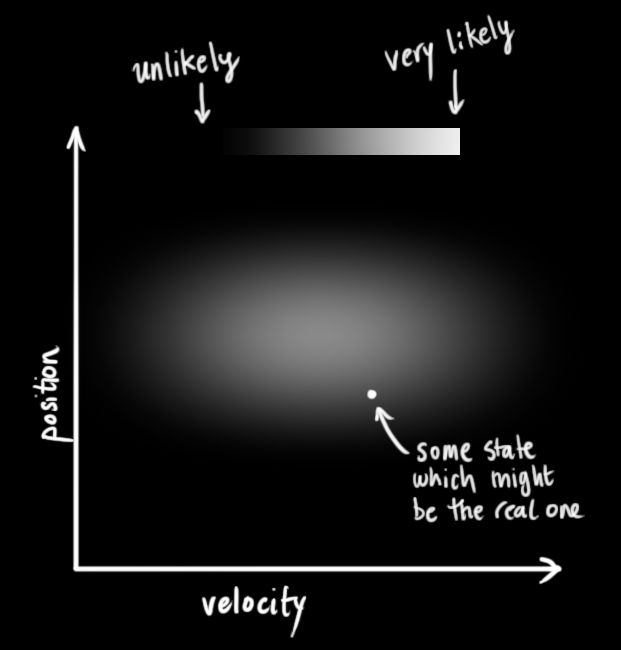
卡爾曼濾波假設(shè)狀態(tài)所有的變量都是隨機(jī)的且都服從高斯分布，每個(gè)變量都有其對(duì)應(yīng)的均值以及方差（它代表了不確定性）。

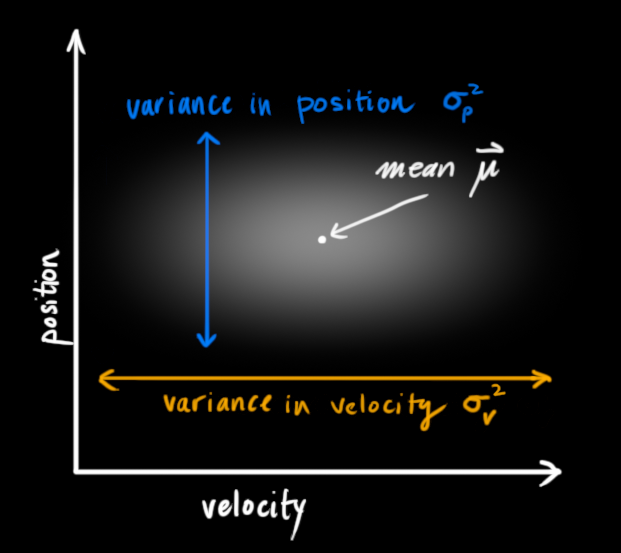
在上圖中，位置和速度是不相關(guān)（uncorrelated）的，這意味著某個(gè)變量的狀態(tài)不會(huì)告訴你其他變量的狀態(tài)是怎樣的。即，我們雖然知道現(xiàn)在的速度，但無(wú)法從現(xiàn)在的速度推測(cè)出現(xiàn)在的位置。但實(shí)際上并非如此，我們知道速度和位置是有關(guān)系的（correlated），這樣一來(lái)二者之間的組合關(guān)系變成了如下圖所示的情況。

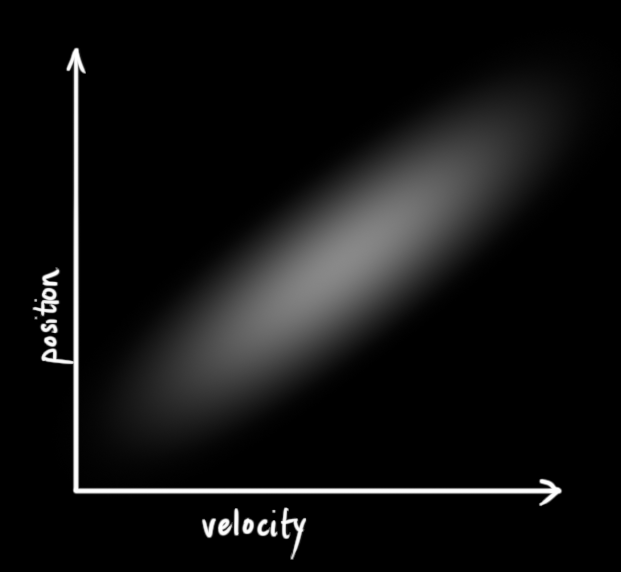
這種情況是很容易發(fā)生的，例如，如果速度很快，我們可能會(huì)走得更遠(yuǎn)，所以我們的位置會(huì)更大。如果我們走得很慢，我們就不會(huì)走得太遠(yuǎn)。

這種狀態(tài)變量之間的關(guān)系很重要，因?yàn)樗梢詾槲覀兲峁?strong>更多信息：One measurement tells us something about what the others could be。這就是卡爾曼濾波器的目標(biāo)，我們希望從不確定的測(cè)量中盡可能多地獲取信息！

這種狀態(tài)量的相關(guān)性可以由協(xié)方差矩陣表示。簡(jiǎn)而言之，矩陣的每個(gè)元素是第i個(gè)狀態(tài)變量和第j個(gè)狀態(tài)變量之間的相關(guān)度。（顯然地可以知道協(xié)方差矩陣是對(duì)稱(chēng)的，這意味著交換i和j都沒(méi)關(guān)系）。協(xié)方差矩陣通常標(biāo)記為“?”，因此我們將它們的元素稱(chēng)為“”。

狀態(tài)預(yù)測(cè)

問(wèn)題的矩陣形式表示

我們把狀態(tài)建模成高斯分布（Gaussian blob，由于二維高斯分布長(zhǎng)得像一個(gè)個(gè)小泡泡，之所以長(zhǎng)這個(gè)樣子，可參考鏈接[2]）。我們需要求解/估計(jì)在時(shí)間時(shí)刻的兩個(gè)信息：1. 最優(yōu)估計(jì)以及它的協(xié)方差矩陣，我們可以寫(xiě)成下面矩陣形式：

（當(dāng)然，這里我們僅使用位置和速度，但是請(qǐng)記住狀態(tài)可以包含任意數(shù)量的變量，并且可以表示所需的任何變量）

接下來(lái)，我們需要某種方式來(lái)查看當(dāng)前狀態(tài)（時(shí)刻）并預(yù)測(cè)在時(shí)刻處的狀態(tài)。請(qǐng)記住，我們不知道哪個(gè)狀態(tài)是“真實(shí)”狀態(tài)，但是這里提到的預(yù)測(cè)（prediction）并不在乎這些。

我們可以用一個(gè)矩陣來(lái)表示這個(gè)預(yù)測(cè)過(guò)程：

這個(gè)矩陣將原始估計(jì)中的每個(gè)點(diǎn)移動(dòng)到新的預(yù)測(cè)位置。

那么問(wèn)題來(lái)了，應(yīng)該如何使用上述矩陣來(lái)預(yù)測(cè)下一時(shí)刻的位置和速度呢？為了闡述這個(gè)過(guò)程，我們使用了一個(gè)非常基礎(chǔ)的運(yùn)動(dòng)學(xué)公式（初中物理中就學(xué)過(guò)）進(jìn)行描述：

寫(xiě)成矩陣形式：

現(xiàn)在我們有了一個(gè)預(yù)測(cè)矩陣或者叫做狀態(tài)轉(zhuǎn)移矩陣，該矩陣可以幫助我們計(jì)算下一個(gè)時(shí)刻的狀態(tài)。但我們?nèi)匀徊恢廊绾胃聽(tīng)顟B(tài)的協(xié)方差矩陣，其實(shí)過(guò)程也是很簡(jiǎn)單，如果我們將分布中的每個(gè)點(diǎn)乘以矩陣，那么其協(xié)方差矩陣會(huì)發(fā)生什么？

將公式(3)代入公式(4)我們可以得到：

External influence

不過(guò)我們并沒(méi)有考慮到所有的影響因素。可能有一些與狀態(tài)本身無(wú)關(guān)的變化——如外界因素可能正在影響系統(tǒng)。

例如，我們用狀態(tài)對(duì)列車(chē)的運(yùn)動(dòng)進(jìn)行建模，如果列車(chē)長(zhǎng)加大油門(mén)，火車(chē)就加速。同樣，在我們的機(jī)器人示例中，導(dǎo)航系統(tǒng)軟件可能會(huì)發(fā)出使車(chē)輪轉(zhuǎn)動(dòng)或停止的命令。如果我們很明確地知道這些因素，我們可以將其放在一起構(gòu)成一個(gè)向量，我們可以對(duì)這個(gè)量進(jìn)行某些“處理”，然后將其添加到我們的預(yù)測(cè)中對(duì)狀態(tài)進(jìn)行更正。

假設(shè)我們知道由于油門(mén)設(shè)置或控制命令而產(chǎn)生的預(yù)期加速度。根據(jù)基本運(yùn)動(dòng)學(xué)原理，我們可以得到下式：

將其寫(xiě)成矩陣形式：

其中被稱(chēng)為控制矩陣，被稱(chēng)為控制向量。（注意：對(duì)于沒(méi)有外部影響的簡(jiǎn)單系統(tǒng)，可以忽略這個(gè)控制項(xiàng)）。

如果我們的預(yù)測(cè)并不是100％準(zhǔn)確模型，這會(huì)發(fā)生什么呢？

External uncertainty

如果狀態(tài)僅僅依賴(lài)其自身的屬性進(jìn)行演進(jìn)，那一切都會(huì)很好。如果狀態(tài)受到外部因素進(jìn)行演進(jìn)，我們只要知道這些外部因素是什么，那么一切仍然很好。

但在實(shí)際使用中，我們有時(shí)不知道的這些外部因素到底是如何被建模的。例如，我們要跟蹤四軸飛行器，它可能會(huì)隨風(fēng)搖晃；如果我們跟蹤的是輪式機(jī)器人，則車(chē)輪可能會(huì)打滑，或者因地面顛簸導(dǎo)致其減速。我們無(wú)法跟蹤這些外部因素，如果發(fā)生任何這些情況，我們的預(yù)測(cè)可能會(huì)出錯(cuò)，因?yàn)槲覀儾](méi)有考慮這些因素。

通過(guò)在每個(gè)預(yù)測(cè)步驟之后添加一些新的不確定性，我們可以對(duì)與“世界”相關(guān)的不確定性進(jìn)行建模（如我們無(wú)法跟蹤的事物）：

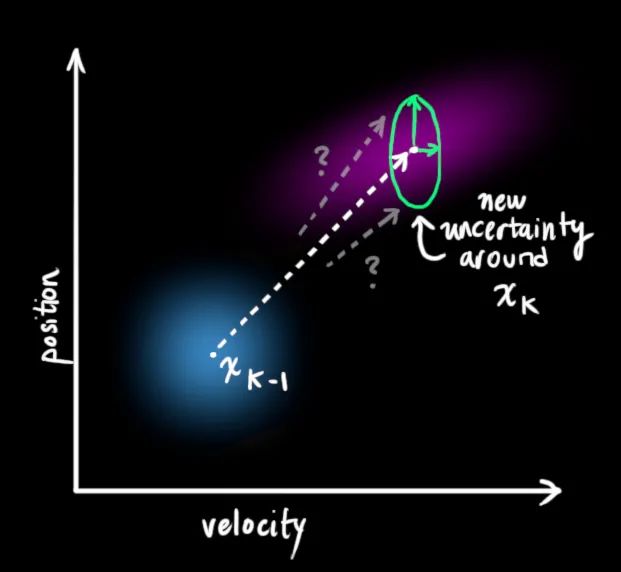
這樣一來(lái)，由于新增的不確定性原始估計(jì)中的每個(gè)狀態(tài)都可能遷移到多個(gè)狀態(tài)。因?yàn)槲覀兎浅Ｏ矚g用高斯分布進(jìn)行建模，此處也不例外。我們可以說(shuō)的每個(gè)點(diǎn)都移動(dòng)到具有協(xié)方差的高斯分布內(nèi)的某個(gè)位置，如下圖所示：

這將產(chǎn)生一個(gè)新的高斯分布，其協(xié)方差不同（但均值相同）：

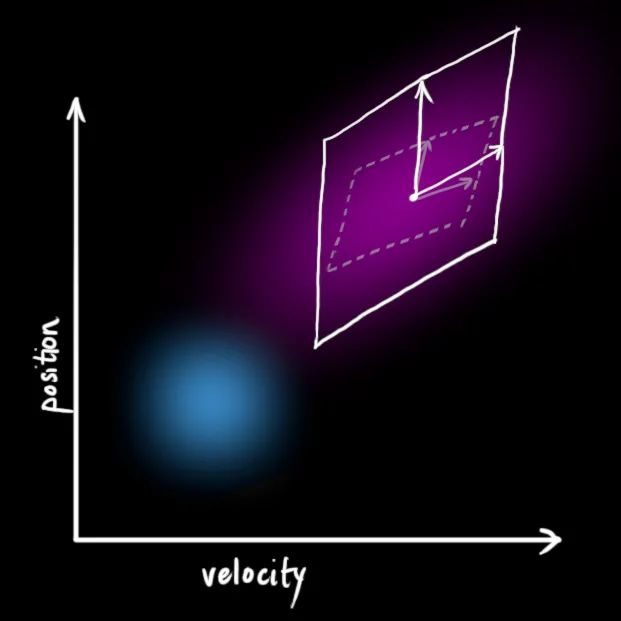
所以呢，我們?cè)跔顟B(tài)量的協(xié)方差中增加額外的協(xié)方差，所以預(yù)測(cè)階段完整的狀態(tài)轉(zhuǎn)移方程為：

換句話說(shuō)：新的最佳估計(jì)是根據(jù)先前的最佳估計(jì)做出的預(yù)測(cè)，再加上對(duì)已知外部影響的校正。

新的不確定度是根據(jù)先前的不確定度做出的預(yù)測(cè)，再加上來(lái)自環(huán)境額外的不確定度。

上述過(guò)程描繪了狀態(tài)預(yù)測(cè)過(guò)程，那么當(dāng)我們從傳感器中獲取一些測(cè)量數(shù)據(jù)時(shí)會(huì)發(fā)生什么呢？

狀態(tài)更新

利用測(cè)量進(jìn)一步修正狀態(tài)

假設(shè)我們有幾個(gè)傳感器，這些傳感器可以向我們提供有關(guān)系統(tǒng)狀態(tài)的信息。就目前而言，測(cè)量什么量都無(wú)關(guān)緊要，也許一個(gè)讀取位置，另一個(gè)讀取速度。每個(gè)傳感器都告訴我們有關(guān)狀態(tài)的一些間接信息（換句話說(shuō)，傳感器在狀態(tài)下運(yùn)作并產(chǎn)生一組測(cè)量讀數(shù)）。

請(qǐng)注意，測(cè)量的單位可能與狀態(tài)量的單位不同。我們使用矩陣對(duì)傳感器的測(cè)量進(jìn)行建模。

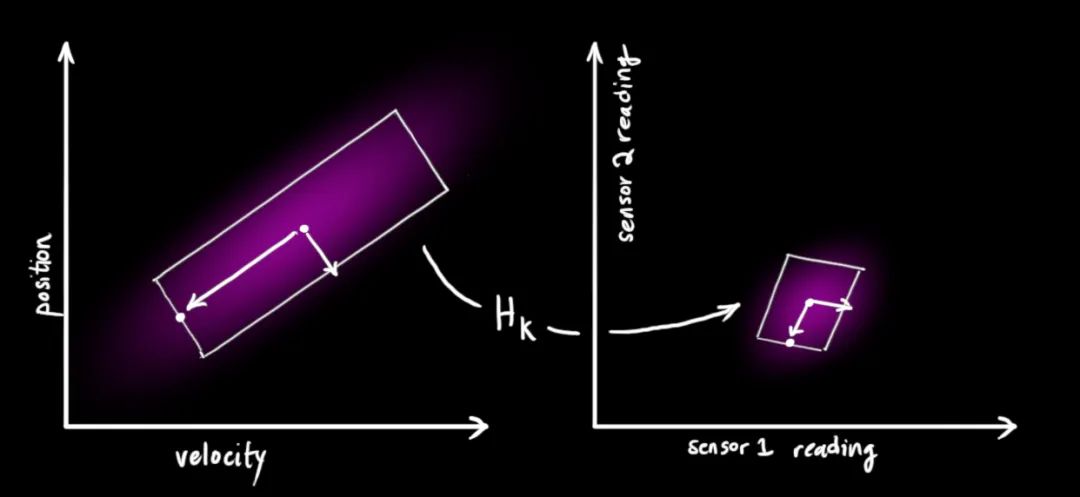
所以我們期望傳感器的度數(shù)可以被建模成如下形式：

卡爾曼濾波器的偉大之處就在于它能夠處理傳感器噪聲。換句話說(shuō)，傳感器本身的測(cè)量是不準(zhǔn)確的，且原始估計(jì)中的每個(gè)狀態(tài)都可能導(dǎo)致一定范圍的傳感器讀數(shù)，而卡爾曼濾波能夠在這些不確定性存在的情況下找到最優(yōu)的狀態(tài)。

根據(jù)傳感器的讀數(shù)，我們會(huì)猜測(cè)系統(tǒng)正處于某個(gè)特定狀態(tài)。但是由于不確定性的存在，某些狀態(tài)比其他狀態(tài)更可能產(chǎn)生我們看到的讀數(shù)：

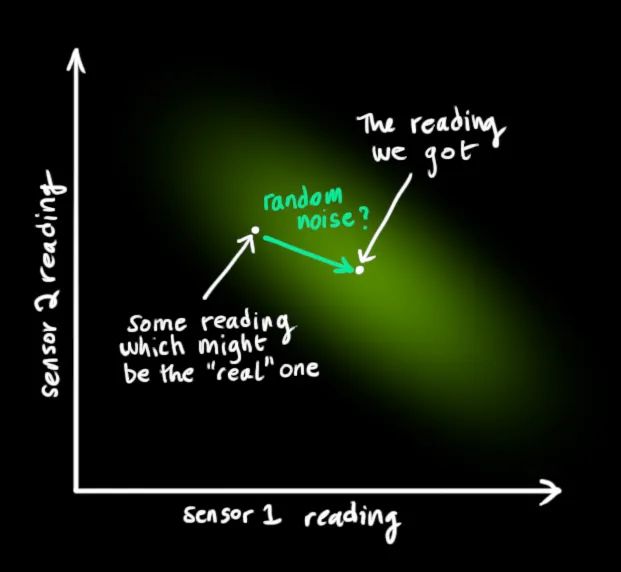
我們將這種不確定性（如傳感器噪聲）的協(xié)方差表示為，讀數(shù)的分布均值等于我們觀察到傳感器的讀數(shù)，我們將其表示為

這樣一來(lái)，我們有了兩個(gè)高斯分布：一個(gè)圍繞通過(guò)狀態(tài)轉(zhuǎn)移預(yù)測(cè)的平均值，另一個(gè)圍繞實(shí)際傳感器讀數(shù)。

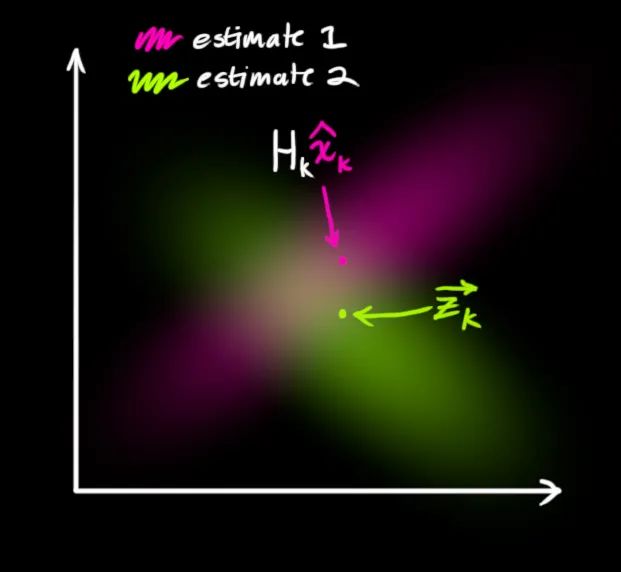
因此，我們需要將基于預(yù)測(cè)狀態(tài)（粉紅色）的推測(cè)讀數(shù)與基于實(shí)際觀察到的傳感器讀數(shù)（綠色）進(jìn)行融合。

那么融合后最有可能的新?tīng)顟B(tài)是什么？對(duì)于任何可能的讀數(shù)，我們都有兩個(gè)相關(guān)的概率：（1）我們的傳感器讀數(shù)是的測(cè)量值的概率，以及（2）先前估計(jì)值的概率認(rèn)為是我們應(yīng)該看到的讀數(shù)。

如果我們有兩個(gè)概率，并且想知道兩個(gè)概率都為真的機(jī)會(huì)，則將它們相乘。因此，我們對(duì)兩個(gè)高斯分布進(jìn)行了相乘處理：

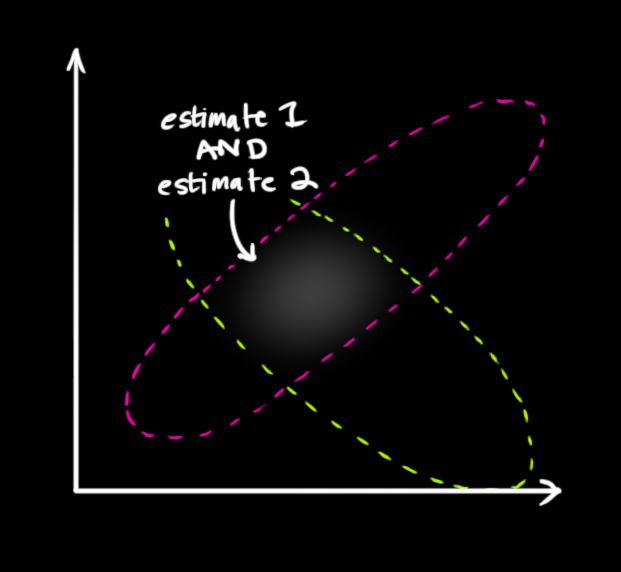
兩個(gè)概率分布相乘得到的就是上圖中的重疊部分。而且重疊部分的概率分布會(huì)比我們之前的任何一個(gè)估計(jì)值/讀數(shù)都精確得多，這個(gè)分布的均值就是兩種估計(jì)最有可能配置（得到的狀態(tài)）。

事實(shí)證明，兩個(gè)獨(dú)立的高斯分布相乘之后會(huì)得到一個(gè)新的具有其均值和協(xié)方差矩陣的高斯分布！下面開(kāi)始推公式。

合并兩個(gè)高斯分布

首先考慮一維高斯情況：一個(gè)均值為，方差為的高斯分布的形式為：

我們想知道將兩個(gè)高斯曲線相乘會(huì)發(fā)生什么。下圖中的藍(lán)色曲線表示兩個(gè)高斯總體的（未歸一化）交集：

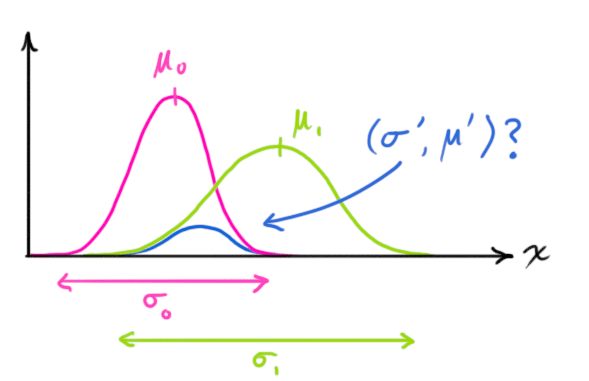
將公式(9)代入公式(10)，我們可以得到新的高斯分布的均值和方差如下所示：

我們將其中的一小部分重寫(xiě)為：

這樣一來(lái)，公式的形式就簡(jiǎn)單多了！我們順勢(shì)將公式(12)和(13)的矩陣形式寫(xiě)在下面：

其中表示新高斯分布的協(xié)方差矩陣，是每個(gè)維度的均值，就是大名鼎鼎的“卡爾曼增益”（Kalman gain）。

公式匯總

我們有兩個(gè)高斯分布，一個(gè)是我們預(yù)測(cè)的觀測(cè)，另外一個(gè)是實(shí)際的觀測(cè)(傳感器讀數(shù))，我們將這兩個(gè)高斯分布帶入公式(15)中就可以得到二者的重疊區(qū)域：

從公式(14)我們可以知道，卡爾曼增益是：

然后我們將公式(16)與公式(17)中的去除，同時(shí)將后面的去除，我們可以得到最終的化簡(jiǎn)形式的更新方程：

圖說(shuō)

大功告成，就是更新后的最優(yōu)狀態(tài)！接下來(lái)我們可以繼續(xù)進(jìn)行預(yù)測(cè)，然后更新，重復(fù)上述過(guò)程！下圖給出卡爾曼濾波信息流。

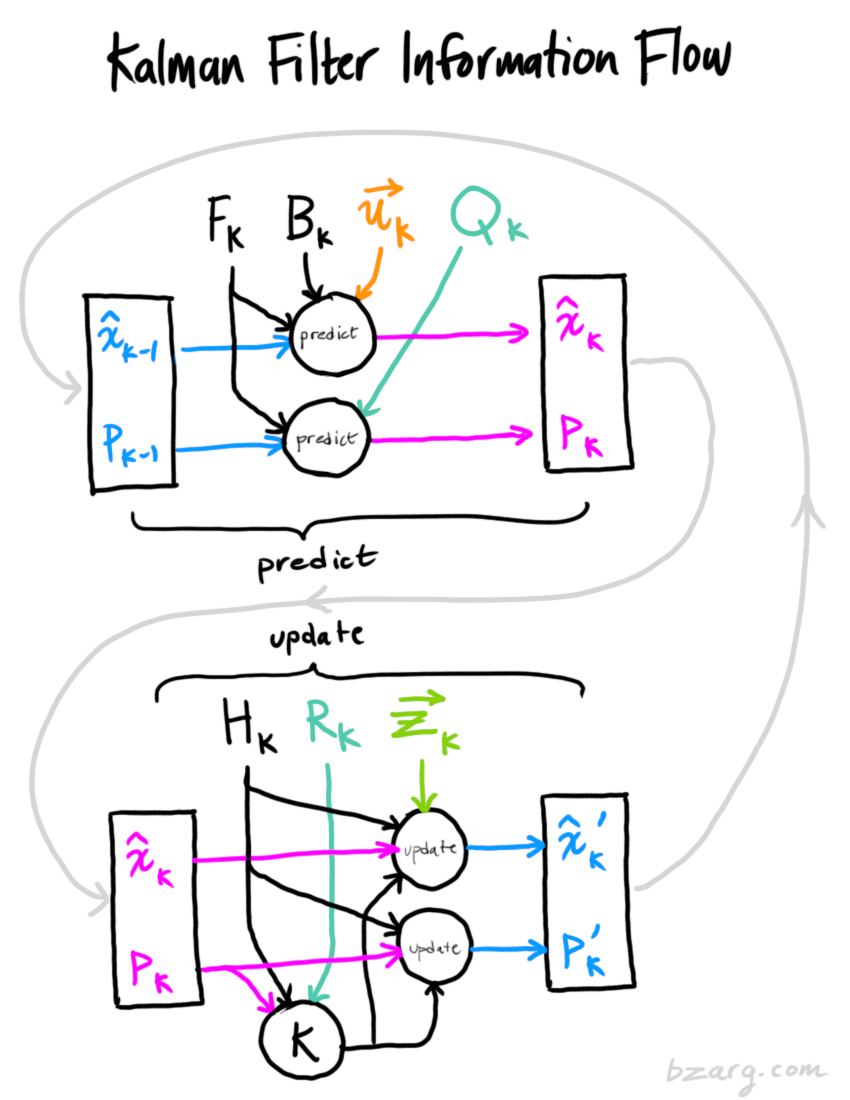
總結(jié)

在上述所有數(shù)學(xué)公式中，你需要實(shí)現(xiàn)的只是公式(7)(18)和(19)。（或者，如果你忘記了這些，可以從等式(4)和(15)重新推導(dǎo)所有內(nèi)容。）

這將使你能夠準(zhǔn)確地對(duì)任何線性系統(tǒng)建模。對(duì)于非線性系統(tǒng)，我們使用擴(kuò)展卡爾曼濾波器，該濾波器通過(guò)簡(jiǎn)單地線性化預(yù)測(cè)和測(cè)量值的均值進(jìn)行工作。

參考資料

交流群

歡迎加入公眾號(hào)讀者群一起和同行交流，目前有SLAM、三維視覺(jué)、傳感器、自動(dòng)駕駛、計(jì)算攝影、檢測(cè)、分割、識(shí)別、醫(yī)學(xué)影像、GAN、算法競(jìng)賽等微信群（以后會(huì)逐漸細(xì)分），請(qǐng)掃描下面微信號(hào)加群，備注：”昵稱(chēng)+學(xué)校/公司+研究方向“，例如：”張三?+?上海交大?+?視覺(jué)SLAM“。請(qǐng)按照格式備注，否則不予通過(guò)。添加成功后會(huì)根據(jù)研究方向邀請(qǐng)進(jìn)入相關(guān)微信群。請(qǐng)勿在群內(nèi)發(fā)送廣告，否則會(huì)請(qǐng)出群，謝謝理解~