或許是一本可以徹底改變你刷 LeetCode 效率的題解書
經(jīng)過了半年時間打磨,投入諸多人力,這本 LeetCode 題解書終于要和大家見面了。
背景
自 LeetCode 題解 (現(xiàn)在已經(jīng)接近 45k star 了)項目被大家開始關(guān)注,就有不少出版社開始聯(lián)系我寫書。剛開始后的時候,我并沒有這個打算,覺得寫這個相對于博客形式的題解要耗費時間,且并不一定效果比博客形式的效果好。后來當(dāng)我向大家提及“出版社找我寫書”這件事情的時候,很多人表示“想要買書,于是我就開始打算寫這樣一本書。但是一個完全沒有寫書經(jīng)驗的人,獨立完成一本書工作量還是蠻大的,因此我打算尋求其他志同道合人士的幫助。
團(tuán)隊介紹
團(tuán)隊成員大都來自 985, 211 學(xué)校計算機(jī)系,大家經(jīng)常參加算法競賽,也堅持參加 LeetCode 周賽。在這個過程中,我們積累了很多經(jīng)驗,希望將這些經(jīng)驗分享給大家,以減少大家在刷題過程中的阻礙,讓大家更有效率的刷題。本書尤其適合那些剛剛開始刷題的人,如果你剛開始刷題,或者刷了很多題面對新題還是無法很好的解決,那么這本書肯定很適合你。最后歡迎大家加入我們的讀者群和作者進(jìn)行交流。
讀者群會在新書出版之后的第一時間開放。
作者 - lucifer 作者 - BY 作者 - fanlu 作者 - hlxing 作者 - lazybing
樣張
這里給大家開放部分章節(jié)內(nèi)容給大家,讓大家嘗嘗鮮。
我們開放了第八章第五小節(jié)給大家看,以下是具體內(nèi)容:
8.5 1206. 設(shè)計跳表
題目描述
不使用任何庫函數(shù),設(shè)計一個跳表。
跳表是在
時間內(nèi)完成增加、刪除、搜索操作的數(shù)據(jù)結(jié)構(gòu)。跳表相比于樹堆與紅黑樹,其功能與性能相當(dāng),并且跳表的代碼長度相較下更短,其設(shè)計思想與鏈表相似。
跳表中有很多層,每一層是一個短的鏈表。在第一層的作用下,增加、刪除和搜索操作的時間復(fù)雜度不超過
。跳表的每一個操作的平均時間復(fù)雜度是 ,空間復(fù)雜度是
。
在本題中,你的設(shè)計應(yīng)該要包含這些函數(shù):
bool search(int target) : 返回 target 是否存在于跳表中。 void add(int num): 插入一個元素到跳表。 bool erase(int num): 在跳表中刪除一個值,如果 num 不存在,直接返回 false. 如果存在多個 num ,刪除其中任意一個即可。
注意,跳表中可能存在多個相同的值,你的代碼需要處理這種情況。
樣例:
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // 返回 false
skiplist.add(4);
skiplist.search(1); // 返回 true
skiplist.erase(0); // 返回 false,0 不在跳表中
skiplist.erase(1); // 返回 true
skiplist.search(1); // 返回 false,1 已被擦除
約束條件:0 <= num, target <= 20000最多調(diào)用 50000 次 search, add, 以及 erase 操作。
思路
首先,使用跳表會將數(shù)據(jù)存儲成有序的。在數(shù)據(jù)結(jié)構(gòu)當(dāng)中,我們通常有兩種基本的線性結(jié)構(gòu),結(jié)合有序數(shù)據(jù),表達(dá)如下:
有序鏈表,我們有三種基本操作: 查找指定的數(shù)據(jù):時間復(fù)雜度為
,
為數(shù)據(jù)位于鏈表的位置。 插入指定的數(shù)據(jù):時間復(fù)雜度為 ,
為數(shù)據(jù)位于鏈表的位置。因為插入數(shù)據(jù)之前,需要先查找到可以插入的位置。 刪除指定的數(shù)據(jù):時間復(fù)雜度為 ,
為數(shù)據(jù)位于鏈表的位置。因為刪除數(shù)據(jù)之前,需要先查找到可以插入的位置。 有序數(shù)組: 查找指定的數(shù)據(jù):如果使用二分查找,時間復(fù)雜度為 ,
為數(shù)據(jù)的個數(shù)。 插入指定的數(shù)據(jù):時間復(fù)雜度為 , 因為數(shù)組是順序存儲,插入新的數(shù)據(jù)時,我們需要向后移動指定位置后面的數(shù)據(jù),這里
為數(shù)據(jù)的個數(shù)。 刪除指定的數(shù)據(jù):時間復(fù)雜度為 , 因為數(shù)組是順序存儲,刪除數(shù)據(jù)時,我們需要向前移動指定位置后面的數(shù)據(jù),這里
為數(shù)據(jù)的個數(shù)。 。那么如何來提高鏈表的查詢效率呢?如下圖所示,我們可以從原始鏈表中每兩個元素抽出來一個元素,加上一級索引,并且一級索引指向原始鏈表:
如果我們想要查找 9 ,在原始鏈表中查找路徑是
, 而在添加了一級索引的查找路徑是
,很明顯,查找效率提升了。按照這樣的思路,我們在第 1 級索引上再加第 2 級索引,再加第 3 級索引,以此類推,這樣在數(shù)據(jù)量非常大的時候,使得我們查找數(shù)據(jù)的時間復(fù)雜度為
退化為
方案 1:每次插入數(shù)據(jù)后,將跳表的索引全部刪除后重建,我們知道索引的結(jié)點個數(shù)為 (在空間復(fù)雜度分析時會有明確的數(shù)學(xué)推導(dǎo)),那么每次重建索引,重建的時間復(fù)雜度至少是
級別,很明顯不可取。 方案 2:通過隨機(jī)性來維護(hù)索引。假設(shè)跳表的每一層的提升概率為 ,最理想的情況就是每兩個元素提升一個元素做索引。而通常意義上,只要元素的數(shù)量足夠多,且抽取足夠隨機(jī)的話,我們得到的索引將會是比較均勻的。盡管不是每兩個抽取一個,但是對于查找效率來講,影響并不很大。我們要知道,設(shè)計良好的數(shù)據(jù)結(jié)構(gòu)往往都是用來應(yīng)對大數(shù)據(jù)量的場景的。因此,我們這樣維護(hù)索引:
隨機(jī)抽取 個元素作為 1 級索引,隨機(jī)抽取 作為 2 級索引,以此類推,一直到最頂層索引。 的概率建立一級索引、
的概率建立二級索引、
randomLevel() 方法返回 1 表示當(dāng)前插入的元素不需要建立索引,只需要存儲數(shù)據(jù)到原始鏈表即可(概率 1/2) randomLevel() 方法返回 2 表示當(dāng)前插入的元素需要建立一級索引(概率 1/4) randomLevel() 方法返回 3 表示當(dāng)前插入的元素需要建立二級索引(概率 1/8) randomLevel() 方法返回 4 表示當(dāng)前插入的元素需要建立三級索引(概率 1/16) ...... , 這樣是不是有問題呢?實際上,只要
方法返回的數(shù)大于 1,我們都會建立一級索引,而返回值為 1 的概率是
。所以,建立一級索引的概率其實是
。同上,當(dāng)
方法返回值
時,我們會建立二級或二級以上的索引,都會在二級索引中添加元素。而在二級索引中添加元素的概率是
而神奇的跳表能夠在
時間內(nèi)完成增加、刪除、搜索操作。下面我們分別分析增加、刪除和搜索這 3 個三個基本操作。
跳表的查找
現(xiàn)在我們通過一個簡單的例子來描述跳表是如何實現(xiàn)的。假設(shè)我們有一個有序鏈表如下圖: 原始方法中,查找的時間復(fù)雜度為
原始方法中,查找的時間復(fù)雜度為
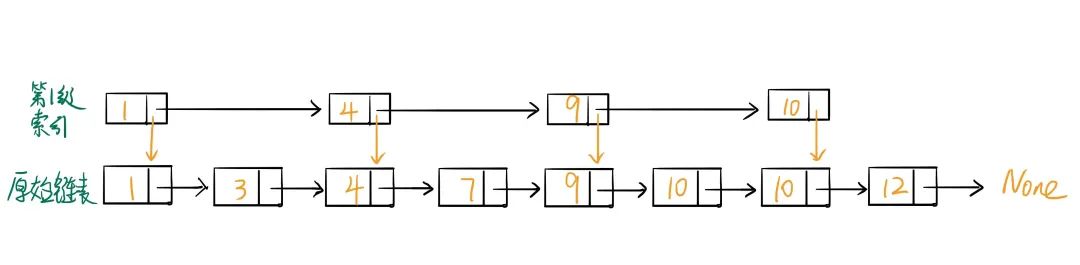
1->3->4->7->91->4->9。這就是跳表的思想,也就是我們通常所說的“空間換時間”。
跳表的插入
跳表插入數(shù)據(jù)看起來很簡單,我們需要保持?jǐn)?shù)據(jù)有序,因此,第一步我們需要像查找元素一樣,找到新元素應(yīng)該插入的位置,然后再插入。
但是這樣會存在一個問題,如果我們一直往原始鏈表中插入數(shù)據(jù),但是不更新索引,那么會導(dǎo)致兩個索引結(jié)點之間的數(shù)據(jù)非常多,在極端情況下,跳表會退化成單鏈表,從而導(dǎo)致查找效率由
。因此,我們需要在插入數(shù)據(jù)的同時,增加相應(yīng)的索引或者重建索引。
那么具體代碼該如何實現(xiàn),才能夠讓跳表在每次插入新元素時,盡量讓該元素有
的概率建立三級索引,以此類推。因此,我們需要一個概率算法。
在通常的跳表實現(xiàn)當(dāng)中,我們會設(shè)計一個 randomLevel() 方法,該方法會隨機(jī)生成 1~MAX_LEVEL 之間的數(shù) (MAX_LEVEL 表示索引的最高層數(shù))
可能有的同學(xué)會有疑問,我們需要一級索引中元素的個數(shù)時原始鏈表的一半,但是我們 randomLevel() 方法返回 2(建立一級索引)的概率是
randomLevel()randomLevel()>2。以此類推,我們推導(dǎo)出 randomLevel() 符合我們的設(shè)計要求。
下面我們通過仿照 redis zset.c 的 randomLevel 的代碼:
##
# 1. SKIPLIST_P 為提升的概率,本案例中我們設(shè)置為 1/2, 如果我們想要節(jié)省空間利用效率,可以適當(dāng)?shù)慕档驮撝担瑥亩鴾p少索引元素個數(shù)。在 redis 中 SKIPLIST_P 被設(shè)定為 0.25。
# 2. redis 中通過使用位運算來提升浮點數(shù)比較的效率,在本案例中被簡化
def randomLevel():
level = 1
while random() < SKIPLIST_P and level < MAX_LEVEL:
level += 1
return level
跳表的刪除
跳表的刪除相對來講稍微簡單一些。我們在刪除數(shù)據(jù)的同時,需要刪除對應(yīng)的索引結(jié)點。
代碼
from typing import Optional
import random
class ListNode:
def __init__(self, data: Optional[int] = None):
self._data = data # 鏈表結(jié)點的數(shù)據(jù)域,可以為空(目的是方便創(chuàng)建頭節(jié)點)
self._forwards = [] # 存儲各個索引層級中該結(jié)點的后驅(qū)索引結(jié)點
class Skiplist:
_MAX_LEVEL = 16 # 允許的最大索引高度,該值根據(jù)實際需求設(shè)置
def __init__(self):
self._level_count = 1 # 初始化當(dāng)前層級為 1
self._head = ListNode()
self._head._forwards = [None] * self._MAX_LEVEL
def search(self, target: int) -> bool:
p = self._head
for i in range(self._level_count - 1, -1, -1): # 從最高索引層級不斷搜索,如果當(dāng)前層級沒有,則下沉到低一級的層級
while p._forwards[i] and p._forwards[i]._data < target:
p = p._forwards[i]
if p._forwards[0] and p._forwards[0]._data == target:
return True
return False
def add(self, num: int) -> None:
level = self._random_level() # 隨機(jī)生成索引層級
if self._level_count < level: # 如果當(dāng)前層級小于 level, 則更新當(dāng)前最高層級
self._level_count = level
new_node = ListNode(num) # 生成新結(jié)點
new_node._forwards = [None] * level
update = [self._head] * self._level_count # 用來保存各個索引層級插入的位置,也就是新結(jié)點的前驅(qū)結(jié)點
p = self._head
for i in range(self._level_count - 1, -1, -1): # 整段代碼獲取新插入結(jié)點在各個索引層級的前驅(qū)節(jié)點,需要注意的是這里是使用的當(dāng)前最高層級來循環(huán)。
while p._forwards[i] and p._forwards[i]._data < num:
p = p._forwards[i]
update[i] = p
for i in range(level): # 更新需要更新的各個索引層級
new_node._forwards[i] = update[i]._forwards[i]
update[i]._forwards[i] = new_node
def erase(self, num: int) -> bool:
update = [None] * self._level_count
p = self._head
for i in range(self._level_count - 1, -1, -1):
while p._forwards[i] and p._forwards[i]._data < num:
p = p._forwards[i]
update[i] = p
if p._forwards[0] and p._forwards[0]._data == num:
for i in range(self._level_count - 1, -1, -1):
if update[i]._forwards[i] and update[i]._forwards[i]._data == num:
update[i]._forwards[i] = update[i]._forwards[i]._forwards[i]
return True
while self._level_count > 1 and not self._head._forwards[self._level_count]:
self._level_count -= 1
return False
def _random_level(self, p: float = 0.5) -> int:
level = 1
while random.random() < p and level < self._MAX_LEVEL:
level += 1
return level
復(fù)雜度分析
空間復(fù)雜度
跳表通過建立索引提高查找的效率,是典型的“空間換時間”的思想,那么空間復(fù)雜度到底是多少呢?我們假設(shè)原始鏈表有
個元素,一級索引有
,二級索引有
,k 級索引有
個元素,而最高級索引一般有
個元素。所以,索引結(jié)點的總和是
,因此可以得出空間復(fù)雜度是
,
是原始鏈表的長度。
上面的假設(shè)前提是每兩個結(jié)點抽出一個結(jié)點到上層索引。那么如果我們每三個結(jié)點抽出一個結(jié)點到上層索引,那么索引總和就是 , 額外空間減少了一半。因此我們可以通過減少索引的數(shù)量來減少空間復(fù)雜度,但是相應(yīng)的會帶來查找效率一定的下降。而具體這個閾值該如何選擇,則要看具體的應(yīng)用場景。
另外需要注意的是,在實際的應(yīng)用當(dāng)中,索引結(jié)點往往不需要存儲完整的對象,只需要存儲對象的 key 和對應(yīng)的指針即可。因此當(dāng)對象比索引結(jié)點占用空間大很多時,索引結(jié)點所占的額外空間(相對原始數(shù)據(jù)來講)又可以忽略不計了。
時間復(fù)雜度
查找的時間復(fù)雜度
來看看時間復(fù)雜度
是如何推導(dǎo)出來的,首先我們看下圖: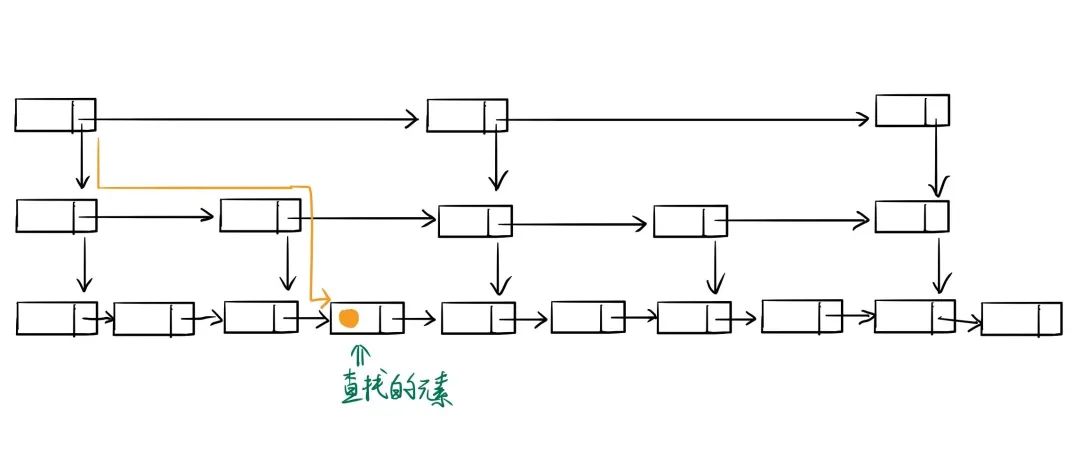
如上圖所示,此處我們假設(shè)每兩個結(jié)點會抽出一個結(jié)點來作為上一級索引的結(jié)點。也就是說,原始鏈表有
個元素,一級索引有
,二級索引有
,k 級索引有
個元素,而最高級索引一般有
個元素。也就是說:最高級索引
滿足
, 由此公式可以得出
, 加上原始數(shù)據(jù)這一層, 跳表的總高度為
。那么,我們在查找過程中每一層索引最多遍歷幾個元素呢?從圖中我們可以看出來每一層最多需要遍歷 3 個結(jié)點。因此,由公式
時間復(fù)雜度 = 索引高度*每層索引遍歷元素個數(shù), 可以得出跳表中查找一個元素的時間復(fù)雜度為
,省略常數(shù)即為
。
插入的時間復(fù)雜度
跳表的插入分為兩部分操作:
尋找到對應(yīng)的位置,時間復(fù)雜度為
,
。因此,我們將數(shù)據(jù)插入到各層索引中的最壞時間復(fù)雜度為
。
綜上所述,插入操作的時間復(fù)雜度為
刪除的時間復(fù)雜度
跳表的刪除操作和查找類似,只是需要在查找后刪除對應(yīng)的元素。查找操作的時間復(fù)雜度是
。那么后面刪除部分代碼的時間復(fù)雜度是多少呢?我們知道在跳表中,每一層索引都是一個有序的單鏈表,而刪除單個元素的復(fù)雜度為
, 索引層數(shù)為
,因此刪除部分代碼的時間復(fù)雜度為
。那么刪除操作的總時間復(fù)雜度為- 。我們忽略常數(shù)部分,刪除元素的時間復(fù)雜度為
。
擴(kuò)展
在工業(yè)上,使用跳表的場景很多,下面做些簡單的介紹,有興趣的可以深入了解:
redis 當(dāng)中 zset 使用了跳表 HBase MemStore 當(dāng)中使用了跳表 LevelDB 和 RocksDB 都是 LSM Tree 結(jié)構(gòu)的數(shù)據(jù)庫,內(nèi)部的 MemTable 當(dāng)中都使用了跳表
配套網(wǎng)站
等新書發(fā)布之后,我們會在官網(wǎng)開辟一個區(qū)域,大家可以直接訪問查看本書配套的配套代碼,包括 JavaScript,Java,Python 和 C++。也歡迎大家留言給我們自己想要支持的語言,我們會鄭重考慮大家的意見。
效果大概是這樣的:

限時優(yōu)惠
五折限時優(yōu)惠,時間到九月中旬
