數(shù)學(xué)三大核心領(lǐng)域概述：代數(shù)、幾何、分析

>>>>

這三大類數(shù)學(xué)構(gòu)成了整個數(shù)學(xué)的本體與核心。在這一核心的周圍，由于數(shù)學(xué)通過數(shù)與形這兩個概念，與其它科學(xué)互相滲透，而出現(xiàn)了許多邊緣學(xué)科和交叉學(xué)科。本文簡要介紹數(shù)學(xué)三大核心領(lǐng)域中十幾門主要分支學(xué)科的有關(guān)歷史發(fā)展情況。

算術(shù)有兩種含義，一種是從中國傳下來的，相當(dāng)于一般所說的“數(shù)學(xué)”，如《九章算術(shù)》等。另一種是從歐洲數(shù)學(xué)翻譯過來的，源自希臘語，有“計算技術(shù)”之意。現(xiàn)在一般所說的“算術(shù)”，往往指自然數(shù)的四則運算；如果是在高等數(shù)學(xué)中，則有“數(shù)論”的含義。作為現(xiàn)代小學(xué)課程內(nèi)容的算術(shù)，主要講的是自然數(shù)、正分?jǐn)?shù)以及它們的四則運算，并通過由計數(shù)和度量而引起的一些最簡單的應(yīng)用題加以鞏固。

算術(shù)是數(shù)學(xué)中最古老的一個分支，它的一些結(jié)論是在長達(dá)數(shù)千年的時間里，緩慢而逐漸地建立起來的。它們反映了在許多世紀(jì)中積累起來，并不斷凝固在人們意識中的經(jīng)驗。

自然數(shù)是在對于對象的有限集合進(jìn)行計算的過程中，產(chǎn)生的抽象概念。日常生活中要求人們不僅要計算單個的對象，還要計算各種量，例如長度、重量和時間。為了滿足這些簡單的量度需要，就要用到分?jǐn)?shù)。

現(xiàn)代初等算術(shù)運算方法的發(fā)展，起源于印度，時間可能在10世紀(jì)或11世紀(jì)。它后來被阿拉伯人采用，之后傳到西歐。15世紀(jì)，它被改造成現(xiàn)在的形式。在印度算術(shù)的后面，明顯地存在著我國古代的影響。

19世紀(jì)中葉，格拉斯曼第一次成功地挑選出一個基本公理體系，來定義加法與乘法運算；而算術(shù)的其它命題，可以作為邏輯的結(jié)果，從這一體系中被推導(dǎo)出來。后來，皮亞諾進(jìn)一步完善了格拉斯曼的體系。

算術(shù)的基本概念和邏輯推論法則，以人類的實踐活動為基礎(chǔ)，深刻地反映了世界的客觀規(guī)律性。盡管它是高度抽象的，但由于它概括的原始材料是如此廣泛，因此我們幾乎離不開它。同時，它又構(gòu)成了數(shù)學(xué)其它分支的最堅實的基礎(chǔ)。

作為中學(xué)數(shù)學(xué)課程主要內(nèi)容的初等代數(shù)，其中心內(nèi)容是方程理論。代數(shù)一詞的拉丁文原意是“歸位”。代數(shù)方程理論在初等代數(shù)中是由一元一次方程向兩個方面擴(kuò)展的：其一是增加未知數(shù)的個數(shù)，考察由有幾個未知數(shù)的若干個方程所構(gòu)成的二元或三元方程組(主要是一次方程組)；其二是增高未知量的次數(shù)，考察一元二次方程或準(zhǔn)二次方程。初等代數(shù)的主要內(nèi)容在16世紀(jì)便已基本上發(fā)展完備了。

古巴比倫(公元前19世紀(jì)～前17世紀(jì))解決了一次和二次方程問題，歐幾里得的《原本》(公元前4世紀(jì))中就有用幾何形式解二次方程的方法。我國的《九章算術(shù)》(公元1世紀(jì))中有三次方程和一次聯(lián)立方程組的解法，并運用了負(fù)數(shù)。3世紀(jì)的丟番圖用有理數(shù)求一次、二次不定方程的解。13世紀(jì)我國出現(xiàn)的天元術(shù)(李冶《測圓海鏡》)是有關(guān)一元高次方程的數(shù)值解法。16世紀(jì)意大利數(shù)學(xué)家發(fā)現(xiàn)了三次和四次方程的解法。

代數(shù)學(xué)符號發(fā)展的歷史，可分為三個階段。第一個階段為三世紀(jì)之前，對問題的解不用縮寫和符號，而是寫成一篇論文，稱為文字?jǐn)⑹龃鷶?shù)。第二個階段為三世紀(jì)至16世紀(jì)，對某些較常出現(xiàn)的量和運算采用了縮寫的方法，稱為簡化代數(shù)。三世紀(jì)的丟番圖的杰出貢獻(xiàn)之一，就是把希臘代數(shù)學(xué)簡化，開創(chuàng)了簡化代數(shù)。然而此后文字?jǐn)⑹龃鷶?shù)，在除了印度以外的世界其它地方，還十分普通地存在了好幾百年，尤其在西歐一直到15世紀(jì)。第三個階段為16世紀(jì)以后，對問題的解多半表現(xiàn)為由符號組成的數(shù)學(xué)速記，這些符號與所表現(xiàn)的內(nèi)容沒有什么明顯的聯(lián)系，稱為符號代數(shù)。16世紀(jì)韋達(dá)的名著《分析方法入門》，對符號代數(shù)的發(fā)展有不少貢獻(xiàn)。16世紀(jì)末，維葉特開創(chuàng)符號代數(shù)，經(jīng)笛卡爾改進(jìn)后成為現(xiàn)代的形式。

“＋”、“－”號第一次在數(shù)學(xué)書中出現(xiàn)，是1489年魏德曼的著作。不過正式為大家所公認(rèn)，作為加、減法運算的符號，那是從1514年由荷伊克開始的。1540年，雷科德開始使用現(xiàn)在使用“＝”。到1591年，韋達(dá)在著作中大量使用后，才逐漸為人們所接受。1600年哈里奧特創(chuàng)用大于號“＞”和小于號“＜”。1631年，奧屈特給出“×”、“÷”作為乘除運算符。1637年，笛卡爾第一次使用了根號，并引進(jìn)用字母表中頭前的字母表示已知數(shù)、后面的字母表示未知數(shù)的習(xí)慣做法。至于“≮”、“≯”、“≠”這三個符號的出現(xiàn)，那是近代的事了。

數(shù)的概念的拓廣，在歷史上并不全是由解代數(shù)方程所引起的，但習(xí)慣上仍把它放在初等代數(shù)里，以求與這門課程的安排相一致。公元前4世紀(jì)，古希臘人發(fā)現(xiàn)無理數(shù)。公元前2世紀(jì)(西漢時期)，我國開始應(yīng)用負(fù)數(shù)。1545年，意大利的卡爾達(dá)諾開始使用虛數(shù)。1614年，英國的耐普爾發(fā)明對數(shù)。17世紀(jì)末，一般的實數(shù)指數(shù)概念才逐步形成。

在高等代數(shù)中，一次方程組（即線性方程組）發(fā)展成為線性代數(shù)理論；而—、二次方程發(fā)展成為多項式理論。前者是向量空間、線性變換、型論、不變量論和張量代數(shù)等內(nèi)容的一門近世代數(shù)分支學(xué)科，而后者是研究只含有一個未知量的任意次方程的一門近世代數(shù)分支學(xué)科。作為大學(xué)課程的高等代數(shù)，只研究它們的基礎(chǔ)。

1683年關(guān)孝和(日本人)最早引入行列式概念。關(guān)于行列式理論最系統(tǒng)的論述，則是雅可比1841年的《論行列式的形成與性質(zhì)》一書。在邏輯上，矩陣的概念先于行列式的概念；而在歷史上，次序正相反。凱雷在1855年引入了矩陣的概念，在1858年發(fā)表了關(guān)于這個課題的第一篇重要文章《矩陣論的研究報告》。

19世紀(jì)，行列式和矩陣受到人們極大的關(guān)注，出現(xiàn)了千余篇關(guān)于這兩個課題的文章。但是，它們在數(shù)學(xué)上并不是大的改革，而是速記的一種表達(dá)式。不過已經(jīng)證明它們是高度有用的工具。

多項式代數(shù)的研究始于對3、4次方程求根公式的探索。1515年，菲洛解決了被簡化為缺2次項的3次方程的求解問題。1540年，費爾拉里成功地發(fā)現(xiàn)了一般4次方程的代數(shù)解法。人們繼續(xù)尋求5次、6次或更高次方程的求根公式，但這些努力在200多年中付諸東流。

1746年，達(dá)朗貝爾首先給出了“代數(shù)學(xué)基本定理”的證明(有不完善之處)。這個定理斷言：每一個實系數(shù)或復(fù)系數(shù)的n次代數(shù)方程，至少有一個實根或復(fù)根。因此，一般地說，n次代數(shù)方程應(yīng)當(dāng)有n個根。1799年，22歲的高斯在寫博士論文中，給出了這個定理的第一個嚴(yán)格的證明。1824年，22歲的阿貝爾證明了：高于4次的一般方程的全部系數(shù)組成的根式，不可能是它的根。1828年，年僅17歲的伽羅華創(chuàng)立了“伽羅華理論”，包含了方程能用根號解出的充分必要條件。

以正整數(shù)作為研究對象的數(shù)論，可以看作是算術(shù)的一部分，但它不是以運算的觀點，而是以數(shù)的結(jié)構(gòu)的觀點，即一個數(shù)可用性質(zhì)較簡單的其它數(shù)來表達(dá)的觀點來研究數(shù)的。因此可以說，數(shù)論是研究由整數(shù)按一定形式構(gòu)成的數(shù)系的科學(xué)。

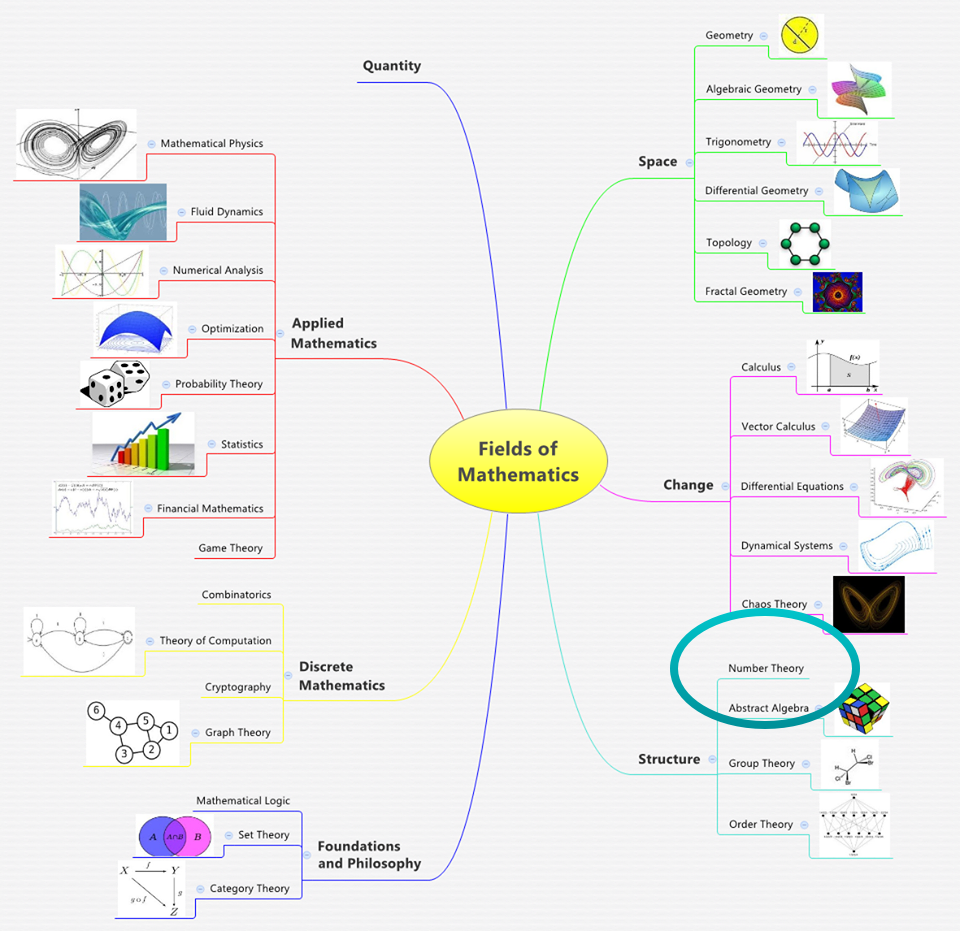
早在公元前3世紀(jì)，歐幾里得的《原本》討論了整數(shù)的一些性質(zhì)。他證明素數(shù)的個數(shù)是無窮的，他還給出了求兩個數(shù)的公約數(shù)的輾轉(zhuǎn)相除法。這與我國《九章算術(shù)》中的“更相減損法”是相同的。埃拉托色尼則給出了尋找不大于給定的自然數(shù)N的全部素數(shù)的“篩法”：在寫出從1到N的全部整數(shù)的紙草上，依次挖去2、3、5、7……的倍數(shù)(各自的2倍，3倍，……)以及1，在這篩子般的紙草上留下的便全是素數(shù)了。

當(dāng)兩個整數(shù)之差能被正整數(shù)m除盡時，便稱這兩個數(shù)對于“模”m同余。我國《孫子算經(jīng)》(公元4世紀(jì))中計算一次同余式組的“求一術(shù)”，有“中國剩余定理”之稱。13世紀(jì)，秦九韶已建立了比較完整的同余式理論——“大衍求一術(shù)”，這是數(shù)論研究的內(nèi)容之一。

丟番圖的《算術(shù)》中給出了求x?＋y?＝z?所有整數(shù)解的方法。費爾馬指出x^n＋y^n＝z^n在n＞3時無整數(shù)解，對于該問題的研究產(chǎn)生了19世紀(jì)的數(shù)論。之后高斯的《數(shù)論研究》(1801年)形成了系統(tǒng)的數(shù)論。

數(shù)論的古典內(nèi)容基本上不借助于其它數(shù)學(xué)分支的方法，稱為初等數(shù)論。17世紀(jì)中葉以后，曾受數(shù)論影響而發(fā)展起來的代數(shù)、幾何、分析、概率等數(shù)學(xué)分支，又反過來促進(jìn)了數(shù)論的發(fā)展，出現(xiàn)了代數(shù)數(shù)論(研究整系數(shù)多項式的根—“代數(shù)數(shù)”)、幾何數(shù)論(研究直線坐標(biāo)系中坐標(biāo)均為整數(shù)的全部“整點”—“空間格網(wǎng)”)。19世紀(jì)后半期出現(xiàn)了解析數(shù)論，用分析方法研究素數(shù)的分布。二十世紀(jì)出現(xiàn)了完備的數(shù)論理論。

1843年，哈密頓發(fā)明了一種乘法交換律不成立的代數(shù)——四元數(shù)代數(shù)。第二年，格拉斯曼推演出更有一般性的幾類代數(shù)。1857年，凱雷設(shè)計出另一種不可交換的代數(shù)——矩陣代數(shù)。他們的研究打開了抽象代數(shù)(也叫近世代數(shù))的大門。實際上，減弱或刪去普通代數(shù)的某些假定，或?qū)⒛承┘俣ù詣e的假定(與其余假定是相容的)，就能研究出許多種代數(shù)體系。

1870年，克隆尼克給出了有限阿貝爾群的抽象定義；狄德金開始使用“體”的說法，并研究了代數(shù)體；1893年，韋伯定義了抽象的體；1910年，施坦尼茨展開了體的一般抽象理論；狄德金和克隆尼克創(chuàng)立了環(huán)論；1910年，施坦尼茨總結(jié)了包括群、代數(shù)、域等在內(nèi)的代數(shù)體系的研究，開創(chuàng)了抽象代數(shù)學(xué)。

1926年，諾特完成了理想(數(shù))理論；1930年，畢爾霍夫建立格論，它源于1847年的布爾代數(shù)；第二次世界大戰(zhàn)后，出現(xiàn)了各種代數(shù)系統(tǒng)的理論和布爾巴基學(xué)派；1955年，嘉當(dāng)、格洛辛狄克和愛倫伯克建立了同調(diào)代數(shù)理論。

到現(xiàn)在為止，數(shù)學(xué)家們已經(jīng)研究過200多種這樣的代數(shù)結(jié)構(gòu)，其中最主要德若當(dāng)代數(shù)和李代數(shù)是不服從結(jié)合律的代數(shù)的例子。這些工作的絕大部分屬于20世紀(jì)，它們使一般化和抽象化的思想在現(xiàn)代數(shù)學(xué)中得到了充分的反映。

抽象代數(shù)是研究各種抽象的公理化代數(shù)系統(tǒng)的數(shù)學(xué)學(xué)科。典型的代數(shù)系統(tǒng)有群、環(huán)、域等，它們主要起源于19世紀(jì)的群論，包含有群論、環(huán)論、伽羅華理論、格論、線性代數(shù)等許多分支，并與數(shù)學(xué)其它分支相結(jié)合產(chǎn)生了代數(shù)幾何、代數(shù)數(shù)論、代數(shù)拓?fù)洹⑼負(fù)淙旱刃碌臄?shù)學(xué)學(xué)科。抽象代數(shù)已經(jīng)成了當(dāng)代大部分?jǐn)?shù)學(xué)的通用語言。

現(xiàn)在，可以籠統(tǒng)地把代數(shù)學(xué)解釋為關(guān)于字母計算的學(xué)說，但字母的含義是在不斷地拓廣的。在初等代數(shù)中，字母表示數(shù)；而在高等代數(shù)和抽象代數(shù)中，字母則表示向量(或n元有序數(shù)組)、矩陣、張量、旋量、超復(fù)數(shù)等各種形式的量。可以說，代數(shù)已經(jīng)發(fā)展成為一門關(guān)于形式運算的一般學(xué)說了。

在希臘語中，“幾何學(xué)”是由“地”與“測量”合并而來的，本來有測量土地的含義，意譯就是“測地術(shù)”。“幾何學(xué)”這個名詞，系我國明代數(shù)學(xué)家根據(jù)讀音譯出的，沿用至今。

現(xiàn)在的初等幾何主要是指歐幾里得幾何，它是討論圖形(點、線、面、角、圓等)在運動下的不變性質(zhì)的科學(xué)。例如，歐氏幾何中的兩點之間的距離，兩條直線相交的交角大小，半徑是r的某一圓的面積等都是一些運動不變量。

初等幾何作為一門課程來講，安排在初等代數(shù)之后；然而在歷史上，幾何學(xué)的發(fā)展曾優(yōu)先于代數(shù)學(xué)，它主要被認(rèn)為是古希臘人的貢獻(xiàn)。

幾何學(xué)舍棄了物質(zhì)所有的其它性質(zhì)，只保留了空間形式和關(guān)系作為自己研究的對象，因此它是抽象的。這種抽象決定了幾何的思維方法，就是必須用推理的方法，從一些結(jié)論導(dǎo)出另一些新結(jié)論。定理是用演繹的方式來證明的，這種論證幾何學(xué)的代表作，便是公元前三世紀(jì)歐幾里得的《原本》，它從定義與公理出發(fā)，演繹出各種幾何定理。

現(xiàn)在中學(xué)《平面三角》中關(guān)于三角函數(shù)的理論是15世紀(jì)才發(fā)展完善起來的，但是它的一些最基本的概念，卻早在古代研究直角三角形時便己形成。因此，可把三角學(xué)劃在初等幾何這一標(biāo)題下。

古代埃及、巴比倫、中國、希臘都研究過有關(guān)球面三角的知識。公元前2世紀(jì)，希帕恰斯制作了弦表，可以說是三角的創(chuàng)始人。后來印度人制作了正弦表；阿拉伯的阿爾·巴塔尼用計算sinθ值的方法來解方程，他還與阿布爾·沃法共同導(dǎo)出了正切、余切、正割、余割的概念；賴蒂庫斯作了較精確的正弦表，并把三角函數(shù)與圓弧聯(lián)系起來。

由于直角三角形是最簡單的直線形，又具有很重要的實用價值，所以各文明古國都極重視它的研究。我國《周髀算經(jīng)》一開始就記載了周朝初年(約公元前1100年左右)的周公與學(xué)者商高的對話，其中就談到“勾三股四弦五”，即勾股定理的特殊形式；還記載了在周公之后的陳子，曾用勾股定理和相似圖形的比例關(guān)系，推算過地球與太陽的距離和太陽的直徑，同時為勾股定理作的圖注達(dá)幾十種之多。在國外，傳統(tǒng)稱勾股定理為畢達(dá)哥拉斯定理，認(rèn)為它的第一個一致性的證明源于畢氏學(xué)派(公元前6世紀(jì))，雖然巴比倫人在此以前1000多年就發(fā)現(xiàn)了這個定理。到現(xiàn)在人們對勾股定理已經(jīng)至少提供了370種證明。

19世紀(jì)以來，人們對于關(guān)于三角形和圓的初等綜合幾何，又進(jìn)行了深入的研究。至今這一研究領(lǐng)域仍然沒有到頭，不少資料已引申到四面體及伴隨的點、線、面、球。

射影幾何學(xué)是一門討論在把點射影到直線或平面上的時候，圖形的不變性質(zhì)的一門幾何學(xué)。幻燈片上的點、線，經(jīng)過幻燈機(jī)的照射投影，在銀幕上的圖畫中都有相對應(yīng)的點線，這樣一組圖形經(jīng)過有限次透視以后，變成另一組圖形，這在數(shù)學(xué)上就叫做射影對應(yīng)。射影幾何學(xué)在航空、攝影和測量等方面都有廣泛的應(yīng)用。

射影幾何是迪沙格和帕斯卡在1639年開辟的。迪沙格發(fā)表了—本關(guān)于圓維曲線的很有獨創(chuàng)性的小冊子，從開普勒的連續(xù)性原理開始，導(dǎo)出了許多關(guān)于對合、調(diào)和變程、透射、極軸、極點以及透視的基本原理，這些課題是今天學(xué)習(xí)射影幾何這門課程的人所熟悉的。年僅16歲的帕斯卡得出了一些新的、深奧的定理，并于9年后寫了一份內(nèi)容很豐富的手稿。18世紀(jì)后期，蒙日提出了二維平面上的適當(dāng)投影表達(dá)三維對象的方法，因而從提供的數(shù)據(jù)能快速算出炮兵陣地的位置，避開了冗長的、麻煩的算術(shù)運算。

射影幾何真正獨立的研究是由彭賽勒開創(chuàng)的。1822年，他發(fā)表了《論圖形的射影性質(zhì)》一文，給該領(lǐng)域的研究以巨大的推動作用。他的許多概念被斯坦納進(jìn)一步發(fā)展。1847年，斯陶特發(fā)表了《位置幾何學(xué)》一書，使射影幾何最終從測量基礎(chǔ)中解脫出來。

后來證明，采用度量適當(dāng)?shù)纳溆岸x，能在射影幾何的范圍內(nèi)研究度量幾何學(xué)。將一個不變二次曲線添加到平面上的射影幾何中，就能得到傳統(tǒng)的非歐幾何學(xué)。在19世紀(jì)晚期和20世紀(jì)初期，對射影幾何學(xué)作了多種公設(shè)處理，并且有限射影幾何也被發(fā)現(xiàn)。事實證明，逐漸地增添和改變公設(shè)，就能從射影幾何過渡到歐幾里得幾何，其間經(jīng)歷了許多其它重要的幾何學(xué)。

解析幾何即坐標(biāo)幾何，包括平面解析幾何和立體解析幾何兩部分。解析幾何通過平面直角坐標(biāo)系和空間直角坐標(biāo)系，建立點與實數(shù)對之間的一一對應(yīng)關(guān)系，從而建立起曲線或曲面與方程之間的一一對應(yīng)關(guān)系，因而就能用代數(shù)方法研究幾何問題，或用幾何方法研究代數(shù)問題。

在初等數(shù)學(xué)中，幾何與代數(shù)是彼此獨立的兩個分支；在方法上，它們也基本是互不相關(guān)的。解析幾何的建立，不僅由于在內(nèi)容上引入了變量的研究而開創(chuàng)了變量數(shù)學(xué)，而且在方法上也使幾何方法與代數(shù)方法結(jié)合起來。

在迪沙格和帕斯卡開辟了射影幾何的同時，笛卡兒和費爾馬開始構(gòu)思現(xiàn)代解析幾何的概念。這兩項研究之間存在一個根本區(qū)別：前者是幾何學(xué)的一個分支，后者是幾何學(xué)的一種方法。

1637年，笛卡兒發(fā)表了《方法論》及其三個附錄，他對解析幾何的貢獻(xiàn)，就在第三個附錄《幾何學(xué)》中，他提出了幾種由機(jī)械運動生成的新曲線。在《平面和立體軌跡導(dǎo)論》中，費爾馬解析地定義了許多新的曲線。在很大程度上，笛卡兒從軌跡開始，然后求它的方程；費爾馬則從方程出發(fā)，然后來研究軌跡。這正是解析幾何基本原則的兩個相反的方面，“解析幾何”的名稱是以后才定下來的。

這門課程達(dá)到現(xiàn)在課本中熟悉的形式，是100多年以后的事。象今天這樣使用坐標(biāo)、橫坐標(biāo)、縱坐標(biāo)這幾個術(shù)語，是萊布尼茲于1692年提出的。1733年，年僅18歲的克雷洛出版了《關(guān)于雙重曲率曲線的研究》一書，這是最早的一部空間解析幾何著作。1748年，歐拉寫的《無窮分析概要》，可以說是符合現(xiàn)代意義的第一部解析幾何學(xué)教程。1788年，拉格朗日開始研究有向線段的理論。1844年，格拉斯曼提出了多維空間的概念，并引入向量的記號。于是多維解析幾何出現(xiàn)了。

解析幾何在近代的發(fā)展，產(chǎn)生了無窮維解析幾何和代數(shù)幾何等一些分支。普通解析幾何只不過是代數(shù)幾何的一部分，而代數(shù)幾何的發(fā)展同抽象代數(shù)有著密切的聯(lián)系。

非歐幾何有三種不同的含義：狹義的，單指羅氏(羅巴切夫斯基)幾何；廣義的，泛指一切和歐氏(歐幾里得)幾何不同的幾何；通常意義的，指羅氏幾何和黎曼幾何。

歐幾里得的第5公設(shè)(平行公設(shè))在數(shù)學(xué)史上占有特殊的地位，它與前4條公設(shè)相比，性質(zhì)顯得太復(fù)雜了。它在《原本》中第一次應(yīng)用是在證明第29個定理時，而且此后似乎總是盡量避免使用它。因此人們懷疑第五公設(shè)的公理地位，并探索用其它公理來證明它，以使它變?yōu)橐粭l定理。在三千多年的時間中，進(jìn)行這種探索并有案可查的就達(dá)兩千人以上，其中包括許多知名的數(shù)學(xué)家，但他們都失敗了。

羅巴契夫斯基于1826年，鮑耶于1832年發(fā)表了劃時代的研究結(jié)果，開創(chuàng)了非歐幾何。在這種幾何中，他們假設(shè)“過不在已知直線上的一點，可以引至少兩條直線平行于已知直線”，用以代替第五公設(shè)，同時保留了歐氏幾何的其它公設(shè)。

1854年，黎曼推出了另一種非歐幾何。在這種幾何中，他假設(shè)“過已知直線外一點，沒有和已知直線平行的直線可引”，用以代替第5公設(shè)，同時保留了歐氏幾何的其它公設(shè)。1871年，克萊因把這3種幾何：羅巴契夫斯基—鮑耶的、歐幾里得的和黎曼的分別定名為雙曲幾何、拋物幾何和橢圓幾何。

非歐幾何的發(fā)現(xiàn)不僅最終解決了平行公設(shè)的問題——平行公設(shè)被證明是獨立于歐氏幾何的其它公設(shè)的，而且把幾何學(xué)從其傳統(tǒng)模型中解放出來，創(chuàng)造了許多不同體系的幾何的道路被打開了。

1854年，黎曼發(fā)表了“關(guān)于作為幾何學(xué)基礎(chǔ)的假設(shè)的講演”。他指出：每種不同的(兩個無限靠近的點的)距離公式?jīng)Q定了最終產(chǎn)生的空間和幾何的性質(zhì)。1872年，克萊因建立了各種幾何系統(tǒng)按照不同變換群不變量的分類方法。

19世紀(jì)以后，幾何空間概念發(fā)展的另一方向，是按照所研究流形的微分幾何原則的分類，每一種幾何都對應(yīng)著一種定理系統(tǒng)。1899年，希爾伯特發(fā)表了《幾何基礎(chǔ)》一書，提出了完備的幾何公理體系，建立了歐氏幾何的嚴(yán)密的基礎(chǔ)，并給出了證明一個公理體系的相容性(無矛盾性)、獨立性和完備性的普遍原則。按照他的觀點，不同的幾何空間乃是從屬于不同幾何公理要求的元素集合。歐氏幾何和非歐幾何，在大量的幾何系統(tǒng)中，只不過是極其特殊的情形罷了。

1736年，歐拉發(fā)表論文，討論哥尼斯堡七橋問題。他還提出球面三角形剖分圖形頂點、邊、面之間關(guān)系的歐拉公式，這可以說是拓?fù)鋵W(xué)的開端。

龐加萊于1895～1904年建立了拓?fù)鋵W(xué)，采用代數(shù)組合的方法研究拓?fù)湫再|(zhì)。他把歐拉公式推廣為歐拉—龐加萊公式，與此有關(guān)的理論現(xiàn)在稱為同調(diào)理論和同倫理論。以后的拓?fù)鋵W(xué)主要按照龐加萊的設(shè)想發(fā)展。

拓?fù)鋵W(xué)開始是幾何學(xué)的一個分支，在二十世紀(jì)它得到了極大的推廣。1906年，弗雷歇發(fā)表博士論文，把函數(shù)作為一個“點”來看，把函數(shù)收斂描繪成點的收斂，這就把康托的點集論和分析學(xué)的抽象化聯(lián)系起來了。他在函數(shù)所構(gòu)成的集合中引入距離的概念，構(gòu)成距離空間，展開了線性距離空間的理論。在這個基礎(chǔ)上，產(chǎn)生了點集拓?fù)鋵W(xué)。在豪斯道夫的《點集論綱要》一書中，出現(xiàn)了更一般的點集拓?fù)鋵W(xué)的完整想法。第二次世界大戰(zhàn)后，把分析引進(jìn)拓?fù)洌l(fā)展了微分拓?fù)洹?/span>

現(xiàn)在的拓?fù)鋵W(xué)可以粗略地定義為對于連續(xù)性的數(shù)學(xué)研究。任何事物的集合都能在某種意義上構(gòu)成拓?fù)淇臻g，拓?fù)鋵W(xué)的概念和理論已基本完組成為數(shù)學(xué)的基礎(chǔ)理論之一，滲入到各個分支，并且成功地應(yīng)用于電磁學(xué)和物理學(xué)的研究。

微積分學(xué)是微分學(xué)和積分學(xué)的統(tǒng)稱，它是研究函數(shù)的導(dǎo)數(shù)、積分的性質(zhì)和應(yīng)用的一門數(shù)學(xué)分支學(xué)科。

微積分的出現(xiàn)具有劃時代意義，時至今日，它不僅成了學(xué)習(xí)高等數(shù)學(xué)各個分支必不可少的基礎(chǔ)，而且是學(xué)習(xí)近代任何一門自然科學(xué)和工程技術(shù)的必備工具。現(xiàn)在的微積分學(xué)的教程，通常的講授次序是先極限、再微分、后積分，這與歷史順序正好相反。

在微積分歷史中，最初的問題是涉及計算面積、體積和弧長的。阿基米得(公元前3世紀(jì))的方法最接近于現(xiàn)行的積分法。在17世紀(jì)探索微積分的至少有十幾位大數(shù)學(xué)家和幾十位小數(shù)學(xué)家。牛頓和萊布尼茨分別進(jìn)行了創(chuàng)造性的工作，各自獨立地跑完了“微積分這場接力賽的最后一棒”。

1609年，開普勒為了計算行星運動第二定律中包含的面積，和在他的論文中討論的酒桶的體積，而借助了某種積分方法。1635年，卡瓦列利發(fā)表了一篇闡述不可分元法的論文，提出卡瓦列利原理，它是計算面積和體積的有價值的工具。1650年，沃利斯把卡瓦列利的方法系統(tǒng)化，并作了推廣。

微分起源于作曲線的切線和求函數(shù)的極大值或極小值問題。雖然可以追溯到古希臘，但是第一個真正值得注意的先驅(qū)工作，是費爾馬1629年陳述的概念。1669年，巴羅對微分理論作出了重要的貢獻(xiàn)，他用了微分三角形，很接近現(xiàn)代微分法。一般認(rèn)為，他是充分地認(rèn)識到微分法為積分法的逆運算的第一個人。

至此，還有什么要做的呢？首要的是，創(chuàng)造一般的符號和一整套形式的解析規(guī)則，形成可以應(yīng)用的微積分學(xué)，這項工作是由牛頓和萊布尼茲彼此獨立地做出的。接著的工作是在可接受的嚴(yán)格的基礎(chǔ)上，重新推導(dǎo)基本理論，這必須等到此課題想到多方面應(yīng)用之后。柯西和他的后繼者們完成了這一工作。

牛頓早在1665年才23歲時，就創(chuàng)造了流數(shù)法(微分學(xué))，并發(fā)展到能求曲線上任意一點的切線和曲率半徑。他的《流數(shù)法》寫于1671年，但直到死后9年的1736年才發(fā)表。牛頓考慮了兩種類型的問題，等價于現(xiàn)在的微分和解微分方程。他定義了流數(shù)(導(dǎo)數(shù))、極大值、極小值、曲線的切線、曲率、拐點、凸性和凹性，并把它的理論應(yīng)用于許多求積問題和曲線的求長問題。

牛頓創(chuàng)立的微積分原理是同他的力學(xué)研究分不開的，他借此發(fā)現(xiàn)、并研究了力學(xué)三大定律和萬有引力定律，1687年出版了名著《自然哲學(xué)的數(shù)學(xué)原理》。這本書是研究天體力學(xué)的，包括了微積分的一些基本概念和原理。

萊布尼茨是在1673年到1676年之間，從幾何學(xué)觀點上獨立發(fā)現(xiàn)微積分的。1676年，他第一次用長寫字母∫表示積分符號，象今天這樣寫微分和微商。1684年～1686年，他發(fā)表了一系列微積分著作，力圖找到普遍的方法來解決問題。今天課本中的許多微分的基本原則就是他推導(dǎo)出來的，如求兩個函數(shù)乘積的n階導(dǎo)數(shù)的法則，現(xiàn)在仍稱作菜布尼茲法則。萊布尼茲的另一最大功績是創(chuàng)造了反映事物本質(zhì)的數(shù)字符號，數(shù)學(xué)分析中的基本概念的記號，例如微分dx，二級微分dx?，積分∫ydx，導(dǎo)數(shù)dy/dx等都是他提出來的，并且沿用至今，非常方便。

牛頓與萊布尼茨的創(chuàng)造性工作有很大的不同。主要差別是牛頓把x和y的無窮小增量作為求導(dǎo)數(shù)的手段，當(dāng)增量越來越小的時候，導(dǎo)數(shù)實際上就是增量比的極限，而萊布尼茲卻直接用x和y的無窮小增量(就是微分)求出它們之間的關(guān)系。

這個差別反映了他們研究方向的不同，在牛頓的物理學(xué)方向中，速度之類是中心概念；而在萊布尼茲的幾何學(xué)方向中，卻著眼于面積體積的計算。其它差別是，牛頓自由地用級數(shù)表示函數(shù)，采用經(jīng)驗的、具體和謹(jǐn)慎的工作方式，認(rèn)為用什么記號無關(guān)緊要；而萊布尼茲則寧愿用有限的形式來表示函數(shù)，采用富于想象的、喜歡推廣的、大膽的工作方式，花費很多時間來選擇富有提示性的符號。

到1700年，現(xiàn)在大學(xué)且學(xué)習(xí)的大部分微積分內(nèi)容已經(jīng)建立起來。第一部微積分課本出版于1696年，是洛比達(dá)寫的。1769年，歐拉論述了二重積分。1773年，拉格朗日考察了三重積分。1837年，波爾查諾給出了級數(shù)的現(xiàn)代定義。19世紀(jì)分析學(xué)的嚴(yán)謹(jǐn)化，是由柯西奠基的。現(xiàn)在課本中的極限、連續(xù)性定義、把導(dǎo)數(shù)看作差商的極限、把定積分看做和的權(quán)限等等，實質(zhì)上都是柯西給出的。進(jìn)一步完成這一工作的是威爾斯特拉斯，他給出了現(xiàn)在使用的精確的極限定義，并同狄德金、康托于19世紀(jì)70年代建立了嚴(yán)格的實數(shù)理論，使微積分有了堅固可靠的邏輯基礎(chǔ)。

凡是表示未知函數(shù)和未知函數(shù)的導(dǎo)數(shù)以及自變量之間的關(guān)系的方程，就叫做微分方程。如果未知函數(shù)是一元函數(shù)，則稱為常微分方程，如果未知函數(shù)是多元函數(shù)，則稱為偏微分方積。微分方程的基本問題是在一定條件下，從所給出的微分方程解出未知函數(shù)。

微分方程幾乎是與微積分同時發(fā)展起來的，由于它與力學(xué)、物理學(xué)的淵源很深，所以在13世紀(jì)便已自成一門獨立的學(xué)科了。兩個多世紀(jì)來，這一學(xué)科已發(fā)展得相當(dāng)完善。

1676年，萊布尼茲在致牛頓的信中，首先提出了“微分方程”這個名稱。在他們兩人的著作中，都包含了許多微分方程的實例。早期的研究側(cè)重于探討各類一階方程的解法，并由此導(dǎo)致了方程的分類。18世紀(jì)，歐拉解決了全微分方程和“歐拉方程”(一類高階變系數(shù)線性微分方程)，提出了通解和特解的概念，指出了n階線性方程通解的結(jié)構(gòu)。其后，泰勒得到了方程的奇解；拉格朗日推導(dǎo)了非齊次線性方程的常數(shù)交易法。

對于微分方程組的研究，始于達(dá)朗貝爾。19世紀(jì)前半葉，柯西開始研究解的存在性和唯一性。19世紀(jì)后半葉，數(shù)學(xué)家們開始利用群論來研究微分方程，由此建立連續(xù)群和李群的新理論。龐加萊引入了極限環(huán)的概念，李雅普諾夫引入了微分方程組解的穩(wěn)定性概念。他們的方法都不必直接求解，稱為定性理論。1927年，畢爾霍夫建立了“動力系統(tǒng)”的一段定性理論。

一階偏微分方程的研究首先是從幾何學(xué)問題開始的。拉格朗日指出，解一階線性偏微分方程的技巧，在于把它們化為常微分方程。一階非線性偏微分方程的研究，始于歐拉和拉格朗日，蒙日為偏微分方程的幾何理論奠定了基礎(chǔ)。到18世紀(jì)末葉，在引入奇解、通解、全積分、通積分、特積分等概念之后，偏微分方程已形成一門獨立的學(xué)科。

二階偏微分方程的研究，始于18世紀(jì)的弦振動理論。通常見的二階偏微分方程均來自物理或力學(xué)的實際問題，它們構(gòu)成了這門學(xué)科中一個獨立的系統(tǒng)—數(shù)學(xué)物理方程。

積分方程源于阿貝爾1826年的工作，但是直到1888年杜·波阿·雷蒙的著作中，才正式提出了積分方程這個名詞。1896年開始，伏特拉給出了兩類積分方程的一般理論；不久，弗雷德荷姆大體上完成了一類重要的線性積分方程理論。由于這類積分方程常出現(xiàn)在一些物理問題中，因此積分方程論常被包含在數(shù)學(xué)物理方程內(nèi)。

現(xiàn)代科學(xué)技術(shù)，如空間技術(shù)、現(xiàn)代物理學(xué)、力學(xué)等，都有許多問題需要用微分方程來求解，甚至在化學(xué)、生物學(xué)、醫(yī)藥學(xué)、經(jīng)濟(jì)學(xué)等方面，微分方程的應(yīng)用也越來越多。

微分幾何這門分支學(xué)科主要研究三維歐氏空間中曲線和曲面的內(nèi)在性質(zhì)，所謂內(nèi)在性質(zhì)就是同幾何對象在空間中的位置無關(guān)的性質(zhì)。它以微積分、微分方程這些分支學(xué)科的理論為研究工具。或簡單地說，微分幾何就是用分析方法研究幾何性質(zhì)。

微分幾何的發(fā)端可見于1731年克萊洛的著作中。蒙日1809年的著作包含了這一學(xué)科的雛型；歐拉研究了曲面的一般理論；高斯1827年的《關(guān)于曲面的一般研究》一書，論述了曲面理論，創(chuàng)立了內(nèi)蘊(yùn)幾何學(xué)，奠定了曲面微分幾何的基礎(chǔ)。1887～1896年，達(dá)布的《曲面一般理論的講義》集曲線和曲面微分幾何之大成。

變換理論對于微分幾何的影響，產(chǎn)生了射影微分幾何、仿射微分幾何等分支。二十世紀(jì)初，出現(xiàn)了對非充分光滑曲線和曲面以及曲線曲面的整體問題的研究，形成現(xiàn)代微分幾何。1923年，嘉當(dāng)提出了一般聯(lián)絡(luò)的理論。1945年，陳省身建立了代數(shù)拓?fù)浜臀⒎謳缀蔚穆?lián)系，他又是纖維叢概念的創(chuàng)建人之一。

函數(shù)論包括復(fù)變函數(shù)論和實變函數(shù)論，但有時也單指復(fù)變函數(shù)論(或復(fù)分析)而言。

復(fù)數(shù)概念出現(xiàn)于16世紀(jì)，但對它的全面掌握和廣泛運用，卻遲至18世紀(jì)。自變量是復(fù)數(shù)的函數(shù)，叫做復(fù)變函數(shù)。如果復(fù)變函數(shù)在某一區(qū)域內(nèi)除了可能有有限個例外點之外，處處有導(dǎo)數(shù)，那么這個伏辯函數(shù)叫做在這個區(qū)域內(nèi)的解析函數(shù)；例外點叫做奇點。復(fù)變函數(shù)論主要研究解析函數(shù)的性質(zhì)。

復(fù)變函數(shù)的研究是從18世紀(jì)開始的。30～40年代，歐拉利用冪級數(shù)詳細(xì)討論了初等復(fù)變函數(shù)的性質(zhì)。達(dá)朗貝爾于1752年得出復(fù)變函數(shù)可微的必要條件(即“柯西—黎曼條件”)。拉普拉斯也考慮過復(fù)變函數(shù)的積分。

復(fù)變函數(shù)的全面發(fā)展是在19世紀(jì)。1825年，柯西討論了虛限定積分，1831年他實質(zhì)上推出了柯西積分公式，并在此基礎(chǔ)上建立了一整套復(fù)變函數(shù)微分和積分的理論。黎曼1851年的博士論文《復(fù)變函數(shù)論的基礎(chǔ)》，奠定了復(fù)變函數(shù)論的基礎(chǔ)。他推廣了單位解析函數(shù)到多位解析函數(shù)；引入了“黎曼曲面”的重要概念，確立了復(fù)變因數(shù)的幾何理論基礎(chǔ)；證明了保角映射基本定理。威爾斯特拉斯完全擺脫了幾何直觀，以冪級數(shù)為工具，用嚴(yán)密的純解析推理展開了函數(shù)論。定義解析函數(shù)是可以展開為冪級數(shù)的函數(shù)，圍繞著奇點研究函數(shù)的性質(zhì)。近幾十年來，復(fù)變函數(shù)論又有很大的推進(jìn)。

復(fù)變函數(shù)論是解決工程技術(shù)問題的有力工具，飛機(jī)飛行理論、熱運動理論、流體力學(xué)理論、電場和彈性理論等中的很多問題。

實變函數(shù)的發(fā)展較晚，其中積分論是它的重要組成部分。容度和測度是線段長度概念的推廣，是為了推廣積分的概念而建立起來的。1893年，約當(dāng)給出了“約當(dāng)容度”的概念，并用于討論積分。1894年，斯提捷首先推廣了積分概念，得到了“斯提捷積分”。1898年，波萊爾改進(jìn)了容度的概念，他稱之為‘測度”。下一步?jīng)Q定性的進(jìn)展是1902年勒貝格改進(jìn)了測度理論，建立了“勒貝格測度”、“勒貝格積分”等概念。1904年，他完全解決了黎曼可積性的問題。后來，數(shù)學(xué)家們對積分的概念又作了種種推廣和探索。

實變函數(shù)的另一個領(lǐng)域是函數(shù)構(gòu)造論。1885年，威爾斯特拉斯證明：連續(xù)函數(shù)必可表示為一致收斂的多項式級數(shù)。這一結(jié)果和切比雪夫斯基最佳逼近論，是函數(shù)構(gòu)造論的開端。近年來，這個方向的研究十分活躍。

本世紀(jì)初，出現(xiàn)了一個廣闊的新領(lǐng)域——泛函分析，它是古典分析觀點的推廣。近幾十年來，由于分析學(xué)中許多新分支的形成，從而發(fā)現(xiàn)在代數(shù)、幾何、分析中不同領(lǐng)域之間的某些方面的類似。其次，幾何與集合論的結(jié)合產(chǎn)生了抽象空間的理論，將函數(shù)看成函數(shù)空間中的點。再加上實變函數(shù)論以及近世代數(shù)的感念和方法的影響，就產(chǎn)生了泛函分析。它綜合函數(shù)論，幾何和代數(shù)的觀點，研究無窮維向量空間上的函數(shù)、算子和極限理論。

19世紀(jì)末，弗爾太拉和二十世紀(jì)初阿達(dá)瑪?shù)闹髦幸殉霈F(xiàn)泛函分析的萌芽。隨后希爾伯特、海令哲開創(chuàng)了“希爾伯將空間”的研究，黎斯、馮·諾伊曼等人在這方面都有重要的建樹。

—?THE END —

?為什么我國的博士越來越“少”？30歲真的是搞科研最難的年紀(jì)嗎？

?年僅43歲！知名大學(xué)教授、博導(dǎo)，工作期間突發(fā)疾病去世

?無窮的藝術(shù)

?鄧亞萍談決定讀博士的原因，什么年齡都不要停止自己進(jìn)步！

?官宣！多所高校，整體搬遷！

?多位中青年科研人員早逝！985教授：不要拿生命做研究