生成模型那些事:從 VAE 到擴散模型

1. 為什么叫擴散模型

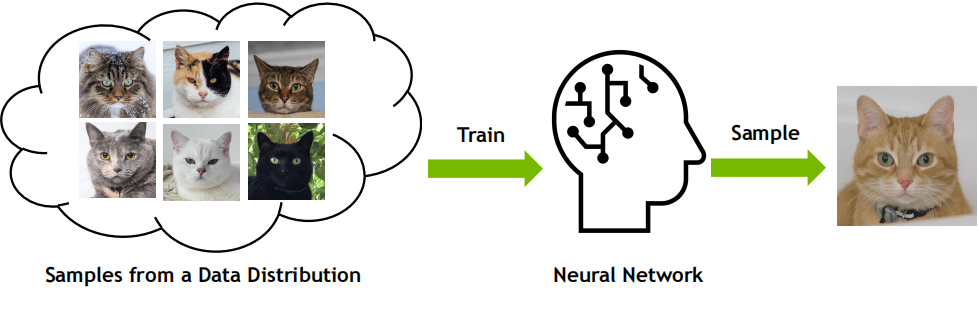
擴散模型的全稱是擴散概率模型，通過將真實數(shù)據(jù)樣本擴散到一個簡單分布，再從該簡單分布中采樣生成新的樣本，從而實現(xiàn)生成模型的功能。

簡單說，就是化繁為簡。模型的學(xué)習(xí)目標是數(shù)據(jù)呈現(xiàn)或服從的分布，將復(fù)雜分布逐步轉(zhuǎn)移到簡單分布，再從簡單分布開始逐步生成呈復(fù)雜分布的數(shù)據(jù)。 這里可能有些問題：

1、何為簡單，何為復(fù)雜？

一般來說，如果一個事物的概率分布很難用簡潔的數(shù)學(xué)公式或模型來表達，那么我們就認為這個事物是復(fù)雜的；反之，如果一個事物的概率分布可以用簡單的數(shù)學(xué)公式或模型來表達，那么我們就認為這個事物是簡單的。

一般而言，比較簡單的分布有如二項分布、均勻分布，以及更加廣泛的正態(tài)分布。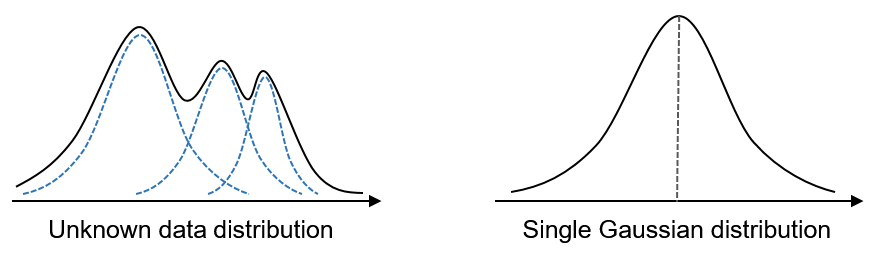 還有一層含義是隨機變量之間的關(guān)系，相互獨立則為簡單，相關(guān)性高則為復(fù)雜。

2、擴散模型這個名頭又是怎么來的呢？換句話說，為什么叫擴散模型呢？

Sohl-Dickstein 于 2015 年提出擴散模型，當(dāng)時其正熱衷于研究生成模型，同時又對非平衡熱力學(xué)感興趣。擴散模型的靈感來自于物理學(xué)中非平衡熱力學(xué)系統(tǒng)的演化過程。在非平衡熱力學(xué)系統(tǒng)中，系統(tǒng)的熵會隨著時間不斷增加，最終達到平衡狀態(tài)。

非平衡熱力學(xué)也稱不可逆過程熱力學(xué)，一切不可逆過程都是系統(tǒng)某一性質(zhì)在物系內(nèi)部的輸運過程，其原因是系統(tǒng)的相應(yīng)的另一性質(zhì)的不均勻性，如溫差引起熱傳導(dǎo)、濃度差異引起擴散等現(xiàn)象。

就這里涉及的擴散，我們不妨來舉一個例子，即一滴紫色墨水在水杯中擴散的過程。起初，它在一個地方形成了一個深色斑點。此時，如果想計算在容器的某個小體積內(nèi)找到一墨水分子的概率，則需要一個能清晰地模擬初始狀態(tài)的概率分布，即墨水開始擴散之前的狀態(tài)。但這個分布很復(fù)雜，因此難以從中采樣。

然而，最終墨水在整個水杯中擴散，使其變得淡紫。這導(dǎo)致了一個更簡單、更均勻的分子概率分布，可以用簡單的數(shù)學(xué)表達式描述。非平衡熱力學(xué)描述了擴散過程中每一步的概率分布。關(guān)鍵是，每一步都是可逆的，通過足夠小的步驟，你可以從簡單分布回到復(fù)雜分布。 Sohl-Dickstein 受擴散原理啟發(fā)提出了一種生成建模算法。這個想法很簡單：算法首先將數(shù)據(jù)集中的復(fù)雜圖像轉(zhuǎn)化為簡單的噪聲，這類似于從一滴墨水變成擴散后的均勻淺色水，然后讓模型學(xué)習(xí)如何反轉(zhuǎn)該過程，即將噪聲轉(zhuǎn)化為圖像。

這里有一點比較有趣，那就是非平衡熱力學(xué)涉及的是不可逆過程，而擴散模型中神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)的偏偏就是那個逆過程。這其實也不難解釋，物理上或許不可逆，但邏輯上考慮這個可逆過程自然是沒有問題的嘛。

雖然早在 2015 年就發(fā)布擴散模型算法，但當(dāng)時遠遠落后于 GAN 的效果。雖然擴散模型可以對整個分布進行采樣，但圖像看起來更糟，而且過程非常慢。在經(jīng)過大約四五年的慢慢擴散，孕育出如 DDPM、DDIM 等后續(xù)工作，讓擴散模型這個方向逐漸趨于成熟。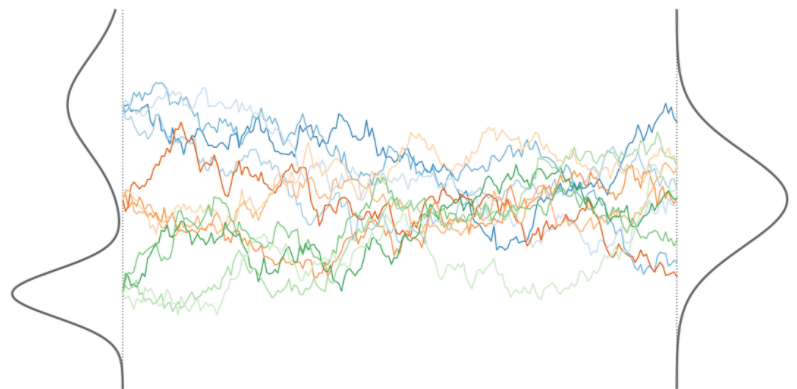 兩個分布之間似乎存在很大的鴻溝，那么擴散模型是如何建模兩個分布之間的轉(zhuǎn)換呢？這也是跟其他模型，如 VAE 之類的區(qū)別所在，在擴散模型中兩個分布之間的轉(zhuǎn)化并不是一蹴而就或一步到位的，而是逐步轉(zhuǎn)換。而且，前向擴散中的每一步的轉(zhuǎn)換可以是固定的，是不需要學(xué)習(xí)的，只有反向擴散過程才是需要學(xué)習(xí)的。

2. 與 VAE 的關(guān)系

傳統(tǒng)的深度生成模型，例如變分自編碼器 (VAE) 和生成對抗網(wǎng)絡(luò) (GAN)，在學(xué)習(xí)復(fù)雜數(shù)據(jù)分布時面臨一些挑戰(zhàn)。其中一個主要挑戰(zhàn)是難以找到合適的概率分布來精確表示數(shù)據(jù)。此外，這些模型通常需要大量的訓(xùn)練數(shù)據(jù)才能獲得良好的性能。

2015 年發(fā)表的論文 Deep Unsupervised Learning using Nonequilibrium Thermodynamics，提出了一種基于隨機微分方程（SDE）的深度生成模型，通過模擬數(shù)據(jù)分布的擴散過程來進行無監(jiān)督學(xué)習(xí)。

受非平衡統(tǒng)計物理學(xué)啟發(fā)，其基本思想是通過迭代前向擴散過程系統(tǒng)地、緩慢地消除數(shù)據(jù)分布中的結(jié)構(gòu)。然后，學(xué)習(xí)反向擴散過程，逐步恢復(fù)數(shù)據(jù)分布中的潛在結(jié)構(gòu)。

該算法首先從一個隨機噪聲狀態(tài)開始，然后逐漸模擬向目標數(shù)據(jù)分布的演化過程。在演化過程中，模型會不斷學(xué)習(xí)數(shù)據(jù)分布的潛在結(jié)構(gòu)，并最終能夠生成與目標數(shù)據(jù)分布相似的樣本。

這種模型的優(yōu)點是具有高度的靈活性和可計算性，但也存在一些缺點，如采樣速度慢，訓(xùn)練不穩(wěn)定，難以擬合復(fù)雜的數(shù)據(jù)分布等。

2020 年發(fā)表的論文 Denoising Diffusion Probabilistic Models（簡稱 DDPM）對原始的擴散模型進行了改進，通過引入變分推斷（variational inference）的方法，將擴散過程分解為兩個參數(shù)化的馬爾可夫鏈，一個是前向（正向）的擾動數(shù)據(jù)的鏈，另一個是反向的恢復(fù)數(shù)據(jù)的鏈。這種方法的優(yōu)點是可以有效地最大化數(shù)據(jù)的邊緣似然，提高采樣的質(zhì)量和速度，增強模型的泛化能力和穩(wěn)健性。

可以說 DDPM 是對原始擴散模型的一種擴展和改進，它解決了前者的一些限制和問題，使得擴散模型成為了一種強大的深度生成模型。

? VAE 與擴散模型

本文主要講述 DDPM 中改進的擴散模型。由于擴散模型一方面也是類似于 VAE，因此我們有必要回顧一下 VAE。

對于生成模型，一般不在數(shù)據(jù)變量 所在空間直接生成數(shù)據(jù)，因為它往往位于所在空間中的一個低維流形上。因此生成模型也可以看作是對數(shù)據(jù)流形的一種參數(shù)化，參數(shù)所在空間在維度上往往比數(shù)據(jù)空間要低。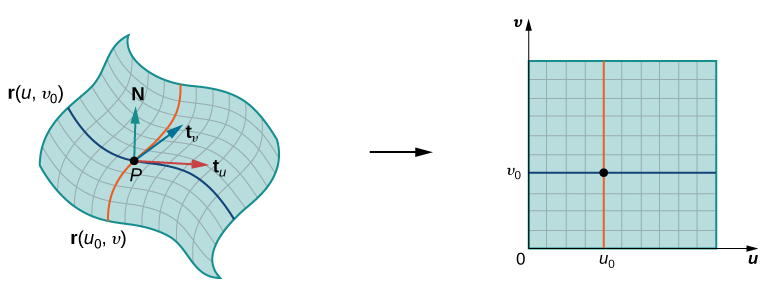 這個時候數(shù)據(jù) 與參數(shù) 是一一對應(yīng)的，也是確定的，因此是確定性生成模型。然而，VAE 和擴散模型不是確定性模型，而是概率生成模型，數(shù)據(jù) 與參數(shù) 并不是一一對應(yīng)的，而是對應(yīng)一定概率。此時的 一般稱為隱變量，數(shù)據(jù)變量和隱變量的聯(lián)合概率記為 。而參數(shù)化好比估計后驗概率  。

回到 VAE，我們的目標是要對數(shù)據(jù)分布進行建模。首先引入隱變量 ，設(shè)定模型并最大化

為了便于計算實際中往往是最大化 ，并求后驗概率 以及似然 。然后將數(shù)據(jù)變量和隱變量的聯(lián)合概率 邊緣化并取對數(shù)，

然后再通過最大化數(shù)據(jù)的證據(jù)下限（ELBO）來學(xué)習(xí)模型的參數(shù)。

當(dāng)然，上述只是針對一個數(shù)據(jù)點，最終是在整個訓(xùn)練集或小批量數(shù)據(jù)上訓(xùn)練，也就是最大化 。

現(xiàn)在考慮擴散概率模型，相對于 VAE，這里引入的隱變量不是一個，而是一個系列，可以記為 。所有生成變量的相應(yīng)聯(lián)合分布由 給出，一般會寫成 ，本文的寫法主要是為了突出隱變量。

類似于 VAE，我們有，

簡單說，擴散模型是一個參數(shù)化的馬爾可夫鏈，使用變分推斷來訓(xùn)練，以在有限時間步驟內(nèi)產(chǎn)生與數(shù)據(jù)匹配的樣本。

? 分層變分自編碼器

擴散模型可以看作一個特殊的分層式馬爾可夫變分自編碼器。生成過程涉及的是隨機變量的轉(zhuǎn)換，但是擴散模型是逐步轉(zhuǎn)換的，不像 VAE 那么一步到位，因此具有更明確的路線圖。具體來說，它是一種分層変分自編碼器（HVAE）。

分層變分自編碼器是 VAE 的推廣，可擴展到含有多個層次結(jié)構(gòu)的隱變量系列。其中的隱變量本身被解釋為從其他更高級別、更抽象的隱變量生成。

雖然在具有 層結(jié)構(gòu)的一般 HVAE 中，每個隱變量都可以以所有先前的隱變量為條件，但在這里我們重點關(guān)注一種特殊情況，稱為馬爾可夫 HVAE，即MHVAE。在 MHVAE 中，生成過程是一個馬爾可夫鏈；也就是說，層次結(jié)構(gòu)中的轉(zhuǎn)換都是馬爾可夫的，其中解碼每個隱變量 僅以先前的隱變量 為條件。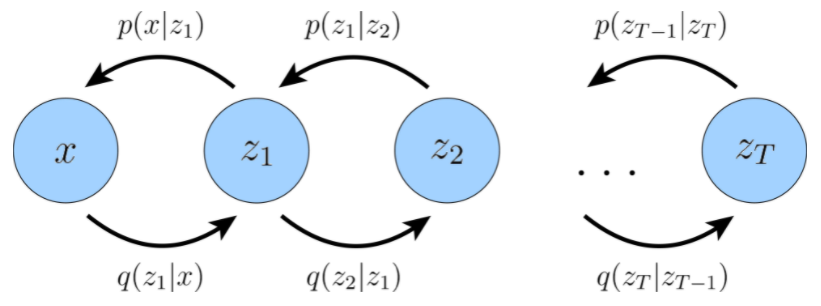 直觀和視覺上，這可以看作是簡單地將 VAE 堆疊在一起，如上圖所示。在數(shù)學(xué)上，我們將馬爾可夫分層變分自編碼器的聯(lián)合分布表示為：

其后驗為：

然后，我們可以將 VAE 中的 ELBO 擴展為：

然后，我們可以將式 的聯(lián)合分布和式 的后驗分布代入式 以生成替代形式：

當(dāng)我們研究變分擴散模型時，這個目標可以進一步分解為可解釋的組件。

3. 擴散模型

? 前向擴散過程

前向擴散過程對應(yīng)如下馬爾科夫鏈，

隱變量系列 其中，。我們配上噪聲數(shù)據(jù)和圖像數(shù)據(jù)，就是如下這種圖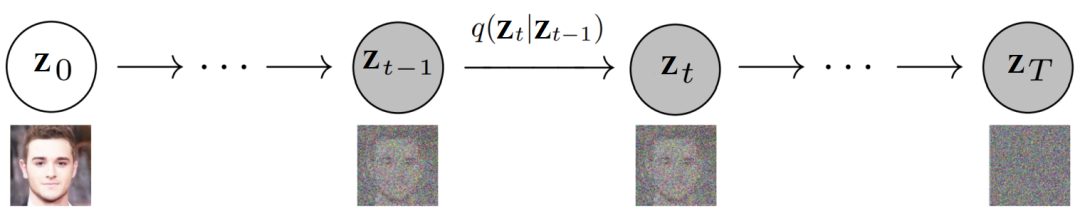， 具體來說，前向擴散過程中的分布 定義為一個馬爾可夫鏈，如下所示：

其中， 被稱為前向擴散核（FDK），不像在 VAE 中那樣需要學(xué)習(xí)參數(shù)，擴散模型（如 DDPM）中采用如下高斯分布，

• 它定義了前向擴散過程中時間步 處當(dāng)給定圖像 后圖像 的 PDF。

• 它表示前向擴散過程中每一步用到的“轉(zhuǎn)移函數(shù)”。

此處，有幾點需要了解，

1）我們首先從數(shù)據(jù)集中獲取圖像：。從數(shù)學(xué)上講，它相當(dāng)于從原始（但未知的）數(shù)據(jù)分布中采樣數(shù)據(jù)點，即 。

2）前向擴散過程的 PDF 是從時間步 開始的單獨分布的乘積。

3）前向擴散過程是固定且已知的，因此不需要學(xué)習(xí)，所以涉及的分布沒有寫成 。

4）從時間步 到 開始的所有中間加噪圖像都稱為隱變量，隱變量的維度與原始圖像的相同。

5）用于定義 FDK 的 PDF 是正態(tài)分布。

6）在每個時間步 ，定義圖像 分布的參數(shù)設(shè)置為：

• 均值： ；

• 協(xié)方差：。

重參數(shù)化技巧

首先，我們設(shè)定一個前向擴散過程，在總共 個步驟中逐步向樣本添加少許高斯噪聲，產(chǎn)生一系列隱變量 ，，，涉及的步長由一個預(yù)設(shè)的方差表 給出。

隨著步長 變大，數(shù)據(jù)變量 逐漸失去其可區(qū)分的特征。最終當(dāng) 時， 等價于各向同性的高斯分布。

下面，我們來看一下這一過程中的具體步驟。

先看前向擴散過程中的某一步，，該步驟可以寫為，

其中， 以及 。

從上面公式可以看出該步驟是先將 縮小，再加上方差為 的高斯噪聲，因此數(shù)據(jù) 肉眼可見得逐步被轉(zhuǎn)換成標準高斯噪聲。

把上式的 換成 ，則有

沿著這個路子不斷展開，可得，

其中， 以及 ，，，， 。

注意，公式中涉及到了兩個高斯分布 和 的合并操作，結(jié)果是一個新的高斯分布 。上式中，使用重新參數(shù)化技巧將來自合并后分布的樣本表示為 。

上述過程意味著我們可以使用重新參數(shù)化技巧在任意時間步對 直接進行采樣。也就是說不需要按逐步加噪方式來操作，我們可以一步到位，直接用 表示 ，

值得強調(diào)的是，前向擴散過程是預(yù)先固定的，因此并沒有參數(shù)需要學(xué)習(xí)。需要學(xué)習(xí)的正是反向擴散過程中的模型參數(shù)，下面就來看看是怎么回事。

? 反向擴散過程

模型的前向過程是已知了，如果直接能得到反向過程，那整個模型就有了。然而，前向擴散核 的逆步驟 難以計算。那該怎么辦呢？定義一個網(wǎng)絡(luò)去學(xué)唄，也就是 。

反向擴散過程，即生成過程，是逆方向上的一個馬爾科夫鏈，其中每個隱變量 僅從前一個隱變量 生成。

同樣配上噪聲數(shù)據(jù)和圖像數(shù)據(jù)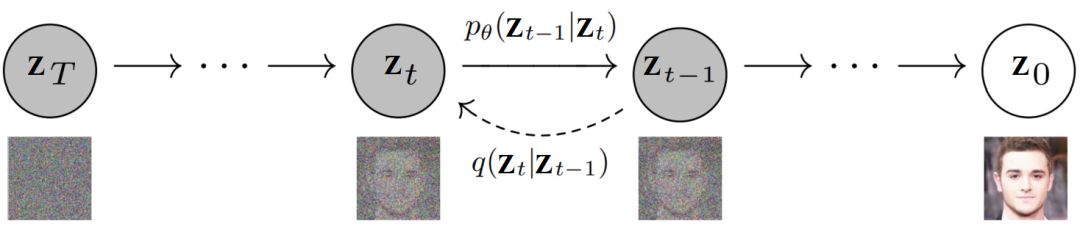， 上圖中，除了上文提到的前向擴散核 ，還有需要學(xué)習(xí)的反向擴散核（RDK），

• 它表示給定 后 的 PDF，其中 為逆過程涉及的分布的參數(shù)，我們使用神經(jīng)網(wǎng)絡(luò)來學(xué)習(xí)這些參數(shù)。

• 它是反向擴散過程中每一步用到的“轉(zhuǎn)移函數(shù)”。

我們知道，最終的隱變量的分布 是標準高斯分布。然后我們可以更新馬爾可夫 HVAE 的聯(lián)合分布，而聯(lián)合分布為：

隨著時間步驟的推移，輸入數(shù)據(jù)被逐步加入噪聲，直到它變成純高斯噪聲；而擴散模型旨在學(xué)習(xí)反轉(zhuǎn)這個過程。一旦模型優(yōu)化好，采樣過程就像從 采樣高斯噪聲一樣簡單，然后迭代運行 個步驟的去噪轉(zhuǎn)換 ，以生成新的數(shù)據(jù) 。

? 損失函數(shù)

目標已經(jīng)知道了，就是學(xué)習(xí)一系列反向擴散核，現(xiàn)在就缺損失函數(shù)了。

下面，我們主要來看一下在 ELBO 的推導(dǎo)中的關(guān)鍵項。對于任意復(fù)雜的馬爾可夫 HVAE 中的任意后驗，涉及到的 KL 散度項

很難最小化，但在擴散模型中，可以利用高斯轉(zhuǎn)移這個假設(shè)來使優(yōu)化變得容易處理。

由前文可知，我們已經(jīng)推導(dǎo)出 的公式，當(dāng)然同時也有 的高斯形式。然后，我們可以將這些公式代入 的貝葉斯法則展開式中，并簡化為以下形式：

由此可見， 呈高斯分布，均值 是 和 的函數(shù)，方差 是系數(shù) 的函數(shù)。這些系數(shù) 是已知的并且在每個時間步都是固定的。根據(jù)上式，我們可以將方差重寫為 ，其中：

為了盡可能匹配近似去噪轉(zhuǎn)換步驟 和真實去噪轉(zhuǎn)換步驟 ，我們可以將其建模為高斯分布。此外，由于已知所有 項在每個時間步都被凍結(jié)，因此我們可以立即將近似去噪過渡步驟的方差構(gòu)造為 。然而，我們必須將其平均值 參數(shù)化為 的函數(shù)，因為 不以 為條件。

然后，利用兩個高斯分布之間的 KL 散度為：

在我們這里，可以將兩個高斯的方差設(shè)置為完全匹配，優(yōu)化 KL 散度項可以減少兩個分布均值之間的差異：

其中， 為 ， 為 。換句話說，我們想要優(yōu)化與 匹配的 ，從式 可以看出，其形式為：

由于 也以 為條件，因此我們可以通過將它設(shè)置為以下形式來匹配 ：

其中 由神經(jīng)網(wǎng)絡(luò)參數(shù)化，該神經(jīng)網(wǎng)絡(luò)試圖從加噪圖像 和時間步 中預(yù)測原始圖像 。

因此，優(yōu)化問題就簡化為：

因此，優(yōu)化模型歸結(jié)為學(xué)習(xí)神經(jīng)網(wǎng)絡(luò)去從任意加噪圖像中預(yù)測原始圖像。此外，最小化我們導(dǎo)出的 ELBO 目標在所有加噪水平上的求和項可以通過最小化所有時間步長的期望來近似：

然后可以在時間步長上隨機采樣的樣本進行優(yōu)化。

另外，最終的損失函數(shù)也可以為，

其中， 是一個神經(jīng)網(wǎng)絡(luò)，它學(xué)習(xí)預(yù)測源噪聲 ，從而確定 和 。根據(jù)經(jīng)驗，發(fā)現(xiàn)預(yù)測噪聲會帶來更好的性能。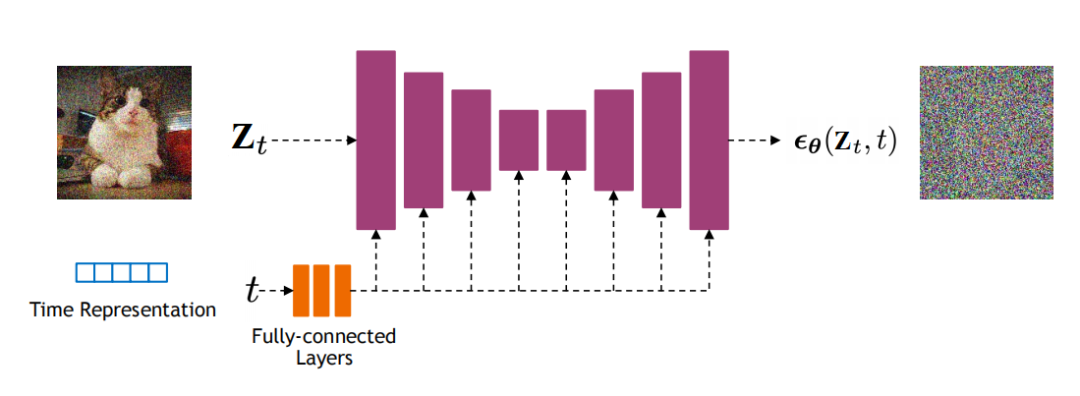

本篇到此告一段落，先對擴散模型有個大致概念，有關(guān)擴散模型的更多內(nèi)容將在后面陸續(xù)展開。