leetcode題解--訪問所有點的最小時間
這道題一到手,感覺高大上,第一反應(yīng)是覺得好難,其實是個典型的扮豬吃老虎的題目,找對方法就很簡單。
來!看題~
題目1266. 訪問所有點的最小時間
平面上有 n 個點,點的位置用整數(shù)坐標(biāo)表示 points[i] = [xi, yi] 。請你計算訪問所有這些點需要的 最小時間(以秒為單位)。
你需要按照下面的規(guī)則在平面上移動:
每一秒內(nèi),你可以:沿水平方向移動一個單位長度,或者 沿豎直方向移動一個單位長度,或者 跨過對角線移動 sqrt(2) 個單位長度(可以看作在一秒內(nèi)向水平和豎直方向各移動一個單位長度)。必須按照數(shù)組中出現(xiàn)的順序來訪問這些點。在訪問某個點時,可以經(jīng)過該點后面出現(xiàn)的點,但經(jīng)過的那些點不算作有效訪問。
示例 1:
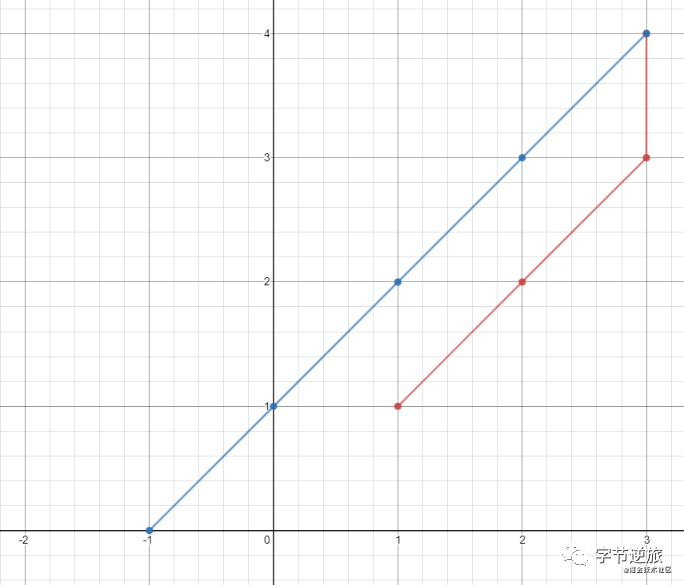
輸入:points = [[1,1],[3,4],[-1,0]]
輸出:7
解釋:一條最佳的訪問路徑是: [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
從 [1,1] 到 [3,4] 需要 3 秒
從 [3,4] 到 [-1,0] 需要 4 秒
一共需要 7 秒
示例 2:
輸入:points = [[3,2],[-2,2]]
輸出:5
提示:
points.length == n 1 <= n <= 100 points[i].length == 2 -1000 <= points[i][0], points[i][1] <= 1000
題解:
我們來一步步吃掉它吧。
第一步
這道題的實際上是一道幾何數(shù)學(xué)題,正確解法的第一步是要先畫出直角坐標(biāo)系,給坐標(biāo)軸上所有坐標(biāo)點畫相對于坐標(biāo)軸的平行線,就會形成一個個小正方形,然后按示例標(biāo)好各點位置,自己試著走兩步,接著就能發(fā)現(xiàn)其中奧秘。
第二步
在最小正方形上,從一個點到另一個相臨點算一個時間單位,走最小正方形的對角線也是一個時間單位。兩個點在坐標(biāo)系上,總共只會有兩種位置關(guān)系:在一條線上(包括相同點)、在矩形對角線上,而對角線又分為正方形和長方形這兩種。
第三步
在一條線上,這個距離怎么算,從圖上看就是線段長度;從數(shù)學(xué)上算,就是差值的絕對值;在正方形對角線上,因為最小正方形對角線算一個單位長度,所以這個時間值也可以按邊長,也就是xy值任意一軸的差值絕對值;在長方形對角線上,這個時間值的算法可以先走一個長方形內(nèi)最大正方形,走完后就在一條線上了,再走剩下的直線;你會發(fā)現(xiàn),長方形內(nèi)最大正方形的邊長就是長方形最短邊長,所以走到對角線上的點可以總結(jié)為最長邊長;
第四步
經(jīng)過上面分析,走完兩點所有情況下的時間值,都可以總結(jié)為兩點間形成的長方形(一條線上可以假設(shè)一條邊為0)的最長邊長值。按這種思路走完所有的點,再把每一段加起來就能得到最終結(jié)果了。
最后,上答案:
var minTimeToVisitAllPoints = function(points) {
let res = 0
for(let i = 0; i < points.length-1; i++){
let next = points[i + 1]
let cur = points[i]
let diff = Math.max(Math.abs(cur[0] - next[0]), Math.abs(cur[1] - next[1]))
res += diff
}
return res
}
這個解法還可以再優(yōu)化下,每次循環(huán)少了一步points的長度-1的計算,能節(jié)省點時間
var minTimeToVisitAllPoints = function(points) {
let res = 0
for(let i = 1; i < points.length; i++){
let last = points[i - 1]
let cur = points[i]
let diff = Math.max(Math.abs(cur[0] - last[0]), Math.abs(cur[1] - last[1]))
res += diff
}
return res
}
復(fù)雜度
時間復(fù)雜度O(n),其中 NN 是數(shù)組的長度。; 空間復(fù)雜度O(1);
題目鏈接:https://leetcode-cn.com/problems/minimum-time-visiting-all-points
推薦作者更多原創(chuàng):
