計(jì)算機(jī)起源的數(shù)學(xué)思想


萊布尼茨之夢(mèng)
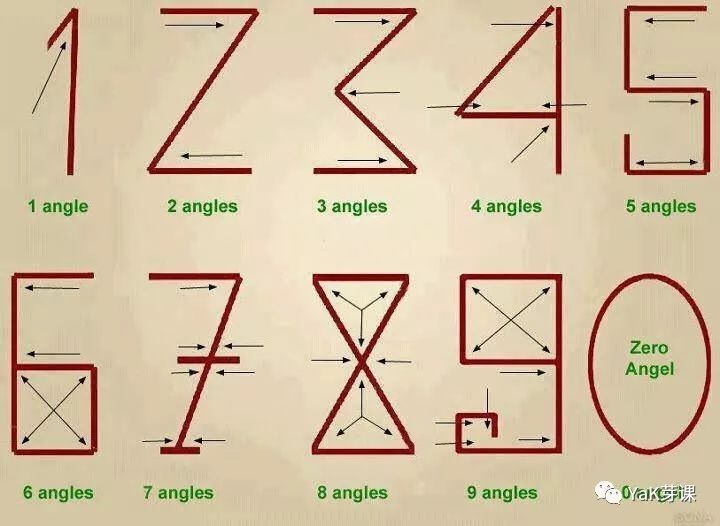
布爾的邏輯代數(shù)

現(xiàn)在我們以邏輯代數(shù)的觀點(diǎn)看這個(gè)式子,它體現(xiàn)了這樣一個(gè)含義:沒有任何東西可以同時(shí)屬于又不屬于某個(gè)類。這點(diǎn)讓布爾十分振奮,因?yàn)檫@剛好體現(xiàn)了亞里士多德的排中律,這就使他確信自己找對(duì)了路子。
所有y都是z y=yz
------------ ?
所有x都是z x=xz
x=xy
y=yz => x = xy = x(yz) = (xy)z = xz

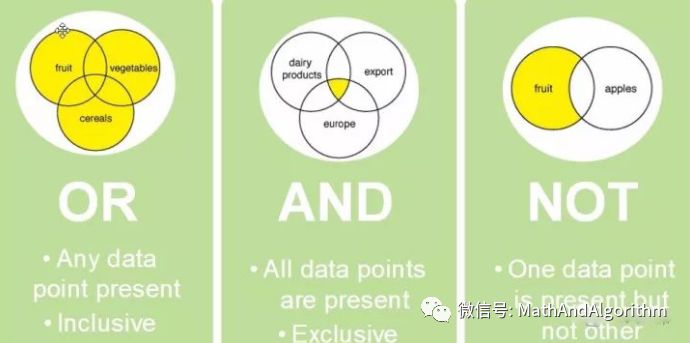
今天的布爾代數(shù)
AND | 1 0 ----------------------- 1 | 1 0 0 | 0 0
OR | 1 0 ----------------------- 1 | 1 1 0 | 1 0
NOT | -------------- 1 | 0 0 | 1

弗雷格的突破與絕望

康托爾,對(duì)無限的探索

大衛(wèi)希爾伯特

哥德爾完備性定理
U說某個(gè)特殊命題在PM中不可證。
那個(gè)特殊的命題就是U本身。
因此,U說"U在PM中不可證"
圖靈和圖靈機(jī)
找到一種算法,判定一個(gè)給定的自然數(shù)是否屬于集合D。
—THE END—
評(píng)論
圖片
表情
