Apple官網(wǎng)源碼中使用transform:matrix(),這是什么?
開篇
01
向量與矩陣基礎(chǔ)知識
關(guān)于這部分內(nèi)容,有線性代數(shù)基礎(chǔ)的同學(xué)們可以忽略本部分內(nèi)容,在這里筆者只會介紹最基礎(chǔ)的內(nèi)容,主要涉及什么是向量和矩陣,以及對應(yīng)的基礎(chǔ)運算。
向量
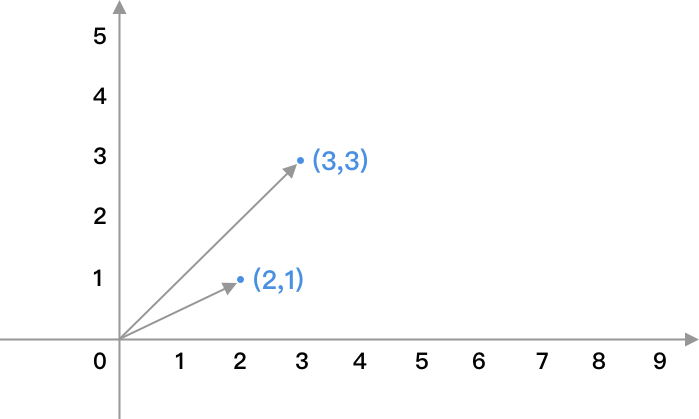
向量被用于許多科學(xué)領(lǐng)域用來描述方向和大小,我們一般用笛卡爾坐標(biāo)系進行向量的描述,向量簡單的來說就是把數(shù)排成一列或一行進行展示,比如向量(2,1)和(3,3)在坐標(biāo)系中表示如下:
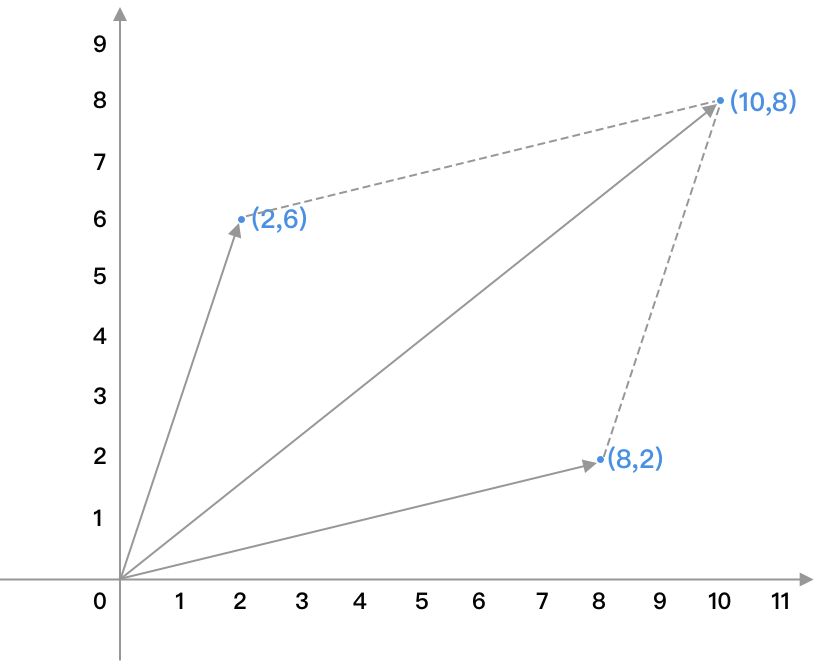
假設(shè)我們現(xiàn)在有兩個向量AB(8,2)和向量AC(2,6),我們對其進行加、減、乘運算,示例如下:
向量加法:
AB+AC=AD
(8,2)+(2,6)=(8+2,2+6)=(10,8)
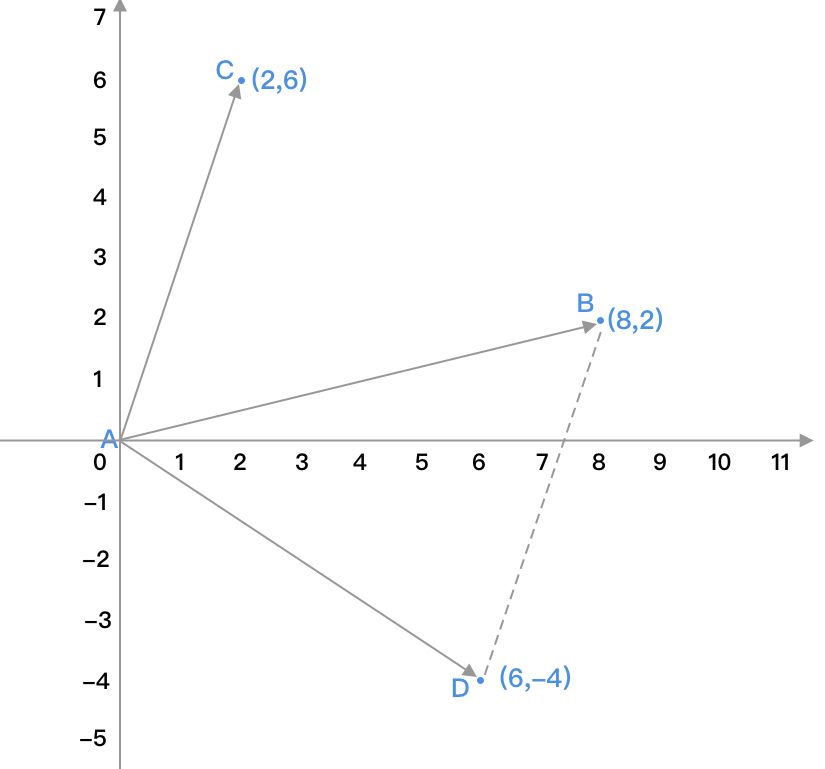
向量減法:
AB-AC= AD
(8,2)-(2,6)=(8-2,2-6)=(6,-4)
向量乘法:
AB??AC = AD
(8,2)??(2,6)=(8??2,2??6)=(16,12)
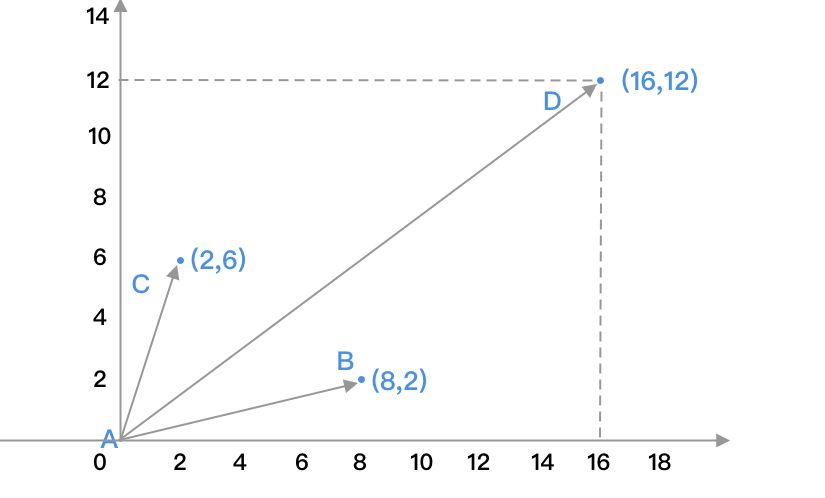
從上述例子我們可以看出,向量的運算即為每個向量對應(yīng)的位置進行兩兩相加、兩兩相減或兩兩相乘。
矩陣
簡單來說把數(shù)排列成長方形就是矩陣,我們一般用幾行幾列來描述矩陣,比如 2??2 矩陣,2??3 矩陣等,乘號左邊代表行數(shù),乘號右邊代表列數(shù),如下圖所示表示2??2 的矩陣:
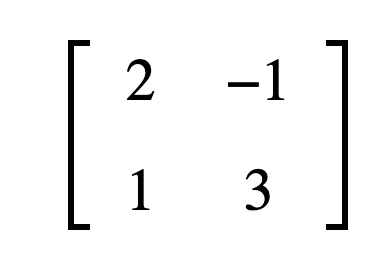
矩陣相加:
相同規(guī)模(行數(shù)列數(shù)都相等)的矩陣之間的加法如下圖所示:
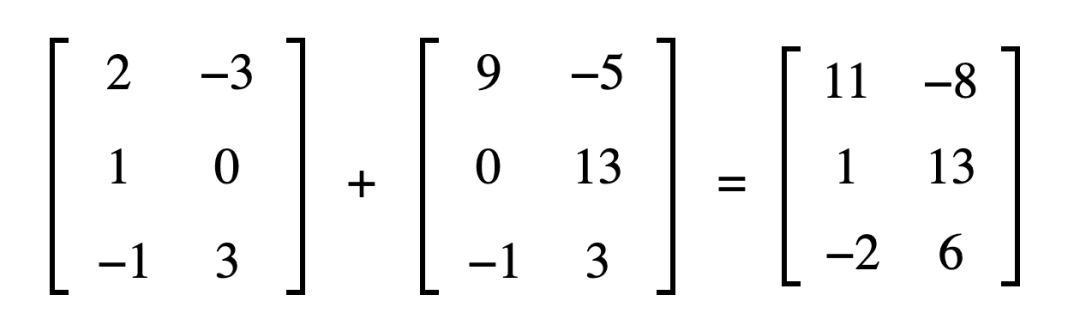
我們可以看出是對應(yīng)的位置兩兩相加而得。
矩陣相乘
1、矩陣與向量相乘,示意圖如下:
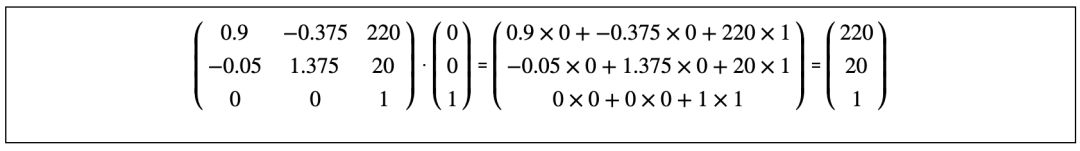
從圖可以看出矩陣與向量相乘結(jié)果為向量,矩陣每行的數(shù)字分別與向量每行對應(yīng)的位置分別相乘最后將結(jié)果相加,得到結(jié)果向量。
2、矩陣與矩陣相乘
比如 2??4 的矩陣與 4???3 的矩陣相乘我們得到一個 2??3 的矩陣,如下圖所示:
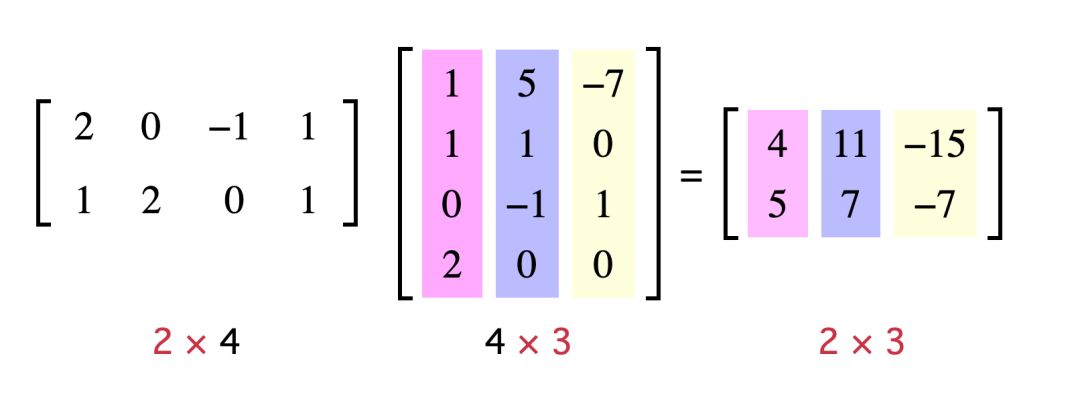
從圖示中我們可以看出,我們左邊矩陣的每行與右邊矩陣的每列分別相乘,相乘規(guī)則如矩陣與向量相乘的規(guī)則一樣,最終得到矩陣的行數(shù)等于左邊矩陣的行數(shù),列數(shù)等于右邊矩陣的列數(shù)。
02
一個matrix()的例子
介紹完基本向量和矩陣的知識后,我們來看看一個matrix()的例子,transform:matrix(a,b,c,d,ex,fy)一共六個參數(shù),用矩陣表示如下圖所示:

注:參數(shù)書寫的方向是豎著寫的。
這六個參數(shù)代表什么意思,這里先不做介紹,稍后會詳細(xì)介紹,現(xiàn)在我們有這樣一個元素,其對應(yīng)的CSS屬性如下:
#transformedObject {
position: absolute;
left: 0px;
top: 0px;
width: 200px;
height: 80px;
}
此段代碼,對應(yīng)的頁面效果如下:
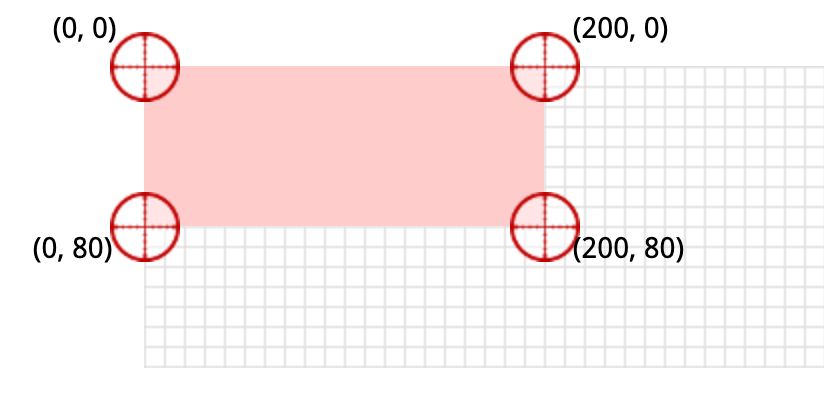
從上圖我們可以看出,此長方形的四個頂點從左頂點開始,順時針方向?qū)?yīng)的坐標(biāo)分別為:(0,0)、(200,0)、(200,80)、(0,80),我們對其進行transform:matrix(0.9, -0.05, -0.375, 1.375, 220, 20)變換,css代碼如下:
#transformedObject {
position: absolute;
left: 0px;
top: 0px;
width: 200px;
height: 80px;
transform: matrix(0.9, -0.05, -0.375, 1.375, 220, 20);
transform-origin: 0 0;
}
注:transform-origin是變形原點,也就是該元素圍繞著那個點變形或旋轉(zhuǎn),該屬性只有在設(shè)置了transform-origin屬性的時候起作用。
應(yīng)用這個屬性后的效果如下圖:
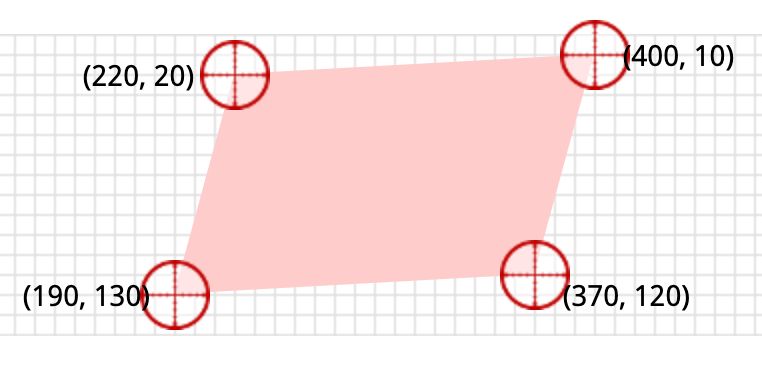
好奇的你,你一定困惑這四個點的值是怎么得出來的呢,其實有了前面的向量和矩陣知識,我們很容易算出,matrix(0.9, -0.05, -0.375, 1.375, 220, 20)用矩陣表示如下圖所示:
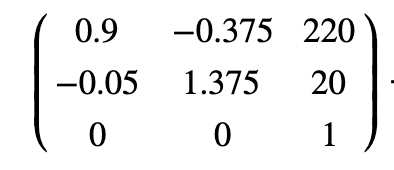
元素最初的每個頂點相當(dāng)一個向量,例如(200,0)可用下圖表示:
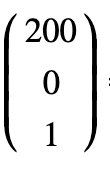
變換后的四個點的坐標(biāo)值,其實是matrix(0.9, -0.05, -0.375, 1.375, 220, 20)對應(yīng)的矩陣與原始四個點對應(yīng)的向量分別相乘而得,具體的運算過程如下圖:
與(200, 80)相乘的運算過程得到點(370,120):

與(200, 0)相乘的運算過程得到點(400,10):
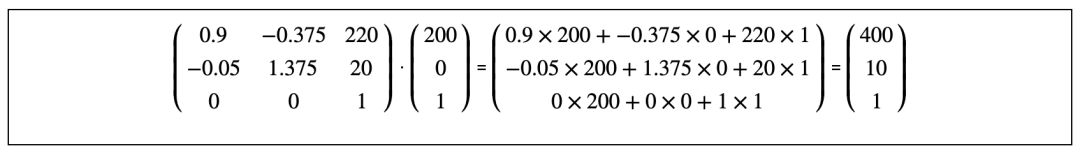
與(0, 80)相乘的運算過程得到點(190,130):
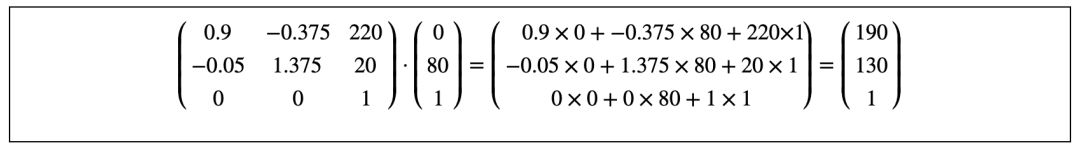
與(0,0)相乘的運算過程得到點(220,20):
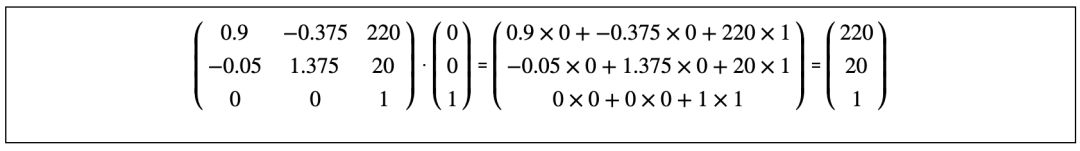
經(jīng)過運算后,我們得到最終變換后的四個頂點坐標(biāo): (220,20),(400,10),(370,120),(190,130)
03
matrix參數(shù)詳細(xì)介紹
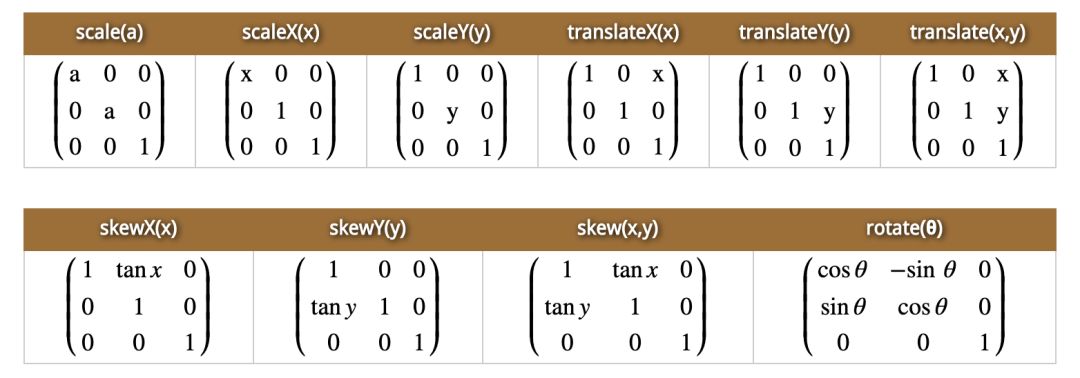
通過前面的學(xué)習(xí),我們學(xué)到了向量和矩陣的基礎(chǔ)知識,一個matrix()變換的例子,我們通過矩陣運算算出了變換后的結(jié)果。接下來我們一起學(xué)習(xí)下transform:matrix(a,b,c,d,tx,ty)這六個參數(shù)代表的意義,其實這六個參數(shù),對應(yīng)的是translate(x,y),scale(x,y),rotate(angle),skew(x-angle,y-angle)這些效果,每種變換效果對應(yīng)的參數(shù)不同,如下圖總結(jié):
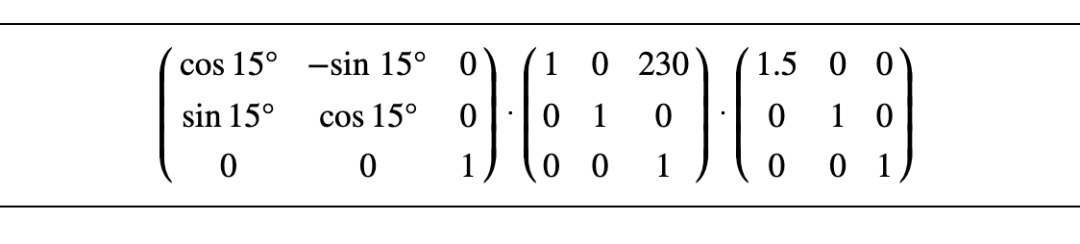
現(xiàn)在有這個需求,我們對元素進行順時針旋轉(zhuǎn)15度,X軸方向右移230px, X軸方向擴大1.5倍,我們使用基本的變換屬性代碼如下:
#o1 {
transform-origin: 0px 0px;
transform: rotate(15deg) translateX(230px) scaleX(1.5);
}
如果用transform:matrix()怎么實現(xiàn)如上的相同效果呢,其實我們可以利用transform:matrix(a,b,c,d,tx,ty)這六個參數(shù)對應(yīng)的總結(jié)(如上圖),其實就是每種變換對應(yīng)的矩陣參數(shù)相乘的結(jié)果得到這6個參數(shù)值,記住一定要按照rotate,translateX,scaleX對應(yīng)的順序進行舉行相乘(矩陣相乘順序不同結(jié)果不同),如下圖所示:(運算的結(jié)果筆者就不寫了,留給大家練習(xí)下矩陣相乘)

今天的內(nèi)容就介紹到這里,我們理解了transform這個高級屬性——matrix()矩陣屬性,通過這個屬性我們了解其背后的數(shù)學(xué)邏輯,只有理解掌握這個屬性后,我們才能實現(xiàn)更為復(fù)雜的動畫效果。

點擊上方卡片,關(guān)注一下~